c语言(转义字符)
前言:
内容:
然后记一下转义字符
\? 在书写连续多个问号时使用,防止他们被解析成三字母词
\' 用于表示字符常量'
\\ 用于表示一个反斜杠,防止他被解析为一个转义序列符
\n 换行
\r 回车
\t 水平制表符
\ddd ddd表示1~3个八进制数字。如:\130 X
\xdd dd表示2个十六进制数字。如:\x30 0
#include <stdio.h>
//int main()
//{
// printf("abc\0defg");
// return 0;
// } //%c - 打印字符
//%s - 打印字符串
//int main()
//{
// printf("%s\n","(are you ok ??)");
// return 0;
//}//int main()
//{
// printf("%c\n", '\'');
// return 0;
// } //int main()
//{
// printf("abc\ndefg");
// return 0;
//}
//
//
//8进制 130
//10进制 8*8 8*3 0*8*0
//
//10进制 88
//
//8进制 62
//10进制 6*8+2*8 0
//48+2=
//
//int main()
{printf("%c\n",'\130');return 0;} //%d - 打印整型
//%c - 打印字符
//%s - 打印字符串
//%f - 打印float类型的数据
//%1f - 打印double类型的数据
相关文章:
)
c语言(转义字符)
前言: 内容: 然后记一下转义字符 \? 在书写连续多个问号时使用,防止他们被解析成三字母词 \ 用于表示字符常量 \\ 用于表示一个反斜杠,防止他被解析为一个转义序列符 \n 换行 \r …...

easyexcel读取写入excel easyexceldemo
1.新建springboot项目 2.添加pom依赖 <name>excel</name> <description>excelspringboot例子</description><parent> <groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-parent</artifactId&…...
与主成分分析(PCA)在数据降维与特征提取中的应用)
【人工智能数学基础篇】——深入详解矩阵分解:奇异值分解(SVD)与主成分分析(PCA)在数据降维与特征提取中的应用
目录 1. 引言 2. 矩阵分解概述 2.1 矩阵分解的意义 3. 奇异值分解(SVD) 3.1 定义与数学基础 3.2 SVD 的性质 3.3 SVD 在数据降维中的应用 3.4 示例代码:使用 SVD 进行图像压缩 3.5 结果分析 4. 主成分分析(PCA࿰…...

ThreeJS示例教程200+【目录】
Three.js 是一个强大的 JavaScript 库,旨在简化在网页上创建和展示3D图形的过程。它基于 WebGL 技术,但提供了比直接使用 WebGL 更易于使用的API,使得开发者无需深入了解 WebGL 的复杂细节就能创建出高质量的3D内容。 由于目前内容还不多,下面的内容暂时做一个占位。 文章目…...

DC-DC稳压电源——实战(基于Ti5450芯片)基础知识篇(1)
一:基础知识-耦合 1)去耦电容 (1)耦合与去耦 耦合:系统内部的各个部分之间存在相互依赖、相互影响、相互制约的情况。用人话说就是不同部分之间的相互影响。 去耦:自然就是消除不同部分之间的影响了。 &…...

pyrender 渲染mesh
目录 render_meshes函数 调用函数 render_meshes函数 def overlay_human_meshes(humans, K, model, img_pil, unique_colorFalse):# Color of humans seen in the image._color [color[0] for _ in range(len(humans))] if unique_color else color# Get focal and princpt …...

防火墙安全策略
目录 一.拓扑信息 二.需求分析 三.命令行详细配置信息 1.配置IP 2.交换机配置 3.修改安全区域 4.安全策略 四.web界面详细配置 1.配置IP和设置安全区域 2.交换机配置 3.安全策略 五.测试 一.拓扑信息 二.需求分析 1.VLAN 2属于办公区域;VLAN 3属于生…...
方法清除文本框内容)
selenium clear()方法清除文本框内容
在使用Selenium进行Web自动化测试时,清除文本框内容是一个常见的需求。这可以通过多种方式实现,取决于你使用的是哪种编程语言(如Python、Java等)以及你的具体需求。以下是一些常见的方法: 1. 使用clear()方法 clear…...

(回溯分割)leetcode93 复原IP地址
#include<iostream> #include<vector> #include<string> #include<algorithm> using namespace std; //卡尔的图不是按照程序执行过程而是直接画程序会执行的过程 // 实际执行是:n个字符,递推n1后(叶子节点ÿ…...

高性能队列 Disruptor 在 IM 系统中的实战
高性能队列 Disruptor 在 IM 系统中的实战 前三期我们介绍了Disruptor的典型使用场景和相关高性能原理,本期我介绍一下Disruptor在IM系统用的应用实战,IM系统即社交聊天系统,对实时性的要求非常高,非常符合Disruptor的使用场景。 …...

原生HTML集合
一、表格 1、固定表格 <div class"tablebox"><div class"table-container"><table id"myTable" border"0" cellspacing"0" cellpadding"0"><thead><tr></tr></thead>…...

ES6 简单练习笔记--变量申明
一、ES5 变量定义 1.在全局作用域中 this 其实就是window对象 <script>console.log(window this) </script>输出结果: true 2.在全局作用域中用var定义一个变量其实就相当于在window上定义了一个属性 例如: var name "孙悟空" 其实就相当于执行了 win…...

2025.1.21——六、BUU XSS COURSE 1
题目来源:buuctf BUU XSS COURSE 1 一、打开靶机,整理信息 有吐槽和登陆两个尝试点,题目名称提示是XSS漏洞 XSS(Cross-Site Scripting)漏洞 1.定义:跨站脚本攻击,是一种常见的 Web 安全漏洞。攻…...

Linux - 五种常见I/O模型
I/O操作 (输入/输出操作, Input/Output) 是指计算机与外部设备就行数据交互的过程. 什么是外部设备: 如键盘, 鼠标, 硬盘, 网卡等. 五种常见的 I/O 模型: 阻塞 I/O非阻塞 I/O信号驱动 I/OI/O 多路复用异步 I/O 阻塞 I/O 阻塞 I/O 的特点: 当用户发起 I/O 请求后, 进程/线程就…...
【负载均衡式在线OJ】加载题目信息(文件版)
目录 如何读取文件 -- 常见流程 代码 如何读取文件 -- 常见流程 在C中使用 std::ifstream来打开文件流是一个常见的操作,用于创建一个输入文件流,并尝试打开名为 question_list的文件。if (!in.is_open()):检查文件是否成功打开。如果文件未…...

“上门按摩” 小程序开发项目:基于 SOP 的全流程管理
在竞争激烈的生活服务市场,“上门按摩” 服务需求日益增长。为满足这一需求,我们启动了 O2O 模式的 “上门按摩” 小程序开发项目,该项目涵盖客户端、系统管理端、技师端。以下将通过各类 SOP 对项目进行全面管理,确保项目顺利推进。 一、项目启动 SOP:5W2H 分析法 What(…...
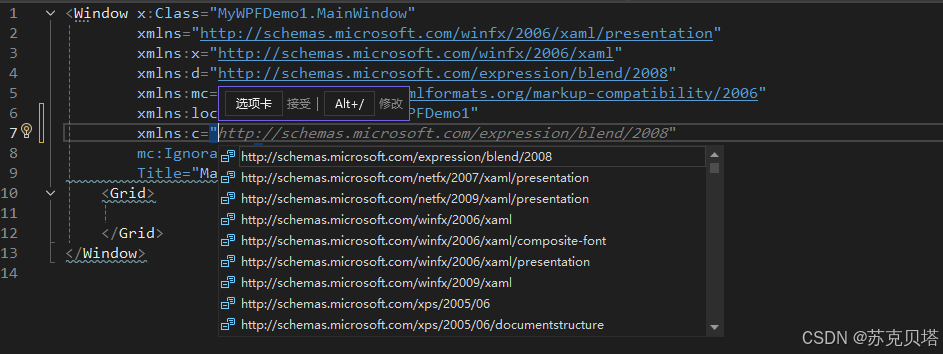
WPF1-从最简单的xaml开始
1. 最简单的WPF应用 1.1. App.config1.2. App.xaml 和 App.xaml.cs1.3. MainWindow.xaml 和 MainWindow.xaml.cs 2. 正式开始分析 2.1. 声明即定义2.2. 命名空间 2.2.1. xaml的Property和Attribute2.2.2. xaml中命名空间2.2.3. partial关键字 学习WPF,肯定要先学…...

2025牛客寒假算法营2
A题 知识点:模拟 打卡。检查给定的七个整数是否仅包含 1,2,3,5,6 即可。为了便于书写,我们可以反过来,检查这七个整数是否不为 4 和 7。 时间 O(1);空间 O(1)。 #include <bits/stdc.h> using namespace std;signed main()…...

编译Android平台使用的FFmpeg库
目录 前言 一、编译环境 二、搭建环境 1.安装MSYS2 2.更新系统包 2.1 打开MSYS2 MinGW 64-bit终端(mingw64.exe) 2.2 更新所有软件包到最新版本 2.3 安装必要的工具和库。 3. 克隆FFmpeg源码 4. 配置编译选项 5. 执行编译 总结 前言 记录学习…...

【C++高并发服务器WebServer】-2:exec函数簇、进程控制
本文目录 一、exec函数簇介绍二、exec函数簇 一、exec函数簇介绍 exec 函数族的作用是根据指定的文件名找到可执行文件,并用它来取代调用进程的内容,换句话说,就是在调用进程内部执行一个可执行文件。 exec函数族的函数执行成功后不会返回&…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

毫米波雷达基础理论(3D+4D)
3D、4D毫米波雷达基础知识及厂商选型 PreView : https://mp.weixin.qq.com/s/bQkju4r6med7I3TBGJI_bQ 1. FMCW毫米波雷达基础知识 主要参考博文: 一文入门汽车毫米波雷达基本原理 :https://mp.weixin.qq.com/s/_EN7A5lKcz2Eh8dLnjE19w 毫米波雷达基础…...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...
