二叉树的所有路径(力扣257)
因为题目要求路径是从上到下的,所以最好采用前序遍历。这样可以保证按从上到下的顺序将节点的值存入一个路径数组中。另外,此题还有一个难点就是如何求得所有路径。为了解决这个问题,我们需要用到回溯。回溯和递归不分家,每递归一次,我们就回溯一次,这样就能保证回到原来的位置,进而递归我们没有走过的节点,得到新的路径。大体思路就是这样,大家可以结合我的代码以及注释理解这道题目。另外,如果大家的二叉树遍历还不熟悉的话,最好先去看一下我的关于二叉树遍历的博客,再来看这道题,否则肯定会比较懵逼。
代码及注释如下:
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:
//参数有三个,一个为工作指针,一个为记录路径的数组,一个为储存最后结果的字符串数组
//注意千万不要将返回值设置为字符串数组,因为我们不需要每次递归都返回字符串,这跟之前每次递归返回数值不一样,我们这里将存储结果的容器放在参数引用就可以了void travel(TreeNode* cur,vector<int>& path,vector<string>& result){//这种记录路径的题目的递归终止条件不是遍历到空节点,而是遍历到叶子结点//为了确保将叶子结点也存入路径数组,需要在终止条件之前就push,否则会遗漏path.push_back(cur -> val);//处理逻辑(中)//终止条件:遍历到叶子节点if(cur -> left == NULL && cur -> right == NULL){//将数字转化为题目所规定的字符串string spath;for(int i = 0;i < path.size() - 1;i++){spath += to_string(path[i]);spath += "->";}spath += to_string(path[path.size() - 1]);result.push_back(spath);return;}if (cur->left) { //递归左孩子 travel(cur->left, path, result);path.pop_back(); // 回溯}if (cur->right) { // 递归右孩子travel(cur->right, path, result);path.pop_back(); // 回溯}}vector<string> binaryTreePaths(TreeNode* root) {vector<int> path;vector<string> result;if(root == NULL) return result;travel(root,path,result);return result;}
};相关文章:
)
二叉树的所有路径(力扣257)
因为题目要求路径是从上到下的,所以最好采用前序遍历。这样可以保证按从上到下的顺序将节点的值存入一个路径数组中。另外,此题还有一个难点就是如何求得所有路径。为了解决这个问题,我们需要用到回溯。回溯和递归不分家,每递归一…...
缓存)
Python OrderedDict 实现 Least Recently used(LRU)缓存
OrderedDict 实现 Least Recently used(LRU)缓存 引言正文 引言 LRU 缓存是一种缓存替换策略,当缓存空间不足时,会移除最久未使用的数据以腾出空间存放新的数据。LRU 缓存的特点: 有限容量:缓存拥有固定的…...

LabVIEW项目中的工控机与普通电脑选择
工控机(Industrial PC)与普通电脑在硬件设计、性能要求、稳定性、环境适应性等方面存在显著差异。了解这些区别对于在LabVIEW项目中选择合适的硬件至关重要。下面将详细分析这两种设备的主要差异,并为LabVIEW项目中的选择提供指导。 硬件设…...

Ansys Speos | Speos Meshing 网格最佳实践
概述 网格划分是在各种计算应用中处理3D几何的基本步骤: 表面和体积:网格允许通过将复杂的表面和体积分解成更简单的几何元素(如三角形、四边形、四面体或六面体)来表示复杂的表面和体积。 模拟和渲染:网格是创建离散…...

elasticsearch segment数量对读写性能的影响
index.merge.policy.segments_per_tier 是一个配置选项,用于控制 Elasticsearch 中段(segment)合并策略的行为。它定义了在每一层的段合并过程中,允许存在的最大段数量。调整这个参数可以优化索引性能和资源使用。 假设你有一个索…...

全同态加密理论、生态现状与未来展望(中2)
《全同态加密理论、生态现状与未来展望》系列由lynndell2010gmail.com和mutourend2010gmail.com整理原创发布,分为上中下三个系列: 全同态加密理论、生态现状与未来展望(上):专注于介绍全同态加密理论知识。全同态加密…...
鸿蒙UI(ArkUI-方舟UI框架)-开发布局
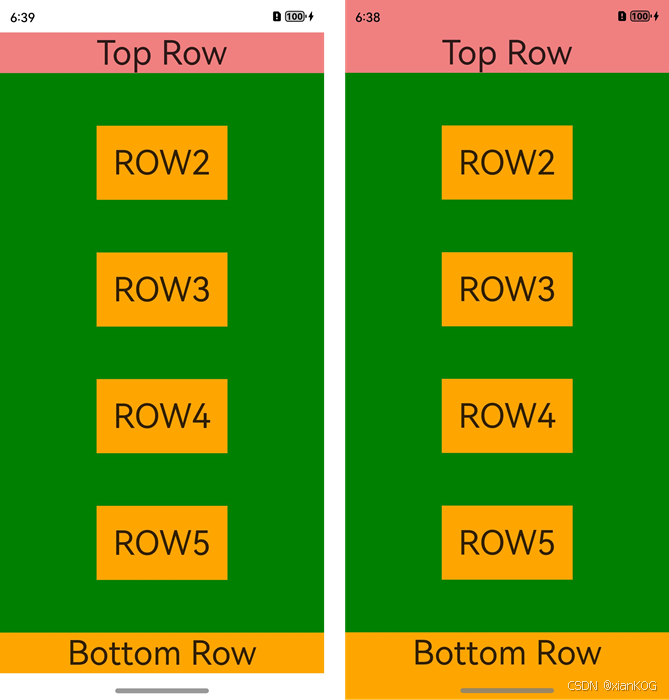
返回主章节 → 鸿蒙UI(ArkUI-方舟UI框架) 开发布局 1、布局概述 1)布局结构 2)布局元素组成 3)如何选择布局 声明式UI提供了以下10种常见布局,开发者可根据实际应用场景选择合适的布局进行页面开发。 …...
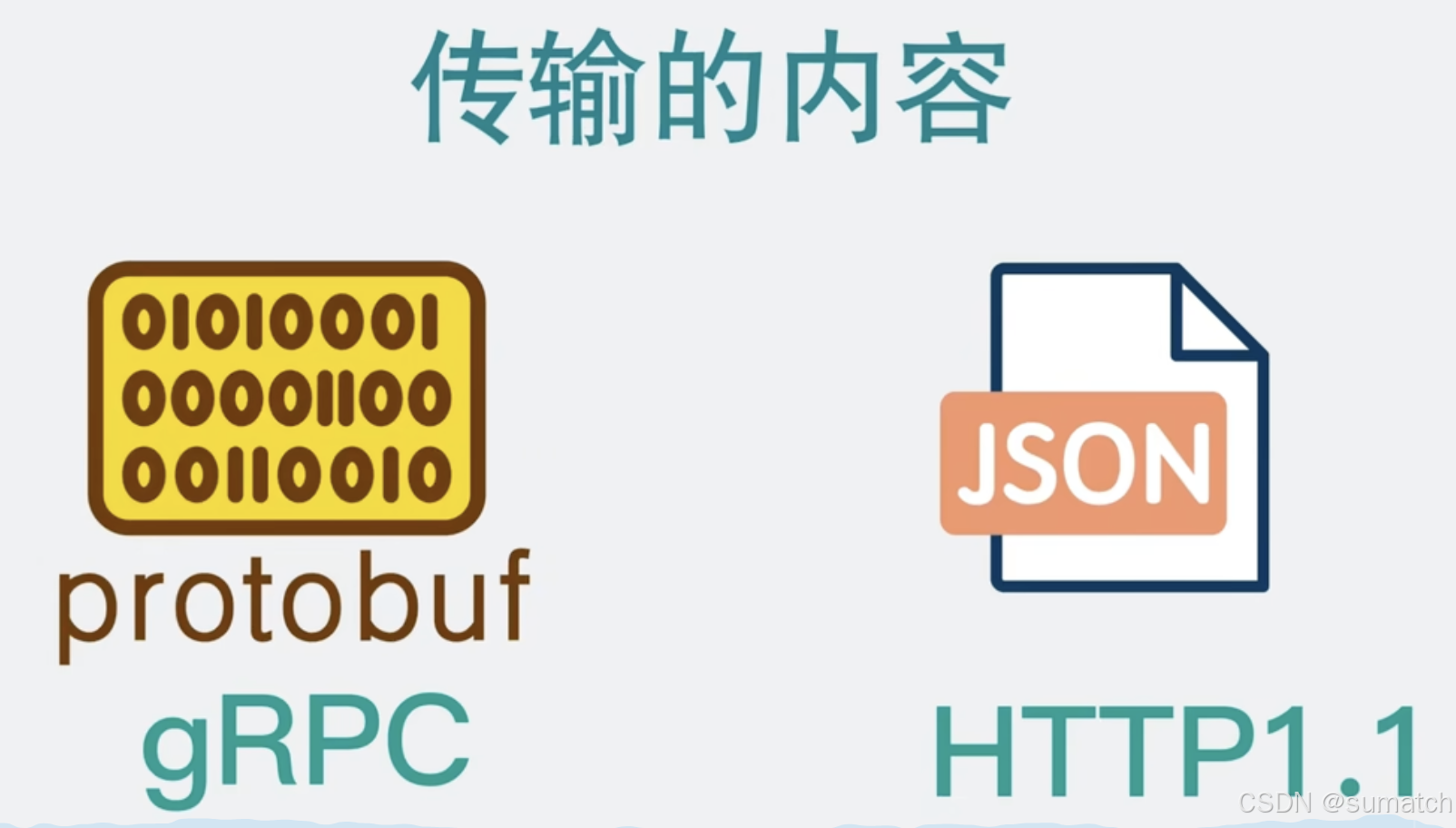
RPC是什么?和HTTP区别?
RPC 是什么?HTTP 是什么? 作为一个程序员,假设我们需要从A电脑的进程发送一段数据到B电脑的进程,我们一般会在代码中使用 Socket 进行编程。 此时,可选性一般就是 TCP 和 UDP 二选一,由于 TCP 可靠、UDP 不…...

Linux C\C++编程-建立文件和内存映射
【图书推荐】《Linux C与C一线开发实践(第2版)》_linux c与c一线开发实践pdf-CSDN博客 《Linux C与C一线开发实践(第2版)(Linux技术丛书)》(朱文伟,李建英)【摘要 书评 试读】- 京东图书 Linu…...
行政纠错——pycorrector学习
pycorrector是一个开源中文文本纠错工具,它支持对中文文本进行音似、形似和语法错误的纠正。此工具是使用Python3进行开发的,并整合了Kenlm、ConvSeq2Seq、BERT、MacBERT、ELECTRA、ERNIE、Transformer等多种模型来实现文本纠错功能。pycorrector官方仓库…...

Go的defer原理
Go 的 defer 原理 defer 是 Go 语言中的一个关键字,用于延迟执行一个函数调用。它通常用于处理资源释放、连接关闭等操作,确保这些操作在函数返回之前执行。 1. 什么是 defer? defer 关键字用于延迟执行一个函数调用,直到包含它…...

Windows 下本地 Docker RAGFlow 部署指南
Windows 下本地 Docker RAGFlow 部署指南 环境要求部署步骤1. 克隆代码仓库2. 配置 Docker 镜像加速(可选)3. 修改端口配置(可选)4. 启动服务5. 验证服务状态6. 访问服务7. 登录系统8. 配置模型8.1 使用 Ollama 本地模型8.2 使用在线 API 服务9. 开始使用10. 常见问题处理端…...

专题三_穷举vs暴搜vs深搜vs回溯vs剪枝_全排列
dfs解决 全排列&子集 1.全排列 link:46. 全排列 - 力扣(LeetCode) 全局变量回溯 code class Solution { public:vector<vector<int>> ans;vector<int> cur;vector<bool> used;vector<vector<int>> permute…...

【IEEE Fellow 主讲报告| EI检索稳定】第五届机器学习与智能系统工程国际学术会议(MLISE 2025)
重要信息 会议时间地点:2025年6月13-15日 中国深圳 会议官网:http://mlise.org EI Compendex/Scopus稳定检索 会议简介 第五届机器学习与智能系统工程国际学术会议将于6月13-15日在中国深圳隆重召开。本次会议旨在搭建一个顶尖的学术交流平台…...

华为E9000刀箱服务器监控指标解读
美信监控易内置了数千种常见设备监测器,能够监测超过20万项指标。这些指标涵盖了从硬件设备到软件系统,从网络性能到安全状态等各个方面。如下基于美信监控易——IT基础监控模块,对华为E9000刀箱服务器部分监控指标进行解读。 一、华为E9000…...

【LC】2544. 交替数字和
题目描述: 给你一个正整数 n 。n 中的每一位数字都会按下述规则分配一个符号: 最高有效位 上的数字分配到 正 号。剩余每位上数字的符号都与其相邻数字相反。 返回所有数字及其对应符号的和。 示例 1: 输入:n 521 输出&…...
QT QTreeWidget控件 全面详解
本系列文章全面的介绍了QT中的57种控件的使用方法以及示例,包括 Button(PushButton、toolButton、radioButton、checkBox、commandLinkButton、buttonBox)、Layouts(verticalLayout、horizontalLayout、gridLayout、formLayout)、Spacers(verticalSpacer、horizontalSpacer)、…...
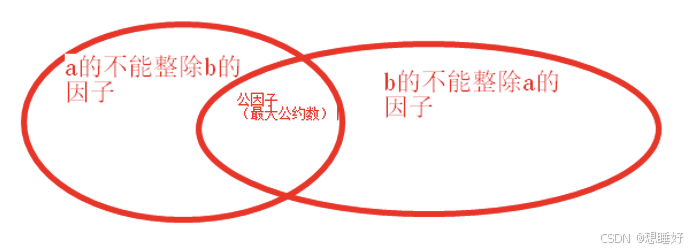
欧几里得算法求最小公倍数和最大公约数
一.最大公约数 gcd(a,b)gcd(b,a%b) 递归式,当且仅当b0,易得0和a的公约数为a.(可作为递归的出口) 证明: int gcd(int a, int b) {if (b 0) return a;else return gcd(b, a % b); } 二.最小公倍数 给定整数a b,求a b的最小公倍数 有图可知…...

Selenium配合Cookies实现网页免登录
文章目录 前言1 方案一:使用Chrome用户数据目录2 方案二:手动获取并保存Cookies,后续使用保存的Cookies3 注意事项 前言 在进行使用Selenium进行爬虫、网页自动化操作时,登录往往是一个必须解决的问题,但是Selenium每次…...
DeepSeek R1模型解读与使用
字节在春节前发布了doubao-1.5,它的官方介绍竟然是这样的: 这次发布了四个型号,doubao-1.5-pro-32k, doubao-1.5-pro-256k, doubao-1.5-lite-32k, doubao-1.5-vision-pro-32k,价格全部与上一个版本doubao模型一致,加量…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...
 error)
【前端异常】JavaScript错误处理:分析 Uncaught (in promise) error
在前端开发中,JavaScript 异常是不可避免的。随着现代前端应用越来越多地使用异步操作(如 Promise、async/await 等),开发者常常会遇到 Uncaught (in promise) error 错误。这个错误是由于未正确处理 Promise 的拒绝(r…...
