golang 使用双向链表作为container/heap的载体
MyHeap:container/heap的数据载体,需要实现以下方法:
Len:堆中数据个数
Less:第i个元素 是否必 第j个元素 值小
Swap:交换第i个元素和 第j个元素
Push:向堆中追加元素
Pop:从堆中取出元素
下面是使用双向链路作为数据载体的最小堆实现方式:
package mainimport ("container/heap""fmt"
)type HeapItem struct {Value intPrev *HeapItemNext *HeapItem
}type MyHeap struct {Head *HeapItemTail *HeapItemLength int
}func (h *MyHeap) Len() int {return h.Length
}func (h *MyHeap) Less(i, j int) bool {return h.Find(i).Value < h.Find(j).Value
}func (h *MyHeap) Swap(i, j int) {nodeI, nodeJ := h.Find(i), h.Find(j)isNear := h.IsNear(nodeI, nodeJ)// 记录I的前和后nodeIPrev, nodeINext := nodeI.Prev, nodeI.Next// 记录J的前和后nodeJPrev, nodeJNext := nodeJ.Prev, nodeJ.Next// 把J放到I的位置nodeIPrev.Next = nodeJnodeJ.Prev = nodeIPrevnodeJ.Next = nodeINext // near, 对于相邻元素, 这样操作有问题, 下面会重新赋值nodeINext.Prev = nodeJ // near, 对于相邻元素, 这样操作有问题, 下面会重新赋值// 把I放到J的位置nodeJPrev.Next = nodeI // near, 对于相邻元素, 这样操作有问题, 下面会重新赋值nodeI.Prev = nodeJPrev // near, 对于相邻元素, 这样操作有问题, 下面会重新赋值nodeI.Next = nodeJNextnodeJNext.Prev = nodeI// 对于相邻元素,重新赋值if isNear {nodeJ.Next = nodeInodeINext.Prev = nodeIPrevnodeJPrev.Next = nodeJNextnodeI.Prev = nodeJ}
}func (h *MyHeap) Push(v interface{}) {newItem := v.(*HeapItem)temp := h.Tail.Prevtemp.Next = newItemnewItem.Prev = tempnewItem.Next = h.Tailh.Tail.Prev = newItemh.Length++return
}func (h *MyHeap) Pop() interface{} {realTailNode := h.Tail.PrevrealTailNode.Prev.Next = realTailNode.NextrealTailNode.Next.Prev = realTailNode.Prevh.Length--return realTailNode
}func (h *MyHeap) IsNear(nodeI, nodeJ *HeapItem) bool {if nodeI.Next == nodeJ {return true}return false
}func (h *MyHeap) Find(i int) *HeapItem {nodeI := h.Headfor k := 0; k <= i; k++ {nodeI = nodeI.Next}return nodeI
}func (h *MyHeap) Show() {forward := ""backward := ""i := 0for curr := h.Head; curr != nil && i < 10; curr = curr.Next {forward += fmt.Sprintf("'%d'->", curr.Value)i++}j := 0for curr := h.Tail; curr != nil && j < 10; curr = curr.Prev {backward = fmt.Sprintf("'%d'<-", curr.Value) + backwardj++}fmt.Printf("forward=%s, backward=%s\n", forward, backward)
}func InitHeap() *MyHeap {head := &HeapItem{Value: -1}tail := &HeapItem{Value: -2}head.Next = tailtail.Prev = headreturn &MyHeap{Head: head,Tail: tail,Length: 0,}
}func main() {myHeap := InitHeap()heap.Init(myHeap)heap.Push(myHeap, &HeapItem{Value: 10})heap.Push(myHeap, &HeapItem{Value: 1000})heap.Push(myHeap, &HeapItem{Value: 5})heap.Push(myHeap, &HeapItem{Value: 1})heap.Push(myHeap, &HeapItem{Value: 7})myHeap.Show()for myHeap.Len() > 0 {item := heap.Pop(myHeap).(*HeapItem)fmt.Printf("%d ", item.Value)}fmt.Println()
}
相关文章:

golang 使用双向链表作为container/heap的载体
MyHeap:container/heap的数据载体,需要实现以下方法: Len:堆中数据个数 Less:第i个元素 是否必 第j个元素 值小 Swap:交换第i个元素和 第j个元素 Push:向堆中追加元素 Pop:从堆…...

C#集合操作优化:高效实现批量添加与删除
在C#中,对集合进行批量操作(如批量添加或删除元素)通常涉及使用集合类型提供的方法和特性,以及可能的循环或LINQ查询来高效地处理大量数据。以下是一些常见的方法和技巧: 批量添加元素 使用集合的AddRange方法&#x…...

142.WEB渗透测试-信息收集-小程序、app(13)
免责声明:内容仅供学习参考,请合法利用知识,禁止进行违法犯罪活动! 内容参考于: 易锦网校会员专享课 上一个内容:141.WEB渗透测试-信息收集-小程序、app(12) 软件用法,…...

24.日常算法
1. 数组中两元素的最大乘积 题目来源 给你一个整数数组 nums,请你选择数组的两个不同下标 i 和 j,使 (nums[i]-1)*(nums[j]-1) 取得最大值。请你计算并返回该式的最大值。 示例 1: 输入:nums [3,4,5,2] 输出:12 解释…...
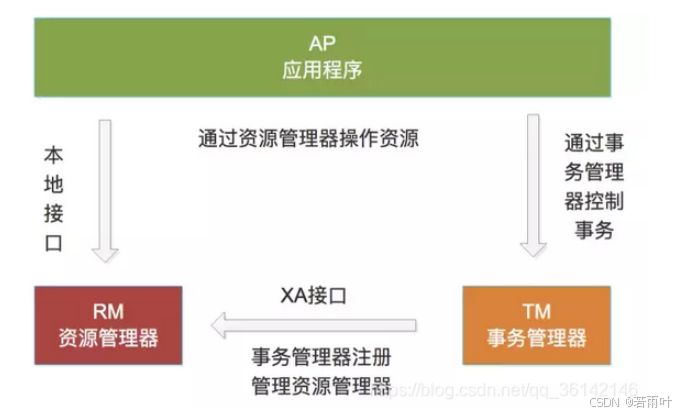
分布式理解
分布式 如何理解分布式 狭义的分布是指,指多台PC在地理位置上分布在不同的地方。 分布式系统 分布式系**统:**多个能独立运行的计算机(称为结点)组成。各个结点利用计算机网络进行信息传递,从而实现共同的“目标或者任…...

wordpress调用指定ID页面的链接
在WordPress中,如果你想调用一个指定ID的页面链接,可以使用以下几种方法: 方法一:使用页面ID 你可以直接使用页面的ID来生成链接。例如,如果你想链接到ID为123的页面,可以使用以下代码: <…...
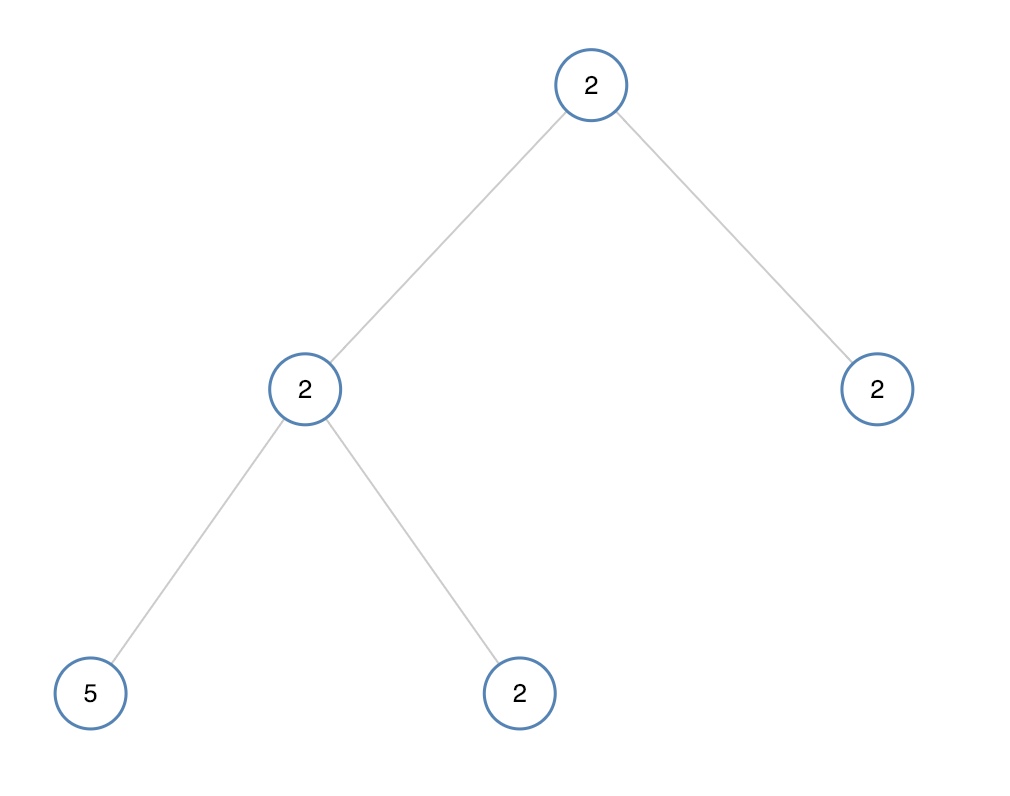
单值二叉树(C语言详解版)
一、摘要 今天要讲的是leetcode单值二叉树,这里用到的C语言,主要提供的是思路,大家看了我的思路之后可以点击链接自己试一下。 二、题目简介 如果二叉树每个节点都具有相同的值,那么该二叉树就是单值二叉树。 只有给定的树是单…...
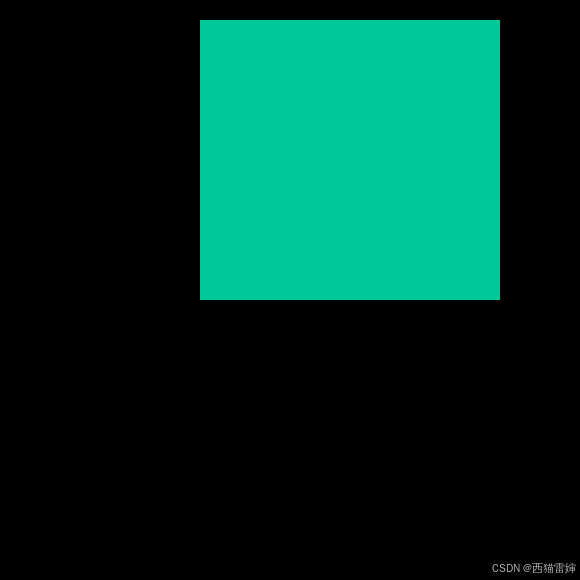
python学opencv|读取图像(四十二)使用cv2.add()函数实现多图像叠加
【1】引言 前序学习过程中,掌握了灰度图像和彩色图像的掩模操作: python学opencv|读取图像(九)用numpy创建黑白相间灰度图_numpy生成全黑图片-CSDN博客 python学opencv|读取图像(四十)掩模:三…...

速通Docker === Docker Compose
目录 Docker Compose 简介 Docker Compose 常用命令 使用 Docker Compose 启动 WordPress 普通启动方式(使用 Docker 命令) 使用 Docker Compose 启动 Docker Compose 的特性 Docker Compose 简介 Docker Compose 是一个用于定义和运行多容器 Dock…...
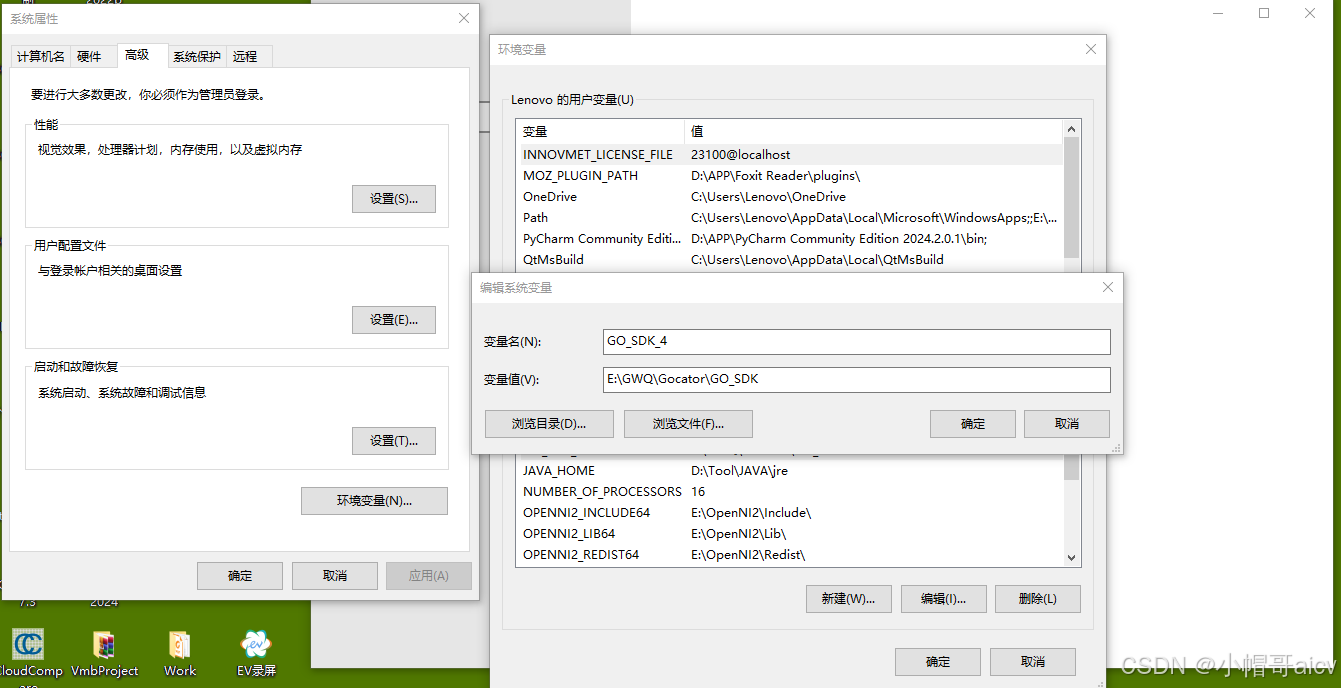
LMI Gocator GO_SDK VS2019引用配置
LMI SDK在VS2019中的引用是真的坑爹,总结一下经验,希望后来的人能少走弯路.大致内容如下: (1) 环境变量 (2)C/C 附加包含目录 E:\GWQ\Gocator\GO_SDK\Gocator\GoSdk E:\GWQ\Gocator\GO_SDK\Platform\kApi (3&#…...

技术之翼,创作之心
引言:初入编程的迷茫与追求 当我第一次接触到编程时,心中充满了既期待又迷茫的情感。那时,我还是一名刚刚踏入大学的学生,面对一门陌生而复杂的学科——计算机科学,我的内心充满了好奇与困惑。课堂上,老师…...

WebSocket异步导出
WebSocket异步导出 1、安装sockjs-client和stompjs2、连接后台3、vite.config.ts 配置反向代理4、导出并实时通信5、 封装WebSocket 文件注册登录(城通网盘) 1、安装sockjs-client和stompjs import SockJS from sockjs-client/dist/sockjs.min.js import Stomp from stompjs2、…...

OS2.【Linux】基本命令入门(1)
目录 1.操作系统是什么? 2.好操作系统的衡量标准 3.操作系统的核心工作 4.在计算机上所有行为都会被转换为硬件行为 5.文件 6.简单介绍一些基本命令 1.clear 2.pwd 3.ls 1.ls -l 2.隐藏文件的创建 3.ls -al 4.ls -ld 5.ls -F(注意是大写) 4.cd 1.cd .. "…...

【二叉树】4. 判断一颗二叉树是否是平衡二叉树。5. 对称二叉树。6. 二叉树的构建及遍历 7. 二叉树的分层遍历 。
判断一颗二叉树是否是平衡二叉树。OJ链接 可以在求树高度的过程中判断树是否平衡 对称二叉树。OJ链接 二叉树的构建及遍历。OJ链接 注意:public static int i最好把static去掉 否则当有多个测试用例时 i无法重新为0二叉树的分层遍历 。OJ链接 但此题要求返回List…...

OS Copilot功能测评:智能助手的炫彩魔法
简介: OS Copilot 是一款融合了人工智能技术的智能助手,专为Linux系统设计,旨在提升系统管理和运维效率。本文详细介绍了在阿里云ECS实例上安装和体验OS Copilot的过程,重点评测了其三个核心参数:-t(模式…...

MFC结构体数据文件读写实例
程序功能将结构体内数组数据写入文件和读出 2Dlg.h中代码: typedef struct Student {int nNum[1000];float fScore;CString sss;}stu; class CMy2Dlg : public CDialog { // Construction public:CMy2Dlg(CWnd* pParent NULL); // standard constructorstu stu1; ... } 2Dl…...

音频 PCM 格式 - raw data
文章目录 raw 音频格式:PCM其他音频格式:mp31. 无损压缩音频(类比 PNG 图像)2. 有损压缩音频(类比 JPEG 图像) 试了一下科大讯飞的音频识别云 api,踩了点坑 与本文无关:讯飞的 api 使…...

关于deepin上运行Qt开发的程序
国产化替代是将来各单位的主流趋势,探索自行开发应用程序在国产操作系统上正常运行是将来的主要工作之一。本文浅尝gui程序在统信社区版——deepin上遇到的小问题。 使用Qt在deepin上做了一个类似gif的帧动画弹窗,在编译运行时,程序可以正常…...

css 如何将字体进行压扁,即水平缩放scaleX
1、下面是来自baidu ai的结果: 2、下面是测试结果: .font-yh {text-align: center;font-family: msyh;display: inline-block; /* 确保transform作用于元素本身 */transform: scaleX(1.5); /* 水平缩放 */ } font-face {font-family: msyh;font-style:…...

C++AVL树(二)详解
文章目录 AVL树旋转单旋右单旋左单旋 双旋左右双旋右左双旋 平衡因子的更新左右双旋右左双旋 判断是不是AVL树时间复杂度分析全部的代码 AVL树 旋转 单旋 单旋是纯粹的一边高 单旋平衡因子是同号 右单旋 a,b,c自身不能发生旋转 并且也不能不向上继续更新(不能停…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...
