C++AVL树(二)详解
文章目录
- AVL树
- 旋转
- 单旋
- 右单旋
- 左单旋
- 双旋
- 左右双旋
- 右左双旋
- 平衡因子的更新
- 左右双旋
- 右左双旋
- 判断是不是AVL树
- 时间复杂度分析
- 全部的代码
AVL树
旋转
单旋
单旋是纯粹的一边高
单旋平衡因子是同号
右单旋
a,b,c自身不能发生旋转
并且也不能不向上继续更新(不能停止更新)



插入之前是h+2,插入后进行旋转后是h+2,没有对pParent它的子树的高度产生影响,不用继续向上更新
// 链接孩子和父亲
// 右单旋,旋转点是parent
void Rotate(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;// b可能为空树if (suLR != nullptr)subLR->_parent = parent;// 记录parent的parentpParent = parent->_parent;subL->_right = parent;parent->_parent = subL;// 1. 10是这棵树的总根if (parent == _root){subL = _root;subL->_parent = nullptr;}else{// 2. 10是这棵树的局部根// 就有父亲的父亲节点// pParent左可能是parent,右也可能是parentif (pParent->_left == parent){pParent->_left = subL;}else{pParent->_right = subL;}subL->_parent = pParent;}// 更新平衡因子subL->_bf = 0;parent->_bf = 0;}
左单旋
左单旋和右单旋类似

// 左单旋,旋转点是parent
void RotateL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;// b不是空树if (subRL)subRL->_parent = parent;// 记录父亲节点的父亲节点Node* pParent = parent->_parent;subR->_left = parent;parent->_parent = subR;// 1. 10是这棵树的总根if (_root == parent){_root = subR;subR->_parent = nullptr;}else{// 2. 10是这棵树的局部根if (pParent->_left == parent){pParent->_left = subR;}else{pParent->_right = subR;}subR->_parent = pParent;}subR->_bf = 0;parent->_bf = 0;
}
双旋
双旋平衡因子会异号
双旋是进行两次单旋
对于5来说右边高,对于10来说左边高,需要进行双旋
下面是进行的单旋解决不了问题

对于5来说右边高,对于10来说左边高,需要进行双旋
进行单旋解决不了问题,会变成下面的样子

左右双旋
h == 0

h == 1

右左双旋
右左双旋和左右双旋类似,这里就不画了
平衡因子的更新
左右双旋
双旋和单旋的平衡因子更新方式不同,双旋按照单旋的方式更新后5,10,8都是0,不符合逻辑
左右双旋中h0和h1具体场景分析,下面我们将a/b/c子树抽象为高度h的AVL
子树进行分析,另外我们需要把b子树的细节进一步展开为8和左子树高度为h-1的e和f子树,因为
我们要对b的父亲5为旋转点进行左单旋,左单旋需要动b树中的左子树。b子树中新增结点的位置
不同,平衡因子更新的细节也不同,通过观察8的平衡因子不同,这里我们要分三个场景讨论。
- 场景1:h >= 1时,新增结点插入在e子树,e子树高度从h-1并为h并不断更新8->5->10平衡因子,
引发旋转,其中8的平衡因子为-1,旋转后8和5平衡因子为0,10平衡因子为1。 - 场景2:h >= 1时,新增结点插入在f子树,f子树高度从h-1变为h并不断更新8->5->10平衡因子,引
发旋转,其中8的平衡因子为1,旋转后8和10平衡因子为0,5平衡因子为-1。 - 场景3:h == 0时,a/b/c都是空树,b自己就是一个新增结点,不断更新5->10平衡因子,引发旋转,其中8的平衡因子为0,旋转后8和10和5平衡因子均为0。

8的平衡因子会影响其它的平衡因子:
- 插入到8的左边,8的平衡因子为-1
- 插入到8的右边,8的平衡因子为1
- 8本身就是要插入的节点,8的平衡因子为0
// 左右双旋
void RotateLR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;// 提前存平衡因子int bf = subLR->_bf;RotateL(parent->_left);RotateR(parent);if (subLR->_bf == -1){subLR->_bf = 0;subL->_bf = 0;parent->_bf = 1;}else if (subLR->_bf == 1){subLR->_bf = 0;subL->_bf = -1;parent->_bf = 0;}else if (subLR->_bf == 0){subLR->_bf = 0;subL->_bf = 0;parent->_bf = 0;}else{assert(false);}
}
右左双旋
跟左右双旋类似,下面我们将a/b/c子树抽象为高度h的AVL子树进行分析,另外我们需要把b子树的细节进一步展开为12和左子树高度为h-1的e和f子树,因为我们要对b的父亲15为旋转点进行右单旋,右单旋需要动b树中的右子树。b子树中新增结点的位置不同,平衡因子更新的细节也不同,通过观察12的平衡因子不同,这里我们要分三个场景讨论。
- 场景1:h >= 1时,新增结点插入在e子树,e子树高度从h-1变为h并不断更新12->15->10平衡因子,引发旋转,其中12的平衡因子为-1,旋转后10和12平衡因子为0,15平衡因子为1。
- 场景2:h >= 1时,新增结点插入在f子树,f子树高度从h-1变为h并不断更新12->15->10平衡因子,引发旋转,其中12的平衡因子为1,旋转后15和12平衡因子为0,10平衡因子为-1。
- 场景3:h == 0时,a/b/c都是空树,b自己就是一个新增结点,不断更新15->10平衡因子,引发旋转,其中12的平衡因子为0,旋转后10和12和15平衡因子均为0。

3种情况:
- 插入到e那边
- 插入到f那边
- b本身就是插入的点
// 右左双旋
void RotateRL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;// 提前存放平衡因子int bf = subRL->_bf;RotateR(parent->_right);RotateL(parent);if (bf == -1){subRL->_bf = 0;parent->_bf = 0;subR->_bf = 1;}else if (bf == 1){subRL->_bf = 0;parent->_bf = -1;subR->_bf = 0;}else if (bf == 0){subRL->_bf = 0;parent->_bf = 0;subR->_bf = 0;}else{assert(false);}
}
判断是不是AVL树
用高度差的绝对值是否 <= 1来检查
// 算树的高度,左右子树高的那个加1
int _Height(Node* root)
{if (root == nullptr){return 0;}int leftHeight = _Height(root->_left);int rightHeight = _Height(root->_right);return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}// 判断是不是AVL树
bool _IsBalanceTree(Node* root)
{// 空树也是AVL树if (root == nullptr)return true;// pRoot的子树的平衡因子,左右子树的高度差int _leftheight = _Height(root->_left);int _rightheight = _Height(root->_right);int diff = _rightheight - _leftheight;// 高度差超过2或者pRoot的平衡因子不等于计算出的平衡因子就不是AVL树if (abs(diff) >= 2){cout << root->_kv.first << "高度差异常" << endl;return false;}else if (diff != root->_bf){cout << root->_kv.first << "平衡因子异常" << endl;return false;}// pRoot节点的左树和右树都是AVL树,那么就是AVL树return _IsBalanceTree(root->_left) && _IsBalanceTree(root->_right);
}
时间复杂度分析
插入:logN,寻找插入的位置,会找到叶子的位置
旋转:常数次
调整:假设最坏情况调整到根logN,平衡因子为-1/1,要继续调整
时间复杂度:logN
全部的代码
#pragma once
#include<iostream>
#include<assert.h>using namespace std;template<class K, class V>
struct AVLTreeNode
{// 需要parent指针pair<K, V> _kv;AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;AVLTreeNode<K, V>* _parent;int _bf;// 平衡因子AVLTreeNode(const pair<K, V>& kv):_kv(kv),_left(nullptr),_right(nullptr),_parent(nullptr),_bf(0)// 刚插入的节点平衡因子都是0{}
};template<class K, class V>
class AVLTree
{typedef AVLTreeNode<K, V> Node;
public:bool insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{// 不冗余return false;}}// 链接父节点cur = new Node(kv);if (parent->_kv.first < kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;// 更新平衡因子// 控制平衡while (parent){if (parent->_left == cur)parent->_bf--;else // if (parent->_right == cur)parent->_bf++;if (parent->_bf == 0){break;}else if (parent->_bf == -1 || parent->_bf == 1){cur = parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){// 旋转if (parent->_bf == -2 && cur->_bf == -1){// 右旋,左高右低RotateR(parent);}else if(parent->_bf == 2&&cur->_bf == 1){// 左旋,右高左低RotateL(parent);}else if(parent->_bf == -2&&cur->_bf == 1){// 左右双旋,右高左高RotateLR(parent);}else if (parent->_bf == 2 && cur->_bf == -1){// 右左双旋,左高右高RotateRL(parent);}else{assert(false);}break;}else{// 逻辑错误,之前就不是AVL树assert(false);}}return true;}// 右单旋,旋转点是parentvoid RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;// b可能为空树if (subLR != nullptr)subLR->_parent = parent;// 记录parent的parentNode* pParent = parent->_parent;subL->_right = parent;parent->_parent = subL;// 1. 10是这棵树的总根if (parent == _root){_root = subL;subL->_parent = nullptr;}else{// 2. 10是这棵树的局部根// pParent左可能是parent,右也可能是parentif (pParent->_left == parent){pParent->_left = subL;}else{pParent->_right = subL;}subL->_parent = pParent;}// 更新平衡因子subL->_bf = 0;parent->_bf = 0;}// 左单旋,旋转点是parentvoid RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;// b不是空树if (subRL)subRL->_parent = parent;// 记录父亲节点的父亲节点Node* pParent = parent->_parent;subR->_left = parent;parent->_parent = subR;// 1. 10是这棵树的总根if (_root == parent){_root = subR;subR->_parent = nullptr;}else{// 2. 10是这棵树的局部根if (pParent->_left == parent){pParent->_left = subR;}else{pParent->_right = subR;}subR->_parent = pParent;}subR->_bf = 0;parent->_bf = 0;}// 左右双旋void RotateLR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;// 提前存平衡因子int bf = subLR->_bf;RotateL(parent->_left);RotateR(parent);if (subLR->_bf == -1){subLR->_bf = 0;subL->_bf = 0;parent->_bf = 1;}else if (subLR->_bf == 1){subLR->_bf = 0;subL->_bf = -1;parent->_bf = 0;}else if (subLR->_bf == 0){subLR->_bf = 0;subL->_bf = 0;parent->_bf = 0;}else{assert(false);}}// 右左双旋void RotateRL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;// 提前存放平衡因子int bf = subRL->_bf;RotateR(parent->_right);RotateL(parent);if (bf == -1){subRL->_bf = 0;parent->_bf = 0;subR->_bf = 1;}else if (bf == 1){subRL->_bf = 0;parent->_bf = -1;subR->_bf = 0;}else if (bf == 0){subRL->_bf = 0;parent->_bf = 0;subR->_bf = 0;}else{assert(false);}}Node* Find(const K& key){Node* cur = _root;while (cur){if (cur->_kv.first < key){cur = cur->_right;}else if (cur->_kv.first > key){cur = cur->_left;}else{return cur;}}return nullptr;}// 大小int Size(){return _Size(_root);}// 判断是不是AVL树bool IsBalanceTree(){return _IsBalanceTree(_root);}// 算树的高度int Height(){_Height(_root);}// 中序void InOrder(){_InOrder(_root);cout << endl;}
private:// 算树的高度,左右子树高的那个加1int _Height(Node* root){if (root == nullptr){return 0;}int leftHeight = _Height(root->_left);int rightHeight = _Height(root->_right);return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;}// 算树的节点个数 int _Size(Node* root){if (root == nullptr)return 0;return _Size(root->_left) + _Size(root->_right) + 1;}// 判断是不是AVL树bool _IsBalanceTree(Node* root){// 空树也是AVL树if (root == nullptr)return true;// pRoot的子树的平衡因子,左右子树的高度差int _leftheight = _Height(root->_left);int _rightheight = _Height(root->_right);int diff = _rightheight - _leftheight;// 高度差超过2或者pRoot的平衡因子不等于计算出的平衡因子就不是AVL树if (abs(diff) >= 2){cout << root->_kv.first << "高度差异常" << endl;return false;}else if (diff != root->_bf){cout << root->_kv.first << "平衡因子异常" << endl;return false;}// pRoot节点的左树和右树都是AVL树,那么就是AVL树return _IsBalanceTree(root->_left) && _IsBalanceTree(root->_right);}void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);cout << root->_kv.first << ":" << root->_kv.second << endl;_InOrder(root->_right);}private:Node* _root = nullptr;
};#include"AVLTree.h"void TestAVLTree1()
{AVLTree<int, int> t;// 常规的测试⽤例int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };// 特殊的带有双旋场景的测试⽤例//int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };for (auto e : a){t.insert({ e, e });}t.InOrder();cout << t.IsBalanceTree() << endl;
}int main()
{TestAVLTree1();return 0;
}
相关文章:

C++AVL树(二)详解
文章目录 AVL树旋转单旋右单旋左单旋 双旋左右双旋右左双旋 平衡因子的更新左右双旋右左双旋 判断是不是AVL树时间复杂度分析全部的代码 AVL树 旋转 单旋 单旋是纯粹的一边高 单旋平衡因子是同号 右单旋 a,b,c自身不能发生旋转 并且也不能不向上继续更新(不能停…...

RocketMQ 的 Topic 和消息队列MessageQueue信息,是怎么分布到Broker的?怎么负载均衡到Broker的?
目录 1. Topic 和 MessageQueue 的基本概念 1.1 Topic 1.2 MessageQueue 2. Topic 和 MessageQueue 的分布 2.1 Topic 的创建 2.2 MessageQueue 分配到 Broker 2.3 分布规则 3. 负载均衡机制 3.1 Producer 的负载均衡 3.2 Consumer 的负载均衡 3.3 Broker 的负载均衡…...

无人机核心项目开发系列:从设计到实现的完整解析
无人机核心项目开发系列:从设计到实现的完整解析 01-面试大保健-核心项目-无人机-架构-硬件 1. 无人机项目概述 在这篇博客中,我们将回顾一个遥控四轴无人机的项目。这是一个面向儿童的玩具无人机,具备基础的飞行功能:上升、下…...

浅谈Redis
2007 年,一位程序员和朋友一起创建了一个网站。为了解决这个网站的负载问题,他自己定制了一个数据库。于2009 年开发,称之为Redis。这位意大利程序员是萨尔瓦托勒桑菲利波(Salvatore Sanfilippo),他被称为Redis之父,更…...

Ceisum无人机巡检直播视频投射
接上次的视频投影,Leader告诉我这个视频投影要用在两个地方,一个是我原先写的轨迹回放那里,另一个在无人机起飞后的地图回显,要实时播放无人机拍摄的视频,还要能转镜头,让我把这个也接一下。 我的天&#x…...

【组件库】使用Vue2+AntV X6+ElementUI 实现拖拽配置自定义vue节点
先来看看实现效果: 【组件库】使用 AntV X6 ElementUI 实现拖拽配置自定义 Vue 节点 在现代前端开发中,流程图和可视化编辑器的需求日益增加。AntV X6 是一个强大的图形化框架,支持丰富的图形操作和自定义功能。结合 ElementUI,…...

Vue.js组件开发-如何实现全选反选
在 Vue.js 中实现全选和反选功能,可以通过结合v-model、计算属性和事件处理来完成。 实现思路 • 数据绑定:为每个复选框绑定一个选中状态。 • 全选控制:通过一个复选框控制所有复选框的选中状态。 • 反选控制:通过一个按钮或…...

2025.1.20——四、[强网杯 2019]Upload1 文件上传|反序列化
题目来源:buuctf [强网杯 2019]Upload 1 目录 一、打开靶机,查看信息 二、解题思路 step 1:登陆进去看情况 step 2:大佬来支援——问题在cookie step 3:测试两个思路 1.目录穿越 2.目录扫描 step 4ÿ…...

php代码审计2 piwigo CMS in_array()函数漏洞
php代码审计2 piwigo CMS in_array()函数漏洞 一、目的 本次学习目的是了解in_array()函数和对项目piwigo中关于in_array()函数存在漏洞的一个审计并利用漏洞获得管理员帐号。 二、in_array函数学习 in_array() 函数搜索数组中是否存在指定的值。 in_array($search,$array…...
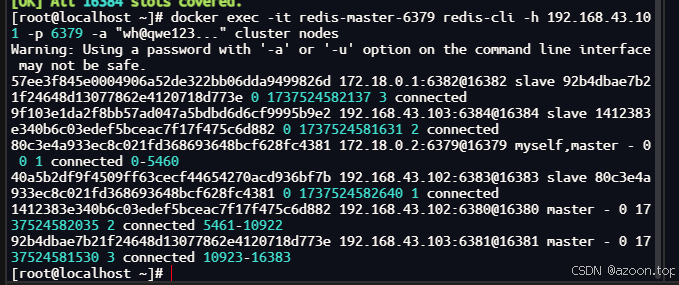
docker搭建redis集群(三主三从)
本篇文章不包含理论解释,直接开始集群(三主三从)搭建 环境 centos7 docker 26.1.4 redis latest (7.4.2) 服务器搭建以及环境配置 请查看本系列前几篇博客 默认已搭建好三个虚拟机并安装配置好docker 相关博客…...
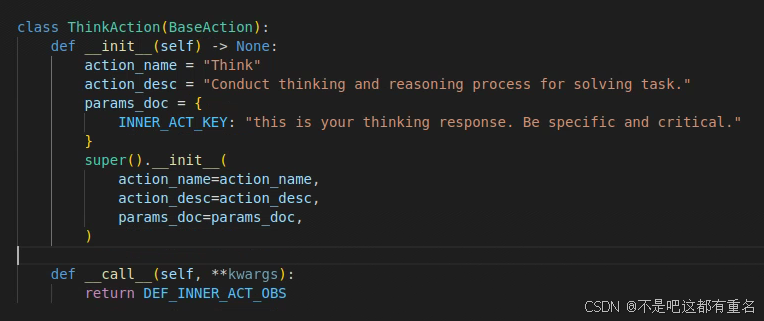
[Datawheel]利用Zigent框架编写智能体-1
1.背景知识 1.1 什么是zigent? Zigent 是一个多智能体框架,旨在简化和优化智能体的开发与部署。Zigent 是由 自塾(Zishu.co) 团队开发的一个开源项目。自塾在 2024 年推出了多个开源项目,其中包括 wow-agent…...

【计算机视觉】人脸识别
一、简介 人脸识别是将图像或者视频帧中的人脸与数据库中的人脸进行对比,判断输入人脸是否与数据库中的某一张人脸匹配,即判断输入人脸是谁或者判断输入人脸是否是数据库中的某个人。 人脸识别属于1:N的比对,输入人脸身份是1&…...

linux环境变量配置文件区别 /etc/profile和~/.bash_profile
在 Linux 系统中,环境变量可以定义用户会话的行为,而这些变量的加载和配置通常涉及多个文件,如 ~/.bash_profile 和 /etc/profile。这些文件的作用和加载时机各有不同。以下是对它们的详细区别和用途的说明: 文章目录 1. 环境变量…...

mac 配置 python 环境变量
最新 mac 电脑,配置原理暂未研究,欢迎答疑 方案一 获取python的安装路径 which python3 配置环境变量 open ~/.bash_profile 末尾添加: PATH"/Library/Frameworks/Python.framework/Versions/3.13/bin:${PATH}" export PATH …...
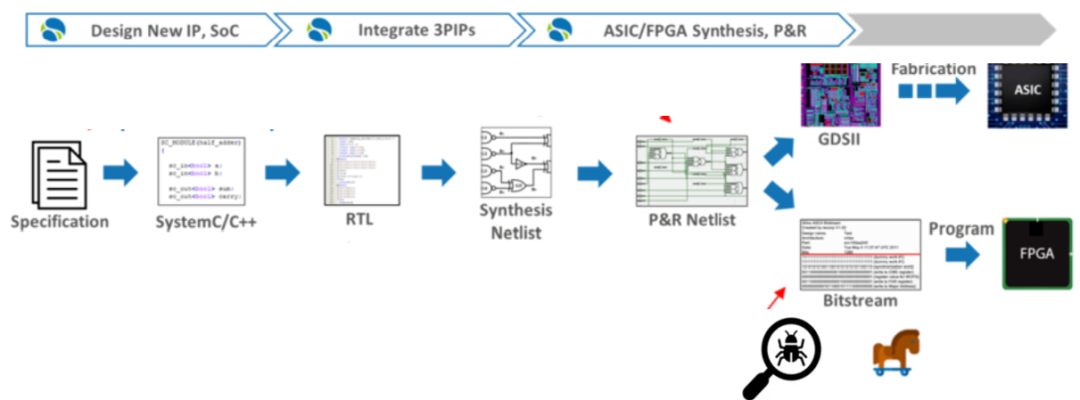
终极的复杂,是简单
软件仿真拥有最佳的信号可见性和调试灵活性,能够高效捕获很多显而易见的常见错误,被大多数工程师熟练使用。 空间领域应用的一套数据处理系统(Data Handling System),采用抗辐FPGA作为主处理器,片上资源只包含10752个寄存器,软仿也是个挺花时间的事。 Few ms might take …...
)
软件开发中的密码学(国密算法)
1.软件行业中的加解密 在软件行业中,加解密技术广泛应用于数据保护、通信安全、身份验证等多个领域。加密(Encryption)是将明文数据转换为密文的过程,而解密(Decryption)则是将密文恢复为明文的过程。以下…...

【豆包MarsCode 蛇年编程大作战】蛇形烟花
项目体验地址:项目体验地址 官方活动地址:活动地址 目录 【豆包MarsCode 蛇年编程大作战】蛇形烟花演示 引言 豆包 MarsCode介绍 项目准备 第一步:安装插件 第二步:点击豆包图标来进行使用豆包 使用豆包 MarsCodeAI助手实…...
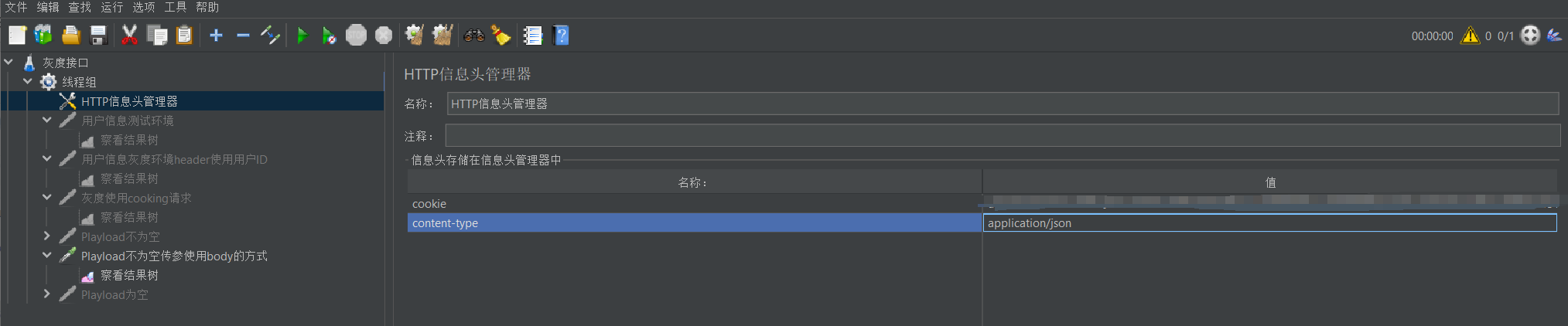
Jmeter使用Request URL请求接口
简介 在Jmeter调试接口时,有时不清楚后端服务接口的具体路径,可以使用Request URL和cookie来实现接口请求。以下内容以使用cookie鉴权的接口举例。 步骤 ① 登录网站后获取具体的Request URL和cookie信息 通过浏览器获取到Request URL和cookie&#…...

使用Pytest Fixtures来提升TestCase的可读性、高效性
关注开源优测不迷路 大数据测试过程、策略及挑战 测试框架原理,构建成功的基石 在自动化测试工作之前,你应该知道的10条建议 在自动化测试中,重要的不是工具 在编写单元测试时,你是否发现自己有很多重复代码? 数据库设…...
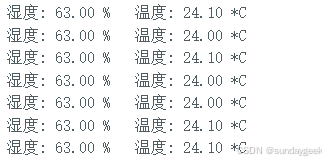
Arduino大师练成手册 -- 读取DHT11
要在 Arduino 上控制 DHT11 温湿度传感器,你可以按照以下步骤进行: 硬件连接: 将 DHT11 的 VCC 引脚连接到 Arduino 的 5V 引脚。 将 DHT11 的 GND 引脚连接到 Arduino 的 GND 引脚。 将 DHT11 的 DATA 引脚连接到 Arduino 的数字引脚&am…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...
