论文阅读的附录(七):Understanding Diffusion Models: A Unified Perspective(二):公式46的推导
Understanding Diffusion Models: A Unified Perspective(二):公式46的推导
- 文章概括
- 要推导的公式
- 1. 条件概率的定义
- 2. 联合分布的分解
- 2.1 联合分布的定义
- 2.2 为什么可以这样分解?
- 2.3 具体意义
- 3. 分母的分解:边际化规则
- 4. 最终公式的推导
- 5. 为什么分母可以表示为 q ( x t − 1 ∣ x 0 ) q(x_{t-1}|x_0) q(xt−1∣x0)
- 6. 公式 (46) 的最终形式
- 7. 逐步推导总结
文章概括
引用:
@article{luo2022understanding,title={Understanding diffusion models: A unified perspective},author={Luo, Calvin},journal={arXiv preprint arXiv:2208.11970},year={2022}
}
Luo, C., 2022. Understanding diffusion models: A unified perspective. arXiv preprint arXiv:2208.11970.
原文: https://arxiv.org/abs/2208.11970
代码、数据和视频:https://arxiv.org/abs/2208.11970
文章解析原文:
论文笔记(六十三)Understanding Diffusion Models: A Unified Perspective(二)
要推导的公式
目标是推导公式:
q ( x t ∣ x t − 1 , x 0 ) = q ( x t − 1 ∣ x t , x 0 ) q ( x t ∣ x 0 ) q ( x t − 1 ∣ x 0 ) . (46) q(x_t|x_{t-1}, x_0) = \frac{q(x_{t-1}|x_t, x_0) q(x_t|x_0)}{q(x_{t-1}|x_0)}. \tag{46} q(xt∣xt−1,x0)=q(xt−1∣x0)q(xt−1∣xt,x0)q(xt∣x0).(46)
1. 条件概率的定义
条件概率的基本定义为:
q ( A ∣ B ) = q ( A ∩ B ) q ( B ) , 其中 q ( B ) > 0. q(A|B) = \frac{q(A \cap B)}{q(B)}, \quad \text{其中 } q(B) > 0. q(A∣B)=q(B)q(A∩B),其中 q(B)>0.
对于多个条件的情况,比如 ( q(A|B, C) ),可以扩展为:
q ( A ∣ B , C ) = q ( A , B , C ) q ( B , C ) . q(A|B, C) = \frac{q(A, B, C)}{q(B, C)}. q(A∣B,C)=q(B,C)q(A,B,C).
在我们的目标公式中, q ( x t ∣ x t − 1 , x 0 ) q(x_t|x_{t-1}, x_0) q(xt∣xt−1,x0) 表示在 x t − 1 x_{t-1} xt−1 和 x 0 x_0 x0 已知的条件下, x t x_t xt 的分布。因此:
q ( x t ∣ x t − 1 , x 0 ) = q ( x t , x t − 1 , x 0 ) q ( x t − 1 , x 0 ) . (1) q(x_t|x_{t-1}, x_0) = \frac{q(x_t, x_{t-1}, x_0)}{q(x_{t-1}, x_0)}. \tag{1} q(xt∣xt−1,x0)=q(xt−1,x0)q(xt,xt−1,x0).(1)
2. 联合分布的分解
我们需要分解联合分布 q ( x t , x t − 1 , x 0 ) q(x_t, x_{t-1}, x_0) q(xt,xt−1,x0)。以下是基础逻辑:
2.1 联合分布的定义
联合分布 q ( x t , x t − 1 , x 0 ) q(x_t, x_{t-1}, x_0) q(xt,xt−1,x0) 表示 x t , x t − 1 , x 0 x_t, x_{t-1}, x_0 xt,xt−1,x0 同时发生的概率。根据 概率链式法则(Chain Rule of Probability),联合分布可以逐步分解为条件概率的乘积:
q ( x t , x t − 1 , x 0 ) = q ( x t − 1 ∣ x t , x 0 ) q ( x t ∣ x 0 ) . (2) q(x_t, x_{t-1}, x_0) = q(x_{t-1}|x_t, x_0) q(x_t|x_0). \tag{2} q(xt,xt−1,x0)=q(xt−1∣xt,x0)q(xt∣x0).(2)
这一步基于条件概率的定义:
- q ( x t − 1 ∣ x t , x 0 ) q(x_{t-1}|x_t, x_0) q(xt−1∣xt,x0):在 x t x_t xt 和 x 0 x_0 x0 已知的条件下, x t − 1 x_{t-1} xt−1 的分布。
- q ( x t ∣ x 0 ) q(x_t|x_0) q(xt∣x0):在 x 0 x_0 x0 已知的情况下, x t x_t xt 的边际分布。
2.2 为什么可以这样分解?
根据概率论的链式规则:
q ( A , B , C ) = q ( A ∣ B , C ) q ( B , C ) . q(A, B, C) = q(A|B, C) q(B, C). q(A,B,C)=q(A∣B,C)q(B,C).
在这里,设 A = x t − 1 A = x_{t-1} A=xt−1, B = x t B = x_t B=xt, C = x 0 C = x_0 C=x0,我们可以写成:
q ( x t − 1 , x t , x 0 ) = q ( x t − 1 ∣ x t , x 0 ) q ( x t , x 0 ) . q(x_{t-1}, x_t, x_0) = q(x_{t-1}|x_t, x_0) q(x_t, x_0). q(xt−1,xt,x0)=q(xt−1∣xt,x0)q(xt,x0).
接着,再对 q ( x t , x 0 ) q(x_t, x_0) q(xt,x0) 应用链式规则:
q ( x t , x 0 ) = q ( x t ∣ x 0 ) q ( x 0 ) . q(x_t, x_0) = q(x_t|x_0) q(x_0). q(xt,x0)=q(xt∣x0)q(x0).
因此:
q ( x t − 1 , x t , x 0 ) = q ( x t − 1 ∣ x t , x 0 ) q ( x t ∣ x 0 ) q ( x 0 ) . q(x_{t-1}, x_t, x_0) = q(x_{t-1}|x_t, x_0) q(x_t|x_0) q(x_0). q(xt−1,xt,x0)=q(xt−1∣xt,x0)q(xt∣x0)q(x0).
在本问题中, q ( x 0 ) q(x_0) q(x0) 是常量,不影响条件概率的形式,所以我们可以简化为:
q ( x t , x t − 1 , x 0 ) = q ( x t − 1 ∣ x t , x 0 ) q ( x t ∣ x 0 ) . q(x_t, x_{t-1}, x_0) = q(x_{t-1}|x_t, x_0) q(x_t|x_0). q(xt,xt−1,x0)=q(xt−1∣xt,x0)q(xt∣x0).
2.3 具体意义
-
分解的直观意义:假设我们已经知道 x t x_t xt 和全局变量 x 0 x_0 x0 的值,那么我们可以首先用 q ( x t − 1 ∣ x t , x 0 ) q(x_{t-1}|x_t, x_0) q(xt−1∣xt,x0) 表示 x t − 1 x_{t-1} xt−1 的条件概率,再用 q ( x t ∣ x 0 ) q(x_t|x_0) q(xt∣x0) 表示 x t x_t xt 的边际分布。
-
为什么分解成这两项?
- 这是因为 q ( x t ∣ x 0 ) q(x_t|x_0) q(xt∣x0) 表示的是全局信息(全局分布)。
- 而 q ( x t − 1 ∣ x t , x 0 ) q(x_{t-1}|x_t, x_0) q(xt−1∣xt,x0) 捕捉的是局部的条件关系。
3. 分母的分解:边际化规则
分母 q ( x t − 1 , x 0 ) q(x_{t-1}, x_0) q(xt−1,x0) 是 x t − 1 x_{t-1} xt−1 和 x 0 x_0 x0 的联合分布,可以通过边际化 x t x_t xt 得到:
q ( x t − 1 , x 0 ) = ∫ q ( x t , x t − 1 , x 0 ) d x t . (4) q(x_{t-1}, x_0) = \int q(x_t, x_{t-1}, x_0) dx_t. \tag{4} q(xt−1,x0)=∫q(xt,xt−1,x0)dxt.(4)
将公式 (2) 中的分解 q ( x t , x t − 1 , x 0 ) = q ( x t − 1 ∣ x t , x 0 ) q ( x t ∣ x 0 ) q(x_t, x_{t-1}, x_0) = q(x_{t-1}|x_t, x_0) q(x_t|x_0) q(xt,xt−1,x0)=q(xt−1∣xt,x0)q(xt∣x0) 代入公式 (4):
q ( x t − 1 , x 0 ) = ∫ q ( x t − 1 ∣ x t , x 0 ) q ( x t ∣ x 0 ) d x t . (5) q(x_{t-1}, x_0) = \int q(x_{t-1}|x_t, x_0) q(x_t|x_0) dx_t. \tag{5} q(xt−1,x0)=∫q(xt−1∣xt,x0)q(xt∣x0)dxt.(5)
4. 最终公式的推导
将公式 (5) 的分母代入公式 (3),得到:
q ( x t ∣ x t − 1 , x 0 ) = q ( x t − 1 ∣ x t , x 0 ) q ( x t ∣ x 0 ) ∫ q ( x t − 1 ∣ x t , x 0 ) q ( x t ∣ x 0 ) d x t . q(x_t|x_{t-1}, x_0) = \frac{q(x_{t-1}|x_t, x_0) q(x_t|x_0)}{\int q(x_{t-1}|x_t, x_0) q(x_t|x_0) dx_t}. q(xt∣xt−1,x0)=∫q(xt−1∣xt,x0)q(xt∣x0)dxtq(xt−1∣xt,x0)q(xt∣x0).
现在,我们需要注意的是:
- 分子部分完全匹配公式 (46)。
- 分母部分的归一化形式也与公式 (46) 一致。
为了便于理解,分母中的积分项 ∫ q ( x t − 1 ∣ x t , x 0 ) q ( x t ∣ x 0 ) d x t \int q(x_{t-1}|x_t, x_0) q(x_t|x_0) dx_t ∫q(xt−1∣xt,x0)q(xt∣x0)dxt 在公式 (46) 中直接用 q ( x t − 1 ∣ x 0 ) q(x_{t-1}|x_0) q(xt−1∣x0) 表示。
5. 为什么分母可以表示为 q ( x t − 1 ∣ x 0 ) q(x_{t-1}|x_0) q(xt−1∣x0)
通过边际化定义:
q ( x t − 1 ∣ x 0 ) = ∫ q ( x t − 1 , x t ∣ x 0 ) d x t . q(x_{t-1}|x_0) = \int q(x_{t-1}, x_t|x_0) dx_t. q(xt−1∣x0)=∫q(xt−1,xt∣x0)dxt.
进一步分解 q ( x t − 1 , x t ∣ x 0 ) q(x_{t-1}, x_t|x_0) q(xt−1,xt∣x0):
q ( x t − 1 , x t ∣ x 0 ) = q ( x t − 1 ∣ x t , x 0 ) q ( x t ∣ x 0 ) . q(x_{t-1}, x_t|x_0) = q(x_{t-1}|x_t, x_0) q(x_t|x_0). q(xt−1,xt∣x0)=q(xt−1∣xt,x0)q(xt∣x0).
1. 条件概率的链式规则
根据条件概率的定义,联合概率 q ( A , B ∣ C ) q(A, B|C) q(A,B∣C) 可以分解为: q ( A , B ∣ C ) = q ( A ∣ B , C ) q ( B ∣ C ) . q(A, B|C) = q(A|B, C) q(B|C). q(A,B∣C)=q(A∣B,C)q(B∣C).
符号解释:
- q ( A , B ∣ C ) q(A, B|C) q(A,B∣C):表示在 C C C 已知的条件下,事件 A A A 和 B B B 同时发生的概率。
- q ( A ∣ B , C ) q(A|B, C) q(A∣B,C):表示在 B B B 和 C C C 已知的条件下,事件 A A A 的条件概率。
- q ( B ∣ C ) q(B|C) q(B∣C):表示在 C C C 已知的条件下,事件 B B B 的条件概率。
代入后得到:
q ( x t − 1 ∣ x 0 ) = ∫ q ( x t − 1 ∣ x t , x 0 ) q ( x t ∣ x 0 ) d x t . q(x_{t-1}|x_0) = \int q(x_{t-1}|x_t, x_0) q(x_t|x_0) dx_t. q(xt−1∣x0)=∫q(xt−1∣xt,x0)q(xt∣x0)dxt.
因此,分母 q ( x t − 1 ∣ x 0 ) q(x_{t-1}|x_0) q(xt−1∣x0) 确实是公式 (46) 中的形式。
6. 公式 (46) 的最终形式
结合以上推导,公式 (46) 的最终形式是:
q ( x t ∣ x t − 1 , x 0 ) = q ( x t − 1 ∣ x t , x 0 ) q ( x t ∣ x 0 ) q ( x t − 1 ∣ x 0 ) . q(x_t|x_{t-1}, x_0) = \frac{q(x_{t-1}|x_t, x_0) q(x_t|x_0)}{q(x_{t-1}|x_0)}. q(xt∣xt−1,x0)=q(xt−1∣x0)q(xt−1∣xt,x0)q(xt∣x0).
7. 逐步推导总结
-
从条件概率的定义出发:
q ( x t ∣ x t − 1 , x 0 ) = q ( x t , x t − 1 , x 0 ) q ( x t − 1 , x 0 ) . q(x_t|x_{t-1}, x_0) = \frac{q(x_t, x_{t-1}, x_0)}{q(x_{t-1}, x_0)}. q(xt∣xt−1,x0)=q(xt−1,x0)q(xt,xt−1,x0). -
联合分布的分解:
q ( x t , x t − 1 , x 0 ) = q ( x t − 1 ∣ x t , x 0 ) q ( x t ∣ x 0 ) . q(x_t, x_{t-1}, x_0) = q(x_{t-1}|x_t, x_0) q(x_t|x_0). q(xt,xt−1,x0)=q(xt−1∣xt,x0)q(xt∣x0). -
分母的边际化:
q ( x t − 1 , x 0 ) = ∫ q ( x t − 1 ∣ x t , x 0 ) q ( x t ∣ x 0 ) d x t . q(x_{t-1}, x_0) = \int q(x_{t-1}|x_t, x_0) q(x_t|x_0) dx_t. q(xt−1,x0)=∫q(xt−1∣xt,x0)q(xt∣x0)dxt. -
最终公式的组合:
q ( x t ∣ x t − 1 , x 0 ) = q ( x t − 1 ∣ x t , x 0 ) q ( x t ∣ x 0 ) q ( x t − 1 ∣ x 0 ) . q(x_t|x_{t-1}, x_0) = \frac{q(x_{t-1}|x_t, x_0) q(x_t|x_0)}{q(x_{t-1}|x_0)}. q(xt∣xt−1,x0)=q(xt−1∣x0)q(xt−1∣xt,x0)q(xt∣x0).
相关文章:
:Understanding Diffusion Models: A Unified Perspective(二):公式46的推导)
论文阅读的附录(七):Understanding Diffusion Models: A Unified Perspective(二):公式46的推导
Understanding Diffusion Models: A Unified Perspective(二):公式46的推导 文章概括要推导的公式1. 条件概率的定义2. 联合分布的分解2.1 联合分布的定义2.2 为什么可以这样分解?2.3 具体意义 3. 分母的分解:边际化规…...

BGP分解实验·12——配置路由反射器
当一个AS包含多个iBGP对等体时,路由反射器(Route-Reflector)非常有用,因为相对于iBGP路由反射器指定的客户端只需要和路由反射器建立邻居关系,从而降低了iBGP全互连的连接数量。路由反射器(RR)和…...

PCIe 个人理解专栏——【2】LTSSM(Link Training and Status State Machine)
前言: 链路训练和状况状态机LTSSM(Link Training and Status State Machine)是整个链路训练和运行中状态的状态转换逻辑关系图,总共有11个状态。 正文: 包括检测(Detect),轮询&…...

cmake 编译QT之JKQtPlotter-4.0.3
cmake 编译 JKQtPlotter-4.0.3 1.下载源码 源码地址:https://github.com/jkriege2/JKQtPlotter 2.编译 mkdir build cd buildDCMAKE_PREFIX_PATH指编译器目录 D:\ProgramFiles\cmake-3.25.0-rc1-windows-i386\bin\cmake.exe -G "Visual Studio 16 2019&qu…...

【C】memory 详解
<memory.h> 是一个 C 标准库头文件,提供了一组内存管理函数,用于分配、释放和操作动态内存。这些函数主要操作的是未初始化的内存块,是早期 C 编程中常用的内存操作工具。 尽管在现代 C 编程中更推荐使用<cstring>或<memory&…...
Python 爬虫 - Selenium 框架
Python 爬虫 - Selenium 框架 安装安装 Selenium安装 WebDriver 操作浏览器打开浏览器普通方式加载配置方式Headless 方式 设置浏览器窗口最大化显示最小化显示自定义大小 前进后退前进后退 元素定位根据 id 定位根据 name 定位根据 class 定位根据标签名定位使用 CSS 定位使用…...

mysql的having语句
MySQL的HAVING语句用于在GROUP BY子句对数据进行分组后,过滤满足特定条件的组。与WHERE子句不同,HAVING子句可以在过滤条件中使用聚合函数,而WHERE子句则不能。通常,HAVING子句与GROUP BY子句一起使用,以实现对分组数据…...

华为数据之道-读书笔记
内容简介 关键字 数字化生产 已经成为普遍的商业模式,其本质是以数据为处理对象,以ICT平台为生产工具,以软件为载体,以服务为目的的生产过程。 信息与通信技术平台(Information and Communication Technology Platf…...
CDN、源站与边缘网络
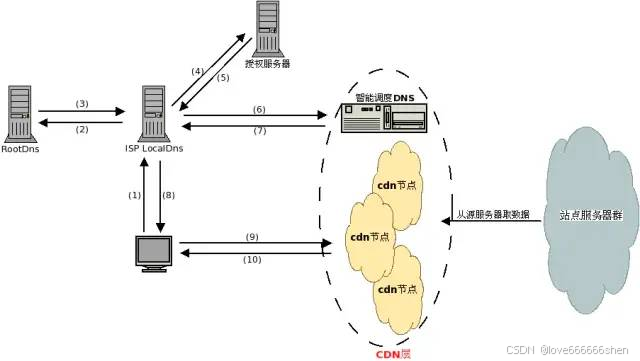
什么是“源站” 源服务器 源服务器的目的是处理和响应来自互联网客户端的传入请求。源服务器的概念通常与边缘服务器或缓存服务器的概念结合使用。源服务器的核心是一台运行一个或多个程序的计算机,这些程序旨在侦听和处理传入的客户端请求。源服务器可以承担为网…...
工业相机 SDK 二次开发-Sherlock插件
本文介绍了 sherlock 连接相机时的插件使用。通过本套插件可连接海康的工业相机。 一.环境配置 1. 拷贝动态库 在用户安装 MVS 目录下按照如下路径 Development\ThirdPartyPlatformAdapter 找到目 录为 DalsaSherlock 的文件夹,根据 Sherlock 版本找到…...
FlinkSql使用中rank/dense_rank函数报错空指针
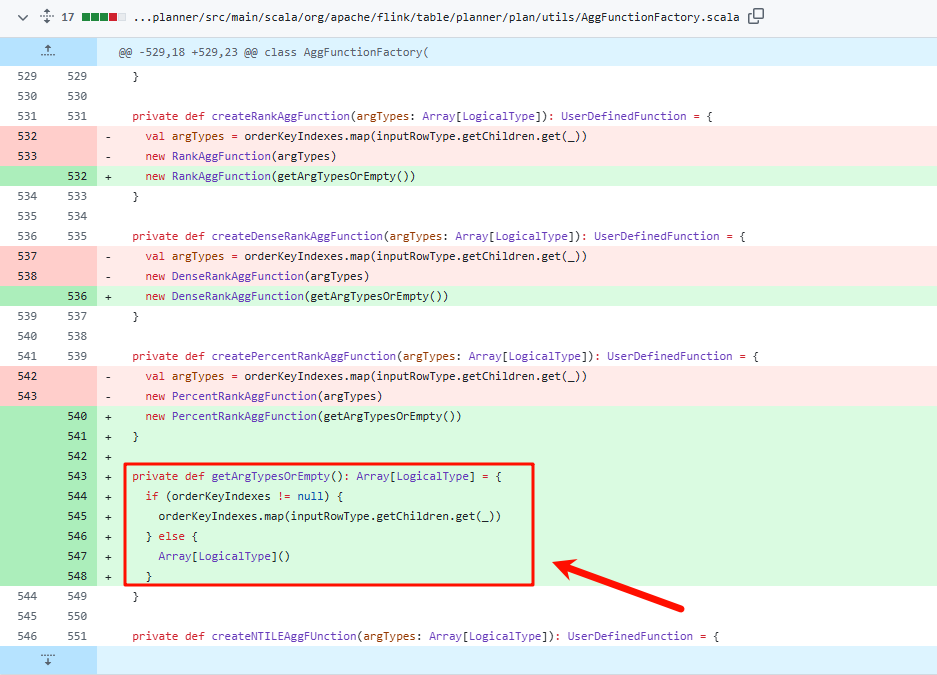
问题描述 在flink1.16(甚至以前的版本)中,使用rank()或者dense_rank()进行排序时,某些场景会导致报错空指针NPE(NullPointerError) 报错内容如下 该报错没有行号/错误位置,无法排查 现状 目前已经确认为bug,根据github上的PR日…...
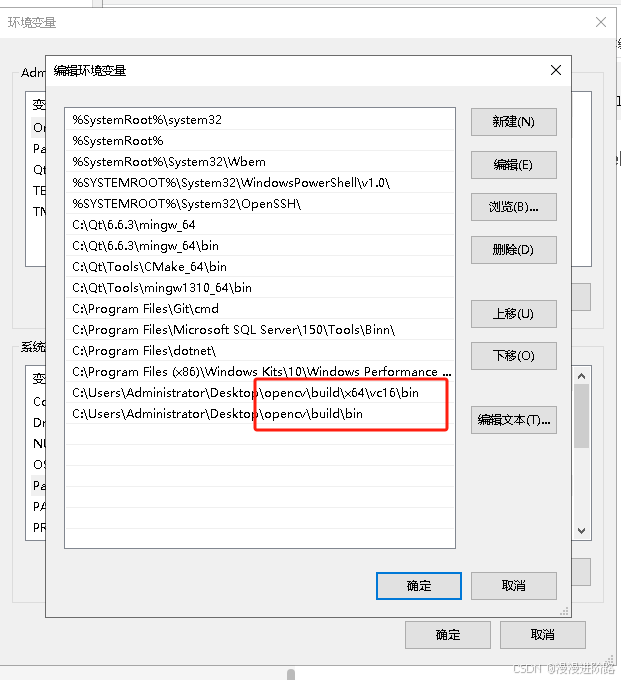
VS C++ 配置OPENCV环境
VS C 配置OPENCV环境 1.下载opencv2.安装环境3.opencv环境4.VS配置opencv环境5.EXE执行文件路径的环境lib和dll需要根据是debug还是release环境来区分使用哪个 6.Windows环境 1.下载opencv 链接: link 2.安装环境 双击运行即可 3.opencv环境 include文件路径:opencv\build\…...
【SpringSecurity】基本开发流程
文章目录 概要整体架构流程实现流程1、编写各种Handler2 、AccessToken处理器3、定义AuthenticationFilter 继承 OncePerRequestFilter (OncePerRequestFilter是Spring提供的一个过滤器基类,它确保了在一次完整的HTTP请求中,无论请求经过多少…...
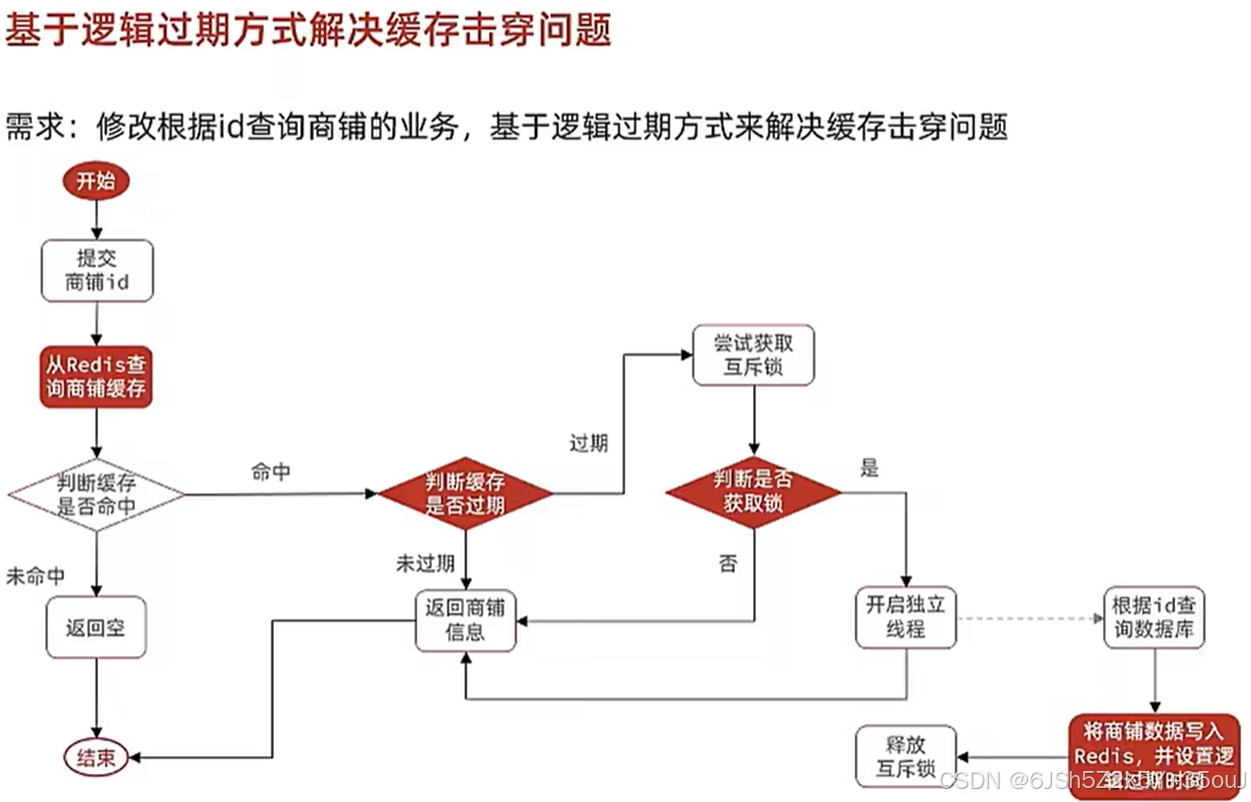
Redis实战(黑马点评)——关于缓存(缓存更新策略、缓存穿透、缓存雪崩、缓存击穿、Redis工具)
redis实现查询缓存的业务逻辑 service层实现 Overridepublic Result queryById(Long id) {String key CACHE_SHOP_KEY id;// 现查询redis内有没有数据String shopJson (String) redisTemplate.opsForValue().get(key);if(StrUtil.isNotBlank(shopJson)){ // 如果redis的数…...

ChatGPT从数据分析到内容写作建议相关的46个提示词分享!
在当今快节奏的学术环境中,研究人员面临着海量的信息和复杂的研究任务。幸运的是,随着人工智能技术的发展,像ChatGPT这样的先进工具为科研人员提供了强大的支持。今天就让我们一起探索如何利用ChatGPT提升研究效率进一步优化研究流程。 ChatG…...

在 Windows 11 中设置 WSL2 Ubuntu 的 `networkingMode=mirrored` 详细教程
在 Windows 11 中设置 WSL2 Ubuntu 的 networkingModemirrored 详细教程 引言环境要求配置 .wslconfig 文件重启 WSL2验证镜像网络模式解决常见问题其他注意事项结论 引言 在 Windows 11 中使用 WSL2(Windows Subsystem for Linux 2)时,默认…...
万字长文总结前端开发知识---JavaScriptVue3Axios
JavaScript学习目录 一、JavaScript1. 引入方式1.1 内部脚本 (Inline Script)1.2 外部脚本 (External Script) 2. 基础语法2.1 声明变量2.2 声明常量2.3 输出信息 3. 数据类型3.1 基本数据类型3.2 模板字符串 4. 函数4.1 具名函数 (Named Function)4.2 匿名函数 (Anonymous Fun…...

怎么样把pdf转成图片模式(不能复制文字)
贵但好用的wps, 转换——转为图片型pdf —————————————————————————————————————————— 转换前: 转换后: 肉眼可见,模糊了,且不能复制。 其他免费办法,参考&…...
本地centos网络配置
1、路径 2、配置 另外还需要...

kotlin内联函数——runCatching
1.runCatching作用 代替try{}catch{}异常处理,用于捕获异常。 2.runCatching函数介绍 参数:上下文引用对象为参数返回值:lamda表达式结果 调用runCatching函数,如果调用成功则返回其封装的结果,并可回调onSuccess函…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...
