动态规划——斜率优化DP
题目清单
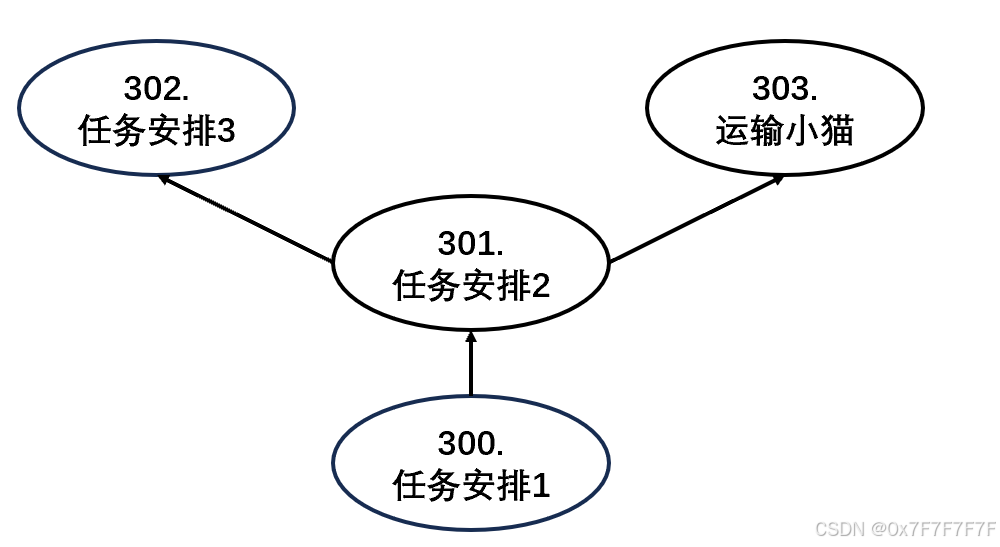
acwing300.任务安排1
状态表示f[i]:
集合:完成前i个任务且第i个任务为最后一个批次最后一个任务的方案。
属性:min
状态计算:
f [ i ] = m i n { f [ j ] + s u m t [ i ] × ∑ j + 1 i w [ u ] + s × ∑ j + 1 n w [ i ] } f[i]=min\{f[j]+sumt[i] ×\sum_{j+1}^{i}w[u]+s×\sum_{j+1}^{n}w[i]\} f[i]=min{f[j]+sumt[i]×∑j+1iw[u]+s×∑j+1nw[i]} ( 0 ≤ j < i ) (0\leq j < i) (0≤j<i)
f [ i ] = m i n { f [ j ] + s u m t [ i ] × ( s u m c [ i ] − s u m c [ j ] ) + s × ( s u m c [ n ] − s u m c [ j ] ) } f[i]=min\{f[j]+sumt[i] ×(sumc[i]-sumc[j])+s×(sumc[n]-sumc[j])\} f[i]=min{f[j]+sumt[i]×(sumc[i]−sumc[j])+s×(sumc[n]−sumc[j])} ( 0 ≤ j < i ) (0\leq j < i) (0≤j<i)
时间复杂度为 O ( n 2 ) O(n^2) O(n2)
#include <iostream>
#include <cstring>
using namespace std;
const int N = 5010;
typedef long long ll;
ll f[N];
ll sumt[N], sumc[N];
int n, s;
int main()
{cin >> n >> s;for (int i = 1; i <= n; i ++ ){scanf("%lld%lld", &sumt[i], &sumc[i]);sumt[i] += sumt[i - 1];sumc[i] += sumc[i - 1];}memset(f, 0x3f, sizeof f);f[0] = 0;for (int i = 1; i <= n; i ++ ){for (int j = 0; j < i; j ++ ){f[i] = min(f[i], f[j] + sumt[i] * (sumc[i] - sumc[j]) + s * (sumc[n] - sumc[j]));}}cout << f[n];return 0;
}
acwing301.任务安排2
我们对上一题得到的状态转移方程 f [ i ] = m i n { f [ j ] + s u m t [ i ] × ( s u m c [ i ] − s u m c [ j ] ) + s × ( s u m c [ n ] − s u m c [ j ] ) } f[i]=min\{f[j]+sumt[i] ×(sumc[i]-sumc[j])+s×(sumc[n]-sumc[j])\} f[i]=min{f[j]+sumt[i]×(sumc[i]−sumc[j])+s×(sumc[n]−sumc[j])} ( 0 ≤ j < i ) (0\leq j < i) (0≤j<i)进行编变形。
f [ i ] = f [ j ] + s u m t [ i ] × s u m c [ i ] − s u m t [ i ] × s u m c [ j ] + s × s u m c [ n ] − s × s u m c [ j ] f[i]=f[j]+sumt[i] ×sumc[i]-sumt[i]×sumc[j]+s×sumc[n]-s×sumc[j] f[i]=f[j]+sumt[i]×sumc[i]−sumt[i]×sumc[j]+s×sumc[n]−s×sumc[j]
f [ i ] = f [ j ] − s u m t [ i ] × s u m c [ j ] − s × s u m c [ j ] + s u m t [ i ] × s u m c [ i ] + s × s u m c [ n ] f[i]=f[j]-sumt[i]×sumc[j]-s×sumc[j]+sumt[i] ×sumc[i]+s×sumc[n] f[i]=f[j]−sumt[i]×sumc[j]−s×sumc[j]+sumt[i]×sumc[i]+s×sumc[n]
f [ i ] = f [ j ] − ( s u m t [ i ] + s ) × s u m c [ j ] + s u m t [ i ] × s u m c [ i ] + s × s u m c [ n ] f[i]=f[j]-(sumt[i]+s)×sumc[j]+sumt[i] ×sumc[i]+s×sumc[n] f[i]=f[j]−(sumt[i]+s)×sumc[j]+sumt[i]×sumc[i]+s×sumc[n]
移项得到
f [ j ] = ( s u m t [ i ] + s ) × s u m c [ j ] − s u m t [ i ] × s u m c [ i ] − s × s u m c [ n ] + f [ i ] f[j]=(sumt[i]+s)×sumc[j]-sumt[i] ×sumc[i]-s×sumc[n]+f[i] f[j]=(sumt[i]+s)×sumc[j]−sumt[i]×sumc[i]−s×sumc[n]+f[i]
上式是 y = k x + b y=kx+b y=kx+b的形式, y y y是 f [ j ] f[j] f[j], k k k是 ( s u m t [ i ] + s ) (sumt[i]+s) (sumt[i]+s), x x x是 s u m c [ j ] sumc[j] sumc[j], b b b是 f [ i ] − s u m t [ i ] × s u m c [ i ] − s × s u m c [ n ] f[i]-sumt[i] ×sumc[i]-s×sumc[n] f[i]−sumt[i]×sumc[i]−s×sumc[n]。
我们的目标是求 f [ i ] f[i] f[i]的最小值,因为 b b b中除了 f [ i ] f[i] f[i]以外的部分是常量,也正因此等价于去想办法让截距最小。因为 k k k也是一个常量, 所以本问题又可以转化为给定一条斜率固定的直线去找过一个 ( x , y ) (x,y) (x,y)点对,使得 b b b最小。 ( x , y ) (x,y) (x,y)点对有 ( s u m c [ 0 ] , f [ 0 ] ) (sumc[0],f[0]) (sumc[0],f[0]), ( s u m c [ 1 ] , f [ 1 ] ) (sumc[1],f[1]) (sumc[1],f[1]),…, ( s u m c [ i − 1 ] , f [ i − 1 ] ) (sumc[i-1],f[i-1]) (sumc[i−1],f[i−1])。
给出结论,无论斜率如何变化,最小值一定是取到凸包下边界的一个点。
具体来说,最小值一定是第一个大于直线斜率的线段头部 k i k_i ki的点。
分析题目:
1., k k k是 ( s u m t [ i ] + s ) (sumt[i]+s) (sumt[i]+s),单调递增。
2.新加入点的横坐标也是单调递增。
由于斜率 k k k是单调递增的,也就是说,如果当前的斜率 k k k大于队头两个点的斜率时,那么一开始的点就可以彻底删除,在以后也不会用到,所以凸包中的点可以用单调队列来维护。
维护一个凸包的做法:
1.查询的时候,把队头小于当前斜率k的点删掉。
f [ q [ h h + 1 ] − f [ q [ h h ] s u m c [ q [ h h + 1 ] ] − s u m c [ q [ h h ] ≤ s u m t [ i ] + s \frac{f[q[hh+1]-f[q[hh]}{sumc[q[hh+1]]-sumc[q[hh]}\leq sumt[i]+s sumc[q[hh+1]]−sumc[q[hh]f[q[hh+1]−f[q[hh]≤sumt[i]+s
2.插入的时候,把不在凸包上的点删掉。
f [ q [ t t ] − f [ q [ t t − 1 ] s u m c [ q [ h h ] ] − s u m c [ q [ h h − 1 ] ≥ f [ i ] − f [ q [ t t ] ] s u m c [ i ] − s u m c [ q [ h h ] ] \frac{f[q[tt]-f[q[tt-1]}{sumc[q[hh]]-sumc[q[hh-1]}\geq \frac{f[i]-f[q[tt]]}{sumc[i]-sumc[q[hh]]} sumc[q[hh]]−sumc[q[hh−1]f[q[tt]−f[q[tt−1]≥sumc[i]−sumc[q[hh]]f[i]−f[q[tt]]
时间复杂度为 O ( n ) O(n) O(n)
#include <iostream>
using namespace std;
typedef long long ll;
const int N = 300010;
int q[N];
ll t[N], c[N];
ll f[N];
int n, s;
int main()
{cin >> n >> s;for (int i = 1; i <= n; i ++ ){scanf("%lld%lld", &t[i], &c[i]);t[i] += t[i - 1];c[i] += c[i - 1];}int hh = 0, tt = 0;for (int i = 1; i <= n; i ++ ){while (hh < tt && f[q[hh + 1]] - f[q[hh]] <= (t[i] + s) * (c[q[hh + 1]] - c[q[hh]])) hh ++ ;int j = q[hh];f[i] = f[j] + t[i] * (c[i] - c[j]) + s * (c[n] - c[j]);while (hh < tt && (f[q[tt]] - f[q[tt - 1]]) * (c[i] - c[q[tt]]) >= (f[i] - f[q[tt]]) * (c[q[tt]] - c[q[tt - 1]])) tt -- ;q[++ tt] = i;}cout << f[n];return 0;
}
acwing302.任务安排3
和上一题不同的是, 本题中机器的工作时间可以为负数,也正因此斜率 k k k并不是随着 i i i单调递增的了,上一题中,对于凸包的头部和尾部均使用单调队列来处理,本题则需要使用二分去找到合适的点对,对尾部的处理同样使用单调队列。
#include <iostream>
using namespace std;
const int N = 300010;
typedef long long ll;
ll t[N], c[N];
ll f[N];
int q[N];
int n, s;
int main()
{cin >> n >> s;for (int i = 1; i <= n; i ++ ){scanf("%lld%lld", &t[i], &c[i]);t[i] += t[i - 1];c[i] += c[i - 1];}int hh = 0, tt = 0;for (int i = 1; i <= n; i ++ ){int l = hh, r = tt;while (l < r){int mid = l + r >> 1;if (f[q[mid + 1]] - f[q[mid]] > (double)(t[i] + s) * (c[q[mid + 1]] - c[q[mid]])) r = mid;else l = mid + 1;}int j = q[l];f[i] = f[j] - (t[i] + s) * c[j] + t[i] * c[i] + s * c[n];while (hh < tt && (double)(f[q[tt]] - f[q[tt - 1]]) * (c[i] - c[q[tt]]) >= (double)(f[i] - f[q[tt]]) * (c[q[tt]] - c[q[tt - 1]])) tt -- ;q[++ tt] = i;}cout << f[n];return 0;
}
acwing303.运输小猫
每一只小猫都会对应一个最早出发时间 a [ i ] = t [ i ] − d [ h [ i ] ] a[i]=t[i]-d[h[i]] a[i]=t[i]−d[h[i]],也就是结束玩耍的时间减去到1号山的距离。当我们处理完 a a a数组后,对数组 a a a进行一个从小打到的排序。这样一来,相邻一段猫肯定是要由一个饲养员接走的,饲养员的出发时间就是这一段最后一只猫对应的数组 a a a的值。
状态表示f[i][j]:
集合:对于前 i i i只猫,安排 j j j个饲养员去接猫的所有方案。
属性:min
状态计算:
f [ i ] [ j ] = m i n { f [ k ] [ j − 1 ] + ∑ k + 1 i ( a i − a u ) } f[i][j]=min\{f[k][j-1]+\sum_{k+1}^{i}(a_i-a_u)\} f[i][j]=min{f[k][j−1]+∑k+1i(ai−au)} ( 0 ≤ k < i ) \ \ \ (0\leq k <i) (0≤k<i)
f [ i ] [ j ] = m i n { f [ k ] [ j − 1 ] + ∑ k + 1 i a i − ∑ k + 1 i a u } f[i][j]=min\{f[k][j-1]+\sum_{k+1}^{i}a_i-\sum_{k+1}^{i}a_u\} f[i][j]=min{f[k][j−1]+∑k+1iai−∑k+1iau} ( 0 ≤ k < i ) \ \ \ (0\leq k <i) (0≤k<i)
f [ i ] [ j ] = m i n { f [ k ] [ j − 1 ] + ( i − k ) a i − ( s [ i ] − s [ k ] ) } f[i][j]=min\{f[k][j-1]+(i-k)a_i-(s[i]-s[k])\} f[i][j]=min{f[k][j−1]+(i−k)ai−(s[i]−s[k])} ( 0 ≤ k < i ) \ \ \ (0\leq k <i) (0≤k<i)
移项得:
f [ k ] [ j − 1 ] + s [ k ] = a [ i ] × k + f [ i ] [ j ] + s [ i ] − i a [ i ] f[k][j-1]+s[k]=a[i] ×k+f[i][j]+s[i]-ia[i] f[k][j−1]+s[k]=a[i]×k+f[i][j]+s[i]−ia[i]
至此,本题就转换为了任务安排2。
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
typedef long long ll;
const int N = 100010;
const int P = 110;
ll f[P][N];
ll a[N];
ll s[N];
int d[N];
int q[N];
int n, m, p;
ll get_y(int j, int k)
{return f[j - 1][k] + s[k];
}
int main()
{cin >> n >> m >> p;for (int i = 2; i <= n; i ++ ){scanf("%d", &d[i]);d[i] += d[i - 1];}for (int i = 1; i <= m; i ++ ){ll h, t;scanf("%lld%lld", &h, &t);a[i] = t - d[h];}sort(a + 1, a + m + 1);for (int i = 1; i <= m; i ++ ){s[i] = a[i];s[i] += s[i - 1];}memset(f,0x3f,sizeof f);for(int i = 0;i <= p;i ++)f[i][0] = 0;for (int i = 1; i <= p; i ++ ){int hh = 0, tt = 0;for (int j = 1; j <= m; j ++ ){while (hh < tt && get_y(i, q[hh + 1]) - get_y(i, q[hh]) <= (q[hh + 1] - q[hh]) * a[j]) hh ++;int k = q[hh];f[i][j] = f[i - 1][k] + (j - k) * a[j] - (s[j] - s[k]);while (hh < tt && (get_y(i, q[tt]) - get_y(i, q[tt - 1])) * (j - q[tt]) >= (get_y(i, j) - get_y(i, q[tt])) * (q[tt] - q[tt - 1])) tt --;q[++ tt] = j;}}cout << f[p][m];return 0;
}
相关文章:

动态规划——斜率优化DP
题目清单 acwing300.任务安排1 状态表示f[i]: 集合:完成前i个任务且第i个任务为最后一个批次最后一个任务的方案。 属性:min 状态计算: f [ i ] m i n { f [ j ] s u m t [ i ] ∑ j 1 i w [ u ] s ∑ j 1 n w [ i ] } f[i]min\{f[j…...

【深度之眼cs231n第七期】笔记(三十一)
目录 强化学习什么是强化学习?马尔可夫决策过程(MDP)Q-learning策略梯度SOTA深度强化学习 还剩一点小尾巴,还是把它写完吧。(距离我写下前面那行字又过了好几个月了【咸鱼本鱼】)(汗颜ÿ…...
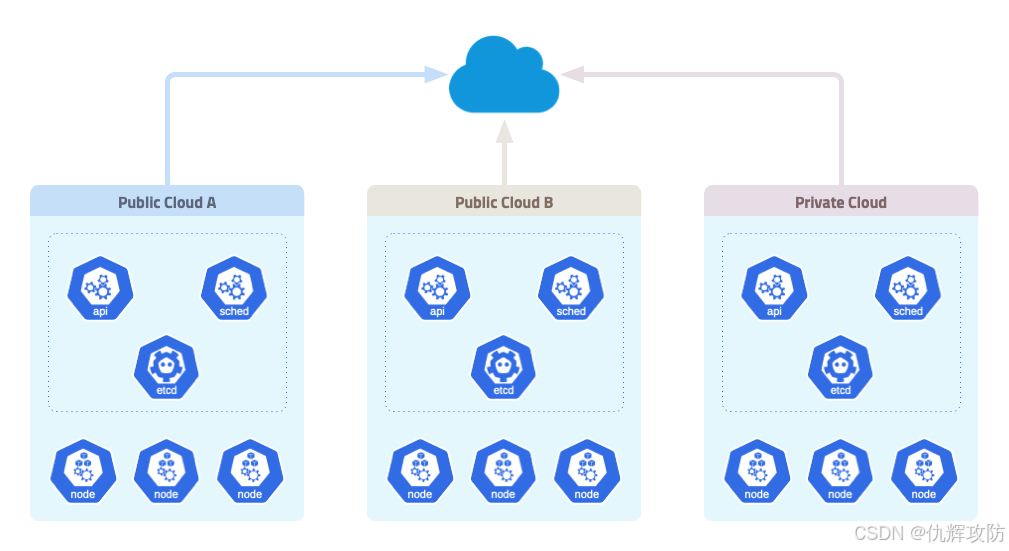
【云安全】云原生-K8S-简介
K8S简介 Kubernetes(简称K8S)是一种开源的容器编排平台,用于管理容器化应用的部署、扩展和运维。它由Google于2014年开源并交给CNCF(Cloud Native Computing Foundation)维护。K8S通过提供自动化、灵活的功能…...

SpringBoot中Excel表的导入、导出功能的实现
文章目录 一、easyExcel简介二、Excel表的导出2.1 添加 Maven 依赖2.2 创建导出数据的实体类4. 编写导出接口5. 前端代码6. 实现效果 三、excel表的导出1. Excel表导入的整体流程1.1 配置文件存储路径 2. 前端实现2.1 文件上传组件 2.2 文件上传逻辑3. 后端实现3.1 文件上传接口…...
)
Spark入门(Python)
目录 一、安装Spark 二、Spark基本操作 一、安装Spark pip3 install pyspark 二、Spark基本操作 # 导入spark的SparkContext,SparkConf模块 from pyspark import SparkContext, SparkConf # 导入os模块 import os # 设置PYSPARK的python环境 os.environ[PYSPARK_PYTHON] &…...

Daemon进程创建过程
Daemon创建过程: 1、fork,创建子进程。退出父进程。 2、setsid,创建新会话。脱离原会话、进程组、控制终端。 再次fork,与终端完全脱离。第二次fork的意义???? 先脱离原父进程&#…...

在sortablejs的拖拽排序情况下阻止input拖拽事件
如题 问题 在vue3的elementPlus的table中,通过sortablejs添加了行拖拽功能,但是在行内会有输入框,此时拖拽输入框会触发sortablejs的拖拽功能 解决 基于这个现象,我怀疑是由于拖拽事件未绑定而冒泡到后面的行上从而导致的拖拽…...

C++初阶—string类
第一章:为什么要学习string类 1.1 C语言中的字符串 C语言中,字符串是以\0结尾的一些字符的集合,为了操作方便,C标准库中提供了一些str系列的库函数,但是这些库函数与字符串是分离开的,不太符合OOP的思想&…...

C# 提取PDF表单数据
目录 使用工具 C# 提取多个PDF表单域的数据 C# 提取特定PDF表单域的数据 PDF表单是一种常见的数据收集工具,广泛应用于调查问卷、业务合同等场景。凭借出色的跨平台兼容性和标准化特点,PDF表单在各行各业中得到了广泛应用。然而,当需要整合…...

算法刷题Day28:BM66 最长公共子串
题目链接,点击跳转 题目描述: 解题思路: 方法一:暴力枚举 遍历str1的每个字符x,并在str2中寻找以相同元素x为起始的最长字符串。记录最长的公共子串及其长度。 代码实现: def LCS(self, str1: str, st…...
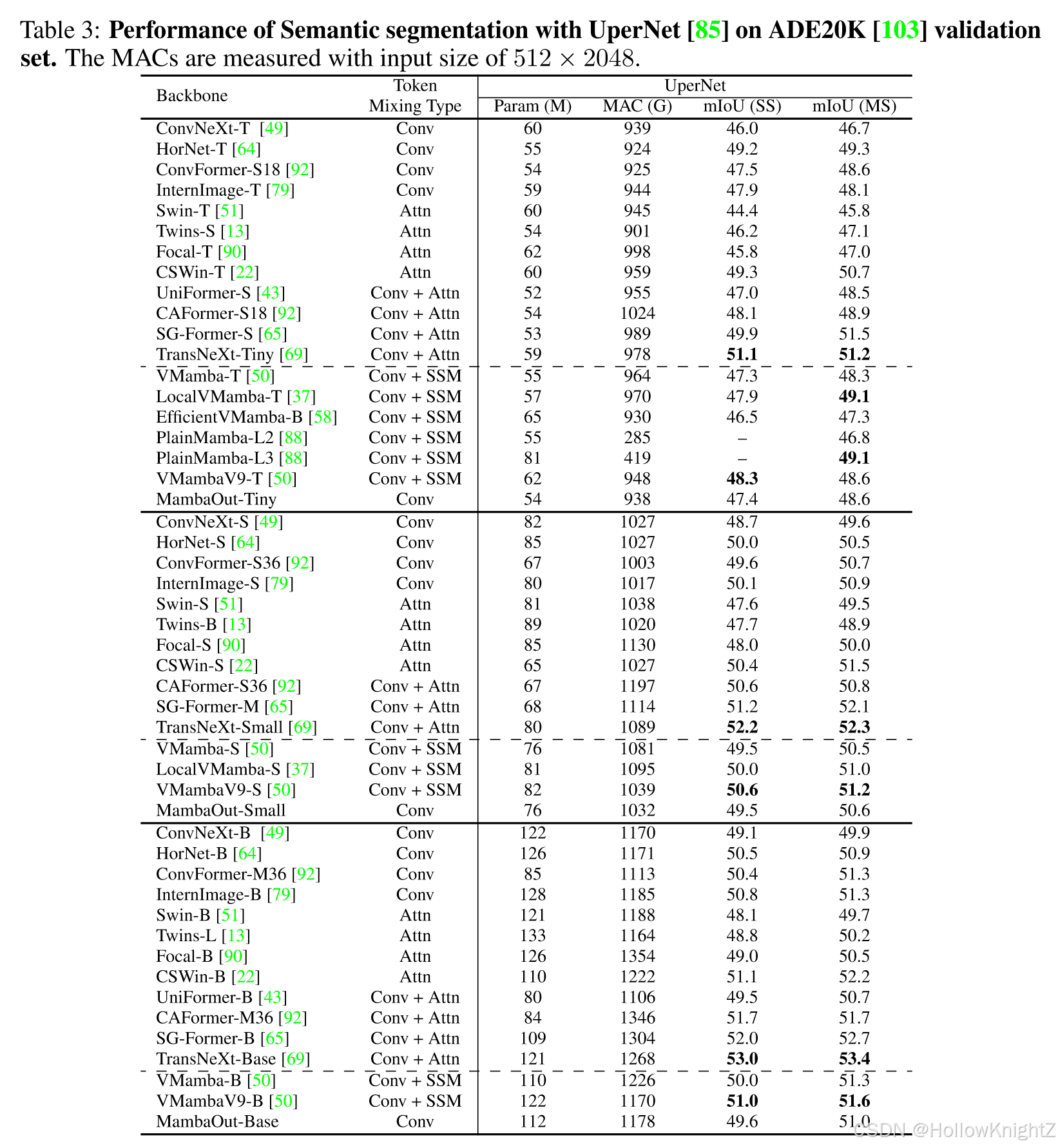
论文阅读笔记:MambaOut: Do We Really Need Mamba for Vision?
论文阅读笔记:MambaOut: Do We Really Need Mamba for Vision? 1 背景2 创新点3 方法4 模块4.1 Mamba适合什么任务4.2 视觉识别任务是否有很长的序列4.3 视觉任务是否需要因果token混合模式4.4 关于Mamba对于视觉的必要性假设 5 效果 论文:https://arxi…...
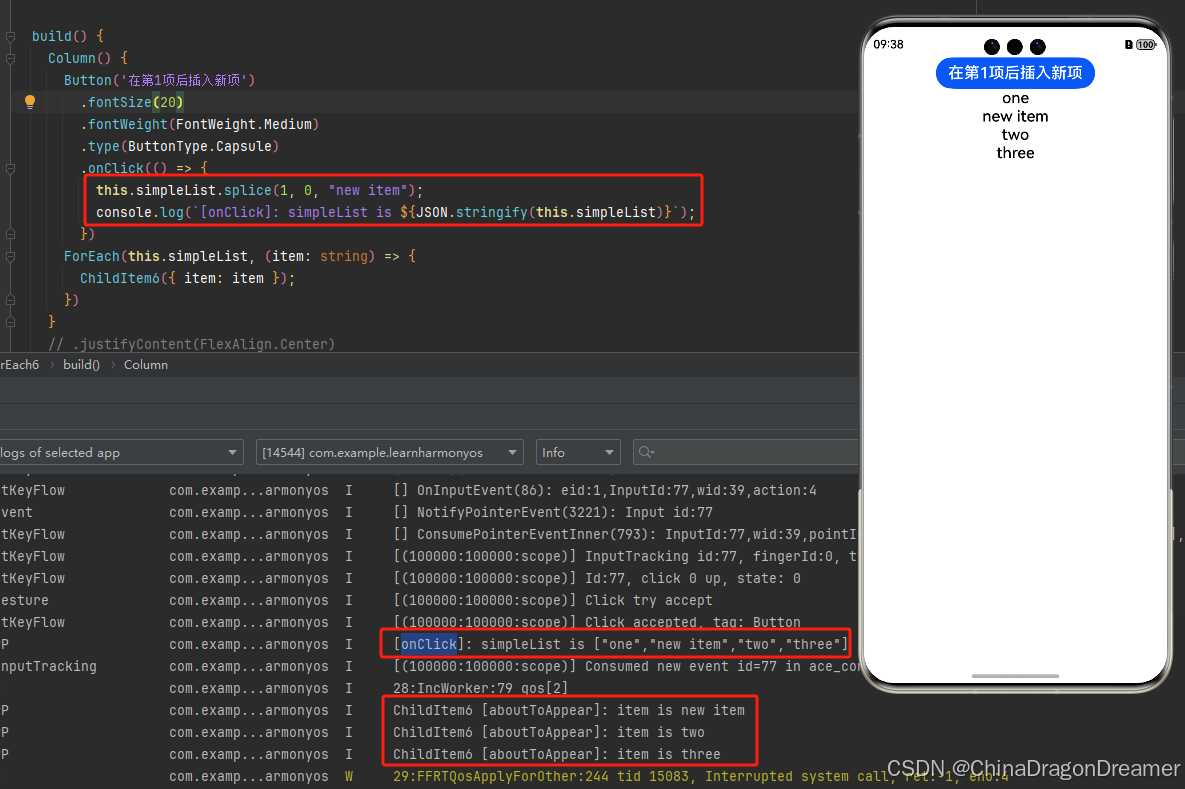
HarmonyOS:ForEach:循环渲染
一、前言 ForEach接口基于数组类型数据来进行循环渲染,需要与容器组件配合使用,且接口返回的组件应当是允许包含在ForEach父容器组件中的子组件。例如,ListItem组件要求ForEach的父容器组件必须为List组件。 API参数说明见:ForEa…...

Python3 【函数】项目实战:5 个新颖的学习案例
Python3 【函数】项目实战:5 个新颖的学习案例 本文包含5编程学习案例,具体项目如下: 简易聊天机器人待办事项提醒器密码生成器简易文本分析工具简易文件加密解密工具 项目 1:简易聊天机器人 功能描述: 实现一个简易…...

XSS 漏洞全面解析:原理、危害与防范
目录 前言编辑 漏洞原理 XSS 漏洞的危害 检测 XSS 漏洞的方法 防范 XSS 漏洞的措施 前言 在网络安全的复杂版图中,XSS 漏洞,即跨站脚本攻击(Cross - Site Scripting),是一类极为普遍且威胁巨大的安全隐患。随着互…...

从 GShard 到 DeepSeek-V3:回顾 MoE 大模型负载均衡策略演进
作者:小天狼星不来客 原文:https://zhuanlan.zhihu.com/p/19117825360 故事要从 GShard 说起——当时,人们意识到拥有数十亿甚至数万亿参数的模型可以通过某种形式的“稀疏化(sparsified)”来在保持高精度的同时加速训…...

【回溯+剪枝】回溯算法的概念 全排列问题
文章目录 46. 全排列Ⅰ. 什么是回溯算法❓❓❓Ⅱ. 回溯算法的应用1、组合问题2、排列问题3、子集问题 Ⅲ. 解题思路:回溯 剪枝 46. 全排列 46. 全排列 给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。 …...

Flutter解决macbook M芯片Android Studio中不显示IOS真机的问题
下载了最新的Android Studio LadyBug 下载了最新的xcode16.2 结果,只有安卓真机才在Android studio显示, IOS真机只在xcode显示 IOS真机不在android studio显示。 解决方法是: 在终端运行如下命令: sudo xcode-select -s /Applic…...

自签证书的dockerfile中from命令无法拉取镜像而docker的pull命令能拉取镜像
问题现象: docker pull images拉取镜像正常 dockerfile中的from命令拉取镜像就会报出证书错误。报错信息如下: [bjxtbwj-kvm-test-jenkins-6-243 ceshi_dockerfile]$ docker build . [] Building 0.4s (3/3) FINISHED …...

【MySQL】--- 复合查询 内外连接
Welcome to 9ilks Code World (๑•́ ₃ •̀๑) 个人主页: 9ilk (๑•́ ₃ •̀๑) 文章专栏: MySQL 🏠 基本查询回顾 假设有以下表结构: 查询工资高于500或岗位为MANAGER的雇员,同时还要满足他们的姓名首字母为…...

QT TLS initialization failed
qt使用QNetworkAccessManager下载文件(给出的链接可以在浏览器里面下载文件),下载失败, 提示“TLS initialization failed”通常是由于Qt在使用HTTPS进行文件下载时,未能正确初始化TLS(安全传输层协议&…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

uniapp 实现腾讯云IM群文件上传下载功能
UniApp 集成腾讯云IM实现群文件上传下载功能全攻略 一、功能背景与技术选型 在团队协作场景中,群文件共享是核心需求之一。本文将介绍如何基于腾讯云IMCOS,在uniapp中实现: 群内文件上传/下载文件元数据管理下载进度追踪跨平台文件预览 二…...
