数据结构与算法再探(六)动态规划
目录
动态规划 (Dynamic Programming, DP)
动态规划的基本思想
动态规划的核心概念
动态规划的实现步骤
动态规划实例
1、爬楼梯
c++ 递归(超时)需要使用记忆化递归
循环
2、打家劫舍
3、最小路径和
4、完全平方数
5、最长公共子序列
6、0-1背包问题
总结
动态规划 (Dynamic Programming, DP)
释义:动态规划是一种解决复杂问题的优化方法,通过将大问题拆解成小问题,逐步解决小问题,最终得到大问题的解。它通常用于求解具有最优子结构和重构子问题的优化问题。C++中的动态规划算法应用广泛,尤其是在最短路径、背包问题、最长公共子序列、矩阵链乘法等领域。
动态规划的基本思想
动态规划方法通过建立状态转移方程(recurrence relation)来表示问题的子问题之间的关系。每个子问题的解只计算一次,然后保存起来避免重复计算,从而达到减少计算量的目的。常见的动态规划问题通常可以通过两种方式实现:自顶向下的递归(带记忆化)和自底向上的迭代。
动态规划的核心概念
| 最优子结构 | 问题的最优解可以通过子问题的最优解得到。换句话说问题的最优解包含了子问题的最优解 |
| 重叠子问题 | 问题可以被分解成多个子问题,且这些子问题在计算过程中会被多次求解。 |
| 状态转移方程 | 动态规划的核心是通过状态转移方程将大问题分解为小问题,进而通过小问题的解推导出大问题的解 |
动态规划的实现步骤
| 定义状态 | 首先定义子问题的状态。通常状态的定义取决于问题的具体性质。例如,在最短路径问题中,可以定义状态为当前节点到起点的最短路径长度 |
| 初始化状态 | 为状态的初值赋值。通常,某些边界条件会初始化为已知值。 |
| 状态转移方程 | 根据问题的性质,推导出状态转移方程,描述如何从当前状态推导到下一个状态 |
| 计算最优解 | 根据状态转移方程,从最简单的子问题开始逐步计算,直到得到最终问题的解 |
| 结果回溯(如果需要) | :如果问题要求返回具体的解路径(例如路径、序列等),则需要在求解过程中保存路径信息,最后回溯得到结果 |
动态规划实例
1、爬楼梯
70. 爬楼梯 - 力扣(LeetCode)
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢
状态定义:dp[i]表示爬到第 i 阶楼梯的不同方法数。
状态转移方程:dp[i] =dp[i-1]+dp[i-2],即爬到第 i 阶楼梯可以从第 i-1 阶或第 i-2 阶跳跃过来。
为什么 d[i] = d[i-1] + d[i-2] 不会重复包含 d[i-2]?
在动态规划中,d[i] 表示到达第 i 阶楼梯的总方法数。当计算 d[i] 时,d[i-1] 和 d[i-2] 分别表示到达第 i-1 阶和第 i-2 阶楼梯的方法数。这两个数并没有交叉或重复计算的部分,它们分别独立表示从不同阶梯出发的跳跃方式。更具体的解释:d[i-1] 代表的是从第 i-1 阶楼梯跳一步到达第 i 阶楼梯的方法数。d[i-2] 代表的是从第 i-2 阶楼梯跳两步到达第 i 阶楼梯的方法数。
这两个值分别代表不同的跳跃方式:从 i-1 到 i 是一次跳跃,跳跃的过程中,不需要考虑 i-2。
从 i-2 到 i 是两次跳跃,这一步也不会再次涉及到 i-1。
因此,d[i-1] 和 d[i-2] 并没有重叠,它们分别计算的是不同的路径,最终的 d[i] = d[i-1] + d[i-2] 是将这两条路径相加,得到的总方法数。
c++ 递归(超时)需要使用记忆化递归
class Solution {
public:int climbStairs(int n) {if(n<=2) return n;return climbStairs(n-1)+climbStairs(n-2);}
};//记录搜素值
vector<int> res;
int dfs(int i){if(i<=1){return 1;}if(res[i]){return res[i];}return res[i]=dfs(i-1)+dfs(i-2);
}循环
int climbStairs(int n) {if (n <= 2)return n;vector<int> dp(n + 1, 1);for (int i = 2; i <= n; ++i) {dp[i] = dp[i - 1] + dp[i - 2];}return dp[n];}//空间优化int climbStairs(int n) {if (n <= 2)return n;int pre2 = 1, pre1 = 2, cur;for (int i = 2; i < n; ++i) {cur = pre1 + pre2;pre2 = pre1;pre1 = cur;}return cur;}2、打家劫舍
198. 打家劫舍 - 力扣(LeetCode)
一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。给定一个代表每个房屋存放金额的非负整数数组,计算你 不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。
设 dp[i] 表示偷窃前 i 家房子时的最大金额。显然,对于每个房子,存在两个选择:偷窃第 i 家房子:如果你偷窃第 i 家房子,那么你不能偷窃第 i-1 家房子,因此最大金额是 dp[i-2] + nums[i],其中 nums[i] 表示第 i 家房子的金额。
不偷窃第 i 家房子:那么最大金额就是 dp[i-1],即偷窃前 i-1 家房子时的最大金额。因此,递推关系式为:dp[i]=max(dp[i−1],dp[i−2]+nums[i])其中,dp[0] 为偷窃第一家房子的金额,dp[1] 为偷窃前两家房子时的最大金额。
状态转移:dp[i] = max(dp[i-1], dp[i-2] + nums[i])
初始状态:dp[0] = nums[0],dp[1] = max(nums[0], nums[1])。
int rob(vector<int>& nums) {int n=nums.size();vector<int> dp(n,0);if(n==1){return nums[0];}dp[0]=nums[0];dp[1]=max(nums[0],nums[1]);for(int i=2;i<n;++i){dp[i]=max(dp[i-1],dp[i-2]+nums[i]);}return dp[n-1];}
//空间优化int rob(vector<int>& nums) {int n=nums.size();//vector<int> dp(n,0);if(n==1){return nums[0];}auto pre=0;auto cur=0;int res=0;for(int i=0;i<n;++i){res=max(cur,pre+nums[i]);pre=cur;cur=res;}return res;}3、最小路径和
64. 最小路径和 - 力扣(LeetCode)
给定一个包含非负整数的 m x n 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
状态定义:用 dp[i][j] 表示到达位置 (i, j) 的最小路径和。
状态转移:从上方到达 (i, j) 的路径和为 dp[i-1][j] + grid[i][j]。从左方到达 (i, j) 的路径和为 dp[i][j-1] + grid[i][j]。因此,状态转移方程为:dp[i][j]=min(dp[i−1][j],dp[i][j−1])+grid[i][j];其中,dp[i-1][j] 和 dp[i][j-1] 分别表示到达上方和左方的最小路径和。
初始状态:dp[0][0] = grid[0][0],即起点的值。第一行和第一列的值需要单独处理,因为它们只能从一个方向到达:第一行:dp[0][j] = dp[0][j-1] + grid[0][j];第一列:dp[i][0] = dp[i-1][0] + grid[i][0]
返回结果:最终的结果为 dp[m-1][n-1],即到达右下角的最小路径和。
class Solution {
public:int minPathSum(vector<vector<int>>& grid) {int m=grid.size();int n=grid[0].size();vector<vector<int>> dp(m,vector<int>(n,0));for(int i=0;i<m;++i){for(int j=0;j<n;++j){if(i==0&&j==0){dp[i][j]=grid[i][j];}else if(i==0){dp[i][j]=dp[i][j-1]+grid[i][j];}else if(j==0){dp[i][j]=dp[i-1][j]+grid[i][j];}else{dp[i][j]=min(dp[i-1][j],dp[i][j-1])+grid[i][j];}}}return dp[m-1][n-1];}
};4、完全平方数
279. 完全平方数 - 力扣(LeetCode)
给你一个整数 n ,返回 和为 n 的完全平方数的最少数量。完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。
状态定义:用 dp[i] 表示和为 i 的最小完全平方数的数量。
状态转移:对于每个 i,我们可以尝试用每个小于等于 i 的完全平方数 j*j 来更新 dp[i]:dp[i]=min(dp[i],dp[i−j∗j]+1), 其中 j 是从 1 到 \sqrt{i} 的整数(位置 i 只依赖 i - j*j 的位置,如 i - 1、 i - 4、 i - 9 等等,才能满足完全平方分割的条件)。
初始状态:dp[0] = 0,表示和为 0 时不需要任何数。
class Solution {
public:int numSquares(int n) {vector<int> dp(n+1,INT_MAX);dp[0]=0;for(int i=1;i<=n;++i){for(int j=1;j*j<=i;++j){dp[i]=min(dp[i],dp[i-j*j]+1);}}return dp[n];}
};5、最长公共子序列
1143. 最长公共子序列 - 力扣(LeetCode)
给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ,返回 0 。一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。例如,"ace" 是 "abcde" 的子序列,但 "aec" 不是 "abcde" 的子序列。
状态定义:用 dp[i][j] 表示 text1 的前 i 个字符与 text2 的前 j 个字符的最长公共子序列的长度。
状态转移:如果 text1[i-1] == text2[j-1],那么 dp[i][j] = dp[i-1][j-1] + 1,表示当前字符相等时,公共子序列长度加一。如果 text1[i-1] != text2[j-1],那么 dp[i][j] = \max(dp[i-1][j], dp[i][j-1]),表示当前字符不相等时,最长公共子序列的长度为去掉当前字符后的最大值。
初始状态:dp[0][j] = 0 和 dp[i][0] = 0,表示任意一个字符串为空时,公共子序列长度为 0。
返回结果:最终的结果为 dp[m][n],其中 m 和 n 分别是 text1 和 text2 的长度。
class Solution {
public:int longestCommonSubsequence(string text1, string text2) {int m = text1.length(), n = text2.length();vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));for (int i = 1; i <= m; ++i) {for (int j = 1; j <= n; ++j) {if (text1[i - 1] == text2[j - 1]) {dp[i][j] = dp[i - 1][j - 1] + 1;} else {dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);}}}return dp[m][n];}
};6、0-1背包问题
有 n 个物品,每个物品 i 有一个重量 weights[i] 和一个价值 values[i]。背包的最大容量为 W。需要找到一个选择方案,使得所选物品的总重量不超过 W,并且总价值最大。动态规划的思路
状态定义:用 dp[i][j] 表示前 i 个物品中,能够放入容量为 j 的背包的最大价值。
状态转移:如果不选择第 i 个物品,最大价值为 dp[i-1][j]。如果选择第 i 个物品,最大价值为 values[i-1] + dp[i-1][j-weights[i-1]](前提是 j 大于等于 weights[i-1])。
因此,状态转移方程为:dp[i][j]=max(dp[i−1][j],values[i−1]+dp[i−1][j−weights[i−1]])if j≥weights[i−1]初始状态:dp[0][j] = 0,表示没有物品时,最大价值为 0。返回结果:最终的结果为 dp[n][W],即使用所有物品时,背包容量为 W 的最大价值。
int knapsack(vector<int> weights, vector<int> values, int N, int W)
{vector<vector<int>> dp(N + 1, vector<int>(W + 1, 0));for (int i = 1; i <= N; ++i){int w = weights[i - 1], v = values[i - 1];for (int j = 1; j <= W; ++j){if (j >= w){dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w] + v);}else{dp[i][j] = dp[i - 1][j];}}}return dp[N][W];
}总结
动态规划是一种强大的方法,可以解决很多最优化问题。其核心思想是将问题拆解为子问题,通过记忆化或迭代的方式避免重复计算,从而提高效率。在C++中,动态规划的实现通常涉及状态定义、状态转移方程的推导以及最终解的计算。通过具体的算法问题(如背包问题、最长公共子序列、爬楼梯问题等)来理解和应用动态规划,可以帮助解决复杂的优化问题。
相关文章:
动态规划)
数据结构与算法再探(六)动态规划
目录 动态规划 (Dynamic Programming, DP) 动态规划的基本思想 动态规划的核心概念 动态规划的实现步骤 动态规划实例 1、爬楼梯 c 递归(超时)需要使用记忆化递归 循环 2、打家劫舍 3、最小路径和 4、完全平方数 5、最长公共子序列 6、0-1背…...
若依基本使用及改造记录
若依框架想必大家都了解得不少,不可否认这是一款及其简便易用的框架。 在某种情况下(比如私活)使用起来可谓是快得一匹。 在这里小兵结合自身实际使用情况,记录一下我对若依框架的使用和改造情况。 一、源码下载 前往码云进行…...

学习数据结构(2)空间复杂度+顺序表
1.空间复杂度 (1)概念 空间复杂度也是一个数学表达式,表示一个算法在运行过程中根据算法的需要额外临时开辟的空间。 空间复杂度不是指程序占用了多少bytes的空间,因为常规情况每个对象大小差异不会很大,所以空间复杂…...

C语言复习
1.进制 三要素:数位(第几位) 基数 位权(当前位对应的值) 二进制:B 八进制:O 十进制:D 十六进制:X 0和1 111 /072 10 …...

Qt监控系统辅屏预览/可以同时打开4个屏幕预览/支持5x64通道预览/onvif和rtsp接入/性能好
一、前言说明 在监控系统中,一般主界面肯定带了多个通道比如16/64通道的画面预览,随着电脑性能的增强和多屏幕的发展,再加上现在监控摄像头数量的增加,越来越多的用户希望在不同的屏幕预览不同的实时画面,一个办法是打…...
ubuntu22安装issac gym记录
整体参考:https://blog.csdn.net/Yakusha/article/details/144306858 安装完成后的整体版本信息 ubuntu:22.04内核:6.8.0-51-generic显卡:NVIDIA GeForce RTX 3050 OEM显卡驱动:535.216.03cuda:12.2cudnn&…...
IDEA工具下载、配置和Tomcat配置
1. IDEA工具下载、配置 1.1. IDEA工具下载 1.1.1. 下载方式一 官方地址下载 1.1.2. 下载方式二 官方地址下载:https://www.jetbrains.com/idea/ 1.1.3. 注册账户 官网地址:https://account.jetbrains.com/login 1.1.4. JetBrains官方账号注册…...
Three.js实战项目02:vue3+three.js实现汽车展厅项目
文章目录 实战项目02项目预览项目创建初始化项目模型加载与展厅灯光加载汽车模型设置灯光材质设置完整项目下载实战项目02 项目预览 完整项目效果: 项目创建 创建项目: pnpm create vue安装包: pnpm add three@0.153.0 pnpm add gsap初始化项目 修改App.js代码&#x…...
动态规划——斜率优化DP
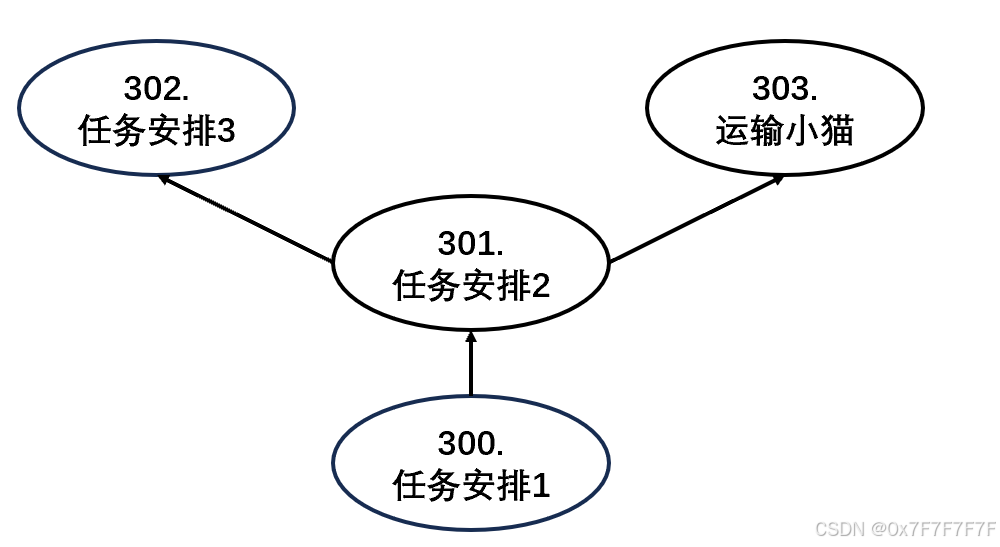
题目清单 acwing300.任务安排1 状态表示f[i]: 集合:完成前i个任务且第i个任务为最后一个批次最后一个任务的方案。 属性:min 状态计算: f [ i ] m i n { f [ j ] s u m t [ i ] ∑ j 1 i w [ u ] s ∑ j 1 n w [ i ] } f[i]min\{f[j…...

【深度之眼cs231n第七期】笔记(三十一)
目录 强化学习什么是强化学习?马尔可夫决策过程(MDP)Q-learning策略梯度SOTA深度强化学习 还剩一点小尾巴,还是把它写完吧。(距离我写下前面那行字又过了好几个月了【咸鱼本鱼】)(汗颜ÿ…...
【云安全】云原生-K8S-简介
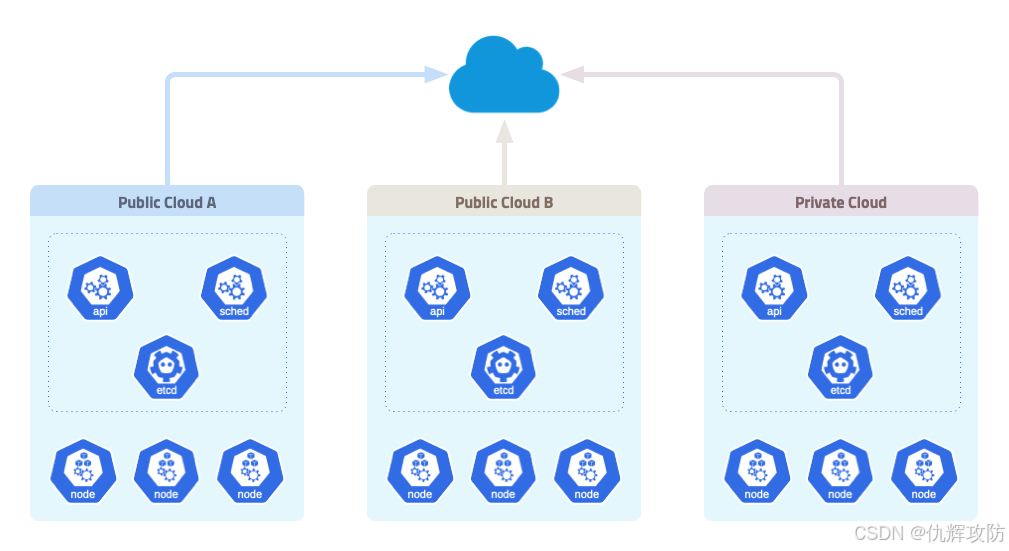
K8S简介 Kubernetes(简称K8S)是一种开源的容器编排平台,用于管理容器化应用的部署、扩展和运维。它由Google于2014年开源并交给CNCF(Cloud Native Computing Foundation)维护。K8S通过提供自动化、灵活的功能…...

SpringBoot中Excel表的导入、导出功能的实现
文章目录 一、easyExcel简介二、Excel表的导出2.1 添加 Maven 依赖2.2 创建导出数据的实体类4. 编写导出接口5. 前端代码6. 实现效果 三、excel表的导出1. Excel表导入的整体流程1.1 配置文件存储路径 2. 前端实现2.1 文件上传组件 2.2 文件上传逻辑3. 后端实现3.1 文件上传接口…...
)
Spark入门(Python)
目录 一、安装Spark 二、Spark基本操作 一、安装Spark pip3 install pyspark 二、Spark基本操作 # 导入spark的SparkContext,SparkConf模块 from pyspark import SparkContext, SparkConf # 导入os模块 import os # 设置PYSPARK的python环境 os.environ[PYSPARK_PYTHON] &…...

Daemon进程创建过程
Daemon创建过程: 1、fork,创建子进程。退出父进程。 2、setsid,创建新会话。脱离原会话、进程组、控制终端。 再次fork,与终端完全脱离。第二次fork的意义???? 先脱离原父进程&#…...

在sortablejs的拖拽排序情况下阻止input拖拽事件
如题 问题 在vue3的elementPlus的table中,通过sortablejs添加了行拖拽功能,但是在行内会有输入框,此时拖拽输入框会触发sortablejs的拖拽功能 解决 基于这个现象,我怀疑是由于拖拽事件未绑定而冒泡到后面的行上从而导致的拖拽…...

C++初阶—string类
第一章:为什么要学习string类 1.1 C语言中的字符串 C语言中,字符串是以\0结尾的一些字符的集合,为了操作方便,C标准库中提供了一些str系列的库函数,但是这些库函数与字符串是分离开的,不太符合OOP的思想&…...

C# 提取PDF表单数据
目录 使用工具 C# 提取多个PDF表单域的数据 C# 提取特定PDF表单域的数据 PDF表单是一种常见的数据收集工具,广泛应用于调查问卷、业务合同等场景。凭借出色的跨平台兼容性和标准化特点,PDF表单在各行各业中得到了广泛应用。然而,当需要整合…...

算法刷题Day28:BM66 最长公共子串
题目链接,点击跳转 题目描述: 解题思路: 方法一:暴力枚举 遍历str1的每个字符x,并在str2中寻找以相同元素x为起始的最长字符串。记录最长的公共子串及其长度。 代码实现: def LCS(self, str1: str, st…...
论文阅读笔记:MambaOut: Do We Really Need Mamba for Vision?
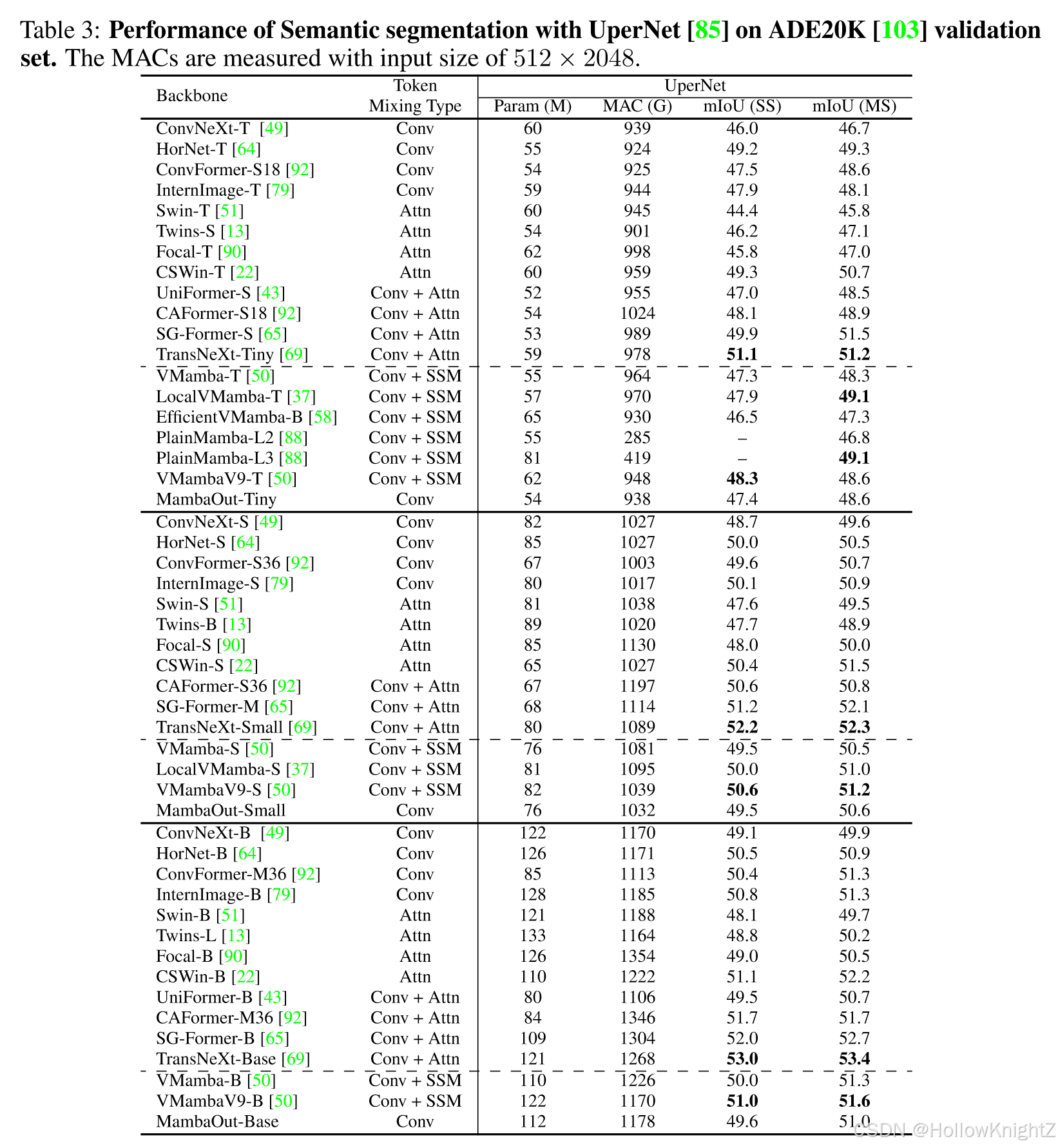
论文阅读笔记:MambaOut: Do We Really Need Mamba for Vision? 1 背景2 创新点3 方法4 模块4.1 Mamba适合什么任务4.2 视觉识别任务是否有很长的序列4.3 视觉任务是否需要因果token混合模式4.4 关于Mamba对于视觉的必要性假设 5 效果 论文:https://arxi…...
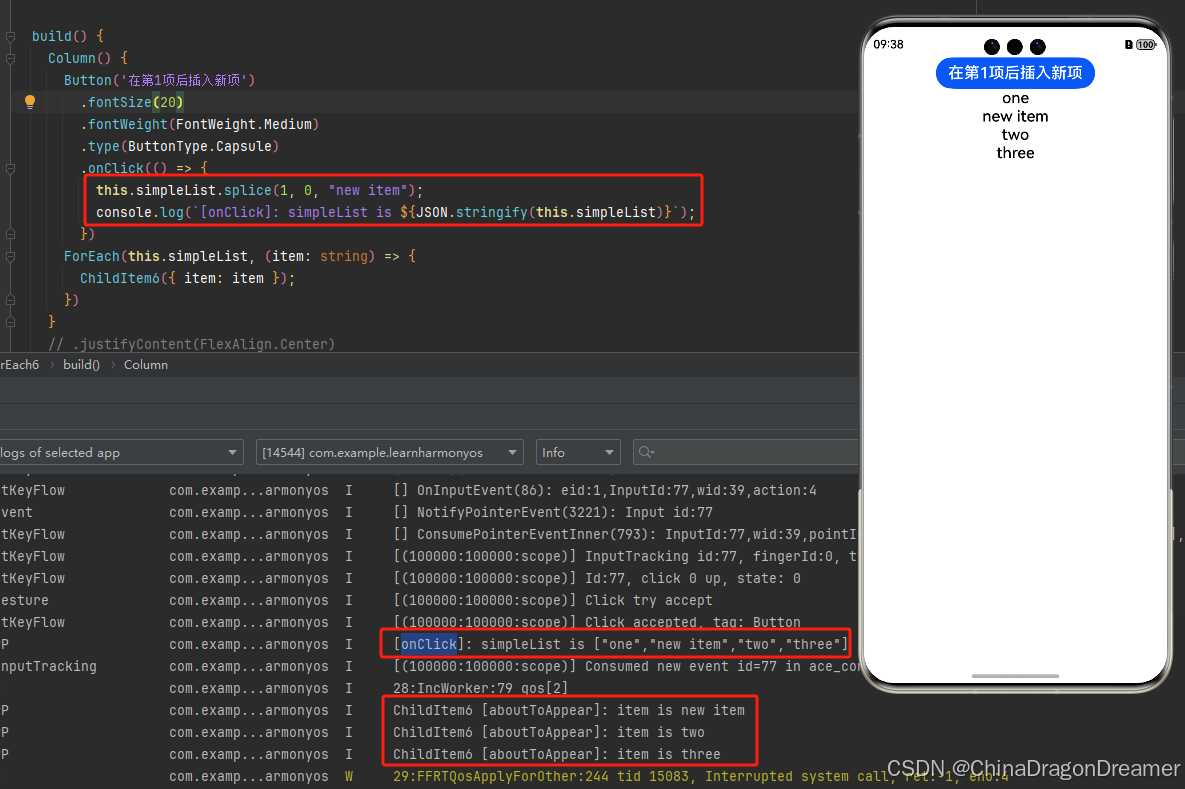
HarmonyOS:ForEach:循环渲染
一、前言 ForEach接口基于数组类型数据来进行循环渲染,需要与容器组件配合使用,且接口返回的组件应当是允许包含在ForEach父容器组件中的子组件。例如,ListItem组件要求ForEach的父容器组件必须为List组件。 API参数说明见:ForEa…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...
