python:洛伦兹变换
洛伦兹变换(Lorentz transformations)是相对论中的一个重要概念,特别是在讨论时空的变换时非常重要。在四维时空的背景下,洛伦兹变换描述了在不同惯性参考系之间如何变换时间和空间坐标。在狭义相对论中,洛伦兹变换通常指的是洛伦兹群(Lorentz group)所描述的变换,它包括了平移(boosts)和旋转(rotations)。
洛伦兹变换的数学形式
在四维闵可夫斯基空间中,一个事件可以用一个四维向量$(t, x, y, z)$来表示,其中$t$是时间坐标,而$x, y, z$是空间坐标。洛伦兹变换可以用一个四维旋转矩阵$L$表示,该矩阵满足:
$$ L^T J L = J $$
其中,$J$是四维闵可夫斯基度规矩阵,定义为:
$$ J = \begin{pmatrix} 1 & 0 & 0 & 0 \ 0 & -1 & 0 & 0 \ 0 & 0 & -1 & 0 \ 0 & 0 & 0 & -1 \end{pmatrix} $$
洛伦兹变换的性质
-
保持光速不变:洛伦兹变换保持光速不变,即任何惯性参考系中的光速都是常数。
-
时空的相对性:在不同的惯性参考系中,时间和空间坐标的测量值会不同,但物理定律的形式不变。
在Python中的实现
虽然Python不是专门为数学或物理计算设计的语言(如MATLAB或Mathematica),但你可以使用numpy库来处理洛伦兹变换。下面是一个简单的例子,展示如何使用 numpy 来实现一个基本的洛伦兹变换:
# -*- coding: utf-8 -*-
""" 示例:计算一个简单的洛伦兹变换 """
import numpy as np# 定义洛伦兹变换矩阵
def lorentz_matrix(beta_x, beta_y, beta_z):gamma = 1 / np.sqrt(1 - beta_x**2 - beta_y**2 - beta_z**2)L = np.array([[gamma, -gamma*beta_x, -gamma*beta_y, -gamma*beta_z],[-gamma*beta_x, 1 + (gamma-1)*beta_x**2, (gamma-1)*beta_x*beta_y, (gamma-1)*beta_x*beta_z],[-gamma*beta_y, (gamma-1)*beta_x*beta_y, 1 + (gamma-1)*beta_y**2, (gamma-1)*beta_y*beta_z],[-gamma*beta_z, (gamma-1)*beta_x*beta_z, (gamma-1)*beta_y*beta_z, 1 + (gamma-1)*beta_z**2]])return L# x方向的速度分量(相对于光速c的比例)
beta_x = 0.5
L = lorentz_matrix(beta_x, 0, 0)
print(" 洛伦兹变换矩阵:\n", L)
运行 python test_lorentz.py
推荐阅读:python:斐索实验(Fizeau experiment)
参阅:Edward Norton Lorenz
在相对论中,洛伦兹变换(Lorentz Transformation)是描述两个惯性参考系之间时空坐标的变换关系。洛伦兹变换是狭义相对论的核心内容之一,它取代了经典力学中的伽利略变换,用于处理高速运动下的物理现象。
在Python中,我们可以使用NumPy库来实现洛伦兹变换。以下是一个简单的示例 test_lorentz1.py
import numpy as npdef lorentz_transformation(v, x, t):"""计算洛伦兹变换:param v: 相对速度 (单位: c, 光速):param x: 空间坐标 (单位: 米):param t: 时间坐标 (单位: 秒):return: 变换后的空间坐标 x' 和时间坐标 t'"""c = 1 # 光速归一化gamma = 1 / np.sqrt(1 - v**2 / c**2) # 洛伦兹因子# 洛伦兹变换公式x_prime = gamma * (x - v * t)t_prime = gamma * (t - v * x / c**2)return x_prime, t_prime# 示例参数
v = 0.8 # 相对速度 (0.8c)
x = 10 # 空间坐标 (10 米)
t = 5 # 时间坐标 (5 秒)# 计算洛伦兹变换
x_prime, t_prime = lorentz_transformation(v, x, t)print(f"变换后的空间坐标 x': {x_prime} 米")
print(f"变换后的时间坐标 t': {t_prime} 秒")
解释
-
洛伦兹因子 (gamma): 这是洛伦兹变换中的一个关键参数,定义为
gamma = 1 / sqrt(1 - v^2 / c^2),其中v是相对速度,c是光速。 -
洛伦兹变换公式:
-
x' = gamma * (x - v * t) -
t' = gamma * (t - v * x / c^2)
-
输出
运行上述代码后,你将得到变换后的空间坐标 x' 和时间坐标 t'。
注意事项
-
在相对论中,速度
v通常以光速c为单位,因此v的取值范围是0 <= v < 1。 -
代码中的光速
c被归一化为1,因此速度v也是以光速为单位。
这个示例展示了如何使用Python计算洛伦兹变换,你可以根据需要修改参数或扩展代码。
在相对论中,洛伦兹变换(Lorentz transformation)是一个非常重要的概念,它描述了不同惯性参考系之间的时空坐标变换关系。下面为你详细介绍如何使用 Python 来实现洛伦兹变换。
编写 test_lorenz.py 如下
# -*- coding: utf-8 -*-
""" 示例:计算正v逆的洛伦兹变换 """
import numpy as np
import math# 定义真空中的光速
c = 299792458 # 单位:米/秒def lorentz_factor(v):"""计算洛伦兹因子:param v: 相对速度:return: 洛伦兹因子"""return 1 / math.sqrt(1 - (v**2 / c**2))def lorentz_transform(t, x, v):"""进行洛伦兹正变换:param t: 原参考系中的时间:param x: 原参考系中的位置:param v: 相对速度:return: 变换后参考系中的时间和位置"""gamma = lorentz_factor(v)t_prime = gamma * (t - (v * x) / (c**2))x_prime = gamma * (x - v * t)return t_prime, x_primedef inverse_lorentz_transform(t_prime, x_prime, v):"""进行洛伦兹逆变换:param t_prime: 变换后参考系中的时间:param x_prime: 变换后参考系中的位置:param v: 相对速度:return: 原参考系中的时间和位置"""gamma = lorentz_factor(v)t = gamma * (t_prime + (v * x_prime) / (c**2))x = gamma * (x_prime + v * t_prime)return t, x# 示例使用
# 原参考系中的时空坐标
t = 10 # 单位:秒
x = 3e8 # 单位:米
# 相对速度
v = 0.6 * c # 单位:米/秒# 进行洛伦兹正变换
t_prime, x_prime = lorentz_transform(t, x, v)
print(f"正变换后:t' = {t_prime} 秒, x' = {x_prime} 米")# 进行洛伦兹逆变换
t_back, x_back = inverse_lorentz_transform(t_prime, x_prime, v)
print(f"逆变换后:t = {t_back} 秒, x = {x_back} 米")
运行 python test_lorenz.py

相关文章:

python:洛伦兹变换
洛伦兹变换(Lorentz transformations)是相对论中的一个重要概念,特别是在讨论时空的变换时非常重要。在四维时空的背景下,洛伦兹变换描述了在不同惯性参考系之间如何变换时间和空间坐标。在狭义相对论中,洛伦兹变换通常…...

“星门计划对AI未来的意义——以及谁将掌控它”
“星门计划对AI未来的意义——以及谁将掌控它” 图片由DALL-E 3生成 就在几天前,唐纳德特朗普宣布了“星门计划”,OpenAI随即跟进,分享了更多细节。他们明确表示,计划在未来四年内投资5000亿美元,在美国为OpenAI构建一…...

为什么“记住密码”适合持久化?
✅ 特性 1:应用重启后仍需生效 记住密码的本质是长期存储用户的登录凭证(如用户名、密码、JWT Token),即使用户关闭应用、重启设备,仍然可以自动登录。持久化存储方案: React Native 推荐使用 AsyncStorag…...

国产SiC碳化硅功率器件技术成为服务器电源升级的核心引擎
在服务器电源应用中,国产650V碳化硅(SiC)MOSFET逐步取代传统超结(Super Junction, SJ)MOSFET,其核心驱动力源于SiC材料在效率、功率密度、可靠性和长期经济性上的显著优势,叠加产业链成熟与政策…...
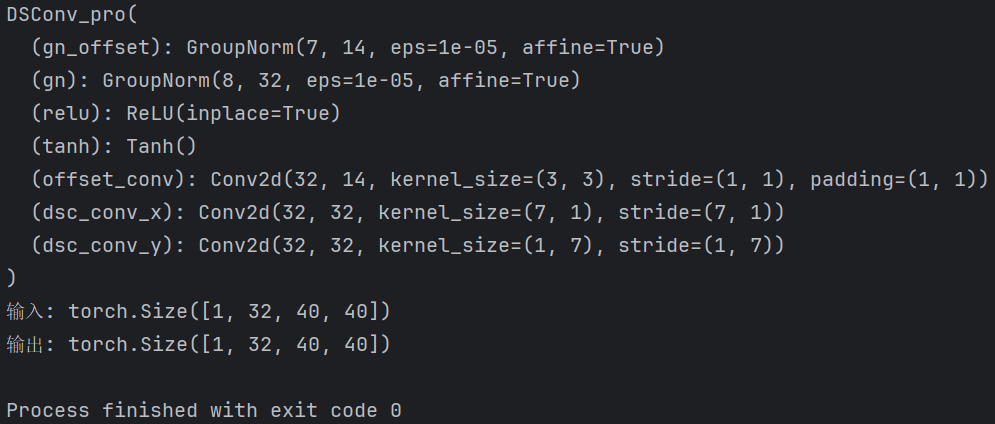
【Block总结】动态蛇形卷积,专注于细长和弯曲的局部结构|即插即用
论文信息 标题: Dynamic Snake Convolution based on Topological Geometric Constraints for Tubular Structure Segmentation 作者: 戚耀磊、何宇霆、戚晓明、张媛、杨冠羽 会议: 2023 IEEE/CVF International Conference on Computer Vision (ICCV) 发表时间: 2023年10月…...

Spring MVC 框架:构建高效 Java Web 应用的利器
Java学习资料 Java学习资料 Java学习资料 一、引言 在 Java Web 开发领域,Spring MVC 框架是一颗耀眼的明星。它作为 Spring 框架家族的重要成员,为开发者提供了一套强大而灵活的解决方案,用于构建 Web 应用程序。Spring MVC 遵循模型 - 视…...
新鲜速递:DeepSeek-R1开源大模型本地部署实战—Ollama + MaxKB 搭建RAG检索增强生成应用
在AI技术快速发展的今天,开源大模型的本地化部署正在成为开发者们的热门实践方向。最火的莫过于吊打OpenAI过亿成本的纯国产DeepSeek开源大模型,就在刚刚,凭一己之力让英伟达大跌18%,纳斯达克大跌3.7%,足足是给中国AI产…...
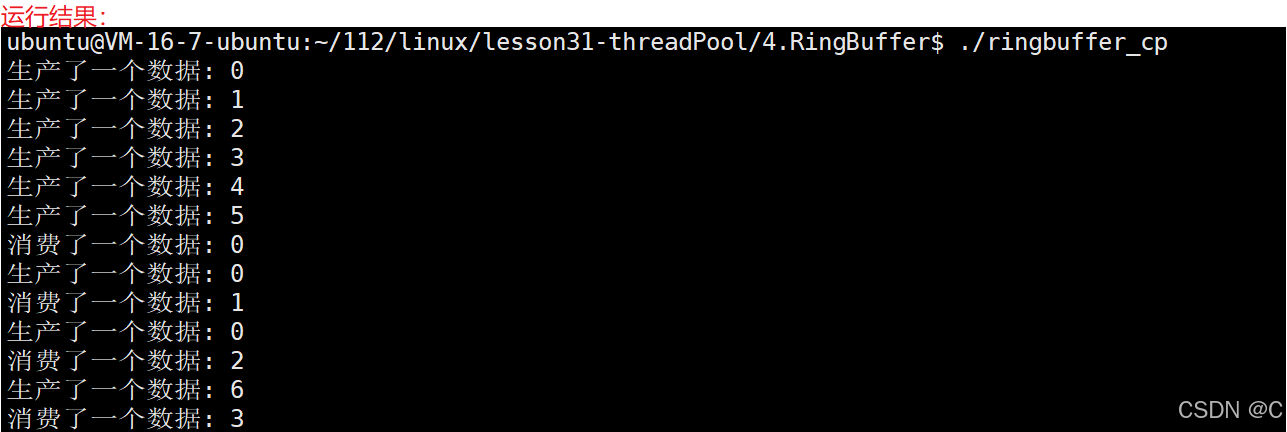
Linux_线程同步生产者消费者模型
同步的相关概念 同步:在保证数据安全的前提下,让线程能够按照某种特定的顺序访问临界资源,从而有效避免饥饿问题,叫做同步竞态条件:因为时序问题,而导致程序异常,我们称之为竞态条件。 同步的…...
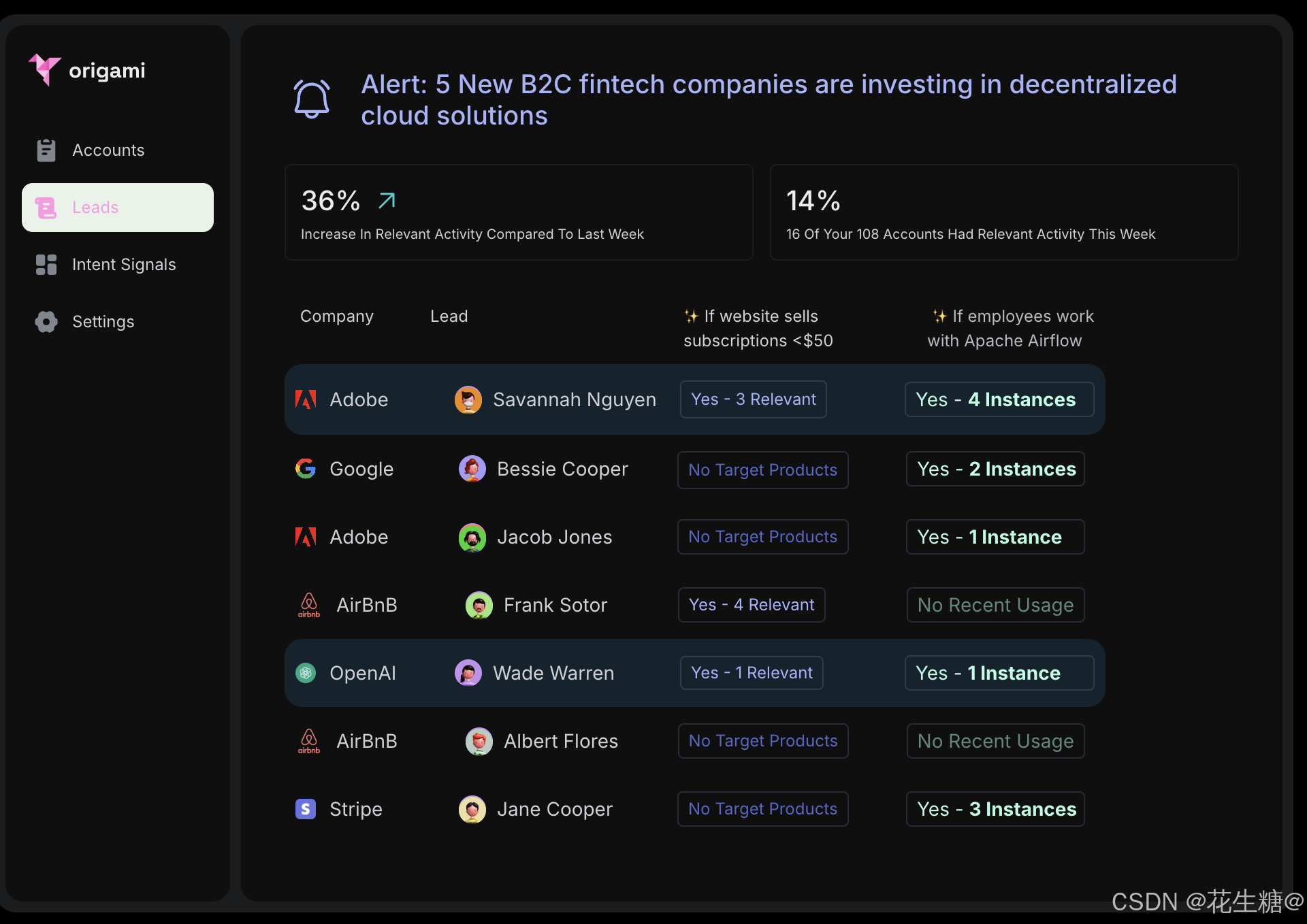
Origami Agents:通过AI驱动的研究工具提升B2B销售效率
在当今竞争激烈的商业环境中,B2B销售团队面临着巨大的挑战,如何高效地发现潜在客户并进行精准的外展活动成为关键。Origami Agents通过其创新的AI驱动研究工具,正在彻底改变这一过程。本文将深入探讨Origami Agents的产品特性、技术架构以及其快速增长背后的成功因素。 一、…...

linux的/proc 和 /sys目录差异
/proc 和 /sys 都是Linux系统中用于提供系统信息和进行系统配置的虚拟文件系统,但它们的原理并不完全一样,以下是具体分析: 目的与功能 /proc :主要用于提供系统进程相关信息以及内核运行时的一些参数等,可让用户和程…...

AIGC时代的Vue或React前端开发
在AIGC(人工智能生成内容)时代,Vue开发正经历着深刻的变革。以下是对AIGC时代Vue开发的详细分析: 一、AIGC技术对Vue开发的影响 代码生成与自动化 AIGC技术使得开发者能够借助智能工具快速生成和优化Vue代码。例如,通…...

代码随想录算法训练营第三十九天-动态规划-337. 打家劫舍 III
老师讲这是树形dp的入门题目解题思路是以二叉树的遍历(递归三部曲)再结合动规五部曲dp数组如何定义:只需要定义一个二个元素的数组,dp[0]与dp[1] dp[0]表示不偷当前节点的最大价值dp[1]表示偷当前节点后的最大价值这样可以把每个节…...
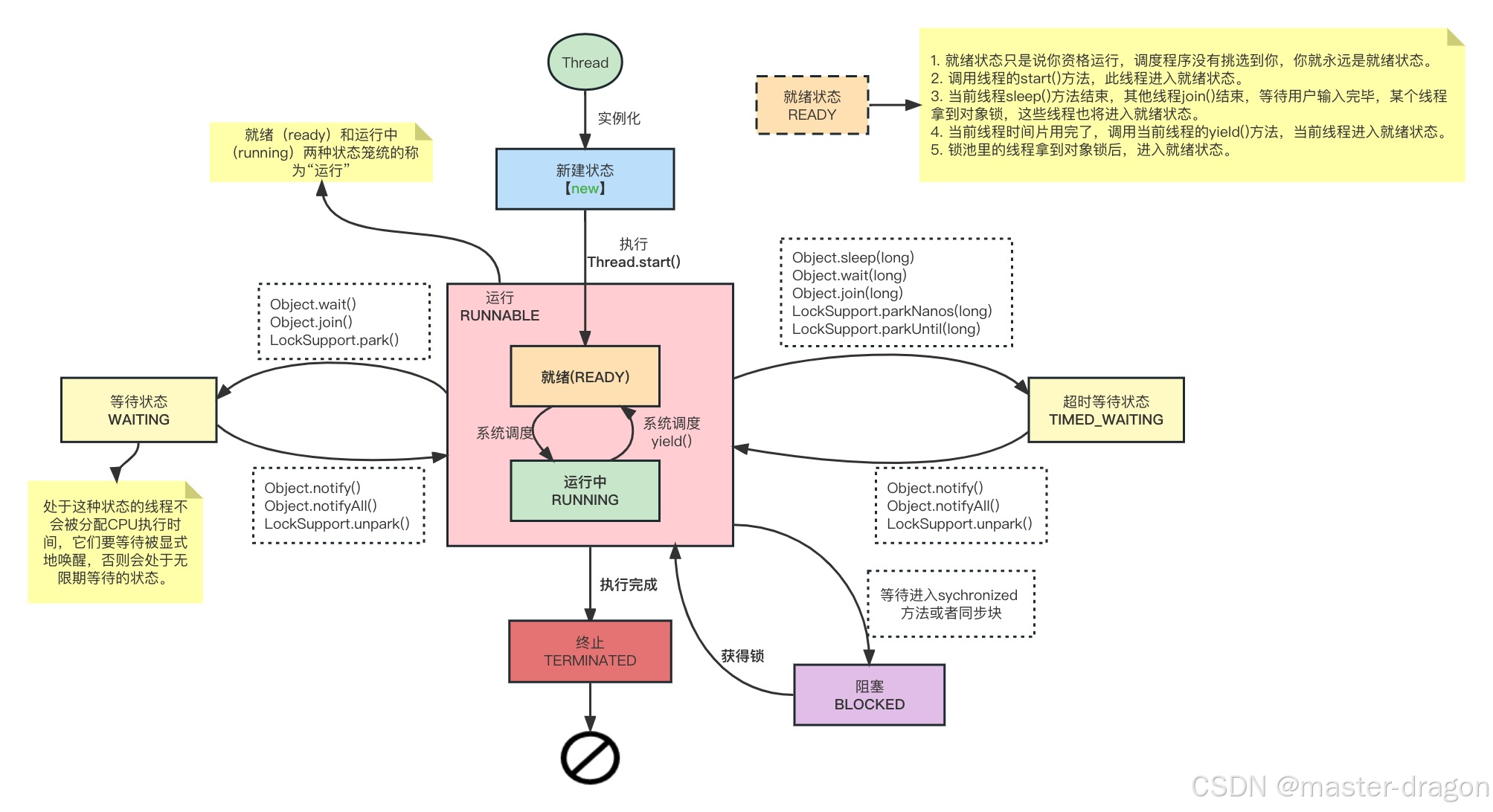
Java线程认识和Object的一些方法
专栏系列文章地址:https://blog.csdn.net/qq_26437925/article/details/145290162 本文目标: 要对Java线程有整体了解,深入认识到里面的一些方法和Object对象方法的区别。认识到Java对象的ObjectMonitor,这有助于后面的Synchron…...
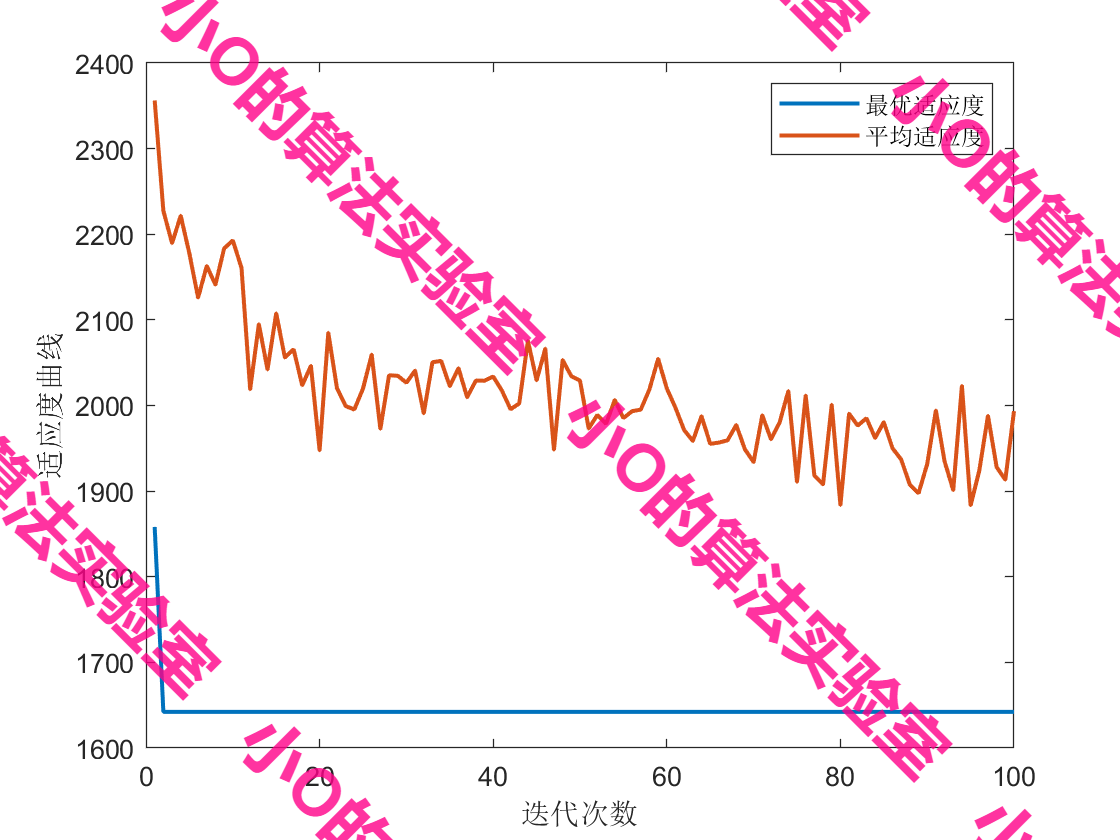
【算法应用】基于A*-蚁群算法求解无人机城市多任务点配送路径问题
目录 1.A星算法原理2.蚁群算法原理3.结果展示4.代码获取 1.A星算法原理 A*算法是一种基于图搜索的智能启发式算法,它具有高稳定性和高节点搜索效率。主要原理为:以起点作为初始节点,将其加入开放列表。从开放列表中选择具有最小总代价值 f (…...

电梯系统的UML文档14
对于 HallButtonControl,我们有二个状态: "门厅灯开 " 和 " 门厅灯关"。 从给出的初始信息,初始的状态应该是"门厅灯关"。行为定义: " 当 HallCall[f,d]是真,则指令 HallLight[f&…...
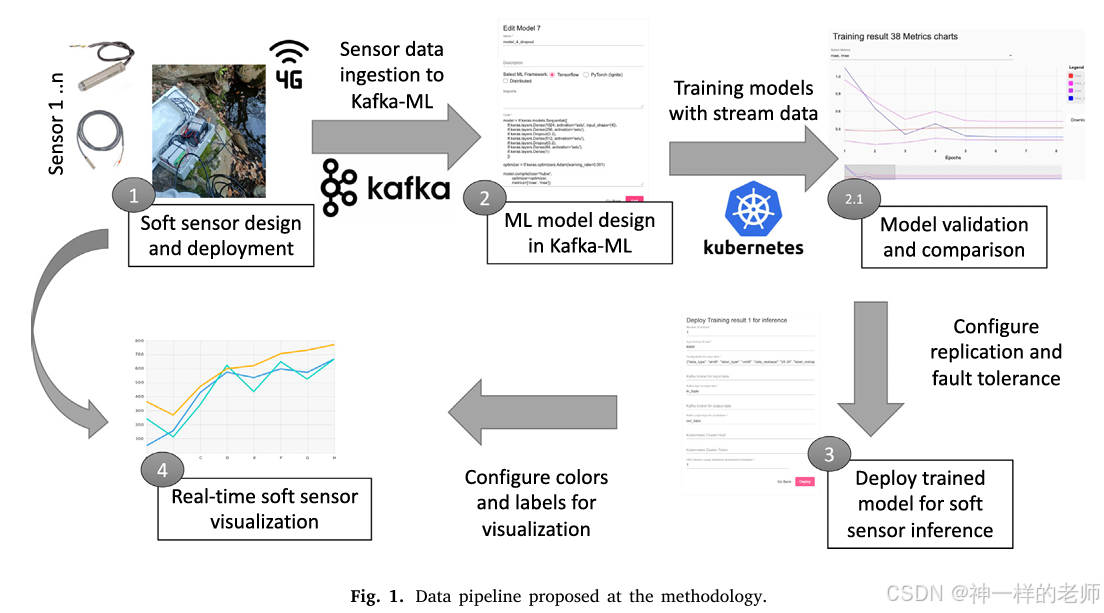
一种用于低成本水质监测的软传感器开源方法:以硝酸盐(NO3⁻)浓度为例
论文标题 A Soft Sensor Open-Source Methodology for Inexpensive Monitoring of Water Quality: A Case Study of NO3− Concentrations 作者信息 Antonio Jess Chaves, ITIS Software, University of Mlaga, 29071 Mlaga, Spain Cristian Martn, ITIS Software, Universi…...

[250130] VirtualBox 7.1.6 维护版本发布 | Anthropic API 推出全新引用功能
目录 VirtualBox 7.1.6 维护版本发布⚙️ 功能改进🛠️ Bug 修复 Anthropic API 推出全新引用功能,让 Claude 的回答更可信 VirtualBox 7.1.6 维护版本发布 VirtualBox 7.1.6 现已发布,这是一个维护版本,主要修复了一些错误并进行…...

JVM_类的加载、链接、初始化、卸载、主动使用、被动使用
①. 说说类加载分几步? ①. 按照Java虚拟机规范,从class文件到加载到内存中的类,到类卸载出内存为止,它的整个生命周期包括如下7个阶段: 第一过程的加载(loading)也称为装载验证、准备、解析3个部分统称为链接(Linking)在Java中数据类型分为基本数据类型和引用数据…...

2025最新版MySQL安装使用指南
2025最新版MySQL安装使用指南 The Installation and Usage Guide of the Latest Version of Oracle MySQL in 2025 By JacksonML 1. 获取MySQL 打开Chrome浏览器,访问官网链接:https://www.mysql.com/ ,随即打开MySQL官网主页面ÿ…...

MIMIC IV数据库中mimiciv_hosp的transfers表的careunit分析
以下是MIMIC IV数据库中mimiciv_hosp的transfers表的careunit的所有值,从医学专业角度分析,下面哪些科室会有实施心脏或神经手术? Cardiac Surgery Cardiac Vascular Intensive Care Unit (CVICU) Cardiology Cardiology Surgery Intermediat…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

