Signature
Signature
题目是:
import ecdsaimport randomdef ecdsa_test(dA,k):sk = ecdsa.SigningKey.from_secret_exponent(secexp=dA,curve=ecdsa.SECP256k1)sig1 = sk.sign(data=b'Hi.', k=k).hex()sig2 = sk.sign(data=b'hello.', k=k).hex()#不同的kr1 = int(sig1[:64], 16)s1 = int(sig1[64:], 16)s2 = int(sig2[64:], 16)return r1,s1,s2if __name__ == '__main__':n = 0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141a = random.randint(0,n)flag = 'flag{' + str(a) + "}"b = random.randint(0,n)print(ecdsa_test(a,b))# (4690192503304946823926998585663150874421527890534303129755098666293734606680, 111157363347893999914897601390136910031659525525419989250638426589503279490788, 74486305819584508240056247318325239805160339288252987178597122489325719901254)分析代码可以看出,存在随机数重复使用。
具体来说,这段代码中签名的过程中使用了相同的随机数 k 来对不同的消息进行签名。
这种情况下,可以通过分析两个相同 k 值对应的消息签名来恢复私钥 dA。
import sympyfrom hashlib import sha1from Cryptodome.Util.number import long_to_bytes , bytes_to_longdef calculate_private_key(r1, s1, s2, h1, h2, n):# 计算k值k = ((h1 - h2) * sympy.mod_inverse(s1 - s2, n)) % n# 计算私钥dAdA = (sympy.mod_inverse(r1, n) * (k * s1 - h1)) % nreturn dAif __name__ == "__main__":# 定义椭圆曲线的参数n = 0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141# 签名中的r1, s1, s2值r1 = 4690192503304946823926998585663150874421527890534303129755098666293734606680s1 = 111157363347893999914897601390136910031659525525419989250638426589503279490788s2 = 74486305819584508240056247318325239805160339288252987178597122489325719901254h1 = bytes_to_long(sha1(b'Hi.').digest())h2 = bytes_to_long(sha1(b'hello.').digest())private_key = calculate_private_key(r1, s1, s2, h1, h2, n)print(f'flag{{{private_key}}}')---------------------------------------------------------flag{40355055231406097504270940121798355439363616832290875140843417522164091270174} 椭圆曲线数字签名算法(Elliptic Curve Digital Signature Algorithm,ECDSA)是一种基于椭圆曲线密码学的数字签名算法。它广泛应用于需要确保数据完整性和身份验证的场景中,例如在区块链技术(如比特币)、安全通信协议(如TLS/SSL)等领域。
-
基本原理
ECDSA 是一种非对称加密算法,它基于椭圆曲线数学的复杂性来实现数字签名的生成和验证。其核心思想是利用椭圆曲线上的点的加法运算和标量乘法运算,这些运算在数学上是单向的,即很容易进行正向计算,但很难进行逆向求解。
-
椭圆曲线:椭圆曲线是一种特殊的数学曲线。椭圆曲线上的点具有特殊的代数结构,使得点的加法和标量乘法运算可以高效地实现。
-
私钥和公钥:在 ECDSA 中,私钥是一个随机生成的大整数 d,公钥是椭圆曲线上的一个点 Q,通过 Q=d×G 计算得到,其中 G是椭圆曲线上的一个基点。
-
签名生成过程
签名生成过程主要包括以下步骤:
-
选择随机数:签名者选择一个随机整数 k(称为临时私钥),并计算椭圆曲线上的点 R=k×G。
-
计算 r 和 s:
-
r 是点 R 的 x 坐标对模数 n(椭圆曲线的阶)取模的结果。
-
s=k−1(H(m)+d⋅r)mod n,其中 H(m) 是消息 m 的哈希值,k−1 是 k 的模逆元。
-
-
输出签名:签名由 (r,s) 组成。
-
签名验证过程
验证签名的过程主要包括以下步骤:
-
计算 w:验证者计算 w=s−1mod n。
-
计算 u1 和 u2:
-
u1=H(m)⋅w mod n
-
u2=r⋅w mod n
-
-
计算点 R′:计算 R′=u1×G+u2×Q。
-
验证 r:检查 r 是否等于 R′ 的 x 坐标对模数 n 取模的结果。如果相等,则签名验证通过,否则验证失败。
相关文章:

Signature
Signature 题目是: import ecdsaimport randomdef ecdsa_test(dA,k):sk ecdsa.SigningKey.from_secret_exponent(secexpdA,curveecdsa.SECP256k1)sig1 sk.sign(databHi., kk).hex()sig2 sk.sign(databhello., kk).hex()#不同的kr1 int(sig1[:64], 16)s1 i…...

93,【1】buuctf web [网鼎杯 2020 朱雀组]phpweb
进入靶场 页面一直在刷新 在 PHP 中,date() 函数是一个非常常用的处理日期和时间的函数,所以应该用到了 再看看警告的那句话 Warning: date(): It is not safe to rely on the systems timezone settings. You are *required* to use the date.timez…...
笔灵ai写作技术浅析(四):知识图谱
知识图谱(Knowledge Graph)是一种结构化的知识表示方式,通过将知识以图的形式进行组织,帮助AI系统更好地理解和利用信息。在笔灵AI写作中,知识图谱技术被广泛应用于结构化组织各种领域的知识,使AI能够根据写作主题快速获取相关的背景知识、概念关系等,从而为生成内容提供…...
Chromium132 编译指南 - Android 篇(四):配置 depot_tools
1. 引言 在前面的章节中,我们详细介绍了编译 Chromium 132 for Android 所需的系统和硬件要求,以及如何安装和配置基础开发环境和常用工具。完成这些步骤后,接下来需要配置 depot_tools,这是编译 Chromium 的关键工具集。depot_t…...

使用真实 Elasticsearch 进行高级集成测试
作者:来自 Elastic Piotr Przybyl 掌握高级 Elasticsearch 集成测试:更快、更智能、更优化。 在上一篇关于集成测试的文章中,我们介绍了如何通过改变数据初始化策略来缩短依赖于真实 Elasticsearch 的集成测试的执行时间。在本期中࿰…...

SQL进阶实战技巧:如何分析浏览到下单各步骤转化率及流失用户数?
目录 0 问题描述 1 数据准备 2 问题分析 3 问题拓展 3.1 跳出率计算...
机器学习--概览
一、机器学习基础概念 1. 定义 机器学习(Machine Learning, ML):通过算法让计算机从数据中自动学习规律,并利用学习到的模型进行预测或决策,而无需显式编程。 2. 与编程的区别 传统编程机器学习输入:规…...

低代码系统-产品架构案例介绍、炎黄盈动-易鲸云(十二)
易鲸云作为炎黄盈动新推出的产品,在定位上为低零代码产品。 开发层 表单引擎 表单设计器,包括设计和渲染 流程引擎 流程设计,包括设计和渲染,需要说明的是:采用国际标准BPMN2.0,可以全球通用 视图引擎 视图…...
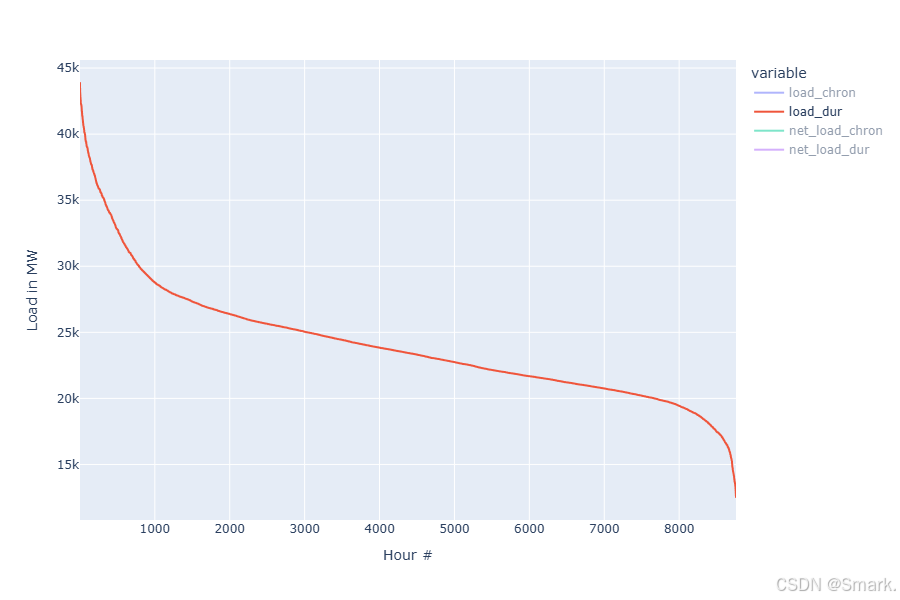
Electricity Market Optimization 探索系列(二)
本文参考链接link 负荷持续时间曲线 (Load Duration Curve),是根据实际的符合数据进行降序排序之后得到的一个曲线 这个曲线能够发现负荷在某个区间时,将会持续多长时间,有助于发电容量的规划 净负荷(net load) 是指预期负荷和预期可再生…...

OpenAI 实战进阶教程 - 第一节:OpenAI API 架构与基础调用
目标 掌握 OpenAI API 的基础调用方法。理解如何通过 API 进行内容生成。使用实际应用场景帮助零基础读者理解 API 的基本用法。 一、什么是 OpenAI API? OpenAI API 是一种工具,允许开发者通过编程方式与 OpenAI 的强大语言模型(例如 gpt-…...
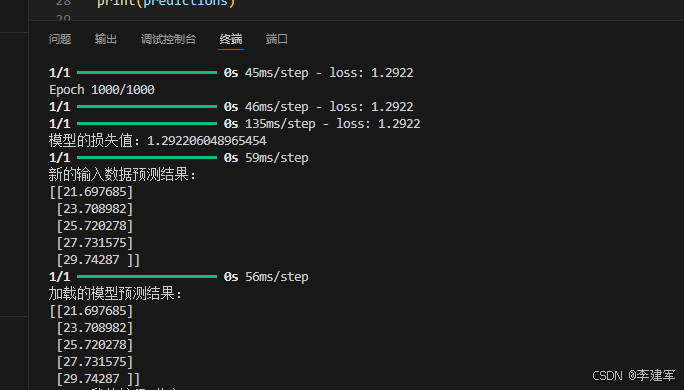
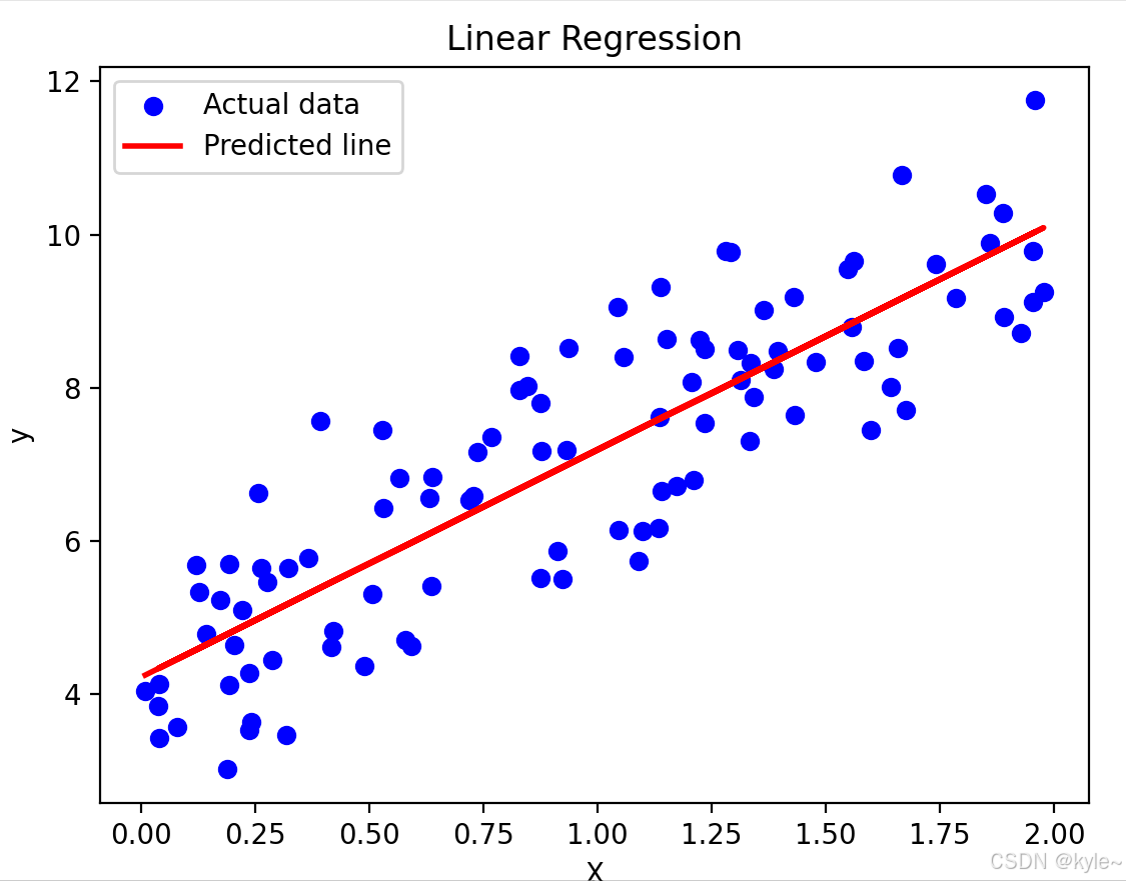
TensorFlow简单的线性回归任务
如何使用 TensorFlow 和 Keras 创建、训练并进行预测 1. 数据准备与预处理 2. 构建模型 3. 编译模型 4. 训练模型 5. 评估模型 6. 模型应用与预测 7. 保存与加载模型 8.完整代码 1. 数据准备与预处理 我们将使用一个简单的线性回归问题,其中输入特征 x 和标…...

【视频+图文详解】HTML基础4-html标签的基本使用
图文教程 html标签的基本使用 无序列表 作用:定义一个没有顺序的列表结构 由两个标签组成:<ul>以及<li>(两个标签都属于容器级标签,其中ul只能嵌套li标签,但li标签能嵌套任何标签,甚至ul标…...

在Arm芯片苹果Mac系统上通过homebrew安装多版本mysql并解决各种报错,感谢deepseek帮助解决部分问题
背景: 1.苹果设备上安装mysql,随着苹果芯片的推出,很多地方都变得不一样了。 2.很多时候为了老项目能运行,我们需要能安装mysql5.7或者mysql8.0或者mysql8.2.虽然本文编写时最新的默认mysql已经是9.2版本。 安装步骤 1.执行hom…...

c++可变参数详解
目录 引言 库的基本功能 va_start 宏: va_arg 宏 va_end 宏 va_copy 宏 使用 处理可变参数代码 C11可变参数模板 基本概念 sizeof... 运算符 包扩展 引言 在C编程中,处理不确定数量的参数是一个常见的需求。为了支持这种需求,C标准库提供了 &…...
【深度分析】DeepSeek 遭暴力破解,攻击 IP 均来自美国,造成影响有多大?有哪些好的防御措施?
技术铁幕下的暗战:当算力博弈演变为代码战争 一场针对中国AI独角兽的全球首例国家级密码爆破,揭开了数字时代技术博弈的残酷真相。DeepSeek服务器日志中持续跳动的美国IP地址,不仅是网络攻击的地理坐标,更是技术霸权对新兴挑战者的…...
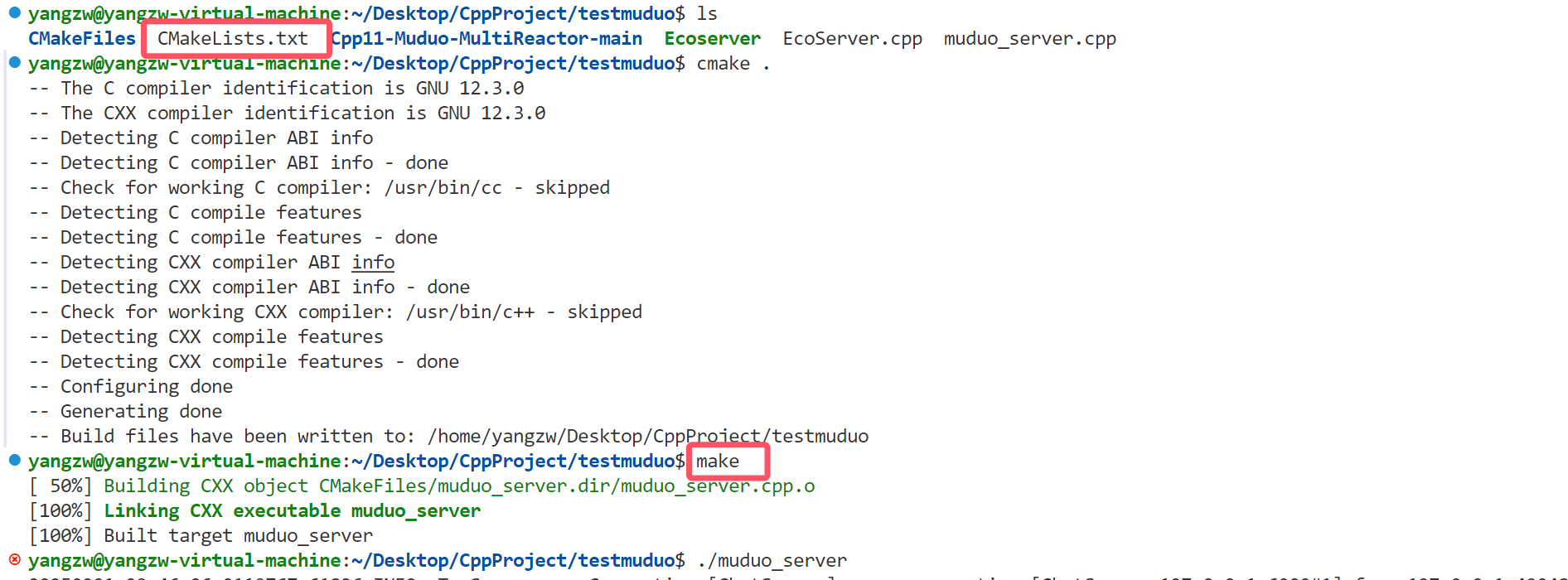
CMake项目编译与开源项目目录结构
Cmake 使用简单方便,可以跨平台构建项目编译环境,尤其比直接写makefile简单,可以通过简单的Cmake生成负责的Makefile文件。 如果没有使用cmake进行编译,需要如下命令:(以muduo库echo服务器为例)…...

完全卸载mysql server步骤
1. 在控制面板中卸载mysql 2. 打开注册表,运行regedit, 删除mysql信息 HKEY_LOCAL_MACHINE-> SYSTEM->CurrentContolSet->Services->EventLog->Application->Mysql HKEY_LOCAL_MACHINE-> SYSTEM->CurrentContolSet->Services->Mysql …...
)
C#方法(练习)
1.定义一个函数,输入三个值,找出三个数中的最小值 2.定义一个函数,输入三个值,找出三个数中的最大值 3.定义一个函数,输入三个值,找出三个数中的平均值 4.定义一个函数,计算一个数的 N 次方 Pow(2, 3)返回8 5.传入十一…...
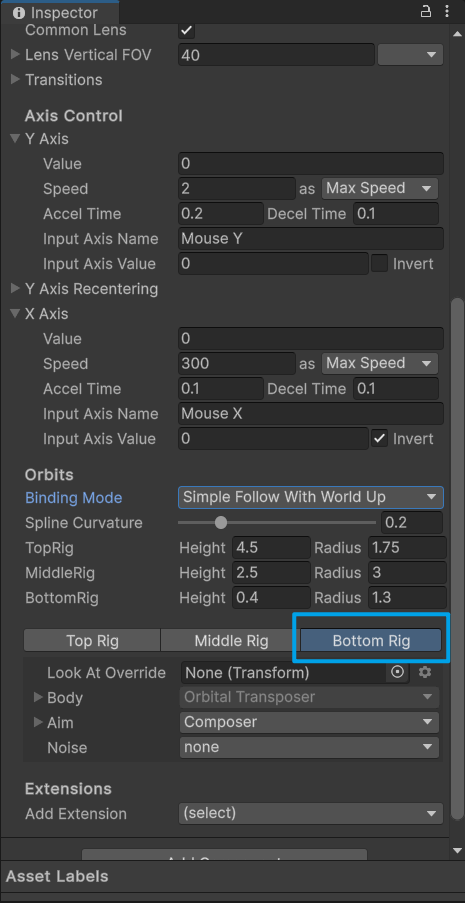
Unity游戏(Assault空对地打击)开发(3) 摄像机的控制
详细步骤 打开My Assets或者Package Manager。 选择Unity Registry。 搜索Cinemachine,找到 Cinemachine包,点击 Install按钮进行安装。 关闭窗口,新建一个FreeLook Camera,如下。 接着新建一个对象Pos,拖到Player下面…...

ChatGPT-4o和ChatGPT-4o mini的差异点
在人工智能领域,OpenAI再次引领创新潮流,近日正式发布了其最新模型——ChatGPT-4o及其经济实惠的小型版本ChatGPT-4o Mini。这两款模型虽同属于ChatGPT系列,但在性能、应用场景及成本上展现出显著的差异。本文将通过图文并茂的方式࿰…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...
