python算法和数据结构刷题[5]:动态规划
动态规划(Dynamic Programming, DP)是一种算法思想,用于解决具有最优子结构的问题。它通过将大问题分解为小问题,并找到这些小问题的最优解,从而得到整个问题的最优解。动态规划与分治法相似,但区别在于动态规划的子问题通常不是相互独立的。
动态规划的核心是解决重复子问题。例如,斐波那
契数列问题,可以通过递归实现,但效率低下,因为会有重复计算。动态规划通过存储已解决的子问题的答案,避免重复计算,从而提高效率。这种方法需要额外的存储空间,是一种空间换时间的策略。
如果一个问题,可以把所有可能的答案穷举出来,并且穷举出来后,发现存在重叠子问题,就可以考虑使用动态规划。
单维动态规划
斐波那契数列
def fibonacci(n):# 如果n小于等于1,直接返回nif n <= 1:return n# 初始化dp数组,用于存储从0到n的斐波那契数dp = [0] * (n + 1)dp[1] = 1 # 斐波那契数列的第二个数是1# 使用动态规划填充dp数组for i in range(2, n + 1):dp[i] = dp[i - 1] + dp[i - 2]# 返回第n个斐波那契数return dp[n]# 测试代码
print(fibonacci(0)) # 输出 0
print(fibonacci(1)) # 输出 1
print(fibonacci(2)) # 输出 1
print(fibonacci(3)) # 输出 2
print(fibonacci(4)) # 输出 3
print(fibonacci(5)) # 输出 5
print(fibonacci(6)) # 输出 8
print(fibonacci(7)) # 输出 1370. 爬楼梯 - 力扣(LeetCode)
到达第 n 个台阶的方法数等于到达第 n-1 个台阶和第 n-2 个台阶的方法数之和
class Solution:def climbStairs(self, n: int) -> int:f = [0] * (n + 1)f[0] = f[1] = 1for i in range(2, n + 1):f[i] = f[i - 1] + f[i - 2]return f[n]118. 杨辉三角 - 力扣(LeetCode)

给出一个整数输出杨辉三角

class Solution:def generate(self, numRows: int) -> List[List[int]]:dp = [[0] * i for i in range(1, numRows + 1)]for i in range(numRows):dp[i][0] = 1dp[i][i] = 1res = []for i in range(numRows):for j in range(i):if i != 0 and j != 0:dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]res.append(dp[i])return res322. 零钱兑换 - 力扣(LeetCode)
背包问题:背包问题通常描述为:给定一组物品,每个物品有一定的价值(value)和重量(weight),需要从中选择一些物品放入一个给定容量的背包中,使得放入背包的物品的总价值最大,同时不超过背包的容量。
完全背包问题
返回构成该金额所需的最少硬币数量。如果该金额无法通过硬币的任何组合来弥补,则返回 。-1
def coinChange(coins, amount):# 创建一个数组,长度为 amount + 1,初始值为 amount + 1dp = [amount + 1] * (amount + 1)# 金额为0时,需要0个硬币dp[0] = 0# 遍历每个金额for a in range(1, amount + 1):# 遍历每种硬币for coin in coins:# 如果当前硬币面额小于等于当前金额if coin <= a:# 更新 dp[a] 为使用当前硬币后的最少硬币数量dp[a] = min(dp[a], dp[a - coin] + 1)# 如果 dp[amount] 还是初始值,则返回 -1,否则返回 dp[amount]return dp[amount] if dp[amount] != amount + 1 else -1# 示例
coins = [1, 2, 5]
amount = 11
print(coinChange(coins, amount)) # 输出应该是 3279. 完全平方数 - 力扣(LeetCode)
完全背包问题
def numSquares(n):# 创建一个数组来存储每个数字的最小完全平方数个数,初始值为0dp = [0] * (n + 1)#,用于存储每个数字 i 可以表示为完全平方数之和的最小数量。 # 初始化dp数组,每个位置初始为最大值for i in range(1, n + 1):dp[i] = i # 最坏的情况是 i 个 1 的平方# 遍历每个数字,更新其最小完全平方数个数for i in range(1, n + 1):j = 1while j * j <= i:dp[i] = min(dp[i], dp[i - j * j] + 1)j += 1# 返回n的最小完全平方数个数return dp[n]# 示例
print(numSquares(12)) # 输出应为 3
print(numSquares(13)) # 输出应为 2,因为 13 = 4 + 9198. 打家劫舍 - 力扣(LeetCode)

def rob(nums):if not nums:return 0if len(nums) == 1:return nums[0]dp = [0] * len(nums)dp[0] = nums[0]dp[1] = max(nums[0], nums[1])for i in range(2, len(nums)):dp[i] = max(dp[i-1], dp[i-2] + nums[i])return dp[-1]# 示例
nums = [2, 7, 9, 3, 1]
print(rob(nums)) # 输出应该是 12,因为抢第 0、2、4 间房子(2+9+1)139. 单词拆分 - 力扣(LeetCode)

def wordBreak(s, wordDict):# 首先创建一个布尔数组 dp,长度为字符串长度加一,初始化所有值为 Falsedp = [False] * (len(s) + 1)# dp[i] 将表示 s 的前 i 个字符是否可以被成功分割dp[0] = True # 空字符串可以被成功分割# 遍历字符串的每一个字符for i in range(1, len(s) + 1):# 对于每一个可能的结束位置 i,检查所有可能的开始位置 jfor j in range(i):# 如果 dp[j] 为 True,且 s[j:i] 在字典中,那么 dp[i] 也为 Trueif dp[j] and s[j:i] in wordDict:dp[i] = Truebreak # 找到一个有效的分割就跳出内层循环# 返回 dp[len(s)],它表示整个字符串是否可以被成功分割return dp[len(s)]# 示例用法
swordDict = ["apple", "pen", "applepen", "pine", "pineapple"]
s = "pineapplepenapple"
print(wordBreak(s, swordDict)) # 应该返回 True300. 最长递增子序列 - 力扣(LeetCode)
最长递增子序列:可以不连续但是前后相对顺序不变
def lengthOfLIS(nums):if not nums:return 0# 初始化一个数组 dp,长度与输入数组相同,所有元素初始为 1# dp[i] 表示以 nums[i] 结尾的最长递增子序列的长度dp = [1] * len(nums)# 遍历数组,计算每个位置的最长递增子序列长度for i in range(1, len(nums)):for j in range(i):# 如果当前元素 nums[i] 大于之前的元素 nums[j]# 并且以 nums[i] 结尾的子序列长度可以增加if nums[i] > nums[j]:dp[i] = max(dp[i], dp[j] + 1)# 返回 dp 数组中的最大值,即为最长递增子序列的长度return max(dp)# 示例用法
nums = [10, 9, 2, 5, 3, 7, 101, 18]
print(lengthOfLIS(nums)) # 输出应该是 4,因为最长递增子序列是 [2, 3, 7, 101]重点:如果 nums[i] 大于 nums[j],那么我们可以将 nums[i] 添加到以 nums[j] 结尾的递增子序列中,从而形成一个更长的递增子序列。
152. 乘积最大子数组 - 力扣(LeetCode)
最大乘积子数组问题是指在一个整数数组中找到一个连续的子数组(至少包含一个数),使得这个子数组中所有数的乘积是最大的。
tmp = imax;
imax = imin;
imin = tmp;def maxProduct(nums):# 初始化最大乘积、当前最大乘积和当前最小乘积max_so_far = nums[0]min_so_far = nums[0]result = nums[0]# 遍历数组,从第二个元素开始for i in range(1, len(nums)):# 如果当前元素是负数,那么最大乘积和最小乘积会交换if nums[i] < 0:max_so_far, min_so_far = min_so_far, max_so_far# 更新当前最大乘积和最小乘积max_so_far = max(nums[i], max_so_far * nums[i])min_so_far = min(nums[i], min_so_far * nums[i])# 更新结果为最大乘积result = max(result, max_so_far)return result# 示例
nums = [2, 3, -2, 4]
print(maxProduct(nums)) # 输出: 6416. 分割等和子集 - 力扣(LeetCode)
给定一个整数数组 ,如果您可以将数组划分为两个子集,使得两个子集中的元素之和相等,则 返回。
01背包问题
def canPartition(nums):total_sum = sum(nums)# 如果总和是奇数,直接返回 Falseif total_sum % 2 != 0:return Falsetarget = total_sum // 2dp = [False] * (target + 1)dp[0] = True # 0 总是可以达成,不选择任何元素即可# 遍历所有物品(数组中的数字)for num in nums:# 这里必须从 target 递减到 num,以防止一个物品被重复使用for j in range(target, num - 1, -1):# 如果 dp[j - num] 是 True,则 dp[j] 也应该是 Truedp[j] = dp[j] or dp[j - num]# dp[target] 表示是否可以从数组中选取一些数字,使得这些数字的总和等于 targetreturn dp[target]# 示例
nums = [1, 5, 11, 5]
print(canPartition(nums)) # 输出: True32. 最长有效括号 - 力扣(LeetCode)
当前字符是 ) 并且前一个字符是 (,当前字符是 ) 并且前一个字符也是 ):s = "()(())"
def longest_valid_parentheses(s):n = len(s)if n == 0:return 0# dp[i] 表示以 s[i] 结尾的最长有效括号的长度dp = [0] * nmax_len = 0for i in range(1, n):if s[i] == ')':# 如果前一个字符是'(',则可以形成一个有效的括号对if s[i - 1] == '(':dp[i] = (dp[i - 2] if i >= 2 else 0) + 2# 如果前一个字符是')',并且前面的有效括号长度为 dp[i - 1]# 并且 dp[i - 1] 前面的字符是'(',则可以扩展有效括号长度elif i - dp[i - 1] > 0 and s[i - dp[i - 1] - 1] == '(':dp[i] = dp[i - 1] + (dp[i - dp[i - 1] - 2] if i - dp[i - 1] >= 2 else 0) + 2max_len = max(max_len, dp[i])return max_len# 示例
print(longest_valid_parentheses("(()")) # 输出 2
print(longest_valid_parentheses(")()())")) # 输出 4多维动态规划
62. 不同路径 - 力扣(LeetCode)
与杨辉三角和爬楼梯类似
空间复杂度:2n
class Solution:def uniquePaths(self, m: int, n: int) -> int:pre = [1] * ncur = [1] * nfor i in range(1, m):for j in range(1, n):cur[j] = pre[j] + cur[j-1]pre = cur[:]return pre[-1]64. 最小路径和 - 力扣(LeetCode)
向下或向右移动从左上角到右下角的最小路径和
到达每个单元格 (i, j) 的最小路径和可以由到达其上方单元格 (i-1, j) 和左方单元格 (i, j-1) 的最小路径和推导出来。
dp[i][j] 表示到达单元格 (i, j) 的最小路径和,到达 (i, j) 的最小路径和等于到达其上方和左方单元格的最小路径和中的较小者,再加上当前单元格的值。
def min_path_sum(grid):if not grid or not grid[0]:return 0m, n = len(grid), len(grid[0])dp = [[0] * n for _ in range(m)]# 初始化左上角dp[0][0] = grid[0][0]# 初始化第一列for i in range(1, m):dp[i][0] = dp[i - 1][0] + grid[i][0]# 初始化第一行for j in range(1, n):dp[0][j] = dp[0][j - 1] + grid[0][j]# 填充dp数组剩余部分for i in range(1, m):for j in range(1, n):# dp[i][j]可以从上方(dp[i-1][j])或左方(dp[i][j-1])到达,# 所以我们取两者的最小值,并加上当前格子的值。dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j]# 右下角的格子将包含从左上角到右下角的最小路径和return dp[m - 1][n - 1]5. 最长回文子串 - 力扣(LeetCode)
记录字符串中每对字符之间是否形成回文子串
def longest_palindromic_substring(s):n = len(s)if n == 0:return ""# 初始化一个二维数组,用于存储子串是否为回文dp = [[False] * n for _ in range(n)]start = 0 # 最长回文子串的起始位置max_length = 1 # 最长回文子串的长度# 所有长度为1的子串都是回文for i in range(n):dp[i][i] = True# 检查长度为2的子串是否为回文for i in range(n - 1):if s[i] == s[i + 1]:dp[i][i + 1] = Truestart = imax_length = 2# 检查长度大于2的子串for length in range(3, n + 1): # 子串长度从3开始递增for i in range(n - length + 1):j = i + length - 1 # 子串的结束位置# 检查子串s[i:j+1]是否为回文if s[i] == s[j] and dp[i + 1][j - 1]:dp[i][j] = Truestart = imax_length = length# 返回最长回文子串return s[start:start + max_length]# 示例使用
s = "babad"
print(longest_palindromic_substring(s)) # 输出可能是"bab"或"aba"1143. 最长公共子序列 - 力扣(LeetCode)
子序列可以是不连续的;子数组(子字符串)需要是连续的。
def longest_common_subsequence(text1, text2):# 获取两个字符串的长度m, n = len(text1), len(text2)# 初始化一个二维数组 dp,用于存储子问题的解# dp[i][j] 表示 text1 的前 i 个字符和 text2 的前 j 个字符的最长公共子序列的长度dp = [[0] * (n + 1) for _ in range(m + 1)]# 填充 dp 数组for i in range(1, m + 1):for j in range(1, n + 1):# 如果当前字符相同,则最长公共子序列长度加一if text1[i - 1] == text2[j - 1]:dp[i][j] = dp[i - 1][j - 1] + 1else:# 如果当前字符不同,取左上角、上方、左方三个方向的最大值dp[i][j] = max(dp[i - 1][j], dp[i][j - 1], dp[i - 1][j - 1])# dp[m][n] 即为两个字符串的最长公共子序列的长度return dp[m][n]# 测试用例
text1 = "abcde"
text2 = "ace"
# 测试结果
print(longest_common_subsequence(text1, text2)) 72. 编辑距离 - 力扣(LeetCode)
定两个字符串 和 ,返回将 word1 转换为 word2 所需的最小步数
def minDistance(word1, word2):# 创建一个矩阵来存储子问题的解dp = [[0 for x in range(len(word2) + 1)] for x in range(len(word1) + 1)]# 初始化矩阵的第一行和第一列for i in range(len(word1) + 1):dp[i][0] = ifor j in range(len(word2) + 1):dp[0][j] = j# 填充dp矩阵for i in range(1, len(word1) + 1):for j in range(1, len(word2) + 1):# 如果当前字符相同,无需编辑,直接使用上一个状态的值if word1[i - 1] == word2[j - 1]:dp[i][j] = dp[i - 1][j - 1]else:# 如果字符不同,取插入、删除、替换三者的最小值加1dp[i][j] = 1 + min(dp[i - 1][j], # 删除dp[i][j - 1], # 插入dp[i - 1][j - 1] # 替换)# dp矩阵的最后一个元素即为编辑距离return dp[len(word1)][len(word2)]# 示例使用
word1 = "horse"
word2 = "ros"
print(minDistance(word1, word2)) # 输出应该是3,因为"horse" -> "ros"需要3步:h -> r, o ->相关文章:

python算法和数据结构刷题[5]:动态规划
动态规划(Dynamic Programming, DP)是一种算法思想,用于解决具有最优子结构的问题。它通过将大问题分解为小问题,并找到这些小问题的最优解,从而得到整个问题的最优解。动态规划与分治法相似,但区别在于动态…...

Ollama+OpenWebUI部署本地大模型
OllamaOpenWebUI部署本地大模型 前言 Ollama是一个强大且易于使用的本地大模型推理框架,它专注于简化和优化大型语言模型(LLMs)在本地环境中的部署、管理和推理工作流。可以将Ollama理解为一个大模型推理框架的后端服务。 Ollama Ollama安…...
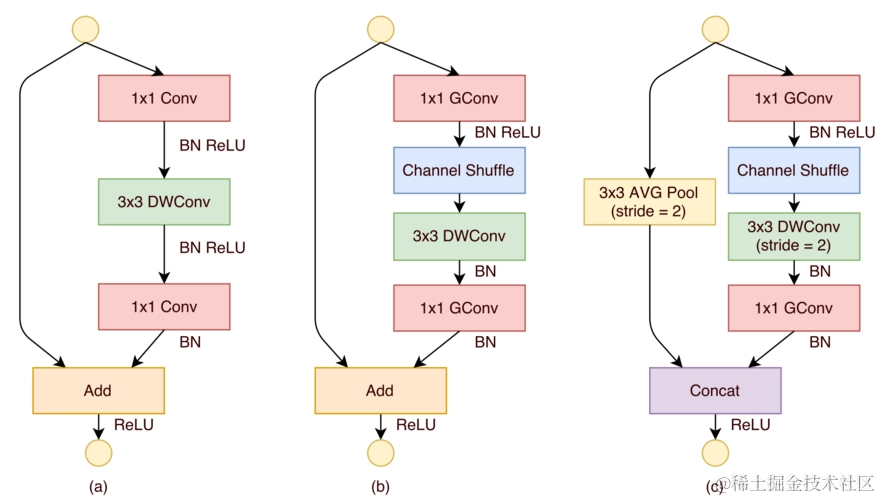
Python从0到100(八十六):神经网络-ShuffleNet通道混合轻量级网络的深入介绍
前言: 零基础学Python:Python从0到100最新最全教程。 想做这件事情很久了,这次我更新了自己所写过的所有博客,汇集成了Python从0到100,共一百节课,帮助大家一个月时间里从零基础到学习Python基础语法、Pyth…...

【网络】传输层协议TCP(重点)
文章目录 1. TCP协议段格式2. 详解TCP2.1 4位首部长度2.2 32位序号与32位确认序号(确认应答机制)2.3 超时重传机制2.4 连接管理机制(3次握手、4次挥手 3个标志位)2.5 16位窗口大小(流量控制)2.6 滑动窗口2.7 3个标志位 16位紧急…...

海思ISP开发说明
1、概述 ISP(Image Signal Processor)图像信号处理器是专门用于处理图像信号的硬件或处理单元,广泛应用于图像传感器(如 CMOS 或 CCD 传感器)与显示设备之间的信号转换过程中。ISP通过一系列数字图像处理算法完成对数字…...

实验十 Servlet(一)
实验十 Servlet(一) 【实验目的】 1.了解Servlet运行原理 2.掌握Servlet实现方式 【实验内容】 1、参考课堂例子,客户端通过login.jsp发出登录请求,请求提交到loginServlet处理。如果用户名和密码相同则视为登录成功,…...

doris:聚合模型的导入更新
这篇文档主要介绍 Doris 聚合模型上基于导入的更新。 整行更新 使用 Doris 支持的 Stream Load,Broker Load,Routine Load,Insert Into 等导入方式,往聚合模型(Agg 模型)中进行数据导入时,都…...

Java NIO_非阻塞I/O的实现与优化
1. 引言 1.1 背景介绍 随着互联网应用的快速发展,传统的阻塞I/O模型已经无法满足高并发、高性能的需求。Java NIO(Non-blocking I/O)提供了高效的非阻塞I/O操作,使得开发者能够构建高性能的网络应用和文件处理系统。 1.2 Java NIO的重要性 Java NIO通过非阻塞I/O和多路…...

代码随想录算法训练营Day51 | 101.孤岛的总面积、102.沉没孤岛、103.水流问题、104.建造最大岛屿
文章目录 101.孤岛的总面积思路与重点 102.沉没孤岛思路与重点 103.水流问题思路与重点 104.建造最大岛屿思路与重点 101.孤岛的总面积 题目链接:101.孤岛的总面积讲解链接:代码随想录状态:直接看题解了。 思路与重点 nextx或者nexty越界了…...
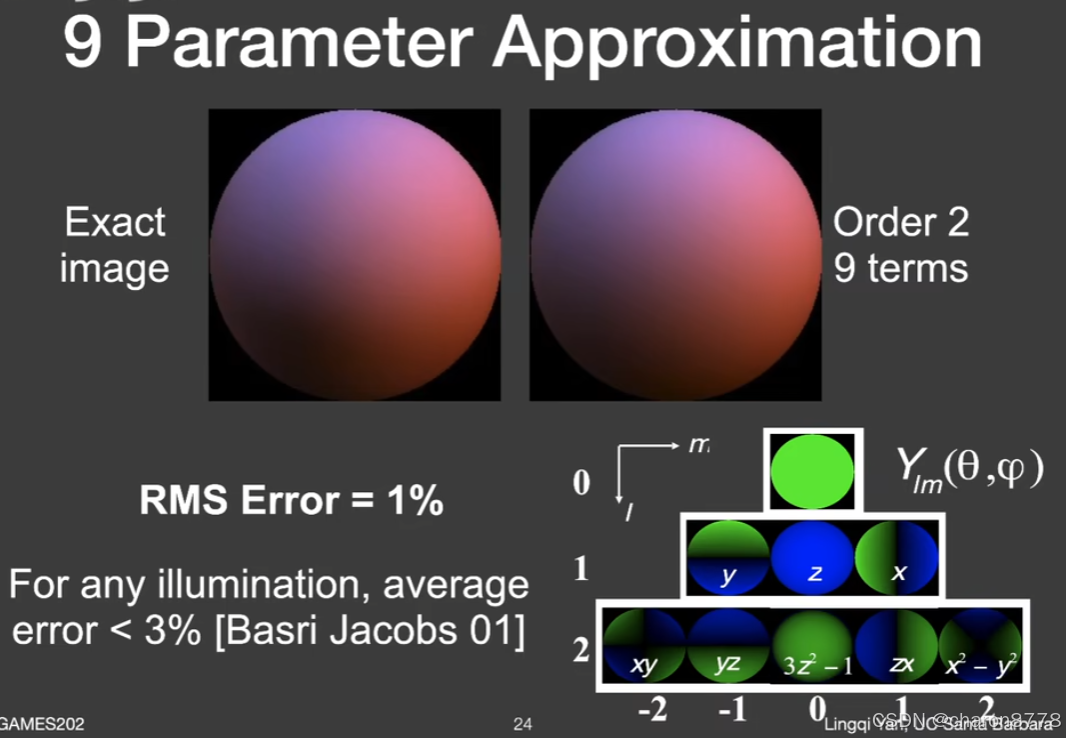
Games202Lecture 6 Real-time Environment Mapping
RTRT RTRT(real time ray tracing): path tracingdenoising PRT PRT (Precomputed radiance transfer):离线预计算,运行时快速内积。 预计算(Offline Precomputation): 传输函数(Transfer Function&…...

在 Zemax 中使用布尔对象创建光学光圈
在 Zemax 中,布尔对象用于通过组合或减去较简单的几何形状来创建复杂形状。布尔运算涉及使用集合运算(如并集、交集和减集)来组合或修改对象的几何形状。这允许用户在其设计中为光学元件或机械部件创建更复杂和定制的形状。 本视频中…...
)
MySQL知识点总结(十八)
说明你对InnoDB集群的整体认知。 MySQL组复制技术是InnoDB集群实现的基础,组复制安装在集群中的每个服务器实例上。组复制能够创建弹性复制拓扑,在集群中的服务器脱机时可以自动重新配置自己。必须至少有三台服务器才能组成一个可以提供高可用性的组。组…...

[论文总结] 深度学习在农业领域应用论文笔记14
当下,深度学习在农业领域的研究热度持续攀升,相关论文发表量呈现出迅猛增长的态势。但繁荣背后,质量却不尽人意。相当一部分论文内容空洞无物,缺乏能够落地转化的实际价值,“凑数” 的痕迹十分明显。在农业信息化领域的…...

MySQL和Redis的区别
MySQL和Redis都是流行的数据存储解决方案,但它们在设计、用途和特性上有显著区别。理解这些区别有助于选择合适的数据库来满足不同的应用需求。本文将详细介绍MySQL和Redis的区别,包括它们的架构、使用场景、性能和其他关键特性。 一、基本概述 MySQL&…...

Rust 中的注释使用指南
Rust 中的注释使用指南 注释是代码中不可或缺的一部分,它帮助开发者理解代码的逻辑和意图。Rust 提供了多种注释方式,包括行注释、块注释和文档注释。本文将详细介绍这些注释的使用方法,并通过一个示例展示如何在实际代码中应用注释。 1. 行…...
)
2025年2月2日(tcp3次握手4次挥手)
TCP(三次握手和四次挥手)是建立和关闭网络连接的标准过程,确保数据在传输过程中可靠无误。下面是详细解释: 1. 三次握手(TCP连接建立过程) 三次握手是为了在客户端和服务器之间建立一个可靠的连接&#x…...

一文了解制造业中的QC是什么
制造业中的QC QC :Quality Control,品质控制,产品的质量检验,发现质量问题后的分析、改善和不合格品控制相关人员的总称。中文意思是品质控制、质量检验。为达到品质要求所采取的作业技术和活动。有些推行ISO9000的组织会设置这样…...

【NEXT】网络编程——上传文件(不限于jpg/png/pdf/txt/doc等),或请求参数值是file类型时,调用在线服务接口
最近在使用华为AI平台ModelArts训练自己的图像识别模型,并部署了在线服务接口。供给客户端(如:鸿蒙APP/元服务)调用。 import核心能力: import { http } from kit.NetworkKit; import { fileIo } from kit.CoreFileK…...

在CentOS服务器上部署DeepSeek R1
在CentOS服务器上部署DeepSeek R1,并通过公网IP与其进行对话,可以按照以下步骤操作: 一、环境准备 系统要求: CentOS 8+(需支持AVX512指令集)。 硬件配置: GPU版本:NVIDIA驱动520+,CUDA 11.8+。 CPU版本:至少16核处理器,64GB内存。 存储空间:原始模型需要30GB,量…...

算法随笔_36: 复写零
上一篇:算法随笔_35: 每日温度-CSDN博客 题目描述如下: 给你一个长度固定的整数数组 arr ,请你将该数组中出现的每个零都复写一遍,并将其余的元素向右平移。 注意:请不要在超过该数组长度的位置写入元素。请对输入的数组 就地 进行上述修改…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...

mac:大模型系列测试
0 MAC 前几天经过学生优惠以及国补17K入手了mac studio,然后这两天亲自测试其模型行运用能力如何,是否支持微调、推理速度等能力。下面进入正文。 1 mac 与 unsloth 按照下面的进行安装以及测试,是可以跑通文章里面的代码。训练速度也是很快的。 注意…...
)
华为OD最新机试真题-数组组成的最小数字-OD统一考试(B卷)
题目描述 给定一个整型数组,请从该数组中选择3个元素 组成最小数字并输出 (如果数组长度小于3,则选择数组中所有元素来组成最小数字)。 输入描述 行用半角逗号分割的字符串记录的整型数组,0<数组长度<= 100,0<整数的取值范围<= 10000。 输出描述 由3个元素组成…...
