编程题-电话号码的字母组合(中等)
题目:
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。


解法一(哈希表+动态添加):
将电话号码中数字到字母的映射保存至哈希表中,遍历输入digits字符串中的每个字符,逐个添加所有等可能的组合情况,如下为笔者代码:
class Solution {
public:vector<string> letterCombinations(string digits) {int length = digits.size();vector<string> result;unordered_map<char, string> hashTable1;hashTable1['1'] = "";hashTable1['2'] = "abc";hashTable1['3'] = "def";hashTable1['4'] = "ghi";hashTable1['5'] = "jkl";hashTable1['6'] = "mno";hashTable1['7'] = "pqrs";hashTable1['8'] = "tuv";hashTable1['9'] = "wxyz";//遍历digits字符串中的所有字符for(char c:digits){string s = hashTable1[c];if(result.empty() && s!=""){for(char cc:s){string in_string(1, cc);result.push_back(in_string);}continue;}if(s!=""){int a = result.size();int b = s.size();//根据已有result容器中的字符串结果和此时输入数字对应的字符串字母s,确定容器中新增的字符串for(int i =0; i<b-1; i++){for(int j=0; j<a; j++){result.push_back(result[j]);}}int num = 0;//遍历字符串s,将字符串s中字符与result中现存字符串进行组合,更新得到添加后的新字符串for(char d:s){for(int i=0; i<a; i++){result[num+i] = result[num+i]+d;}num += a;}}}return result;}
};解法二(回溯算法):
首先使用哈希表存储每个数字对应的所有可能的字母,然后进行回溯操作。
回溯过程中维护一个字符串,表示已有的字母排列(如果未遍历完电话号码的所有数字,则已有的字母排列是不完整的)。该字符串初始为空,每次取电话号码的一位数字,从哈希表中获得该数字对应的所有可能的字母,并将其中的一个字母插入到已有的字母排列的后面,然后继续处理电话号码的后一位数字,直到处理完电话号码中的所有数字,即得到一个完整的字母排列。然后进行回退操作,遍历其余的字母排列。
回溯算法用于寻找所有的可行解,如果发现一个解不可行,则会舍弃不可行的解。在这道题中,由于每个数字对应的每个字母都可能进入字母组合,因此不存在不可行的解,直接穷举所有的解即可。实现代码如下所示:
class Solution {
public:vector<string> letterCombinations(string digits) {vector<string> combinations;if (digits.empty()) {return combinations;}unordered_map<char, string> phoneMap{{'2', "abc"},{'3', "def"},{'4', "ghi"},{'5', "jkl"},{'6', "mno"},{'7', "pqrs"},{'8', "tuv"},{'9', "wxyz"}};string combination;backtrack(combinations, phoneMap, digits, 0, combination);return combinations;}void backtrack(vector<string>& combinations, const unordered_map<char, string>& phoneMap, const string& digits, int index, string& combination) {if (index == digits.length()) {combinations.push_back(combination);} else {char digit = digits[index];const string& letters = phoneMap.at(digit);for (const char& letter: letters) {//添加string字符串类型的combination最顶部的那个字符元素combination.push_back(letter);//调用递归函数,进行枚举遍历(终止条件是index索引值==digits字符串长度)backtrack(combinations, phoneMap, digits, index + 1, combination);//去除string字符串类型的combination最顶部的那个字符元素combination.pop_back();}}}
};时间复杂度:O(3m×4n),其中 m 是输入中对应 3 个字母的数字个数(包括数字 2、3、4、5、6、8),n 是输入中对应 4 个字母的数字个数(包括数字 7、9),m+n 是输入数字的总个数。当输入包含 m 个对应 3 个字母的数字和 n 个对应 4 个字母的数字时,不同的字母组合一共有 3m×4n 种,需要遍历每一种字母组合。空间复杂度:O(m+n),其中 m 是输入中对应 3 个字母的数字个数,n 是输入中对应 4 个字母的数字个数,m+n 是输入数字的总个数。除了返回值以外,空间复杂度主要取决于哈希表以及回溯过程中的递归调用层数,哈希表的大小与输入无关,可以看成常数,递归调用层数最大为 m+n。
笔者小记:
1、vector<string>& combinations;const unordered_map<char, string>& phoneMap;const string& digits;string& combination中 “&” 符号表示传递的引用,数据对象本身可以随着引用值的修改一起修改。
2、combination.pop_back()中的.pop_back()函数,表示将conbination字符串类型的对象去除容器顶部的一个字符类型元素。
3、递归与回溯的区别:在函数中调用自身的方法称为递归,递归函数需要确定递归函数的参数和返回值、确定递归函数的终止条件,确定单层递归的逻辑(确定每一层递归需要处理的信息,在这里也会重复调用自己来实现递归的过程)。回溯函数可以理解成多分支的递归,主要是递归+局部暴力枚举来实现(回溯有剪枝的功能,去掉那些不必要的递归)。回溯算法需要确定回溯函数模版返回值以及参数,回溯函数终止条件,回溯搜索的遍历过程【(回溯法一般是在集合中递归搜索(for循环,一个节点有多少个孩子,就执行多少次),集合的大小构成了树的宽度,递归的深度构成了树的深度)】
相关文章:

编程题-电话号码的字母组合(中等)
题目: 给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。 给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。 解法一(哈希表动态添加)&#x…...

EasyExcel使用详解
文章目录 EasyExcel使用详解一、引言二、环境准备与基础配置1、添加依赖2、定义实体类 三、Excel 读取详解1、基础读取2、自定义监听器3、多 Sheet 处理 四、Excel 写入详解1、基础写入2、动态列与复杂表头3、样式与模板填充 五、总结 EasyExcel使用详解 一、引言 EasyExcel 是…...
:强化学习中基于策略(Policy-Based)和基于价值(Value-Based)方法的区别)
基于“蘑菇书”的强化学习知识点(二):强化学习中基于策略(Policy-Based)和基于价值(Value-Based)方法的区别
强化学习中基于策略(Policy-Based)和基于价值(Value-Based)方法的区别 摘要强化学习中基于策略(Policy-Based)和基于价值(Value-Based)方法的区别1. 定义与核心思想(1) 基于策略的方…...

民法学学习笔记(个人向) Part.2
民法学学习笔记(个人向) Part.2 民法始终在解决两个生活中的核心问题: 私法自治;交易安全; 3. 自然人 3.4 个体工商户、农村承包经营户 都是特殊的个体经济单位; 3.4.1 个体工商户 是指在法律的允许范围内,依法经…...

物业管理系统源码驱动社区管理革新提升用户满意度与服务效率
内容概要 在当今社会,物业管理正面临着前所未有的挑战,尤其是在社区管理方面。人们对社区安全、环境卫生、设施维护等日常生活需求愈发重视,物业公司必须提升服务质量,以满足居民日益增长的期望。而物业管理系统源码的出现&#…...

租房管理系统助力数字化转型提升租赁服务质量与用户体验
内容概要 随着信息技术的快速发展,租房管理系统正逐渐成为租赁行业数字化转型的核心工具。通过全面集成资产管理、租赁管理和物业管理等功能,这种系统力求为用户提供高效便捷的服务体验。无论是工业园、产业园还是写字楼、公寓,租房管理系统…...

Ollama教程:轻松上手本地大语言模型部署
Ollama教程:轻松上手本地大语言模型部署 在大语言模型(LLM)飞速发展的今天,越来越多的开发者希望能够在本地部署和使用这些模型,以便更好地控制数据隐私和计算资源。Ollama作为一个开源工具,旨在简化大语言…...

Baklib推动数字化内容管理解决方案助力企业数字化转型
内容概要 在当今信息爆炸的时代,数字化内容管理成为企业提升效率和竞争力的关键。企业在面对大量数据时,如何高效地存储、分类与检索信息,直接关系到其经营的成败。数字化内容管理不仅限于简单的文档存储,更是整合了文档、图像、…...

DeepSeek-R1 论文. Reinforcement Learning 通过强化学习激励大型语言模型的推理能力
论文链接: [2501.12948] DeepSeek-R1: Incentivizing Reasoning Capability in LLMs via Reinforcement Learning 实在太长,自行扔到 Model 里,去翻译去提问吧。 工作原理: 主要技术,就是训练出一些专有用途小模型&…...

DOM 操作入门:HTML 元素操作与页面事件处理
DOM 操作入门:HTML 元素操作与页面事件处理 DOM 操作入门:HTML 元素操作与页面事件处理什么是 DOM?1. 如何操作 HTML 元素?1.1 使用 `document.getElementById()` 获取单个元素1.2 使用 `document.querySelector()` 和 `document.querySelectorAll()` 获取多个元素1.3 创建…...

使用 HTTP::Server::Simple 实现轻量级 HTTP 服务器
在Perl中,HTTP::Server::Simple 模块提供了一种轻量级的方式来实现HTTP服务器。该模块简单易用,适合快速开发和测试HTTP服务。本文将详细介绍如何使用 HTTP::Server::Simple 模块创建和配置一个轻量级HTTP服务器。 安装 HTTP::Server::Simple 首先&…...

C++滑动窗口技术深度解析:核心原理、高效实现与高阶应用实践
目录 一、滑动窗口的核心原理 二、滑动窗口的两种类型 1. 固定大小的窗口 2. 可变大小的窗口 三、实现细节与关键点 1. 窗口的初始化 2. 窗口的移动策略 3. 结果的更新时机 四、经典问题与代码示例 示例 1:和 ≥ target 的最短子数组(可变窗口…...

基于构件的软件开发方法
摘要: 本人在2023年1月参与广东某公司委托我司开发的“虚拟电厂”项目,主要负责整体架构设计和中间件的选型,该项目为新型电力存储、电力调度、能源交易提供一整套的软件系统,包括设备接入、负载预测、邀约竞价、用户设备调控等功能。本项目以“虚拟电厂”项目为例,讨论基…...

网站快速收录:如何设置robots.txt文件?
本文转自:百万收录网 原文链接:https://www.baiwanshoulu.com/34.html 为了网站快速收录而合理设置robots.txt文件,需要遵循一定的规则和最佳实践。robots.txt文件是一个纯文本文件,它告诉搜索引擎爬虫哪些页面可以访问ÿ…...
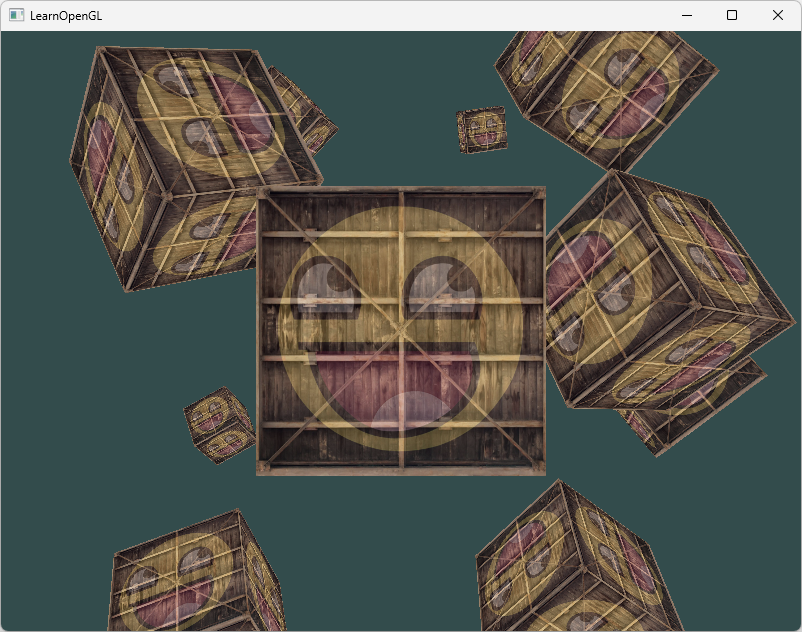
OpenGL学习笔记(六):Transformations 变换(变换矩阵、坐标系统、GLM库应用)
文章目录 向量变换使用GLM变换(缩放、旋转、位移)将变换矩阵传递给着色器坐标系统与MVP矩阵三维变换绘制3D立方体 & 深度测试(Z-buffer)练习1——更多立方体 现在我们已经知道了如何创建一个物体、着色、加入纹理。但它们都还…...

8.攻防世界Web_php_wrong_nginx_config
进入题目页面如下 尝试弱口令密码登录 一直显示网站建设中,尝试无果,查看源码也没有什么特别漏洞存在 用Kali中的dirsearch扫描根目录试试 命令: dirsearch -u http://61.147.171.105:53736/ -e* 登录文件便是刚才登录的界面打开robots.txt…...

【优先算法】专题——位运算
在讲解位运算之前我们来总结一下常见的位运算 一、常见的位运算 1.基础为运算 << &:有0就是0 >> |:有1就是1 ~ ^:相同为0,相异位1 /无进位相加 2.给一个数 n,确定它的二进制表示…...

qt.qpa.plugin: Could not find the Qt platform plugin “dxcb“ in ““
个人博客地址:qt.qpa.plugin: Could not find the Qt platform plugin "dxcb" in "" | 一张假钞的真实世界 我遇到的场景是,在Deepin系统终端中运行PySide应用时,没有错误提示,但在VS Code中运行时ÿ…...

1-刷力扣问题记录
25.1.19 1.size()和.length()有什么区别 2.result.push_back({nums[i], nums[left], nums[right]});为什么用大括号? 使用大括号 {} 是 C11 引入的 初始化列表 语法,它允许我们在构造或初始化对象时直接传入一组值。大括号的使用在许多情况下都能让代码…...

物联网 STM32【源代码形式-使用以太网】连接OneNet IOT从云产品开发到底层MQTT实现,APP控制 【保姆级零基础搭建】
物联网(IoT)是指通过各种信息传感器、射频识别技术、全球定位系统、红外感应器等装置与技术,实时采集并连接任何需要监控、连接、互动的物体或过程,实现对物品和过程的智能化感知、识别和管理。物联网的核心功能包括数据采集与监…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

xmind转换为markdown
文章目录 解锁思维导图新姿势:将XMind转为结构化Markdown 一、认识Xmind结构二、核心转换流程详解1.解压XMind文件(ZIP处理)2.解析JSON数据结构3:递归转换树形结构4:Markdown层级生成逻辑 三、完整代码 解锁思维导图新…...

【HarmonyOS 5】鸿蒙中Stage模型与FA模型详解
一、前言 在HarmonyOS 5的应用开发模型中,featureAbility是旧版FA模型(Feature Ability)的用法,Stage模型已采用全新的应用架构,推荐使用组件化的上下文获取方式,而非依赖featureAbility。 FA大概是API7之…...

JDK 17 序列化是怎么回事
如何序列化?其实很简单,就是根据每个类型,用工厂类调用。逐个完成。 没什么漂亮的代码,只有有效、稳定的代码。 代码中调用toJson toJson 代码 mapper.writeValueAsString ObjectMapper DefaultSerializerProvider 一堆实…...

车载诊断架构 --- ZEVonUDS(J1979-3)简介第一篇
我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 做到欲望极简,了解自己的真实欲望,不受外在潮流的影响,不盲从,不跟风。把自己的精力全部用在自己。一是去掉多余,凡事找规律,基础是诚信;二是…...
