脉冲信号傅里叶变换与频域分析:从计算到理解
摘要
本文聚焦于脉冲信号的傅里叶变换,详细推导了矩形脉冲信号和单边指数信号的傅里叶变换过程,深入解释了傅里叶变换结果 F ( ω ) F(\omega) F(ω) 的内涵,包括其定义、物理意义、包含的信息以及在实际应用中的重要性。旨在帮助读者全面掌握脉冲信号在时域和频域之间的转换,以及频域分析在信号处理中的关键作用。
一、引言
在信号处理、通信、物理等众多领域中,信号的分析与处理至关重要。傅里叶变换作为一种强大的数学工具,能够将信号从时域转换到频域,揭示信号的频率特性,为信号的处理、滤波、调制等操作提供了有力支持。脉冲信号是一类常见且具有重要应用价值的信号,研究其傅里叶变换过程及频域表示 F ( ω ) F(\omega) F(ω) 具有重要意义。

二、脉冲信号傅里叶变换计算
2.1 矩形脉冲信号的傅里叶变换
2.1.1 矩形脉冲信号定义
矩形脉冲信号 f ( t ) f(t) f(t) 定义为:
f ( t ) = { A , ∣ t ∣ ≤ τ 2 0 , ∣ t ∣ > τ 2 f(t)=\begin{cases} A, & |t|\leq\frac{\tau}{2}\\ 0, & |t|>\frac{\tau}{2} \end{cases} f(t)={A,0,∣t∣≤2τ∣t∣>2τ
其中 A A A 为脉冲幅度, τ \tau τ 为脉冲宽度。
2.1.2 傅里叶变换推导
根据傅里叶变换定义 F ( ω ) = ∫ − ∞ ∞ f ( t ) e − j ω t d t F(\omega)=\int_{-\infty}^{\infty}f(t)e^{-j\omega t}dt F(ω)=∫−∞∞f(t)e−jωtdt由于 f ( t ) f(t) f(t) 在 ∣ t ∣ > τ 2 |t|>\frac{\tau}{2} ∣t∣>2τ 时为 0 0 0,则:
F ( ω ) = ∫ − τ 2 τ 2 A e − j ω t d t F(\omega)=\int_{-\frac{\tau}{2}}^{\frac{\tau}{2}}Ae^{-j\omega t}dt F(ω)=∫−2τ2τAe−jωtdt
利用指数函数积分公式 ∫ e a x d x = 1 a e a x + C ( a ≠ 0 ) \int e^{ax}dx=\frac{1}{a}e^{ax}+C(a\neq0) ∫eaxdx=a1eax+C(a=0) 可得:
F ( ω ) = A [ e − j ω t − j ω ] − τ 2 τ 2 = A − j ω ( e − j ω τ 2 − e j ω τ 2 ) \begin{align*} F(\omega)&=A\left[\frac{e^{-j\omega t}}{-j\omega}\right]_{-\frac{\tau}{2}}^{\frac{\tau}{2}}\\ &=\frac{A}{-j\omega}(e^{-j\frac{\omega\tau}{2}} - e^{j\frac{\omega\tau}{2}}) \end{align*} F(ω)=A[−jωe−jωt]−2τ2τ=−jωA(e−j2ωτ−ej2ωτ)
由欧拉公式 e j θ = cos θ + j sin θ e^{j\theta}=\cos\theta + j\sin\theta ejθ=cosθ+jsinθ e − j θ = cos θ − j sin θ e^{-j\theta}=\cos\theta - j\sin\theta e−jθ=cosθ−jsinθ 可知 e − j ω τ 2 − e j ω τ 2 = − 2 j sin ( ω τ 2 ) e^{-j\frac{\omega\tau}{2}} - e^{j\frac{\omega\tau}{2}}=-2j\sin(\frac{\omega\tau}{2}) e−j2ωτ−ej2ωτ=−2jsin(2ωτ)所以:
F ( ω ) = A τ sin ( ω τ 2 ) ω τ 2 = A τ S a ( ω τ 2 ) F(\omega)=A\tau\frac{\sin(\frac{\omega\tau}{2})}{\frac{\omega\tau}{2}} = A\tau Sa(\frac{\omega\tau}{2}) F(ω)=Aτ2ωτsin(2ωτ)=AτSa(2ωτ)
其中 S a ( x ) = sin x x Sa(x)=\frac{\sin x}{x} Sa(x)=xsinx 为抽样函数,曲线如下:

2.1.3 频谱特性分析
- 幅度谱:幅度谱 ∣ F ( ω ) ∣ = ∣ A τ S a ( ω τ 2 ) ∣ |F(\omega)| = |A\tau Sa(\frac{\omega\tau}{2})| ∣F(ω)∣=∣AτSa(2ωτ)∣在 ω = 0 \omega = 0 ω=0 处取得最大值 A τ A\tau Aτ。随着 ∣ ω ∣ |\omega| ∣ω∣ 增大,函数值振荡衰减,第一个零点位于 ω = ± 2 π τ \omega=\pm\frac{2\pi}{\tau} ω=±τ2π。主瓣( − 2 π τ -\frac{2\pi}{\tau} −τ2π 到 2 π τ \frac{2\pi}{\tau} τ2π 区间)包含主要能量,主瓣宽度为 4 π τ \frac{4\pi}{\tau} τ4π 。
- 带宽:通常将主瓣宽度定义为信号带宽 B = 2 π τ B=\frac{2\pi}{\tau} B=τ2π(角频率),对应的频率带宽 f = 1 τ f = \frac{1}{\tau} f=τ1,表明脉冲宽度越窄,信号带宽越宽。
2.2 单边指数信号的傅里叶变换
2.2.1 单边指数信号定义
单边指数信号 f ( t ) f(t) f(t) 表达式为:
f ( t ) = { e − α t , t ≥ 0 , α > 0 0 , t < 0 f(t)=\begin{cases} e^{-\alpha t}, & t\geq0,\alpha>0\\ 0, & t < 0 \end{cases} f(t)={e−αt,0,t≥0,α>0t<0
其中 α \alpha α 为控制信号衰减速度的正常数。
2.2.2 傅里叶变换推导
将 f ( t ) f(t) f(t) 代入傅里叶变换公式,因 t < 0 t < 0 t<0 时 f ( t ) = 0 f(t)=0 f(t)=0,有:
F ( ω ) = ∫ 0 ∞ e − α t e − j ω t d t = ∫ 0 ∞ e − ( α + j ω ) t d t F(\omega)=\int_{0}^{\infty}e^{-\alpha t}e^{-j\omega t}dt=\int_{0}^{\infty}e^{-(\alpha + j\omega)t}dt F(ω)=∫0∞e−αte−jωtdt=∫0∞e−(α+jω)tdt
根据积分公式计算:
F ( ω ) = [ − 1 α + j ω e − ( α + j ω ) t ] 0 ∞ = lim b → ∞ ( − 1 α + j ω e − ( α + j ω ) b ) − ( − 1 α + j ω e − ( α + j ω ) × 0 ) \begin{align*} F(\omega)&=\left[-\frac{1}{\alpha + j\omega}e^{-(\alpha + j\omega)t}\right]_{0}^{\infty}\\ &=\lim_{b\rightarrow\infty}\left(-\frac{1}{\alpha + j\omega}e^{-(\alpha + j\omega)b}\right)-\left(-\frac{1}{\alpha + j\omega}e^{-(\alpha + j\omega)\times0}\right) \end{align*} F(ω)=[−α+jω1e−(α+jω)t]0∞=b→∞lim(−α+jω1e−(α+jω)b)−(−α+jω1e−(α+jω)×0)
由于 α > 0 \alpha>0 α>0, lim b → ∞ e − ( α + j ω ) b = 0 \lim_{b\rightarrow\infty}e^{-(\alpha + j\omega)b}=0 b→∞lime−(α+jω)b=0 e − ( α + j ω ) × 0 = 1 e^{-(\alpha + j\omega)\times0}=1 e−(α+jω)×0=1所以 F ( ω ) = 1 α + j ω F(\omega)=\frac{1}{\alpha + j\omega} F(ω)=α+jω1
进一步化简,分子分母同乘 α − j ω \alpha - j\omega α−jω 得:
F ( ω ) = α − j ω α 2 + ω 2 = α α 2 + ω 2 − j ω α 2 + ω 2 \begin{align*} F(\omega)&=\frac{\alpha - j\omega}{\alpha^{2}+\omega^{2}}\\ &=\frac{\alpha}{\alpha^{2}+\omega^{2}}-j\frac{\omega}{\alpha^{2}+\omega^{2}} \end{align*} F(ω)=α2+ω2α−jω=α2+ω2α−jα2+ω2ω
2.2.3 频谱特性分析
- 幅度谱: ∣ F ( ω ) ∣ = 1 α 2 + ω 2 |F(\omega)|=\frac{1}{\sqrt{\alpha^{2}+\omega^{2}}} ∣F(ω)∣=α2+ω21随 ∣ ω ∣ |\omega| ∣ω∣ 增大而减小, ω = 0 \omega = 0 ω=0 时, ∣ F ( 0 ) ∣ = 1 α |F(0)|=\frac{1}{\alpha} ∣F(0)∣=α1。
- 相位谱: φ ( ω ) = − arctan ( ω α ) \varphi(\omega)=-\arctan(\frac{\omega}{\alpha}) φ(ω)=−arctan(αω)单边指数信号频谱在整个频率轴分布,低频成分比重相对较大。
三、对 F ( ω ) F(\omega) F(ω) 的深入理解
3.1 F ( ω ) F(\omega) F(ω) 的定义与本质
F ( ω ) F(\omega) F(ω) 是时域信号 f ( t ) f(t) f(t) 通过傅里叶正变换得到的频域表示,其定义式 F ( ω ) = ∫ − ∞ ∞ f ( t ) e − j ω t d t F(\omega)=\int_{-\infty}^{\infty}f(t)e^{-j\omega t}dt F(ω)=∫−∞∞f(t)e−jωtdt 是一个积分运算,将时域信号分解为不同频率的复指数信号叠加,每个频率分量的权重由 F ( ω ) F(\omega) F(ω) 确定。
3.2 F ( ω ) F(\omega) F(ω) 的物理意义
从物理角度看,傅里叶变换将复杂时域信号分解为一系列不同频率的正弦或余弦信号(或复指数信号)叠加。 F ( ω ) F(\omega) F(ω) 反映了信号在各个频率分量上的分布情况。例如,对于音频信号,时域信号 f ( t ) f(t) f(t) 描述声音随时间的强弱变化,频域信号 F ( ω ) F(\omega) F(ω) 则展示声音包含的音调频率及各音调强度。
3.3 F ( ω ) F(\omega) F(ω) 包含的信息
3.3.1 幅度谱
F ( ω ) F(\omega) F(ω) 一般为复数,可表示为 F ( ω ) = ∣ F ( ω ) ∣ e j φ ( ω ) F(\omega)=|F(\omega)|e^{j\varphi(\omega)} F(ω)=∣F(ω)∣ejφ(ω)其中 ∣ F ( ω ) ∣ |F(\omega)| ∣F(ω)∣ 是幅度谱,描述不同频率分量的幅度大小。如矩形脉冲信号和单边指数信号的幅度谱,直观展示了信号在不同频率下的强度分布。
3.3.2 相位谱
φ ( ω ) \varphi(\omega) φ(ω) 是相位谱,描述不同频率分量的相位信息。相位决定每个频率分量的起始位置,对信号合成和波形恢复至关重要。多个正弦波合成复杂信号时,各正弦波相位不同,合成波形也不同。
3.4 F ( ω ) F(\omega) F(ω) 在实际应用中的价值
3.4.1 信号滤波
在信号处理中,通过分析 F ( ω ) F(\omega) F(ω) 的幅度谱确定噪声所在频率范围,设计合适滤波器。如噪声集中在高频段,设计低通滤波器让低频信号通过,阻挡高频噪声,实现信号滤波处理。
3.4.2 通信系统
在通信领域,调制和解调是关键环节。通过对信号频域分析(即分析 F ( ω ) F(\omega) F(ω) ),了解调制前后信号频率特性变化,优化调制和解调方案,提高通信系统性能。
3.4.3 图像处理
在图像处理中,二维傅里叶变换将图像从空间域转换到频域。图像低频成分对应整体轮廓和缓慢变化部分,高频成分对应细节和边缘信息。对图像频域信号处理,如增强高频成分使图像更清晰锐利,去除高频噪声使图像更平滑。
四、结论
本文详细推导了矩形脉冲信号和单边指数信号的傅里叶变换过程,深入解释了傅里叶变换结果 F ( ω ) F(\omega) F(ω) 的内涵。傅里叶变换作为连接时域和频域的桥梁,使我们能够从频率角度深入分析信号特性。通过对 F ( ω ) F(\omega) F(ω) 的幅度谱和相位谱分析,我们可以了解信号的频率成分分布和相位关系,进而在信号滤波、通信系统设计、图像处理等实际应用中发挥重要作用。掌握脉冲信号的傅里叶变换及频域分析方法,有助于我们更好地处理和理解各种复杂信号。
相关文章:

脉冲信号傅里叶变换与频域分析:从计算到理解
摘要 本文聚焦于脉冲信号的傅里叶变换,详细推导了矩形脉冲信号和单边指数信号的傅里叶变换过程,深入解释了傅里叶变换结果 F ( ω ) F(\omega) F(ω) 的内涵,包括其定义、物理意义、包含的信息以及在实际应用中的重要性。旨在帮助读者全面掌…...

6.【BUUCTF】[SUCTF 2019]CheckIn
打开题目页面如下 看样子是一道有关文件上传的题 上传一句话木马 显示:非法后缀! 看来.php后缀被过滤了 上传一张带有木马的照片 在文件地址处输入cmd 输入以下代码执行 copy 1.jpg/b4.php/a 5.jpg 最后一行有一句话木马 上传带有木马的图片 但其实…...

基于springboot的体质测试数据分析及可视化设计
作者:学姐 开发技术:SpringBoot、SSM、Vue、MySQL、JSP、ElementUI、Python、小程序等 文末获取“源码数据库万字文档PPT”,支持远程部署调试、运行安装。 项目包含: 完整源码数据库功能演示视频万字文档PPT 项目编码࿱…...

孟加拉国_行政边界省市边界arcgis数据shp格式wgs84坐标
这篇内容将深入探讨孟加拉国的行政边界省市边界数据,该数据是以arcgis的shp格式提供的,并采用WGS84坐标系统。ArcGIS是一款广泛应用于地理信息系统(GIS)的专业软件,它允许用户处理、分析和展示地理空间数据。在GIS领域…...
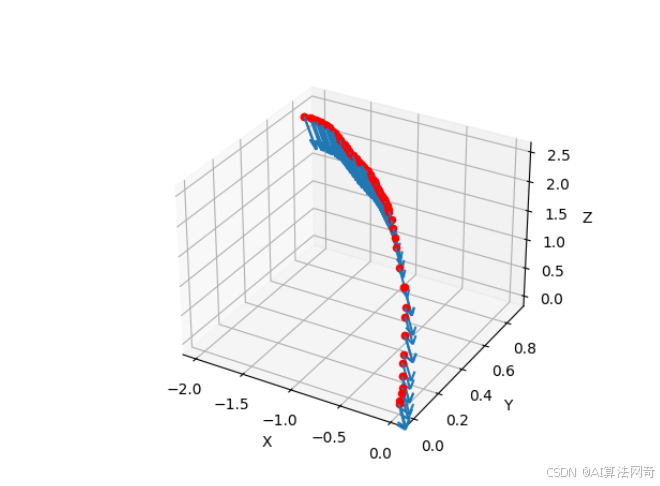
可视化相机pose colmap形式的相机内参外参
目录 内参外参转换 可视化相机pose colmap形式的相机内参外参 内参外参转换 def visualize_cameras(cameras, images):fig plt.figure()ax fig.add_subplot(111, projection3d)for image_id, image_data in images.items():qvec image_data[qvec]tvec image_data[tvec]#…...

数据结构 树2
文章目录 前言 一,二叉搜索树的高度 二,广度优先VS深度优先 三,广度优先的代码实现 四,深度优先代码实现 五,判断是否为二叉搜索树 六,删除一个节点 七,二叉收索树的中序后续节点 总结 …...

GB/T 44721-2024 与 L3 自动驾驶:自动驾驶新时代的基石与指引
1.前言 在智能网联汽车飞速发展的当下,自动驾驶技术成为了行业变革的核心驱动力。从最初的辅助驾驶功能,到如今不断迈向高度自动化的征程,每一步都凝聚着技术的创新与突破。而在这一进程中,标准的制定与完善对于自动驾驶技术的规…...

AURIX TC275学习笔记3 官方例程 (UART LED WDT)
文章目录 参考资料1. ASCLIN_UART_12. GPIO_LED_Button_13. WDT (Watch Dog Timer) 参考资料 AURIX TC275学习笔记1 资料收集Getting Started with AURIX™ Development Studio 官方帮助文档happy hacking for TC275! 硬件平台使用AURIX™ TC275 Lite 套件,按照参…...

Vim的基础命令
移动光标 H(左) J(上) K(下) L(右) $ 表示移动到光标所在行的行尾, ^ 表示移动到光标所在行的行首的第一个非空白字符。 0 表示移动到光标所在行的行首。 W 光标向前跳转一个单词 w光标向前跳转一个单词 B光标向后跳转一个单词 b光标向后跳转一个单词 G 移动光标到…...

Linux的简单使用和部署4asszaaa0
一.部署 1 环境搭建方式主要有四种: 1. 直接安装在物理机上.但是Linux桌面使用起来非常不友好.所以不建议.[不推荐]. 2. 使用虚拟机软件,将Linux搭建在虚拟机上.但是由于当前的虚拟机软件(如VMWare之类的)存在⼀些bug,会导致环境上出现各种莫名其妙的问题比较折腾.[非常不推荐…...

Linux 的 sysfs 伪文件系统介绍【用户可以通过文件操作与内核交互(如调用内核函数),而无需编写内核代码】
1. 什么是 sysfs伪文件系统? sysfs 是 Linux 内核提供的 伪文件系统,用于向用户空间暴露内核对象的信息和控制接口。它是 procfs 的补充,主要用于管理 设备、驱动、内核子系统 等信息,使用户可以通过文件操作(如用户空…...

每日一题洛谷P5721 【深基4.例6】数字直角三角形c++
#include<iostream> using namespace std; int main() {int n;cin >> n;int t 1;for (int i 0; i < n; i) {for (int j 0; j < n - i; j) {printf("%02d",t);t;}cout << endl;}return 0; }...

计算机网络笔记再战——理解几个经典的协议1
目录 前言 从协议是什么出发 关于TCP/IP协议体系 几个传输方式的分类 地址 网卡 中继器(Repeater) 网桥(Bridge) 路由器(Router) 网关 前言 笔者最近正在整理(笔者开的坑不少…...

ElasticSearch学习笔记-解析JSON格式的内容
如果需要屏蔽其他项目对Elasticsearch的直接访问操作,统一由一个入口访问操作Elasticsearch,可以考虑直接传入JSON格式语句解析执行。 相关依赖包 <properties><elasticsearch.version>7.9.3</elasticsearch.version><elasticsea…...
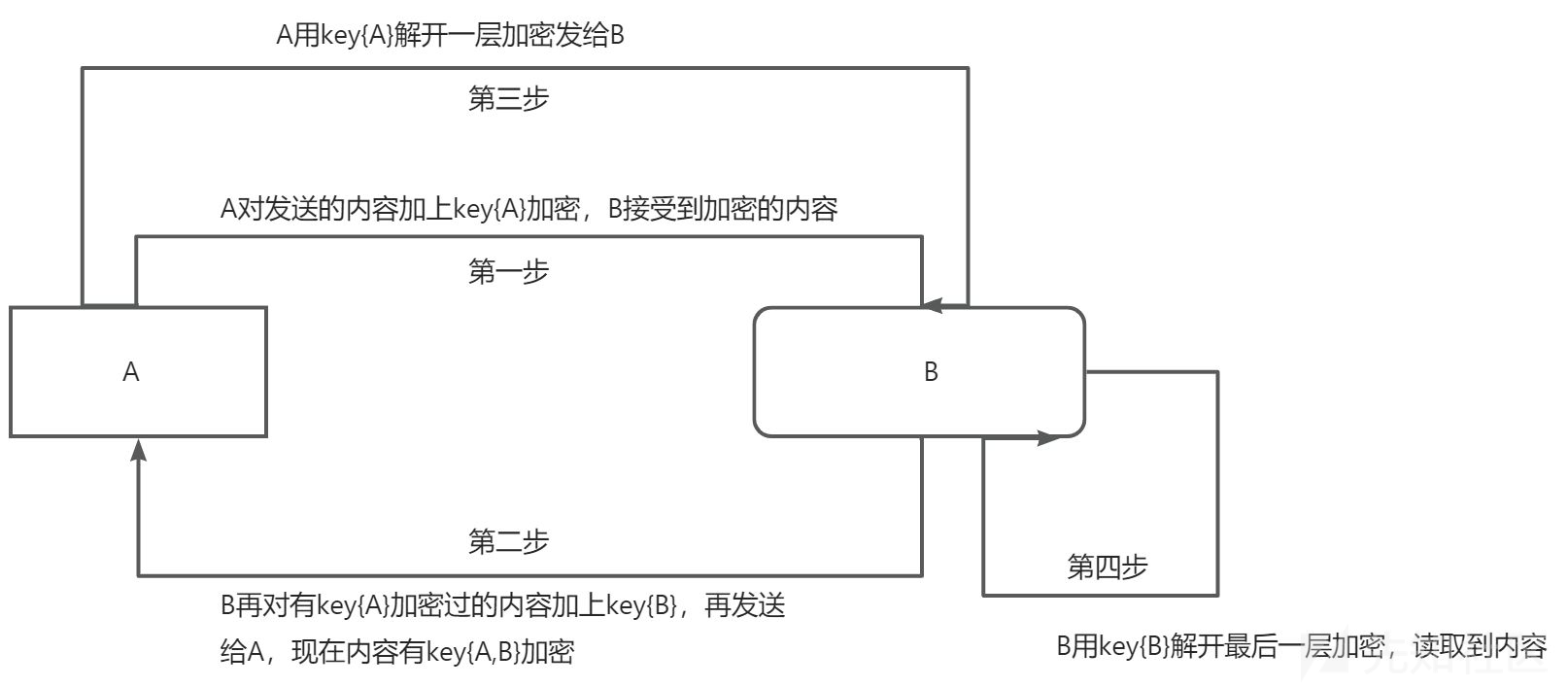
浅谈密码相关原理及代码实现
本代码仅供学习、研究、教育或合法用途。开发者明确声明其无意将该代码用于任何违法、犯罪或违反道德规范的行为。任何个人或组织在使用本代码时,需自行确保其行为符合所在国家或地区的法律法规。 开发者对任何因直接或间接使用该代码而导致的法律责任、经济损失或…...
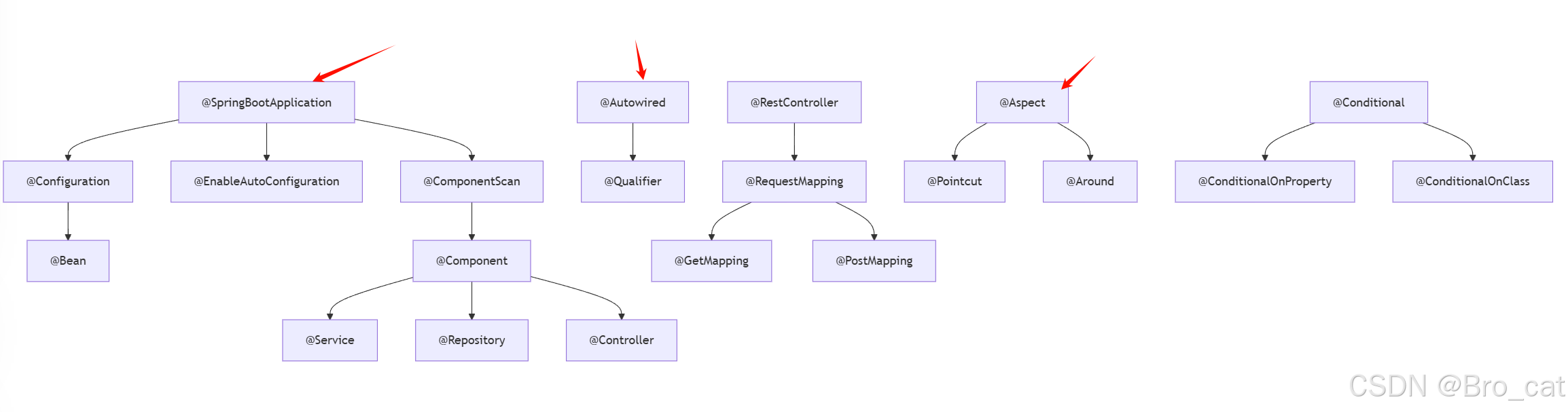
Spring Boot常用注解深度解析:从入门到精通
今天,这篇文章带你将深入理解Spring Boot中30常用注解,通过代码示例和关系图,帮助你彻底掌握Spring核心注解的使用场景和内在联系。 一、启动类与核心注解 1.1 SpringBootApplication 组合注解: SpringBootApplication Confi…...
can not add outlook new accounts on the outlook
link : Reference url...
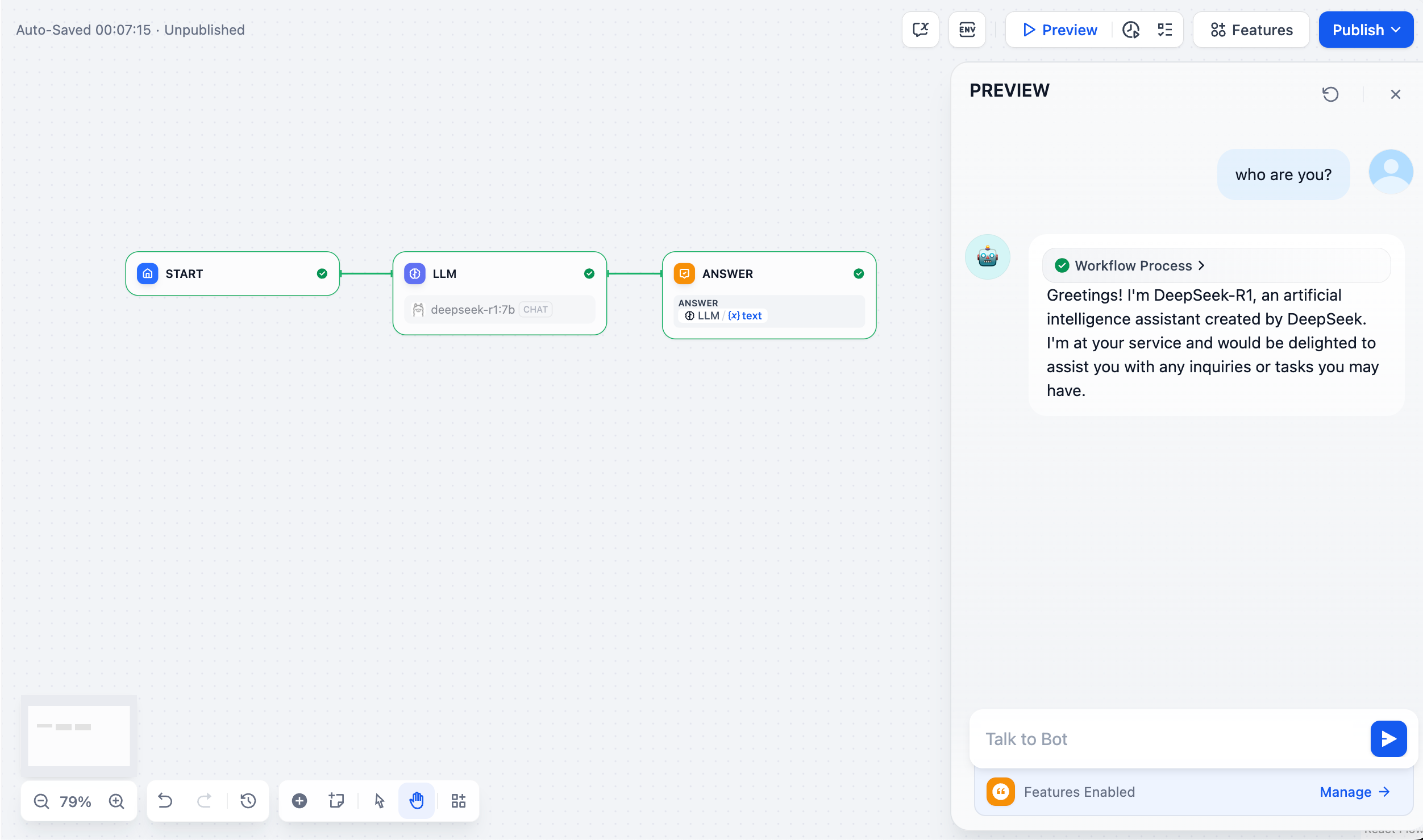
私有化部署 DeepSeek + Dify,构建你的专属私人 AI 助手
私有化部署 DeepSeek Dify,构建你的专属私人 AI 助手 概述 DeepSeek 是一款开创性的开源大语言模型,凭借其先进的算法架构和反思链能力,为 AI 对话交互带来了革新性的体验。通过私有化部署,你可以充分掌控数据安全和使用安全。…...

【Elasticsearch】post_filter
post_filter是 Elasticsearch 中的一种后置过滤机制,用于在查询执行完成后对结果进行过滤。以下是关于post_filter的详细介绍: 工作原理 • 查询后过滤:post_filter在查询执行完毕后对返回的文档集进行过滤。这意味着所有与查询匹配的文档都…...

验证工具:GVIM和VIM
一、定义与关系 gVim:gVim是Vim的图形界面版本,提供了更多的图形化功能,如菜单栏、工具栏和鼠标支持。它使得Vim的使用更加直观和方便,尤其对于不习惯命令行界面的用户来说。Vim:Vim是一个在命令行界面下运行的文本编…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...
