数据结构 树2
文章目录
前言
一,二叉搜索树的高度
二,广度优先VS深度优先
三,广度优先的代码实现
四,深度优先代码实现
五,判断是否为二叉搜索树
六,删除一个节点
七,二叉收索树的中序后续节点
总结
前言
我们上一篇学习了树的基本知识和树的分类,二叉搜索树是作为我们学习的重点内容,所以我将继续深入学习二叉搜索树
一,二叉搜索树的高度
我们来复习一下树的高度和深度
树的高度 节点到子叶节点的距离 树的深度 节点到根节点的距离 接下来我们就要用代码来实现树的高度的计算
#include<iostream>using namespace std;struct BstNode {BstNode* left;int data;BstNode* right; };BstNode* Insert(BstNode* root, int x); BstNode* GetNode(int x); int Hight(BstNode* rtoot);int main() {BstNode* root = NULL;root = Insert(root, 6);root = Insert(root, 9);root = Insert(root, 10);root = Insert(root, 8);root = Insert(root, 4);root = Insert(root, 5);root = Insert(root, 3);int hight = Hight(root);cout << hight << endl; }/*6/ \4 9/ \ / \3 5 8 10 */BstNode* Insert(BstNode* root, int x) {if (root == NULL) {root = GetNode(x);return root;}else if (root->data >= x) {root->left = Insert(root->left, x);}else if (root->data < x) {root->right = Insert(root->right, x);}return root; }BstNode* GetNode(int x) {BstNode* newNode = new BstNode();newNode->data = x;newNode->left = NULL;newNode->right = NULL;return newNode; }int Hight(BstNode* root) {if (root == NULL) {return -1;}int lefthight = Hight(root->left);int righthight = Hight(root->right);return max(lefthight, righthight) + 1; }代码所表示的树的结构图
6/ \4 9/ \ / \ 3 5 8 10代码里的计算高度
int Hight(BstNode* root) {if (root == NULL) {return -1;}int lefthight = Hight(root->left);int righthight = Hight(root->right);return max(lefthight, righthight) + 1; }分析
我们这里如果根节点是空,高度就是-1,这个是规定的
max函数如果没有接触过C++的,这个max是系统自己给的函数,你也可以自己写,就是我们以往写两个数字比较出最大的数字是一样的
递归我们这里用的是递归的方法进行了计算,这里就是不断地寻找NULL的节点,我们拿4的计算为例子
左子树:
- 左子树的根是
33是叶子节点,它没有左子树和右子树,所以它的左右子树的高度都为 0- 那么,
3的高度是max(0, 0) + 1 = 1右子树:
- 右子树的根是
55是叶子节点,它同样没有左右子树- 所以,
5的高度是max(0, 0) + 1 = 1我们不难想出,再寻找NULL的时候,这个是每一个子树的左右子树都是要进行比较的,这个就是递归nb的地方,然后计算完了4,又会跑到右子树进行计算,然后最后把左右两个子树进行比较,这个后面的+1是给子树赋值的
二,广度优先VS深度优先
树不再像我们之前所学的链表,栈,队列这种顺序结构了,它是一个非线性结构,所以树是有属于自己的遍历方法的
在访问树的节点过程中,这个是有先后顺序的,按照某个顺序进行访问,且每个节点只可以访问一次,对于这个遍历,我们有两种方法:1,深度优先 2,广度优先 3,图搜索技术
这个图搜索技术,我们还没有学完图,所以我们值考虑前两个方法1,广度优先思想
我们会逐层访问
1,我们访问第一层,记录9
2,我们访问第二层,记录7,15
3,我们访问第三层,记录4,6,12,16
4,我们访问第四层,记录3,5,14
5,我们访问第五层,记录10
总的次序:9,7,15,4,6,12,16,3,5,14,10先访问同一层次的节点,当访问完这个层次的节点,再到下一深度的层次继续访问
2,深度优先思想
对于这个我们有三种情况
前序 <root><left><right> 中序 <left><root><right> 后序 <left><right><root> 第一个为先访问根,再访问左子树,再访问右子树
顺序:9,7,4,3,5,6,15,12,14,10,16
第二个为先访问左子树,再访问根,再访问右子树
顺序:7,4,3,5,6,9,15,12,14,10,16
第三个为先访问右子树,再访问左子树,再访问根
顺序:7,4,3,5,6,15,12,14,10,16,9就是把子树访问顺序
三,广度优先的代码实现
我们这种逐层的访问不就是很像队列么,先把根放入队列,然后放入孩子,然后把根弹出,再放入孩子的孩子,再把孩子弹出……
接下来我们来实现这个代码
实际我们运行代码,代码会帮我们优化为这样
9/ \7 15/ \ / \4 8 12 16/ \ / \3 5 10 14代码实现
#include<iostream> #include<queue>using namespace std;struct BstNode {BstNode* left;int data;BstNode* right; };BstNode* Insert(BstNode* root, int x); BstNode* GetNode(int x); void leveread(BstNode* root);int main() {BstNode* root = NULL;root = Insert(root, 9); // 根节点root = Insert(root, 7); // 左子树root = Insert(root, 15); // 右子树root = Insert(root, 4); // 7 的左子树root = Insert(root, 8); // 7 的右子树root = Insert(root, 12); // 15 的左子树root = Insert(root, 16); // 15 的右子树root = Insert(root, 3); // 4 的左子树root = Insert(root, 5); // 4 的右子树root = Insert(root, 10); // 12 的左子树root = Insert(root, 14); // 12 的右子树leveread(root); }BstNode* Insert(BstNode* root, int x) {if (root == NULL) {root = GetNode(x);return root;}else if (root->data > x) {root->left = Insert(root->left, x);}else if (root->data < x) {root->right = Insert(root->right, x);}return root; }BstNode* GetNode(int x) {BstNode* newNode = new BstNode();newNode->data = x;newNode->left = NULL;newNode->right = NULL;return newNode; }void leveread(BstNode* root) {if (root == NULL)return;queue<BstNode*>Q;Q.push(root);while (!Q.empty()){BstNode* current = Q.front();cout << current->data << " ";if (current->left!=NULL) {Q.push(current->left);}if (current -> right != NULL) {Q.push(current->right);}Q.pop();} }我们来看这个广度搜索的代码,最后面的函数就是把所有的元素放入到队列里面,然后再进行读取弹出,我们利用队列的顺序,一一的把这个孩子的孩子都放入到队列里面
时间为O(n)
四,深度优先代码实现
前序
9/ \7 15/ \ / \4 8 12 16/ \ / \3 5 10 14代码实现
#include<iostream> #include<queue>using namespace std;struct BstNode {BstNode* left;int data;BstNode* right; };BstNode* Insert(BstNode* root, int x); BstNode* GetNode(int x); void preread(BstNode* root);int main() {BstNode* root = NULL;root = Insert(root, 9); // 根节点root = Insert(root, 7); // 左子树root = Insert(root, 15); // 右子树root = Insert(root, 4); // 7 的左子树root = Insert(root, 8); // 7 的右子树root = Insert(root, 12); // 15 的左子树root = Insert(root, 16); // 15 的右子树root = Insert(root, 3); // 4 的左子树root = Insert(root, 5); // 4 的右子树root = Insert(root, 10); // 12 的左子树root = Insert(root, 14); // 12 的右子树preread(root); }BstNode* Insert(BstNode* root, int x) {if (root == NULL) {root = GetNode(x);return root;}else if (root->data > x) {root->left = Insert(root->left, x);}else if (root->data < x) {root->right = Insert(root->right, x);}return root; }BstNode* GetNode(int x) {BstNode* newNode = new BstNode();newNode->data = x;newNode->left = NULL;newNode->right = NULL;return newNode; }void preread(BstNode* root) {if (root == NULL) {return;}cout << root->data << " ";preread(root->left);preread(root->right); }分析
这个就是把这个cout放到递归上面,为什么呢?如果不知道证明你基础太差了,回炉重造吧,然后进入递归,我们会把左边的全部都找完,因为只要有left为NULL则会返回去找左子树的右子树的值,然后进入的根的左子树的时候,就会跳到根的右子树进行查找,先进去右子树的左子树,然后再进入到右子树的右子树
中序跟后序跟这个前序差不多,这里放了代码,读者可以自行思考
中序
void Inread(BstNode* root) {if (root == NULL) {return;}Inread(root->left);cout << root->data << " ";Inread(root->right); }后序
void proread(BstNode* root) {if (root == NULL) {return;}proread(root->left);proread(root->right);cout << root->data << " "; }时间为O(n)
五,判断是否为二叉搜索树
下面这个代码的时间复杂度为O(n)
bool Isreallytree(BstNode* root,int minvalue,int maxvalue) {if (root == NULL)return true;if (root->data > minvalue&& root->data < maxvalue&& Isreallytree(root->left, minvalue, root->data)&& Isreallytree(root->right, root->data, maxvalue))return true;elsereturn false; }分析
我们再if里面进行不断地判断逻辑梳理
每次我进行递归地时候,先进行左子树的判断,然后对比这个左子树的最大值和最小值,这个最大值每次是需要不断地改进地,就是这个节点,然后当我们地左子树地左边全部判断完了之后,就会执行right语句,也就是去判断这个树地右边进行判断,然后再到根的右子树进行判断,最后决定是返回true还是false
六,删除一个节点
这个东西就比较复杂,因为我们删除之后还要恢复树的平衡
我们把删除的情况分为:1,删除子叶节点 2,删除有两个孩子的节点 3,删除有一个孩子的节点
1,删除子叶节点
我们可以看到,我们可以直接删除即可
直接删除
2,删除含有一个孩子的节点
我们不难看出,当我们删除一个节点的时候,我们直接把这个节点删除,然后把这个节点跟上就好了,十分的简单,如果你怕有风险,可以试试3或者13,我们试一下,你会发现这都是没有问题的
先连接当前节点的下一个节点,然后再把这个节点删除
3,删除有两个孩子的节点
我们可以看到这个有两种方法
方法一:
就是把15这个节点删除,然后在左子树寻找最大值放到删除的节点
方法二:
就是把15这个节点删除,然后再右子树寻找最小值放到删除的节点在左子树寻找最大值,在右子树寻找最大值
接下来我们就用代码来实现
BstNode* remove(BstNode* root, int data) {if (root == NULL) {return root;}else if (data < root->data) {root->left = remove(root->left, data);}else if (data < root->data) {root->right = remove(root->right, data);}else {//NO childrenif (root->left == NULL && root == NULL) {delete root;root = NULL;return root;}//One childrenelse if (root->left == NULL) {BstNode* temp = root;root = root->right;delete temp;return root;}else if (root->right == NULL) {BstNode* temp = root;root = root->left;delete temp;return root;}//two childrenelse {BstNode* temp = MAX(root->left);root->data = temp->data;root->left = remove(root->left, temp->data);}} }BstNode* MAX(BstNode* root) {if (root == NULL) {cout << "未找到" << endl;return NULL;}BstNode* current = root;while (current -> right != NULL) {current = current->right;}return current; }这个MAX就不用多说了,这个就是不断地到树的最右边进行查找,我们来看看这个删除的代码
第一部分
if (root == NULL) {return root; } else if (data < root->data) {root->left = remove(root->left, data); } else if (data < root->data) {root->right = remove(root->right, data); }这个是我们进行查找到这个值,直到我们找到那个值跳到else语句里面,这个为什么前面要有一个root->left/right进行接收呢?这个就是我们上一篇文章讨论的问题,我们需要不断地接受新的子树,不可以还是为原来地子树
第二部分
//NO children if (root->left == NULL && root == NULL) {delete root;root = NULL;return root; }这个是我直接删除叶子节点
第三部分
//One children else if (root->left == NULL) {BstNode* temp = root;root = root->right;delete temp;return root; } else if (root->right == NULL) {BstNode* temp = root;root = root->left;delete temp;return root; }这个是我们需要进行左右子树的删除我们root节点,这个节点我们用一个指针指着,然后把这个root节点改掉,改成指向root->right,然后返回这个root删除temp,左右子树都是一样的
第四部分
//two children else {BstNode* temp = MAX(root->left);root->data = temp->data;root->left = remove(root->left, temp->data); }这个就是我们把这个最大值找打,然后赋予给这个删除的地方,接下来我们就要找到这个节点并且删除,当我们找到之后,我们就又可以判断这个节点是哪一种,如果为两个孩子还要进行递归,如果为其他两种情况的话就是结束了
这个就是把两个孩子变成一个孩子或者没有孩子的情况
七,二叉收索树的中序后续节点
这个就是让你去判断你要使用中序的方法读取的那个节点的后面那个节点是多少,这个读者可以自行思考,后续也会更新这个代码的实现方法,这个就是让你用中序方法,假设为7,让你判断7后面那个几点为多少
总结
1,二叉搜索树的高度的计算
就是利用递归找到树的最低端头,先进行左子树的进行判断,然后在进行右子树的判断
2,广度优先VS深度优先
这两个就是,广度优先就是利用队列的方法把对应的推入到队列里面,然后再进行cout,然后利用pop弹出
3,判断是否为二叉搜索树
这个就是利用二叉树的性质,找到最大值和最小值,然后进行判断,运用递归,注意判断每个子树的时候要修改最值
4,删除节点
这个就是有三个方法,无孩子,1个孩子,2个孩子,2个孩子就是寻找最值然后再降为1个孩子或者没有孩子的情况
相关文章:

数据结构 树2
文章目录 前言 一,二叉搜索树的高度 二,广度优先VS深度优先 三,广度优先的代码实现 四,深度优先代码实现 五,判断是否为二叉搜索树 六,删除一个节点 七,二叉收索树的中序后续节点 总结 …...

GB/T 44721-2024 与 L3 自动驾驶:自动驾驶新时代的基石与指引
1.前言 在智能网联汽车飞速发展的当下,自动驾驶技术成为了行业变革的核心驱动力。从最初的辅助驾驶功能,到如今不断迈向高度自动化的征程,每一步都凝聚着技术的创新与突破。而在这一进程中,标准的制定与完善对于自动驾驶技术的规…...

AURIX TC275学习笔记3 官方例程 (UART LED WDT)
文章目录 参考资料1. ASCLIN_UART_12. GPIO_LED_Button_13. WDT (Watch Dog Timer) 参考资料 AURIX TC275学习笔记1 资料收集Getting Started with AURIX™ Development Studio 官方帮助文档happy hacking for TC275! 硬件平台使用AURIX™ TC275 Lite 套件,按照参…...

Vim的基础命令
移动光标 H(左) J(上) K(下) L(右) $ 表示移动到光标所在行的行尾, ^ 表示移动到光标所在行的行首的第一个非空白字符。 0 表示移动到光标所在行的行首。 W 光标向前跳转一个单词 w光标向前跳转一个单词 B光标向后跳转一个单词 b光标向后跳转一个单词 G 移动光标到…...

Linux的简单使用和部署4asszaaa0
一.部署 1 环境搭建方式主要有四种: 1. 直接安装在物理机上.但是Linux桌面使用起来非常不友好.所以不建议.[不推荐]. 2. 使用虚拟机软件,将Linux搭建在虚拟机上.但是由于当前的虚拟机软件(如VMWare之类的)存在⼀些bug,会导致环境上出现各种莫名其妙的问题比较折腾.[非常不推荐…...

Linux 的 sysfs 伪文件系统介绍【用户可以通过文件操作与内核交互(如调用内核函数),而无需编写内核代码】
1. 什么是 sysfs伪文件系统? sysfs 是 Linux 内核提供的 伪文件系统,用于向用户空间暴露内核对象的信息和控制接口。它是 procfs 的补充,主要用于管理 设备、驱动、内核子系统 等信息,使用户可以通过文件操作(如用户空…...

每日一题洛谷P5721 【深基4.例6】数字直角三角形c++
#include<iostream> using namespace std; int main() {int n;cin >> n;int t 1;for (int i 0; i < n; i) {for (int j 0; j < n - i; j) {printf("%02d",t);t;}cout << endl;}return 0; }...

计算机网络笔记再战——理解几个经典的协议1
目录 前言 从协议是什么出发 关于TCP/IP协议体系 几个传输方式的分类 地址 网卡 中继器(Repeater) 网桥(Bridge) 路由器(Router) 网关 前言 笔者最近正在整理(笔者开的坑不少…...

ElasticSearch学习笔记-解析JSON格式的内容
如果需要屏蔽其他项目对Elasticsearch的直接访问操作,统一由一个入口访问操作Elasticsearch,可以考虑直接传入JSON格式语句解析执行。 相关依赖包 <properties><elasticsearch.version>7.9.3</elasticsearch.version><elasticsea…...
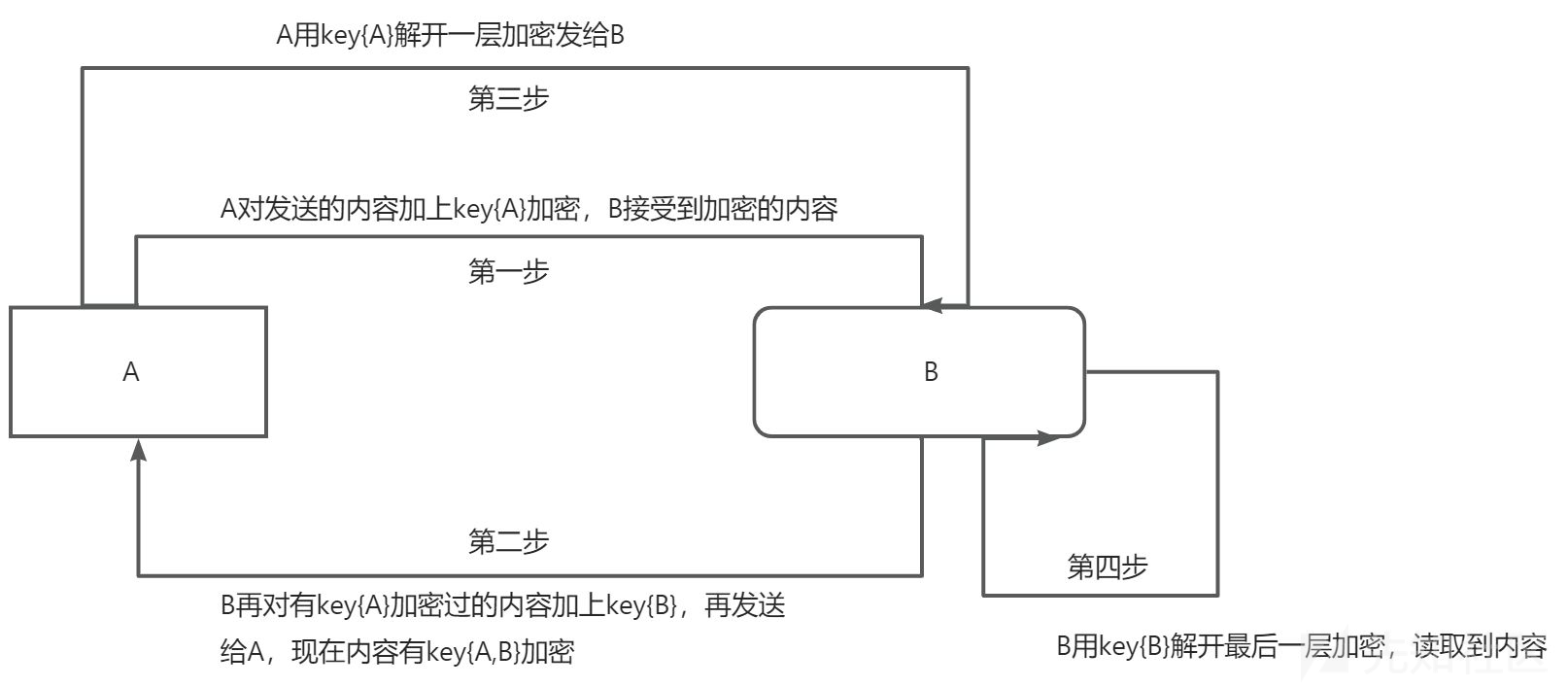
浅谈密码相关原理及代码实现
本代码仅供学习、研究、教育或合法用途。开发者明确声明其无意将该代码用于任何违法、犯罪或违反道德规范的行为。任何个人或组织在使用本代码时,需自行确保其行为符合所在国家或地区的法律法规。 开发者对任何因直接或间接使用该代码而导致的法律责任、经济损失或…...
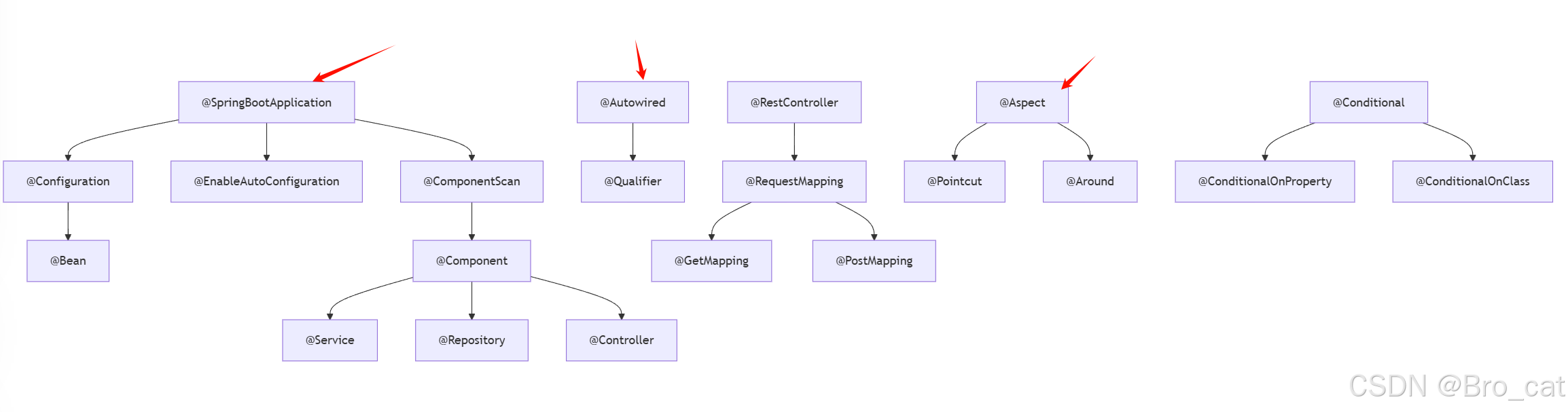
Spring Boot常用注解深度解析:从入门到精通
今天,这篇文章带你将深入理解Spring Boot中30常用注解,通过代码示例和关系图,帮助你彻底掌握Spring核心注解的使用场景和内在联系。 一、启动类与核心注解 1.1 SpringBootApplication 组合注解: SpringBootApplication Confi…...
can not add outlook new accounts on the outlook
link : Reference url...
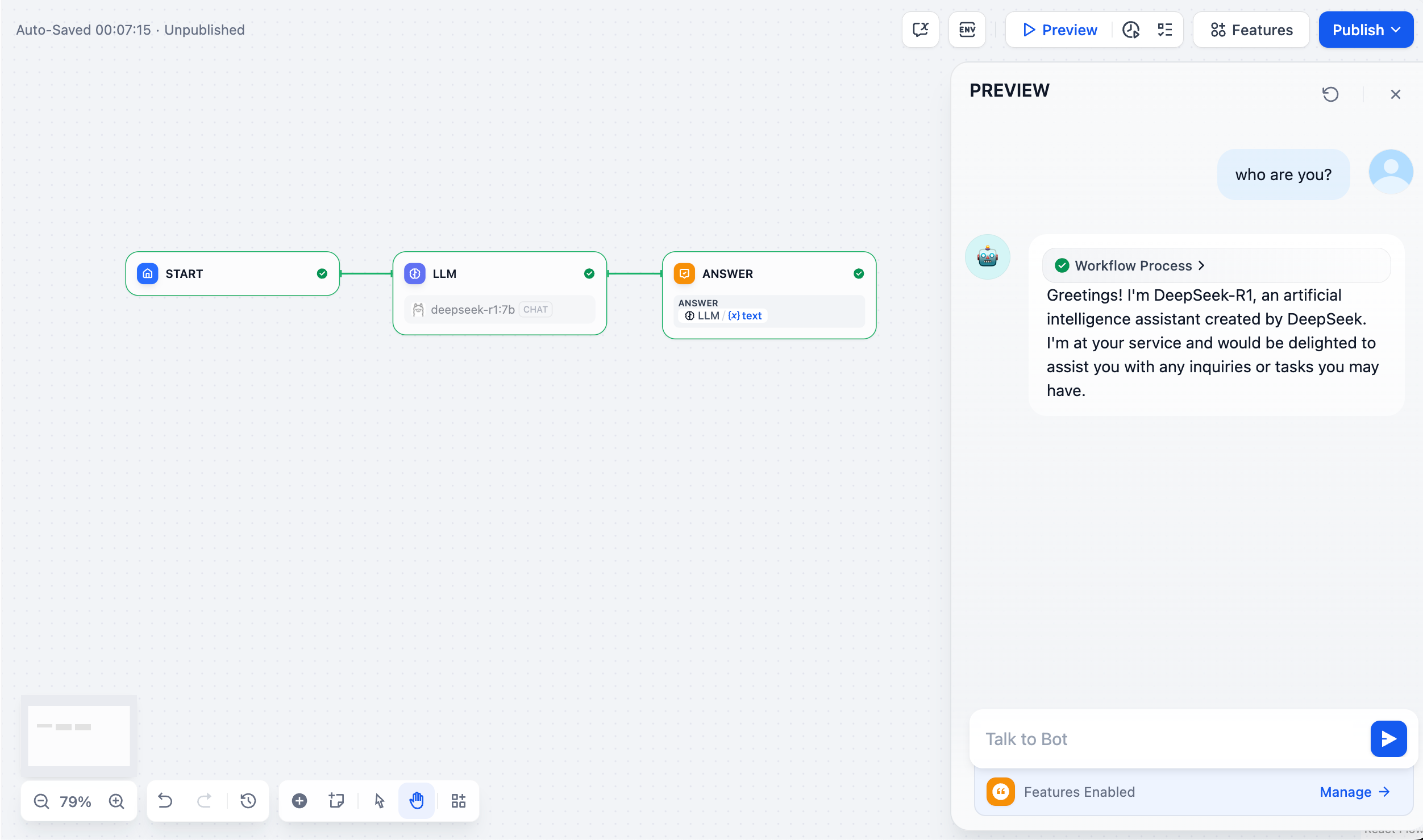
私有化部署 DeepSeek + Dify,构建你的专属私人 AI 助手
私有化部署 DeepSeek Dify,构建你的专属私人 AI 助手 概述 DeepSeek 是一款开创性的开源大语言模型,凭借其先进的算法架构和反思链能力,为 AI 对话交互带来了革新性的体验。通过私有化部署,你可以充分掌控数据安全和使用安全。…...

【Elasticsearch】post_filter
post_filter是 Elasticsearch 中的一种后置过滤机制,用于在查询执行完成后对结果进行过滤。以下是关于post_filter的详细介绍: 工作原理 • 查询后过滤:post_filter在查询执行完毕后对返回的文档集进行过滤。这意味着所有与查询匹配的文档都…...

验证工具:GVIM和VIM
一、定义与关系 gVim:gVim是Vim的图形界面版本,提供了更多的图形化功能,如菜单栏、工具栏和鼠标支持。它使得Vim的使用更加直观和方便,尤其对于不习惯命令行界面的用户来说。Vim:Vim是一个在命令行界面下运行的文本编…...
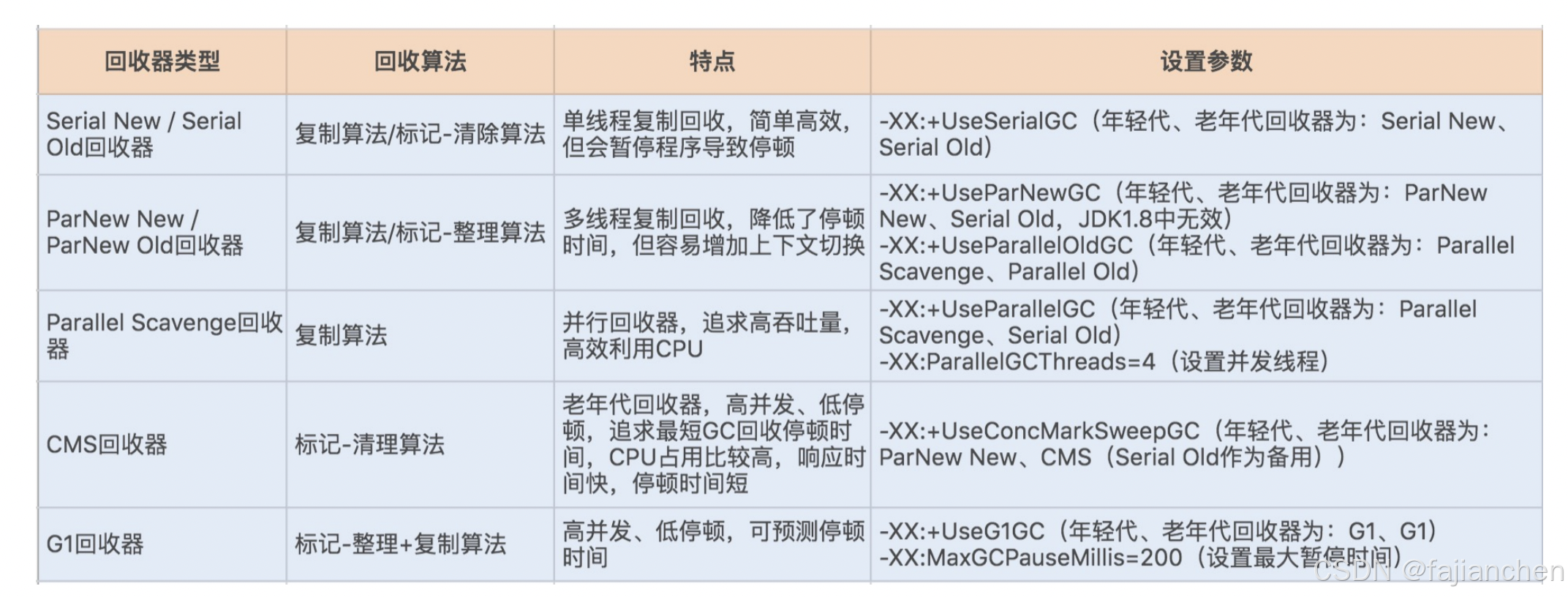
如何优化垃圾回收机制?
垃圾回收机制 掌握 GC 算法之前,我们需要先弄清楚 3 个问题。第一,回收发生在哪里?第二,对象在 什么时候可以被回收?第三,如何回收这些对象? 回收发生在哪里? JVM 的内存区域中&…...

beyond the ‘PHYSICAL‘ memory limit.问题处理
Container [pid5616,containerIDcontainer_e50_1734408743176_3027740_01_000006] is running 507887616B beyond the ‘PHYSICAL’ memory limit. Current usage: 4.5 GB of 4 GB physical memory used; 6.6 GB of 8.4 GB virtual memory used. Killing container. 1.增大map…...

Day36【AI思考】-表达式知识体系总览
文章目录 **表达式知识体系总览**回答1:**表达式知识体系****一、三种表达式形式对比****二、表达式转换核心方法****1. 中缀转后缀(重点)****2. 中缀转前缀** **三、表达式计算方法****1. 后缀表达式计算(栈实现)****…...
调试)
段错误(Segmentation Fault)调试
1. 使用 GDB(GNU Debugger) GDB 是一个强大的调试工具,可以帮助你逐步执行程序并检查变量状态。 编译时添加调试信息: gcc -g your_program.c -o your_program启动 GDB: gdb ./your_program运行程序: …...
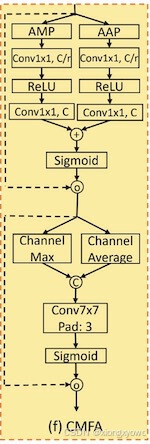
每日Attention学习19——Convolutional Multi-Focal Attention
每日Attention学习19——Convolutional Multi-Focal Attention 模块出处 [ICLR 25 Submission] [link] UltraLightUNet: Rethinking U-shaped Network with Multi-kernel Lightweight Convolutions for Medical Image Segmentation 模块名称 Convolutional Multi-Focal Atte…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

渗透实战PortSwigger靶场:lab13存储型DOM XSS详解
进来是需要留言的,先用做简单的 html 标签测试 发现面的</h1>不见了 数据包中找到了一个loadCommentsWithVulnerableEscapeHtml.js 他是把用户输入的<>进行 html 编码,输入的<>当成字符串处理回显到页面中,看来只是把用户输…...

Ubuntu系统多网卡多相机IP设置方法
目录 1、硬件情况 2、如何设置网卡和相机IP 2.1 万兆网卡连接交换机,交换机再连相机 2.1.1 网卡设置 2.1.2 相机设置 2.3 万兆网卡直连相机 1、硬件情况 2个网卡n个相机 电脑系统信息,系统版本:Ubuntu22.04.5 LTS;内核版本…...

Python实现简单音频数据压缩与解压算法
Python实现简单音频数据压缩与解压算法 引言 在音频数据处理中,压缩算法是降低存储成本和传输效率的关键技术。Python作为一门灵活且功能强大的编程语言,提供了丰富的库和工具来实现音频数据的压缩与解压。本文将通过一个简单的音频数据压缩与解压算法…...

热烈祝贺埃文科技正式加入可信数据空间发展联盟
2025年4月29日,在福州举办的第八届数字中国建设峰会“可信数据空间分论坛”上,可信数据空间发展联盟正式宣告成立。国家数据局党组书记、局长刘烈宏出席并致辞,强调该联盟是推进全国一体化数据市场建设的关键抓手。 郑州埃文科技有限公司&am…...





