【蓝桥】动态规划-简单-破损的楼梯
题目

解题思路
 完整代码
完整代码
#include <bits/stdc++.h>
using namespace std;
const int N=1e5+9;
const long long p=1e9+7;
long long dp[N];//dp[i]表示走到第i级台阶的方案数
bool broken[N];//broken代表破损台阶的数组
int main()
{int n,m;cin>>n>>m;for(int i=1;i<=m;i++){int x;cin>>x;broken[x]=true;//如果第x级台阶破损了,那就设置成true}dp[0]=1;//第1级台阶比较特殊,因为它只有一种走法,就是从第0级迈到第1级,所以单独列出if(!broken[1])//如果第一级台阶没有破损{dp[1]=1;}
//破损默认dp[1]为0for(int i=2;i<=n;i++)//如果第1级台阶坏了,那就从第2级台阶开始{if(broken[i]){continue;}dp[i]=(dp[i-1]+dp[i-2])%p;//因为一次可以迈1—2个台阶(即可以从i-1或i-2级迈到第i级),所以第i级的方案数等于i-2级的方案数 + i-1级的方案数}cout<<dp[n]<<endl;return 0;
}内存图助解
初始状态
在读取输入之前,flag 和 dp 数组都被初始化为 0,n 和 m 未赋值。
n: 未初始化
m: 未初始化flag: [0, 0, 0, 0, 0, 0, 0] // flag[0] 到 flag[6]
dp: [0, 0, 0, 0, 0, 0, 0] // dp[0] 到 dp[6]读取输入后的状态
读取 n = 6 和 m = 1 后,标记破损点 3。
n: 6
m: 1flag: [0, 0, 0, 1, 0, 0, 0] // flag[3] 被标记为 1
dp: [0, 0, 0, 0, 0, 0, 0] // dp 数组未初始化n: 6
m: 1flag: [0, 0, 0, 1, 0, 0, 0]
dp: [1, 0, 0, 0, 0, 0, 0] // dp[0] = 1,因为起点不是破损点第一步:计算 dp[1]
-
flag[1] = 0,不是破损点。 -
dp[1] = dp[0] = 1
n: 6
m: 1flag: [0, 0, 0, 1, 0, 0, 0]
dp: [1, 1, 0, 0, 0, 0, 0]第二步:计算 dp[2]
-
flag[2] = 0,不是破损点。 -
dp[2] = dp[1] + dp[0] = 1 + 1 = 2
n: 6
m: 1flag: [0, 0, 0, 1, 0, 0, 0]
dp: [1, 1, 2, 0, 0, 0, 0]第三步:计算 dp[3]
-
flag[3] = 1,是破损点,跳过。 -
dp[3] = 0
n: 6
m: 1flag: [0, 0, 0, 1, 0, 0, 0]
dp: [1, 1, 2, 0, 0, 0, 0]最终结果为
n: 6
m: 1flag: [0, 0, 0, 1, 0, 0, 0]
dp: [1, 1, 2, 0, 2, 2, 4]输出 dp[6],即到达终点的合法走法数量4
相关文章:

【蓝桥】动态规划-简单-破损的楼梯
题目 解题思路 完整代码 #include <bits/stdc.h> using namespace std; const int N1e59; const long long p1e97; long long dp[N];//dp[i]表示走到第i级台阶的方案数 bool broken[N];//broken代表破损台阶的数组 int main() {int n,m;cin>>n>>m;for(int …...

如何自定义软件安装路径及Scoop包管理器使用全攻略
如何自定义软件安装路径及Scoop包管理器使用全攻略 一、为什么无法通过WingetUI自定义安装路径? 问题背景: WingetUI是Windows包管理器Winget的图形化工具,但无法直接修改软件的默认安装路径。原因如下: Winget设计限制…...

107,【7】buuctf web [CISCN2019 华北赛区 Day2 Web1]Hack World
这次先不进入靶场 看到红框里面的话就想先看看uuid是啥 定义与概念 UUID 是 Universally Unique Identifier 的缩写,即通用唯一识别码。它是一种由数字和字母组成的 128 位标识符,在理论上可以保证在全球范围内的唯一性。UUID 的设计目的是让分布式系…...

STM32 ADC单通道配置
硬件电路 接线图: ADC基本结构图 代码配置 根据基本结构框图 1.定义结构体变量 //定义结构体变量 GPIO_InitTypeDef GPIO_InitStructure;//定义GPIO结构体变量 ADC_InitTypeDef ADC_InitStructure; //定义ADC结构体变量 2.开启RCC时钟 ADC、GPIO的时钟&#x…...

【技海登峰】Kafka漫谈系列(二)Kafka高可用副本的数据同步与选主机制
【技海登峰】Kafka漫谈系列(二)Kafka高可用副本的数据同步与选主机制 一. 数据同步 在之前的学习中有了副本Replica的概念,解决了数据备份的问题。我们还需要面临一个设计难题即:如何处理分区中Leader与Follwer节点数据同步不匹配问题所带来的风险,这也是保证数据高可用的…...

Spring的三级缓存如何解决循环依赖问题
循环依赖问题是在对象之间存在相互依赖关系,形成一个闭环,导致无法准确的完成对象的创建和初始化,当两个或多个对象彼此之间相互引用,这种相互引用形成一个循环时,就可能出现循环依赖问题。 在 Spring 框架中…...

Ext文件系统
文件内容属性 被打开的文件在内存中,没有被打开的文件在磁盘里文件系统的工作就是根据路径帮我们找到在磁盘上的文件 磁盘(硬件) 磁盘的存储结构 磁头在传动臂的运动下共同进退,向磁盘写入的时候是向柱面批量写入的 OS文件系统访…...

回溯算法---数独问题
回溯算法理论基础 回溯和递归密不可分,有回溯就有递归,所谓回溯就是基于一个叉树,可能是二叉树或者是三叉树,从root节点开始深度优先搜索遍历节点,当遍历到一个子节点时,回溯到上一个根节点选择另外一个子…...
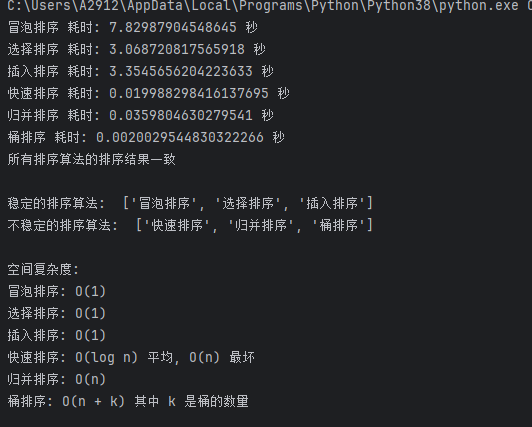
蓝桥杯python基础算法(2-1)——排序
目录 一、排序 二、例题 P3225——宝藏排序Ⅰ 三、各种排序比较 四、例题 P3226——宝藏排序Ⅱ 一、排序 (一)冒泡排序 基本思想:比较相邻的元素,如果顺序错误就把它们交换过来。 (二)选择排序 基本思想…...

【课程笔记】信息隐藏与数字水印
文章总览:YuanDaiMa2048博客文章总览 【课程笔记】信息隐藏与数字水印 信号处理基础知识隐写系统隐写算法性能指标音频信号处理基础数字音频概念人类听觉系统与语音质量评价信息隐藏的原理数字指纹与版权保护盲水印与非盲水印私钥水印与公钥水印信息隐藏的研究层次信息隐藏与数…...

Page Assist实现deepseek离线部署的在线搜索功能
前面文章Mac 基于Ollama 本地部署DeepSeek离线模型 实现了deepseek的离线部署,但是部署完成虽然可以进行问答和交互,也有thinking过程,但是没办法像官方一样进行联网搜索。今天我们介绍一款浏览器插件Page Assist来实现联网搜索,完…...

composeUI中Box 和 Surface的区别
在 Jetpack Compose 中,Box 和 Surface 都是常用的布局组件,但它们的用途和功能有所不同。 Box 组件: 功能:Box 是一个用于将子组件堆叠在一起的布局容器,类似于传统 Android 中的 FrameLayout。用途:适用…...

【LeetCode】5. 贪心算法:买卖股票时机
太久没更了,抽空学习下。 看一道简单题。 class Solution:def maxProfit(self, prices: List[int]) -> int:cost -1profit 0for i in prices:if cost -1:cost icontinueprofit_ i - costif profit_ > profit:profit profit_if cost > i:cost iret…...

MySQL表的CURD
目录 一、Create 1.1单行数据全列插入 1.2多行数据指定列插入 1.3插入否则更新 1.4替换 2.Retrieve 2.1 select列 2.1.1全列查询 2.1.2指定列查询 2.1.3查询字段为表达式 2.1.4为查询结果指定别名 2.1.5结果去重 2.2where条件 2.3结果排序 2.4筛选分页结果 三…...

Java 如何覆盖第三方 jar 包中的类
目录 一、需求描述二、示例描述三、操作步骤四、验证结果五、实现原理 背景: 在我们日常的开发中,经常需要使用第三方的 jar 包,有时候我们会发现第三方的 jar 包中的某一个类有问题,或者我们需要定制化修改其中的逻辑,…...

VSCode中使用EmmyLua插件对Unity的tolua断点调试
一.VSCode中搜索安装EmmyLua插件 二.创建和编辑launch.json文件 初始的launch.json是这样的 手动编辑加上一段内容如下图所示: 三.启动调试模式,并选择附加的进程...
【数据结构】_链表经典算法OJ(力扣/牛客第二弹)
目录 1. 题目1:返回倒数第k个节点 1.1 题目链接及描述 1.2 解题思路 1.3 程序 2. 题目2:链表的回文结构 2.1 题目链接及描述 2.2 解题思路 2.3 程序 1. 题目1:返回倒数第k个节点 1.1 题目链接及描述 题目链接: 面试题 …...

Spring Boot 2 快速教程:WebFlux优缺点及性能分析(四)
WebFlux优缺点 【来源DeepSeek】 Spring WebFlux 是 Spring 框架提供的响应式编程模型,旨在支持非阻塞、异步和高并发的应用场景。其优缺点如下: 优点 高并发与低资源消耗 非阻塞 I/O:基于事件循环模型(如 Netty)&am…...

自定义多功能输入对话框:基于 Qt 打造灵活交互界面
一、引言 在使用 Qt 进行应用程序开发时,我们经常需要与用户进行交互,获取他们输入的各种信息。QInputDialog 是 Qt 提供的一个便捷工具,可用于简单的输入场景,但当需求变得复杂,需要支持更多类型的输入控件࿰…...

基于springboot河南省旅游管理系统
基于Spring Boot的河南省旅游管理系统是一种专为河南省旅游行业设计的信息管理系统,旨在整合和管理河南省的旅游资源信息,为游客提供准确、全面的旅游攻略和服务。以下是对该系统的详细介绍: 一、系统背景与意义 河南省作为中国的中部省份&…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...

【Kafka】Kafka从入门到实战:构建高吞吐量分布式消息系统
Kafka从入门到实战:构建高吞吐量分布式消息系统 一、Kafka概述 Apache Kafka是一个分布式流处理平台,最初由LinkedIn开发,后成为Apache顶级项目。它被设计用于高吞吐量、低延迟的消息处理,能够处理来自多个生产者的海量数据,并将这些数据实时传递给消费者。 Kafka核心特…...

PH热榜 | 2025-06-08
1. Thiings 标语:一套超过1900个免费AI生成的3D图标集合 介绍:Thiings是一个不断扩展的免费AI生成3D图标库,目前已有超过1900个图标。你可以按照主题浏览,生成自己的图标,或者下载整个图标集。所有图标都可以在个人或…...
