LeetCode 0063.不同路径 II:动态规划 - 原地使用地图数组,几乎无额外空间开销
【LetMeFly】63.不同路径 II:动态规划 - 原地使用地图数组,几乎无额外空间开销
力扣题目链接:https://leetcode.cn/problems/unique-paths-ii/
给定一个 m x n 的整数数组 grid。一个机器人初始位于 左上角(即 grid[0][0])。机器人尝试移动到 右下角(即 grid[m - 1][n - 1])。机器人每次只能向下或者向右移动一步。
网格中的障碍物和空位置分别用 1 和 0 来表示。机器人的移动路径中不能包含 任何 有障碍物的方格。
返回机器人能够到达右下角的不同路径数量。
测试用例保证答案小于等于 2 * 109。
示例 1:

输入:obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出:2
解释:3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径:
1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右
示例 2:

输入:obstacleGrid = [[0,1],[0,0]] 输出:1
提示:
m == obstacleGrid.lengthn == obstacleGrid[i].length1 <= m, n <= 100obstacleGrid[i][j]为0或1
解题方法:动态规划
直接使用原来的obstacleGrid数组,令obstacleGrid[i][j]代表走到(i, j)为止的总方案数。
因为是原地修改,所以就要求我们从左到右从上到下按顺序遍历。
遍历到一个元素时:
- 如果这个元素为
1,就说明这里是障碍,走这里的方案数为0; - 否则,走这里的方案数为“由上面来”和“由左边来”的方案数之和(若不可由上而来则将“由上面来”的方案数记为1)。
特别的,对于起始位置obstacleGrid[0][0]:
- 若初始值为
1说明不可从这里出发,总方案数为0; - 若初始值为
0说明可以从这里出发,令obstacleGrid[0][0] = 1。
时空复杂度分析
- 时间复杂度 O ( s i z e ( o b s t a c l e G r i d ) ) O(size(obstacleGrid)) O(size(obstacleGrid))
- 空间复杂度 O ( 1 ) O(1) O(1)
AC代码
Python
'''
Author: LetMeFly
Date: 2025-02-08 09:55:16
LastEditors: LetMeFly.xyz
LastEditTime: 2025-02-08 09:58:42
'''
from typing import Listclass Solution:def uniquePathsWithObstacles(self, a: List[List[int]]) -> int:a[0][0] = 0 if a[0][0] else 1for i in range(len(a)):for j in range(len(a[0])):if a[i][j] != 0 and (i or j):a[i][j] = 0continueif i > 0:a[i][j] += a[i - 1][j]if j > 0:a[i][j] += a[i][j - 1]return a[-1][-1]
C++
/** @Author: LetMeFly* @Date: 2025-02-08 09:36:16* @LastEditors: LetMeFly.xyz* @LastEditTime: 2025-02-08 09:53:50*/
class Solution {
public:int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {for (int i = 0; i < obstacleGrid.size(); i++) {for (int j = 0; j < obstacleGrid[0].size(); j++) {if (i == 0 && j == 0) {obstacleGrid[i][j] = obstacleGrid[i][j] ? 0 : 1;continue;} else if (obstacleGrid[i][j]) {obstacleGrid[i][j] = -1;continue;}if (i > 0 && obstacleGrid[i - 1][j] != -1) {obstacleGrid[i][j] += obstacleGrid[i - 1][j];}if (j > 0 && obstacleGrid[i][j - 1] != -1) {obstacleGrid[i][j] += obstacleGrid[i][j - 1];}}}return max(obstacleGrid.back().back(), 0);}
};
Java
/** @Author: LetMeFly* @Date: 2025-02-08 09:55:20* @LastEditors: LetMeFly.xyz* @LastEditTime: 2025-02-08 10:02:07*/
class Solution {public int uniquePathsWithObstacles(int[][] a) {if (a[0][0] == 1) {return 0;}a[0][0] = 1;for (int i = 0; i < a.length; i++) {for (int j = 0; j < a[0].length; j++) {if (a[i][j] == 1 && i + j > 0) {a[i][j] = 0;continue;}if (i > 0) {a[i][j] += a[i - 1][j];}if (j > 0) {a[i][j] += a[i][j - 1];}}}return a[a.length - 1][a[0].length - 1];}
}
Go
/** @Author: LetMeFly* @Date: 2025-02-08 09:55:29* @LastEditors: LetMeFly.xyz* @LastEditTime: 2025-02-08 10:04:49*/
package mainfunc uniquePathsWithObstacles(a [][]int) int {if a[0][0] == 1 {return 0}a[0][0] = 1for i := range a {for j := range a[0] {if a[i][j] == 1 && i + j > 0 {a[i][j] = 0continue}if i > 0 {a[i][j] += a[i - 1][j]}if j > 0 {a[i][j] += a[i][j - 1]}}}return a[len(a) - 1][len(a[0]) - 1]
}
同步发文于CSDN和我的个人博客,原创不易,转载经作者同意后请附上原文链接哦~
千篇源码题解已开源
Tisfy:https://letmefly.blog.csdn.net/article/details/145509662
相关文章:

LeetCode 0063.不同路径 II:动态规划 - 原地使用地图数组,几乎无额外空间开销
【LetMeFly】63.不同路径 II:动态规划 - 原地使用地图数组,几乎无额外空间开销 力扣题目链接:https://leetcode.cn/problems/unique-paths-ii/ 给定一个 m x n 的整数数组 grid。一个机器人初始位于 左上角(即 grid[0][0]&#…...

elementui:el-table支持搜索、切换分页多选功能,以及数据回显
1、el-table相关代码,需注意:row-key"(row) > { return row.id }" 以及 :reserve-selection"true" <div class"boxList"><div class"search-form"><!-- 搜索表单 --><el-form :inline"true&q…...

深度整理总结MySQL——索引正确使用姿势
索引正确使用姿势 前言MySQL索引优缺点分析✅ 索引的优势⚠️ 索引的代价 如何合理建立索引?——关键原则总结重要的优化机制索引覆盖——通俗的方式讲解索引下推索引跳跃式扫描 前言 这篇文章是补充一些基本概念和实战的一些使用建议. MySQL索引优缺点分析 ✅ 索引的优势 …...

使用LLaMA Factory踩坑记录
前置条件:电脑显卡RTX 4080 问题:LLaMA-Factory在运行的时候,弹出未检测到CUDA的报错信息 结论:出现了以上的报错,主要可以归结于以下两个方面: 1、没有安装GPU版本的pytorch,下载的是CPU版本…...

亚博microros小车-原生ubuntu支持系列:25 二维码控制运动
二维码识别 安装依赖 pip3 install pyzbarsudo apt install libzbar-dev 在用小车识别之前,先用电脑的摄像头测试下基本的识别 import cv2 import rclpy from rclpy.node import Node import pyzbar.pyzbar as pyzbar import numpy as np from ament_index_pyth…...
基于深度学习的人工智能量化衰老模型构建与全流程应用研究
一、引言 1.1 研究背景与意义 1.1.1 人口老龄化现状与挑战 人口老龄化是当今全球面临的重要社会趋势之一,其发展态势迅猛且影响深远。根据联合国的相关数据,1980 年,全球 65 岁及以上人口数量仅为 2.6 亿,到 2021 年,这一数字已翻番,达到 7.61 亿,而预计到 2050 年,…...

【医院运营统计专题】2.运营统计:医院管理的“智慧大脑”
医院成本核算、绩效管理、运营统计、内部控制、管理会计专题索引 引言 在当今医疗行业快速发展的背景下,医院运营管理的科学性和有效性成为了决定医院竞争力和可持续发展能力的关键因素。运营统计作为医院管理的重要工具,通过对医院各类数据的收集、整理、分析和解读,为医…...

Spring Boot Actuator使用
说明:本文介绍Spring Boot Actuator的使用,关于Spring Boot Actuator介绍,下面这篇博客写得很好,珠玉在前,我就不多介绍了。 Spring Boot Actuator 简单使用 项目里引入下面这个依赖 <!--Spring Boot Actuator依…...

【AI应用】免费的文本转语音工具:微软 Edge TTS 和 开源版 ChatTTS 对比
【AI论文解读】【AI知识点】【AI小项目】【AI战略思考】【AI日记】【读书与思考】【AI应用】 我试用了下Edge TTS,感觉还不错,不过它不支持克隆声音(比如自己的声音) 微软 Edge TTS 和 开源版 ChatTTS 都是免费的 文本转语音&…...
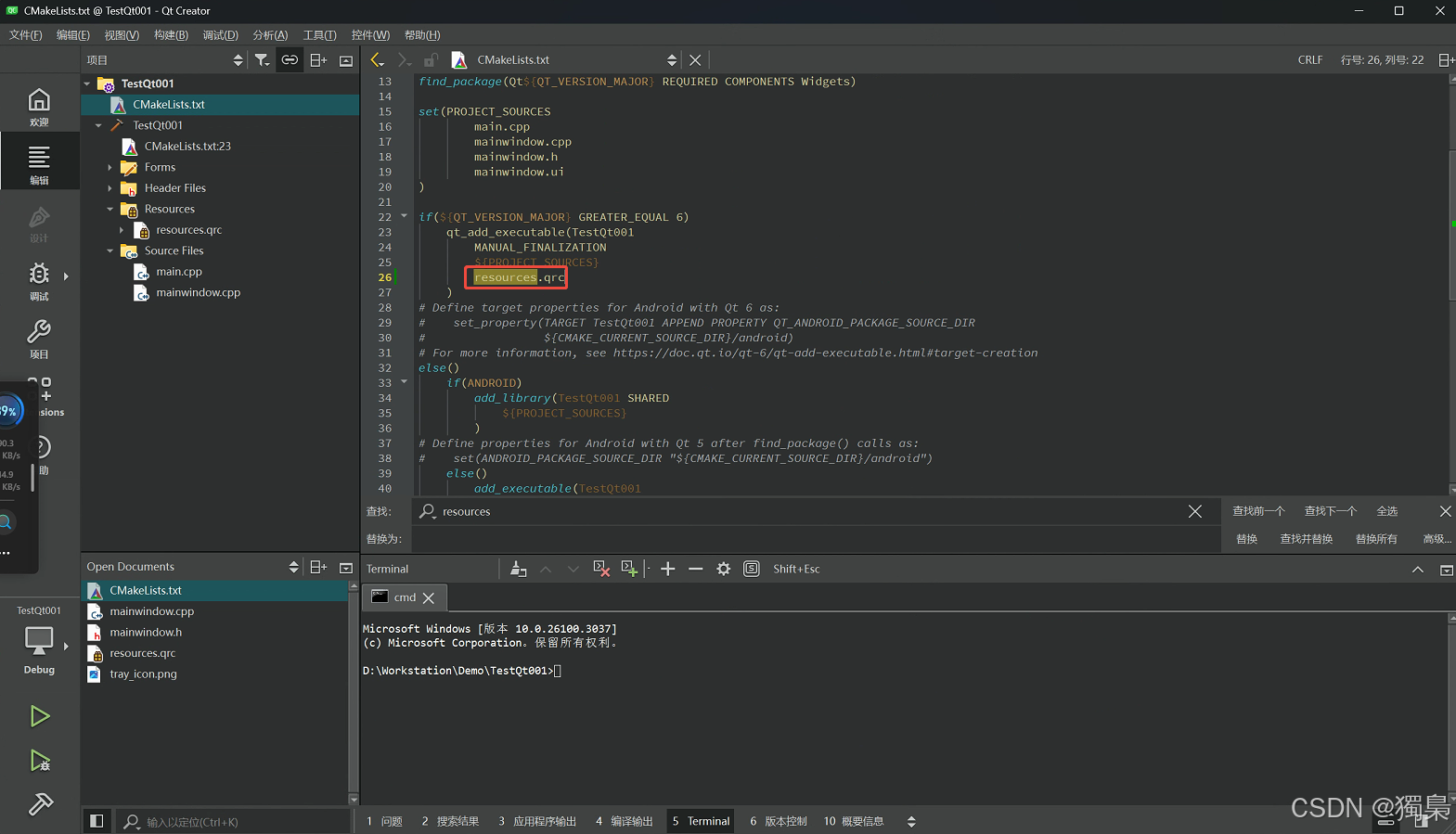
如何在 Qt 中添加和使用系统托盘图标
在 Qt 中实现系统托盘图标是一个常见的需求,尤其是在桌面应用程序中。系统托盘图标可以让应用程序在后台运行时仍然具有可见性,同时避免占用过多的桌面空间。本文将详细介绍如何在 Qt 项目中添加托盘图标,并通过资源系统(.qrc 文件…...
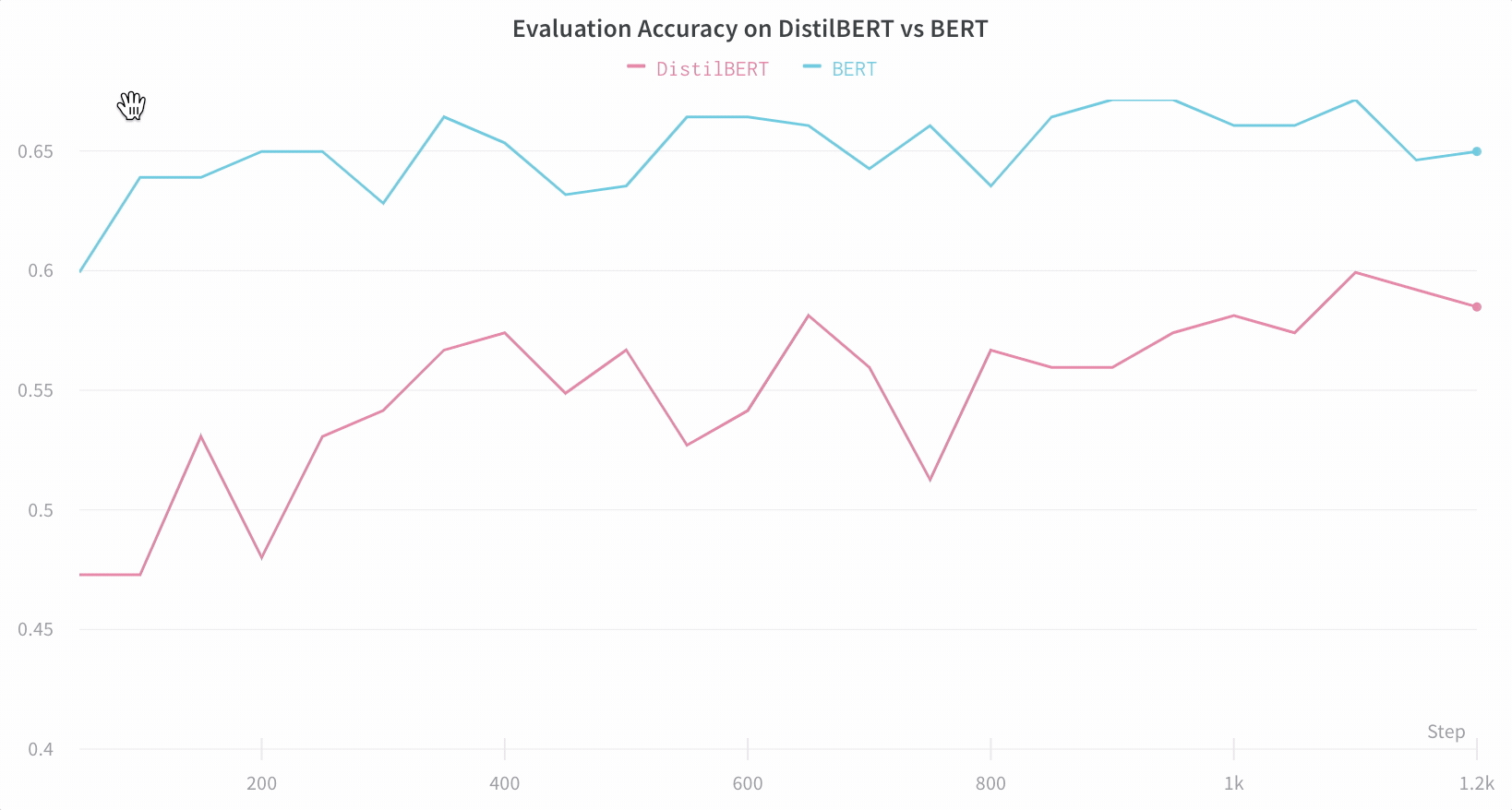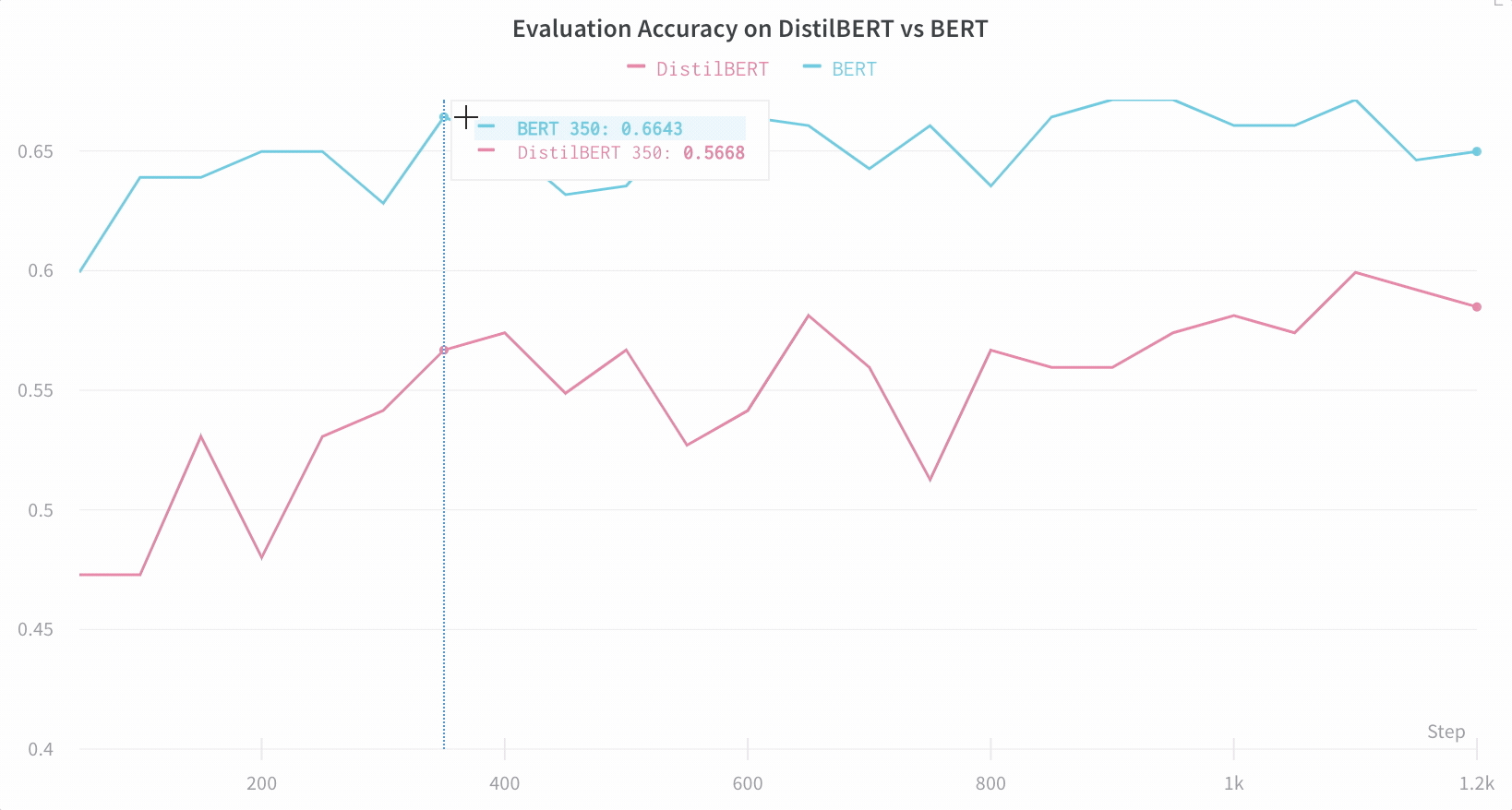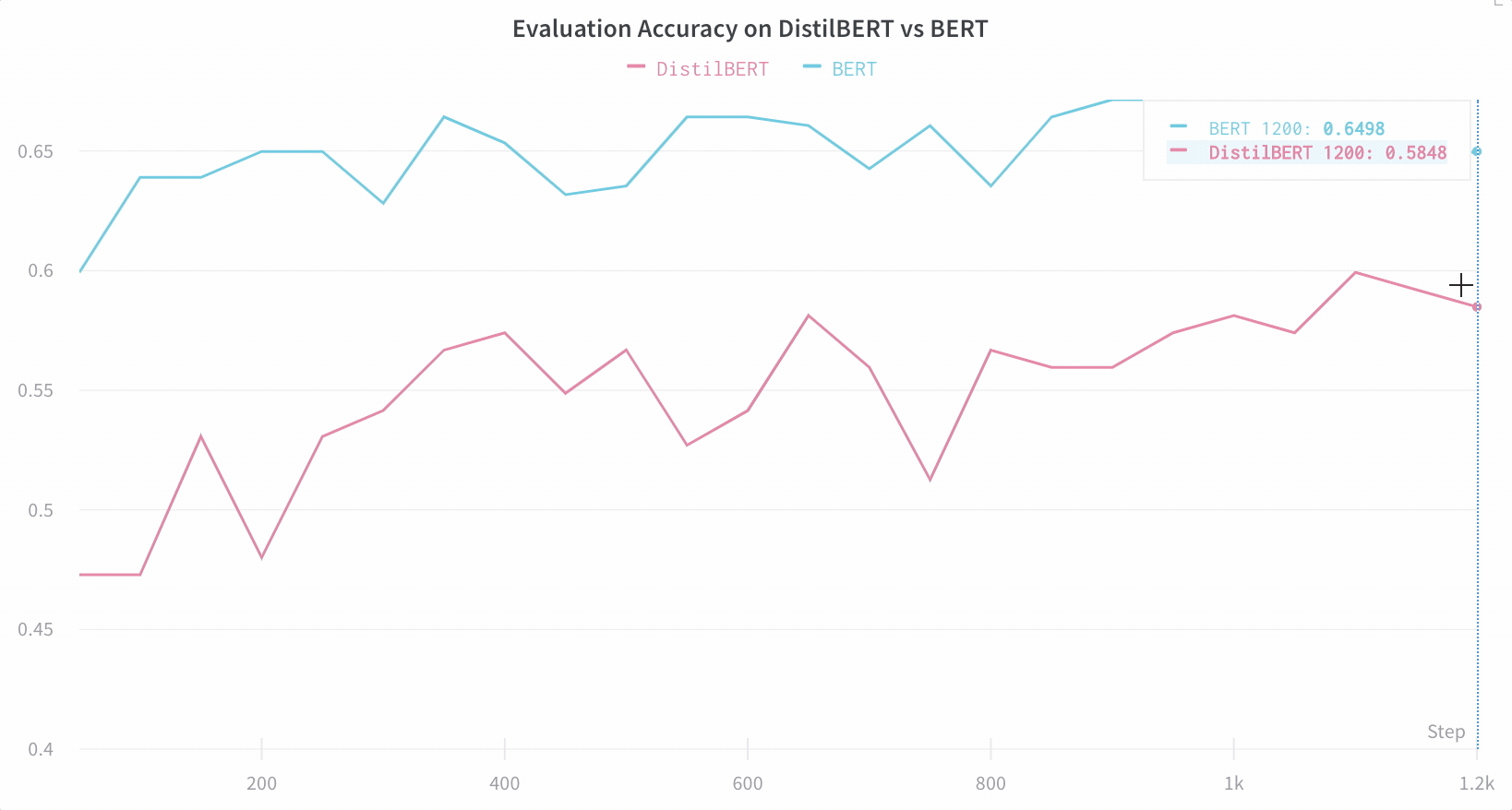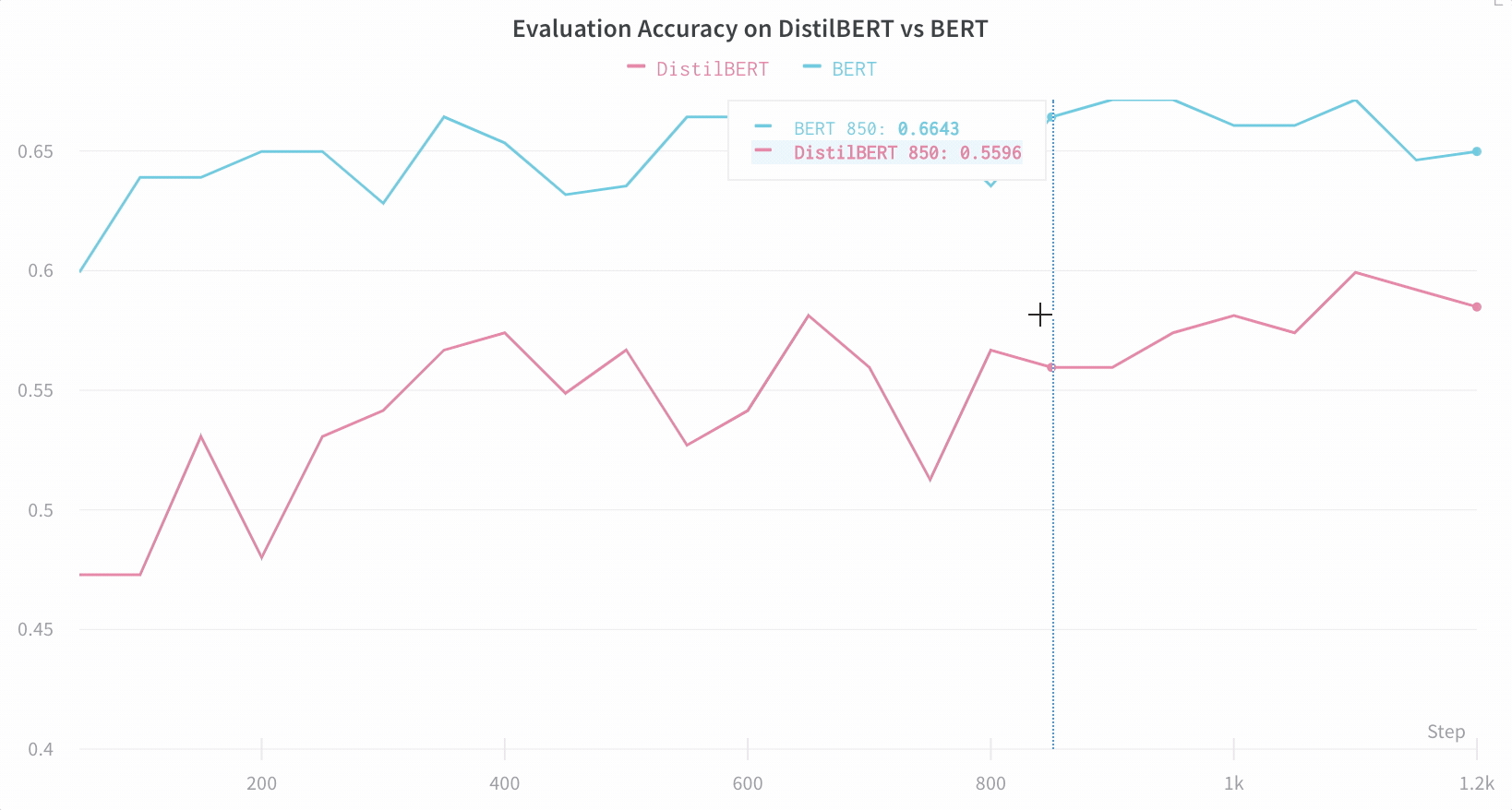
【WB 深度学习实验管理】利用 Hugging Face 实现高效的自然语言处理实验跟踪与可视化
本文使用到的 Jupyter Notebook 可在GitHub仓库002文件夹找到,别忘了给仓库点个小心心~~~ https://github.com/LFF8888/FF-Studio-Resources 在自然语言处理领域,使用Hugging Face的Transformers库进行模型训练已经成为主流。然而,随着模型复…...
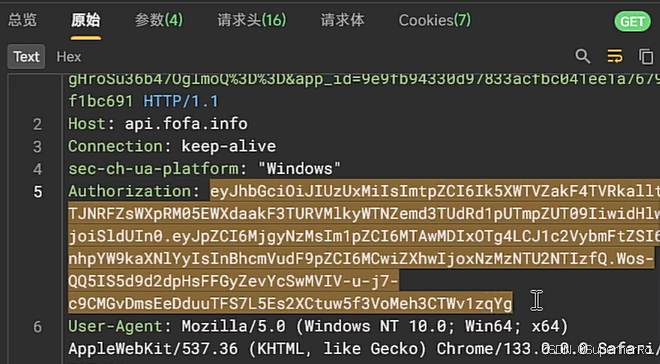
基础入门-网站协议身份鉴权OAuth2安全Token令牌JWT值Authirization标头
知识点: 1、网站协议-http/https安全差异(抓包) 2、身份鉴权-HTTP头&OAuth2&JWT&Token 一、演示案例-网站协议-http&https-安全测试差异性 1、加密方式 HTTP:使用明文传输,数据在传输过程中可以被…...
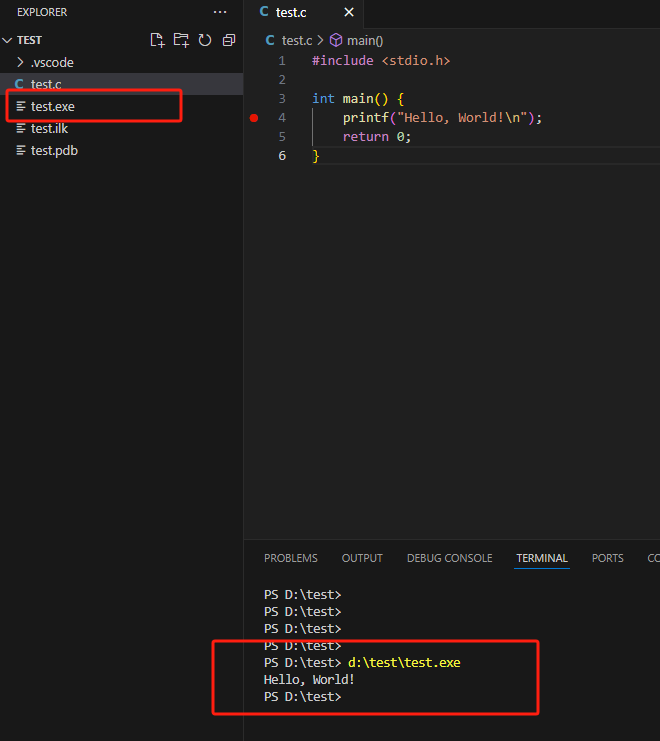
C语言基础系列【3】VSCode使用
前面我们提到过VSCode有多么的好用,本文主要介绍如何使用VSCode编译运行C语言代码。 安装 首先去官网(https://code.visualstudio.com/)下载安装包,点击Download for Windows 获取安装包后,一路点击Next就可以。 配…...

MySQL-5.7.44安装(CentOS7)
目录 1、下载安装包并解压 2、创建数据目录与日志目录 3、设置环境变量 4、刷新环境变量 5、执行初始化 6、创建配置文件目录 7、新建配置文件 8、为安装目录赋予可执行权限 9、创建服务启动脚本 10、启动服务并将启动脚本加入开机自启动 11、查看服务状态 12、创建…...

服务端与多客户端照片的传输,recv,send
一、照片传输 server.c /* * 文件名称:server.c * 创 建 者: * 创建日期:2025年02月07日 * 描 述: */ #include <stdio.h> #include <sys/types.h> /* See NOTES */ #include <sys/socket.h…...

JS实现灯光闪烁效果
在 JS中,我们可以实现灯光闪烁效果,这里主要用 setInterval 和 clearInterval 两个重要方法。 效果图 源代码 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>灯闪烁效果<…...

SpringCloud面试题----Nacos和Eureka的区别
功能特性 服务发现 Nacos:支持基于 DNS 和 RPC 的服务发现,提供了更为灵活的服务发现机制,能满足不同场景下的服务发现需求。Eureka:主要基于 HTTP 的 RESTful 接口进行服务发现,客户端通过向 Eureka Server 发送 HT…...

verilog练习:i2c slave 模块设计
文章目录 前言1. 结构2.代码2.1 iic_slave.v2.2 sync.v2.3 wr_fsm.v2.3.1 状态机状态解释 2.4 ram.v 3. 波形展示4. 建议5. 资料总结 前言 首先就不啰嗦iic协议了,网上有不少资料都是叙述此协议的。 下面将是我本次设计的一些局部设计汇总,如果对读者有…...
)
3.5 Go(特殊函数)
目录 一、匿名函数 1、匿名函数的特点: 2、匿名函数代码示例 2、匿名函数的类型 二、递归函数 1. 递推公式版本 2. 循环改递归 三、嵌套函数 1、嵌套函数用途 2、代码示例 3、作用域 & 变量生存周期 四、闭包 1、闭包使用场景 2、代码示例 五、De…...

Android的MQTT客户端实现
在 Android 平台上实现 MQTT 客户端的完整技术方案,涵盖基础实现、安全连接、性能优化和最佳实践: 一、技术选型与依赖配置 推荐库 Eclipse Paho Android Service(官方维护,支持后台运行) gradle 复制 // build.gradl…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...
