反函数定义及其推导
文章目录
- 定义
- 存在条件
- 举例说明
- 总结
反函数是数学中一种特殊的函数,用于“逆转”另一个函数的映射关系。
定义
设有一个函数 f : X → Y f: X \to Y f:X→Y。如果存在一个函数 g : Y → X g: Y \to X g:Y→X,使得对于所有 x ∈ X x \in X x∈X 和 y ∈ Y y \in Y y∈Y 都满足下面两个条件:
- 左逆性质: g ( f ( x ) ) = x g(f(x)) = x g(f(x))=x (对于所有 x ∈ X x \in X x∈X)
- 右逆性质: f ( g ( y ) ) = y f(g(y)) = y f(g(y))=y (对于所有 y ∈ Y y \in Y y∈Y)
那么函数 g g g 就称为函数 f f f 的反函数,记作 f − 1 f^{-1} f−1。
存在条件
反函数 f − 1 f^{-1} f−1 存在的充分必要条件是函数 f f f 必须是一个双射(即既单射又满射):
- 单射(一一对应):不同的 x x x 映射到不同的 y y y。
- 满射:函数 f f f 的值覆盖了整个 Y Y Y 集合。
如果 f f f 不是双射,那么反函数在严格意义上不存在。
举例说明
假设有函数 f ( x ) = 2 x + 3 f(x) = 2x + 3 f(x)=2x+3 ,它是双射(在实数集合上),那么可以求其反函数:
- 写出方程: y = 2 x + 3 y = 2x + 3 y=2x+3。
- 解这个方程得到 x x x: x = y − 3 2 x = \frac{y - 3}{2} x=2y−3。
- 因此, f − 1 ( y ) = y − 3 2 f^{-1}(y) = \frac{y - 3}{2} f−1(y)=2y−3 或记作 f − 1 ( x ) = x − 3 2 f^{-1}(x) = \frac{x - 3}{2} f−1(x)=2x−3。
验证:
- f ( f − 1 ( x ) ) = 2 ( x − 3 2 ) + 3 = x − 3 + 3 = x f(f^{-1}(x)) = 2\left(\frac{x - 3}{2}\right) + 3 = x - 3 + 3 = x f(f−1(x))=2(2x−3)+3=x−3+3=x。
- f − 1 ( f ( x ) ) = ( 2 x + 3 ) − 3 2 = x f^{-1}(f(x)) = \frac{(2x + 3) - 3}{2} = x f−1(f(x))=2(2x+3)−3=x。
这说明 f − 1 f^{-1} f−1 确实是 f f f 的反函数。
总结
反函数的核心思想是将函数的映射过程反过来。对于每个 y = f ( x ) y = f(x) y=f(x),反函数 f − 1 f^{-1} f−1 能够唯一地将 y y y 映射回 x x x。这在解决方程、数据逆变换、以及其他许多数学和工程问题中都有广泛应用。
ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ
ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ
相关文章:

反函数定义及其推导
文章目录 定义存在条件举例说明总结 反函数是数学中一种特殊的函数,用于“逆转”另一个函数的映射关系。 定义 设有一个函数 f : X → Y f: X \to Y f:X→Y。如果存在一个函数 g : Y → X g: Y \to X g:Y→X,使得对于所有 x ∈ X x \in X x∈X 和 y…...

2025.2.9机器学习笔记:PINN文献阅读
2025.2.9周报 文献阅读题目信息摘要Abstract创新点网络架构实验结论缺点以及后续展望 文献阅读 题目信息 题目: GPT-PINN:Generative Pre-Trained Physics-Informed Neural Networks toward non-intrusive Meta-learning of parametric PDEs期刊: Fini…...

Oracle数据连接 Dblink
拓展: oracle远程登陆数据库 1.oracle客户端或者服务端 2.修改你的电脑如下路径文件(服务器IP,服务器的数据库名,服务器的数据库端口号) c:\oracle\product\10.2.0\db_1\NETWORK\ADMIN\tnsnames.ora orcl_109 (DESCRIPTION …...

fetch请求总结,fastadmin中后台接口强制返回json数据
fetch请求 提交图片,只支持formData方式,这样会自动变为multiform方式,而且一般的post大多都可以用这样的方式来完成请求 const formData new FormData(); formData.append(file, fileInput.files[0]); formData.append(pid, id); formData.append(dc, 1);fetch(/api/common…...

基于STM32的智能鱼缸水质净化系统设计
🤞🤞大家好,这里是5132单片机毕设设计项目分享,今天给大家分享的是智能鱼缸水质净化系统。 目录 1、设计要求 2、系统功能 3、演示视频和实物 4、系统设计框图 5、软件设计流程图 6、原理图 7、主程序 8、总结 1、设计要求…...

JAVA安全—FastJson反序列化利用链跟踪autoType绕过
前言 FastJson这个漏洞我们之前讲过了,今天主要是对它的链条进行分析一下,明白链条的构造原理。 Java安全—log4j日志&FastJson序列化&JNDI注入_log4j漏洞-CSDN博客 漏洞版本 1.2.24及以下没有对序列化的类做校验,导致漏洞产生 1.2.25-1.2.41增加了黑名单限制,…...
)
格式化字符串漏洞(Format String Vulnerability)
格式化字符串漏洞(Format String Vulnerability)是程序中因不当处理格式化字符串参数而导致的一类安全漏洞,常被攻击者利用来读取内存数据、篡改程序执行流程,甚至执行任意代码。以下是对其原理、利用方式及防御措施的详细解析&am…...

C++--iomanip库
目录 1. 设置字段宽度:std::setw() 2. 设置浮点数精度:std::setprecision() 3. 设置填充字符:std::setfill() 4. 控制对齐方式:std::left 和 std::right,std::internal 5. 控制进制输出:std::hex、std…...

Redis 集群原理、主从复制和哨兵模式的详细讲解
引言:本文记录了博主在学习Redis的过程中的原理,了解为什么使用与怎么样使用 Redis 集群,在使用 Redis 集群时出现的主从复制和哨兵模式的相关知识。本文并不涉及Redis安装。 文章目录 一、简单介绍什么是 Redis二、为什么要使用 Redis 集群三…...

基于Java的远程视频会议系统(源码+系统+论文)
第一章 概述 1.1 本课题的研究背景 随着人们对视频和音频信息的需求愈来愈强烈,追求远距离的视音频的同步交互成为新的时尚。近些年来,依托计算机技术、通信技术和网络条件的发展,集音频、视频、图像、文字、数据为一体的多媒体信息ÿ…...

springboot 事务管理
在Spring Boot中,事务管理是通过Spring框架的事务管理模块来实现的。Spring提供了声明式事务管理和编程式事务管理两种方式。通常,我们使用声明式事务管理,因为它更简洁且易于维护。 1. 声明式事务管理 声明式事务管理是通过注解来实现的。…...

深度学习-神经机器翻译模型
以下为你介绍使用Python和深度学习框架Keras(基于TensorFlow后端)实现一个简单的神经机器翻译模型的详细步骤和代码示例,该示例主要处理英 - 法翻译任务。 1. 安装必要的库 首先,确保你已经安装了以下库: pip insta…...

.NET周刊【2月第1期 2025-02-02】
国内文章 dotnet 9 已知问题 默认开启 CET 导致进程崩溃 https://www.cnblogs.com/lindexi/p/18700406 本文记录 dotnet 9 的一个已知且当前已修问题。默认开启 CET 导致一些模块执行时触发崩溃。 dotnet 使用 ColorCode 做代码着色器 https://www.cnblogs.com/lindexi/p/…...
【合集】Java进阶——Java深入学习的笔记汇总 amp; 再论面向对象、数据结构和算法、JVM底层、多线程
前言 spring作为主流的 Java Web 开发的开源框架,是Java 世界最为成功的框架,持续不断深入认识spring框架是Java程序员不变的追求;而spring的底层其实就是Java,因此,深入学习Spring和深入学习Java是硬币的正反面&…...

GPU、CUDA 和 cuDNN 学习研究【笔记】
分享自己在入门显存优化时看过的一些关于 GPU 和 CUDA 和 cuDNN 的网络资料。 更多内容见: Ubuntu 22.04 LTS 安装 PyTorch CUDA 深度学习环境-CSDN博客CUDA 计算平台 & CUDA 兼容性【笔记】-CSDN博客 文章目录 GPUCUDACUDA Toolkit都包含什么?NVID…...

【5】阿里面试题整理
[1]. 介绍一下ZooKeeper ZooKeeper是一个开源的分布式协调服务,核心功能是通过树形数据模型(ZNode)和Watch机制,解决分布式系统的一致性问题。 它使用ZAB协议保障数据一致性,典型场景包括分布式锁、配置管理和服务注…...

计算机毕业设计hadoop+spark+hive物流预测系统 物流大数据分析平台 物流信息爬虫 物流大数据 机器学习 深度学习
温馨提示:文末有 CSDN 平台官方提供的学长联系方式的名片! 温馨提示:文末有 CSDN 平台官方提供的学长联系方式的名片! 温馨提示:文末有 CSDN 平台官方提供的学长联系方式的名片! 作者简介:Java领…...
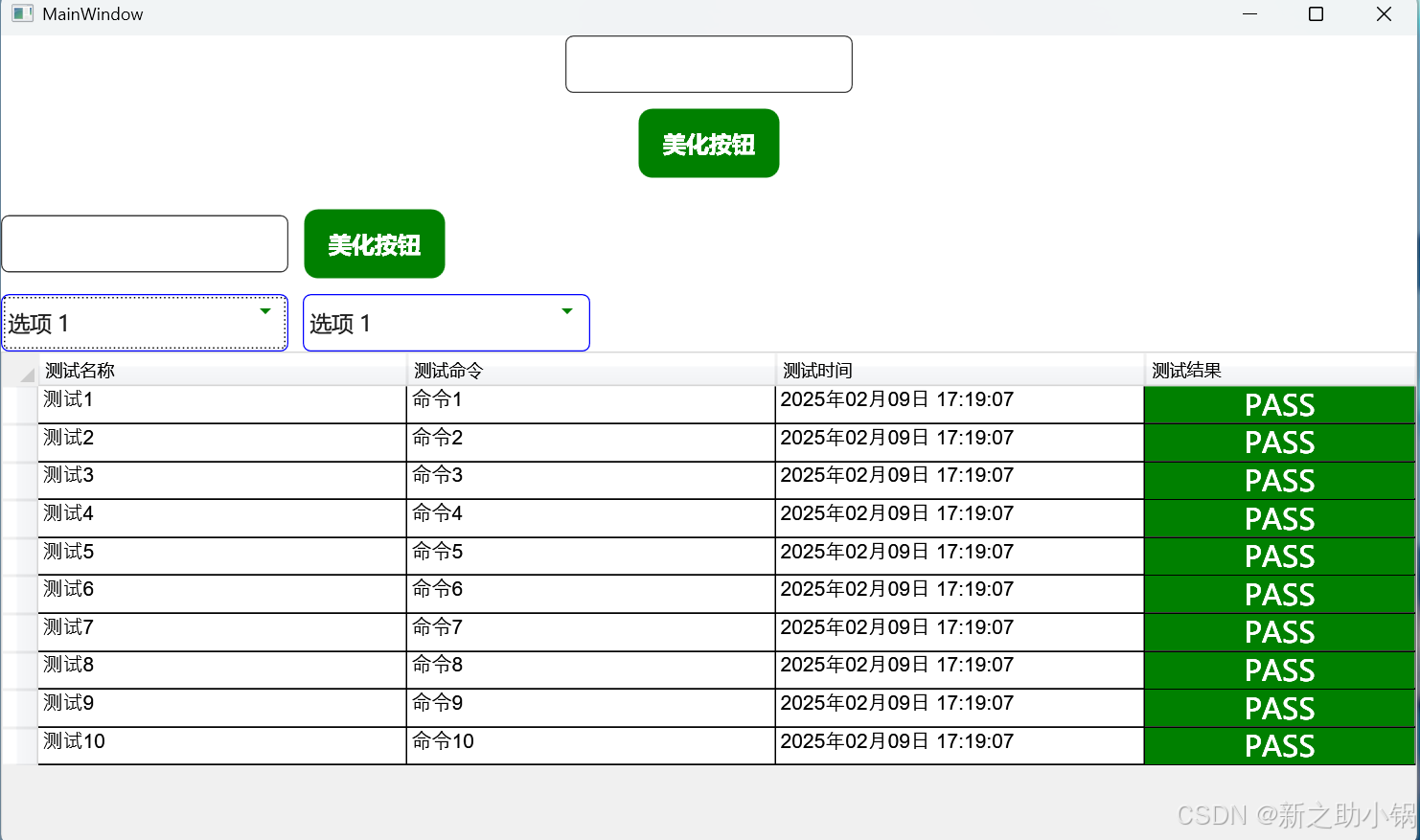
Wpf美化按钮,输入框,下拉框,dataGrid
Wpf美化按钮,输入框,下拉框,dataGrid 引用代码后 引用资源 <ControlTemplate x:Key"CustomProgressBarTemplate" TargetType"ProgressBar"><Grid><Border x:Name"PART_Track" CornerRadius&q…...

搜索插入位置:二分查找的巧妙应用
问题描述 给定一个已排序的整数数组 nums 和一个目标值 target,要求在数组中找到目标值并返回其索引。如果目标值不存在于数组中,则返回它按顺序插入的位置。必须使用时间复杂度为 O(log n) 的算法。 示例: 示例1: 输入: nums …...

Cocos2d-x 游戏开发-打包apk被默认自带了很多不必要的权限导致apk被报毒,如何在Cocos 2d-x中强制去掉不必要的权限-优雅草卓伊凡
Cocos2d-x 游戏开发-打包apk被默认自带了很多不必要的权限导致apk被报毒,如何在Cocos 2d-x中强制去掉不必要的权限-优雅草卓伊凡 实战操作 去除权限 要在 Cocos2d-x 开发的游戏中去掉 APK 自带权限,可以按照以下步骤操作: 编辑 AndroidMa…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...

第7篇:中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中,可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中,必须做到: 🔍 追踪每一条 SQL 的生命周期(从入口到数据库执行)&#…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...
