数据结构:图论入门
图论起源于欧拉对哥尼斯堡七桥问题的解决. 他构建的图模型将陆地用点来表示, 桥梁则用线表示, 如此一来, 该问题便转化为在图中能否不重复地遍历每条边的问题.
图论的应用
地图着色
在地图着色问题中, 我们用顶点代表国家, 将相邻国家之间用边相连. 这样, 问题就转化为用最少的颜色给图的顶点着色, 同时要保证相邻顶点的颜色不同. 四色定理表明, 任何地图都可以用四种颜色进行着色.
频率分配
以顶点表示发射机, 将干扰范围内的发射机之间用边相连. 频率分配问题就可以转化为给顶点标记数字, 使得相邻顶点标记的数字差值尽可能大.
燃气供应
利用平面图进行建模, 其中顶点表示路口, 边表示道路, 面表示区域. 通过寻找最小面生成子图, 能够确定铺设燃气管道的最优道路网络, 从而实现成本的最小化.
布局规划
在 VLSI(超大规模集成电路)和建筑布局规划中, 用图来表示模块或房间之间的连接关系. 通过对平面图进行三角剖分, 构建对偶图并绘制矩形图, 从而得到布局方案.
其他应用
图论还广泛应用于万维网社区发现, 生物信息学(如 RNA 结构描述), 软件工程(如控制流图用于软件测试)等诸多领域.
图的基本概念
图的定义
图(Graph)
一个图 G G G由两个集合组成, 即顶点集 V ( G ) V(G) V(G)和边集 E ( G ) E(G) E(G), 通常记为 G = ( V , E ) G=(V, E) G=(V,E). 顶点(Vertex, 也称为节点 Node)是图的基本元素, 用于表示研究的对象; 边(Edge)是连接两个顶点的线, 用于表示对象之间的关系. 若图中无自环边( 从 v v v 到 v v v ) 且无重边(两个节点之间存在多条边), 则为简单图, 反之则为多重图.
顶点(Vertex)
顶点是图中的基本元素, 即图的节点. 顶点可以有自己的属性, 例如在社交网络的图模型中, 顶点代表用户, 每个顶点可能包含用户的年龄, 性别等属性信息.
边(Edge)
边是连接两个顶点的线. 根据边是否有方向, 图可分为无向图和有向图. 在无向图中, 边没有方向, 若顶点 u u u和 v v v之间有边, 则表示为 ( u , v ) (u, v) (u,v), 且 ( u , v ) (u, v) (u,v)和 ( v , u ) (v, u) (v,u)表示同一条边; 在有向图中, 边有方向, 从顶点 u u u指向顶点 v v v的边表示为 ( u , v ) (u, v) (u,v), 它与从 v v v指向 u u u的边 ( v , u ) (v, u) (v,u)是不同的边.
邻接(Adjacency)
在无向图中, 如果两个顶点 u u u和 v v v之间有一条边 ( u , v ) (u, v) (u,v), 则称顶点 u u u和 v v v是邻接的; 在有向图中, 如果存在一条从顶点 u u u到顶点 v v v的有向边 ( u , v ) (u, v) (u,v), 则称顶点 u u u邻接到顶点 v v v, 顶点 v v v邻接自顶点 u u u.
度(Degree)
对于无向图中的一个顶点 v v v, 它的度是与该顶点相关联的边的数量, 记为 d ( v ) d(v) d(v); 在有向图中, 顶点的度分为入度和出度. 入度(In - degree)是指以该顶点为终点的有向边的数量, 记为 d − ( v ) d^-(v) d−(v), 出度(Out - degree)是指以该顶点为起点的有向边的数量, 记为 d + ( v ) d^+(v) d+(v), 顶点 v v v的度等于其入度与出度之和, 即 d ( v ) = d − ( v ) + d + ( v ) d(v)=d^-(v) + d^+(v) d(v)=d−(v)+d+(v).
路径(Path)
在图中, 从一个顶点 v 0 v_0 v0开始, 依次经过一系列相邻的顶点 v 1 , v 2 , ⋯ , v n v_1, v_2, \cdots, v_n v1,v2,⋯,vn所形成的顶点序列, 其中 ( v i − 1 , v i ) ∈ E (v_{i - 1}, v_i) \in E (vi−1,vi)∈E(对于无向图)或 ( v i − 1 , v i ) ∈ E (v_{i - 1}, v_i) \in E (vi−1,vi)∈E(对于有向图, i = 1 , 2 , ⋯ , n i = 1, 2, \cdots, n i=1,2,⋯,n), 这个顶点序列就称为从 v 0 v_0 v0到 v n v_n vn的路径. 路径中边的数量称为路径的长度.
回路(Cycle)
在图中, 起点和终点相同的路径称为回路, 也叫环. 也就是说, 如果路径 v 0 , v 1 , ⋯ , v n v_0, v_1, \cdots, v_n v0,v1,⋯,vn满足 v 0 = v n v_0 = v_n v0=vn且 n ≥ 1 n \geq 1 n≥1, 则它是一个回路.
连通图(Connected Graph)
在无向图中, 如果对于图中的任意两个顶点 u u u和 v v v, 都存在一条从 u u u到 v v v的路径, 则称该图是连通图; 在有向图中, 如果对于图中的任意两个顶点 u u u和 v v v, 都存在从 u u u到 v v v的路径以及从 v v v到 u u u的路径, 则称该有向图是强连通图. 如果一个有向图不是强连通图, 但忽略边的方向后得到的无向图是连通图, 则称该有向图是弱连通图.
子图(Subgraph)
给定一个图 G = ( V , E ) G=(V, E) G=(V,E), 如果存在另一个图 G ′ = ( V ′ , E ′ ) G'=(V', E') G′=(V′,E′), 其中 V ′ ⊆ V V'\subseteq V V′⊆V( V ′ V' V′是 V V V的子集)且 E ′ ⊆ E E'\subseteq E E′⊆E( E ′ E' E′是 E E E的子集), 并且 E ′ E' E′中的边所关联的顶点都在 V ′ V' V′中, 则称 G ′ G' G′是 G G G的子图.
树(Tree)
无向连通且无回路的图称为树. 树中度数为 1 的顶点称为叶子节点, 其他顶点称为内部节点. 在树中, 任意两个顶点之间恰好存在一条路径. 有根树是一种特殊的树, 它有一个被指定为根的顶点, 从根到其他顶点有唯一的路径.
图的分类
正则图
所有顶点度相等的图是正则图, 当度为 k k k时, 称为 k − k - k−正则图. 例如, 零图是 0 − 0 - 0−正则图, 简单循环是 2 − 2 - 2−正则图, 彼得森图是 3 − 3 - 3−正则图, 还有 5 − 5 - 5−正则的甜甜圈图和 d − d - d−维超立方体等.
子图
图 G = ( V , E ) G=(V, E) G=(V,E)的子图 G ′ = ( V ′ , E ′ ) G'=(V', E') G′=(V′,E′)满足 V ′ ⊆ V V' \subseteq V V′⊆V且 E ′ ⊆ E E' \subseteq E E′⊆E. 可以通过删除顶点或边得到子图, 如 G − e G - e G−e, G − v G - v G−v . 还有顶点集或边集诱导的子图, 如 G [ W ] G[W] G[W] , G [ F ] G[F] G[F] .
特殊图类
包括空图(边集为空, 记为 N n N_{n} Nn ), 完全图(任意两顶点相邻, K n K_{n} Kn有 n ( n − 1 ) / 2 n(n - 1)/2 n(n−1)/2条边), 独立集和二分图(顶点集可分成两个独立子集, 完全二分图 K m , n K_{m,n} Km,n有 m × n m×n m×n条边), 路径图( P n P_{n} Pn除端点外顶点度为 2 ), 循环图( C n C_{n} Cn所有顶点度为 2 ), 轮图( W n W_{n} Wn由 C n − 1 C_{n - 1} Cn−1加新顶点连接所有 C n − 1 C_{n - 1} Cn−1顶点得到).
图的操作
图的运算
- 集合运算: 图 G 1 G_{1} G1和 G 2 G_{2} G2的并集 G 1 ∪ G 2 G_{1} \cup G_{2} G1∪G2顶点集为 V 1 ∪ V 2 V_{1} \cup V_{2} V1∪V2 , 边集为 E 1 ∪ E 2 E_{1} \cup E_{2} E1∪E2; 交集 G 1 ∩ G 2 G_{1} \cap G_{2} G1∩G2顶点集为 V 1 ∩ V 2 V_{1} \cap V_{2} V1∩V2 , 边集为 E 1 ∩ E 2 E_{1} \cap E_{2} E1∩E2 .
- 其他运算: 图 G G G的补图 G ˉ \bar{G} Gˉ与 G G G顶点集相同, 两顶点在 G ˉ \bar{G} Gˉ中有边当且仅当在 G G G中无边; 细分是删边并通过新顶点添加路径; 收缩边是删边并合并两顶点.
图同构
图 G 1 G_{1} G1和 G 2 G_{2} G2间存在一一对应关系, 使对应顶点间边数相等, 则两图同构, 记为 G 1 ≅ G 2 G_{1} \cong G_{2} G1≅G2 . 同构关系是等价关系, 判断图同构目前尚无多项式时间算法.
度序列
图的度序列是顶点度的非增排列, 满足度和公式(和为偶数)的序列可能是图的度序列, 简单图的度序列叫图序列, 可通过递归算法判断.
数据结构与图的表示
邻接矩阵
邻接矩阵是 n × n n×n n×n矩阵, 元素为两顶点间边数, 简单图邻接矩阵元素为 0 或 1 , 主对角线为 0 , 空间复杂度 O ( n 2 ) O(n^{2}) O(n2) ; 关联矩阵是 n × m n×m n×m矩阵, 元素表示顶点与边是否关联, 空间复杂度 n × m n×m n×m ; 邻接表是数组, 每个顶点对应一个包含其邻居记录的列表, 空间复杂度 O ( n + m ) O(n + m) O(n+m) .
邻接表
用数组存储顶点的邻接顶点列表, 空间复杂度 O ( n + m ) O(n + m) O(n+m) , 适用于边数较少的图.
相关文章:

数据结构:图论入门
图论起源于欧拉对哥尼斯堡七桥问题的解决. 他构建的图模型将陆地用点来表示, 桥梁则用线表示, 如此一来, 该问题便转化为在图中能否不重复地遍历每条边的问题. 图论的应用 地图着色 在地图着色问题中, 我们用顶点代表国家, 将相邻国家之间用边相连. 这样, 问题就转化为用最少…...

有限状态系统的抽象定义及CEGAR分析解析理论篇
文章目录 一、有限状态系统的抽象定义及相关阐述1、有限状态系统定义2、 有限状态系统间的抽象关系(Abstract)2.1 基于函数的抽象定义2.2 基于等价关系的抽象定义 二、 基于上面的定义出发,提出的思考1. 为什么我们想要/需要进行抽象2. 抽象是…...

Apache Hive用PySpark统计指定表中各字段的空值、空字符串或零值比例
from pyspark.sql import SparkSession from pyspark.sql.functions import col, coalesce, trim, when, lit, sum from pyspark.sql.types import StringType, NumericType# 初始化SparkSession spark SparkSession.builder \.appName("Hive Data Quality Analysis"…...

高校元宇宙实训室解决方案:以技术驱动教育,用数字人链接未来
在AIGC技术的浪潮下,AI数字人正成为数字营销、文化传播等领域的核心工具。为助力高校培养适应未来需求的新型人才,广州虚拟动力推出高校元宇宙实训室解决方案,通过动作捕捉设备与虚拟数字人技术,构建沉浸式教学场景,赋…...

提升编程效率,体验智能编程助手—豆包MarsCode一键Apply功能测评
提升编程效率,体验智能编程助手—豆包MarsCode一键Apply功能测评 🌟 嗨,我是LucianaiB! 🌍 总有人间一两风,填我十万八千梦。 🚀 路漫漫其修远兮,吾将上下而求索。 目录 引言豆包…...

【前端开发】query参数和params参数的区别
在Web开发中,query参数(URL查询参数)和params参数(路由参数)是两种不同的URL传参方式,它们的核心区别如下: 一、 位置不同 query参数params参数位置URL中?之后,用&连接多个参数…...

推荐系统召回算法
推荐系统召回算法 召回算法UserCFItemCFSwing矩阵分解 召回算法 基于协同过滤的召回算法主要是应用在推荐环节的早期阶段,大致可以分为基于用户、基于物品的。两者各有优劣,优点是具有较好的可解释性,缺点是对于稀疏的交互矩阵,效…...
)
Python基础(上)
1. 基础语法 1.1 环境安装 Python版本: 推荐使用Python 3.6.6及以上开发工具: PyCharm 1.2 基本语法 输出: print("Hello World") 注释: 单行注释: # 注释内容(快捷键 Ctrl/) 多行注释: 使用三引号 注释内容 注意:不推…...

【DuodooBMS】给PDF附件加“受控”水印的完整Python实现
给PDF附件加“受控”水印的完整Python实现 功能需求 在实际工作中,许多文件需要添加水印以标识其状态,例如“受控”“机密”等。对于PDF文件,添加水印不仅可以增强文件的可识别性,还可以防止未经授权的使用。本代码的功能需求是…...

【虚幻引擎UE】UE4.23到UE5.5的核心功能变化
简单总结从UE4.23到UE5.5,虚幻引擎的重大变化: 1. WebGL/HTML5 平台支持和像素流 UE4.23-UE4.25:移除官方HTML5支持,改为社区插件维护。 但通过第三方插件(如WebAssemblyWebGPU)可在浏览器运行部分项目。U…...

阿里云《AI 剧本生成与动画创作》解决方案技术评测
引言 随着人工智能技术的发展,越来越多的工具和服务被应用于内容创作领域。阿里云推出的《AI 剧本生成与动画创作》解决方案,利用函数计算 FC 构建 Web 服务,结合百炼模型服务和 ComfyUI 工具,实现了从故事剧本撰写、插图设计、声…...

commons-io 包 IOUtils、FileUtils、FilenameUtils
1. IOUtils void IOUtils.closeQuietly(Closeable... closeables) 无条件关闭流。int IOUtils.copy(InputStream inputStream, OutputStream outputStream) 将字节从InputStream复制到OutputStream,返回复制的长度,流最大不能超过2G,默认缓冲…...

JavaScript 加密技术全面指南
一、加密技术概述 在现代 Web 开发中,加密技术在保护用户数据和确保信息安全方面发挥着至关重要的作用。本文将带您了解 JavaScript 加密技术的基本概念、分类及其在实际应用中的场景。 加密的基本概念 加密是一种将明文数据转换为密文的技术,以保护数…...

【笔记】deep-seek wechat项目
1、安装ollama ollama官网 2、ollama上部署deepseek ollama官网下载deepseek模型(我下了1.5B) 3、配置python 国内镜像源 pip config set global.index-url https://mirrors.aliyun.com/pypi/simple/ 安装依赖包 pip install wxauto pip instal…...

FloodFill算法——搜索算法
一、什么是FloodFill算法 FloodFill算法字面意思就是洪水灌溉法,比如我们有这么一块地: 0表示平原,正数表示高地,负数表示凹地,那么当洪水来临时这些凹地会被优先灌满。而我们要找的正是这些联通块,如&…...

H5接入支付宝手机网站支付并实现
小程序文档 - 支付宝文档中心 1.登录 支付宝开放平台 创建 网页/移动应用 2.填写创建应用信息 3.配置开发设置 4.网页/移动应用:需要手动上线。提交审核后,预计 1 个工作日的审核时间。详细步骤可点击查看 上线应用 。应用上线后,还需要完成…...

基于SpringBoot+uniapp的在线办公小程序+LW示例参考
1.项目介绍 系统角色:管理员、普通用户功能模块:员工管理、部门信息管理、职位信息管理、会议记录、待办事项、工资信息、留言板等技术选型:SpringBoot,Vue(后端管理web),uniapp等测试环境&…...

文章精读篇——OMG-LLaVA
题目:OMG-LLaVA: Bridging Image-level, Object-level, Pixel-level Reasoning and Understanding 会议:Conference on Neural Information Processing Systems 2024 论文:http://arxiv.org/abs/2406.19389 主页:https://lxtgh…...

两个同一对象targetList和 sourceList 去重
我现在需要解决的问题是从一个Java的源列表`sourceList`中移除所有在目标列表`targetList`中存在的数据,并且还要去除`targetList`中的重复数据。让我先理清楚这两个问题的思路。 首先,如何快速从`sourceList`中移除含有`targetList`的数据。这里的“含有”应该是指两个列表中…...

软件开发 | GitHub企业版常见问题解读
什么是GitHub企业版? GitHub企业版是一个企业级软件开发平台,专为现代化开发的复杂工作流程而设计。 作为可扩展的平台解决方案,GitHub企业版使组织能够无缝集成其他工具和功能,并根据特定需求定制开发环境,提高整体…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...

【SpringBoot自动化部署】
SpringBoot自动化部署方法 使用Jenkins进行持续集成与部署 Jenkins是最常用的自动化部署工具之一,能够实现代码拉取、构建、测试和部署的全流程自动化。 配置Jenkins任务时,需要添加Git仓库地址和凭证,设置构建触发器(如GitHub…...

【Linux手册】探秘系统世界:从用户交互到硬件底层的全链路工作之旅
目录 前言 操作系统与驱动程序 是什么,为什么 怎么做 system call 用户操作接口 总结 前言 日常生活中,我们在使用电子设备时,我们所输入执行的每一条指令最终大多都会作用到硬件上,比如下载一款软件最终会下载到硬盘上&am…...
之(六) ——通用对象池总结(核心))
怎么开发一个网络协议模块(C语言框架)之(六) ——通用对象池总结(核心)
+---------------------------+ | operEntryTbl[] | ← 操作对象池 (对象数组) +---------------------------+ | 0 | 1 | 2 | ... | N-1 | +---------------------------+↓ 初始化时全部加入 +------------------------+ +-------------------------+ | …...

如何把工业通信协议转换成http websocket
1.现状 工业通信协议多数工作在边缘设备上,比如:PLC、IOT盒子等。上层业务系统需要根据不同的工业协议做对应开发,当设备上用的是modbus从站时,采集设备数据需要开发modbus主站;当设备上用的是西门子PN协议时…...
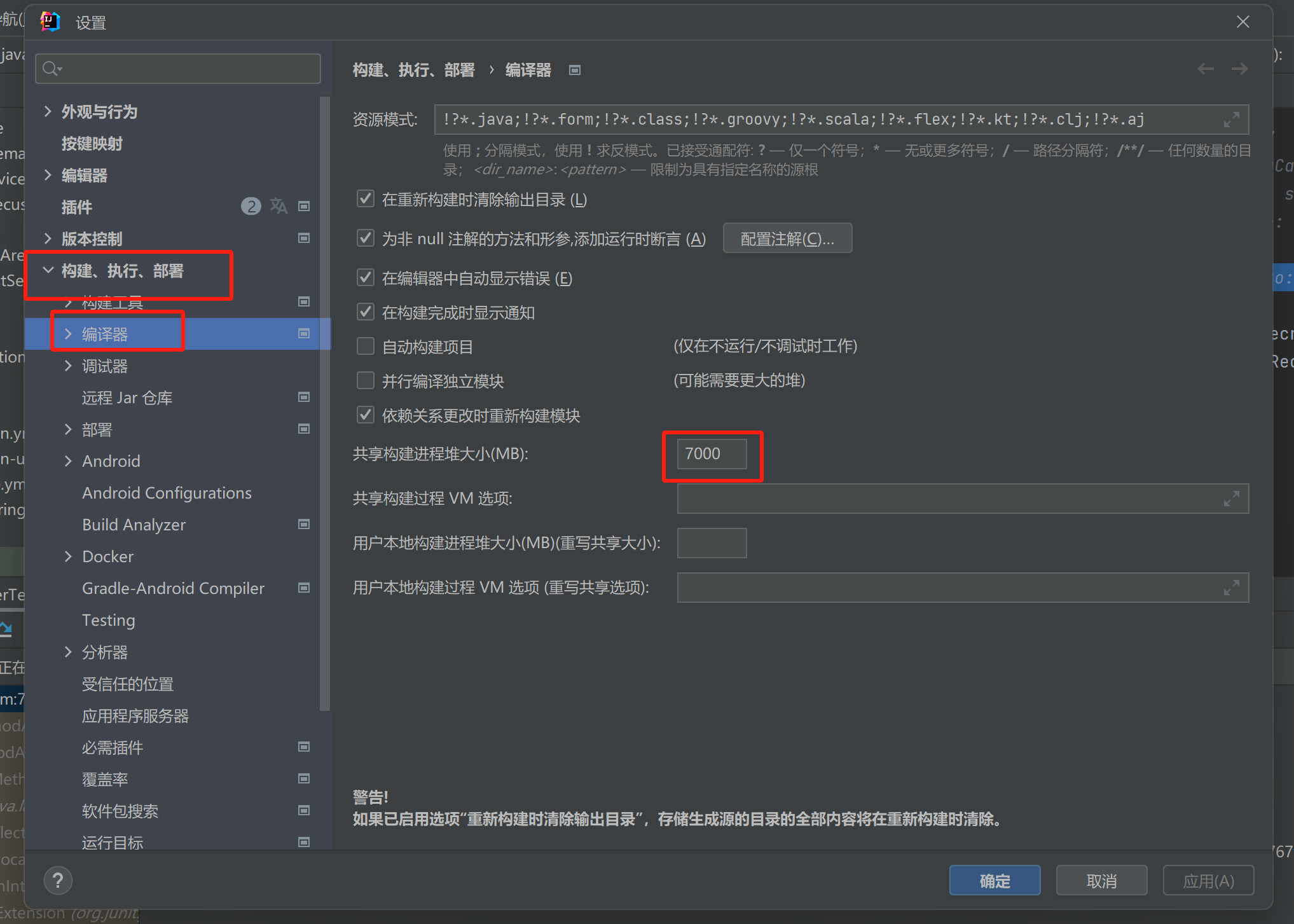
【记录坑点问题】IDEA运行:maven-resources-production:XX: OOM: Java heap space
问题:IDEA出现maven-resources-production:operation-service: java.lang.OutOfMemoryError: Java heap space 解决方案:将编译的堆内存增加一点 位置:设置setting-》构建菜单build-》编译器Complier...

【Vue】scoped+组件通信+props校验
【scoped作用及原理】 【作用】 默认写在组件中style的样式会全局生效, 因此很容易造成多个组件之间的样式冲突问题 故而可以给组件加上scoped 属性, 令样式只作用于当前组件的标签 作用:防止不同vue组件样式污染 【原理】 给组件加上scoped 属性后…...
