碎碎念,再聊HyperRAM(CrosslinkNX FPGA+HyperRAM)
作者:Hello,Panda
HyperRAM其实熊猫君很久以前在用了,几年前也分享了一篇实现HyperRAM控制器的博文(博文《Lattice CrossLinkNx LIFCL-40应用连载7-使用HyperRAM存储器》。近期在后台收到好几位朋友咨询一些关于HyperRAM的问题,熊猫君在这里简单的做一个总结。
一、什么是HyperRAM,有什么特点?
(1)技术本质:HyperRAM实际上是一个结合体,它的存储单元是PSRAM(伪静态RAM:它的存储器阵列内部结构类似于 DRAM,但在外部却像SRAM一样运作),接口是HyperBUS,一结合就是HyperRAM。
(2)从哪里来:HyperRAM技术是Cypress(现在被英飞凌收购)在2014发明的,从2015年起开始量产,随后华邦、ISSI等厂商开始跟进推出各自产品。也存在和SPI Flash封装在一起的MCP器件,目前已经发展到16bit位宽的HyperRAM3.0版本。
(3)技术特色:关键技术优势有两个:a)低功耗,静态功耗普遍低于50mW,全速访问功耗也不高;b)HyperBus接口少,比如一个16bit的HyperRAM3.0器件最多只需要21个IO。因此在要求IO占用少,容量和带宽要求适中,有严格功耗限制的场合特别适用。
二、应用场景
结合其技术特色可知,它主要用于低功耗长待机且缓存容量要求较大的场合:
(1)物联网:AIoT领域,特别是需要做触发式音视频和高精度ADC数据样本采集的场合,运营商提供的数据带宽往往无法瞬时上传采集到的数据,低功耗SoC(MCU)内部缓存又不够用时,常常会搭载一颗HyperRAM。
(2)可穿戴设备:特别是健康检测(体征检测)类的应用。
(3)工业设备:很多工业控制和自动化设备里面用到,还有就是热敏感的设备,如红外热成像,国内的一些红外热成像组件和探测器厂商常常会把HyperRAM和低功耗FPGA封装或组合在一起形成低功耗的SoC机芯产品以降低功耗,减少热串扰且提升性能(NETD)。
三、技术方案
技术方案其实就是低功耗的MCU(SoC)或低功耗的FPGA搭配。熊猫君有几块板子就采用了Lattice低功耗FPGA搭配HyperRAM的做法。如下图(1)HyperRAM2.0 8bit位宽的器件,型号是华邦的W958D8NBYA5I,低功耗FPGA是Lattice CrosslinkNX LIFCL-40-7MG121I。图(2)HyperRAM3.0 16bit位宽的器件,型号是华邦的W959D6NFKX[512Mb,16bit,250MHz运行频率],低功耗FPGA是Lattice自带USB3.2 Gen1 PHY的LIFCL-33U-8CTG104C。

图(1) HyperRAM2.0器件

图(2)HyperRAM3.0器件
后台私信留言留邮箱可从熊猫君处获取HyperRAM控制器Verilog源代码。
至于和低功耗MCU(SoC)的搭配方式,自不用多说,这些MCU(SoC)都自带HyperRAM控制器。配置参数使用即可。
今天熊猫君的分享到此结束。
相关文章:

碎碎念,再聊HyperRAM(CrosslinkNX FPGA+HyperRAM)
作者:Hello,Panda HyperRAM其实熊猫君很久以前在用了,几年前也分享了一篇实现HyperRAM控制器的博文(博文《Lattice CrossLinkNx LIFCL-40应用连载7-使用HyperRAM存储器》。近期在后台收到好几位朋友咨询一些关于HyperRAM的问题&a…...

左移架构 -- 从攒批,湖仓到使用数据流的实时数据产品
编辑导读: 这篇文章翻译自 Kai Waehner的 《The Shift Left Architecture – From Batch and Lakehouse to Real-Time Data Products with Data Streaming》。文章通过数据产品的概念引出了如何创建可重复使用的数据产品使企业能够从当前和未来的数据中获得价值。基于构建数据产…...

多模态识别和自然语言处理有什么区别
在科技飞速发展的当下,人工智能(AI)已经渗透到我们生活的方方面面。不知道大家有没有这样的经历:早上醒来,对着智能音箱说 “播放今天的新闻”,音箱不仅能识别你的语音,还能在播放新闻的同时&am…...
)
进阶——第十六蓝桥杯嵌入式熟练度练习(串口的小BUG补充-字符接受不完整和字符接受错误)
1.解决接受不完整问题 假如没接受完成,执行函数,就可能会把count直接清零,就会重新接受\ while (1){if(rx_count!0){uint8_t temprx_count;HAL_Delay(1);if(temprx_count)uart_proc(); }key_proc();rxclear_proc();/* USER CODE END WHILE…...

数据结构-链式二叉树
文章目录 一、链式二叉树1.1 链式二叉树的创建1.2 根、左子树、右子树1.3 二叉树的前中后序遍历1.3.1前(先)序遍历1.3.2中序遍历1.3.3后序遍历 1.4 二叉树的节点个数1.5 二叉树的叶子结点个数1.6 第K层节点个数1.7 二叉树的高度1.8 查找指定的值(val)1.9 二叉树的销毁 二、层序…...

【git-hub项目:YOLOs-CPP】本地实现01:项目构建
目录 写在前面 项目介绍 最新发布说明 Segmentation示例 功能特点 依赖项 安装 克隆代码仓库 配置 构建项目 写在前面 前面刚刚实现的系列文章: 【Windows/C++/yolo开发部署01】 【Windows/C++/yolo开发部署02】 【Windows/C++/yolo开发部署03】 【Windows/C++/yolo…...

250213-RHEL8.8-外接SSD固态硬盘
It seems that the exfat-utils package is still unavailable, even after enabling the RPM Fusion repository. This could happen if the repository metadata hasn’t been updated or if the package isn’t directly available in the RPM Fusion repository for RHEL 8…...

如何本地部署DeepSeek?
DeepSeek:智能时代的得力助手 在人工智能技术飞速发展的今天,DeepSeek 作为一款由国内顶尖团队研发的 AI 工具,凭借其卓越的性能和丰富的功能,逐渐在众多同类产品中脱颖而出,成为众多用户在工作和学习中的得力助手。 …...

leetcode:627. 变更性别(SQL解法)
难度:简单 SQL Schema > Pandas Schema > Salary 表: ----------------------- | Column Name | Type | ----------------------- | id | int | | name | varchar | | sex | ENUM | | salary | int …...

51单片机(国信长天)矩阵键盘的基本操作
在CT107D单片机综合训练平台上,首先将J5处的跳帽接到1~2引脚,使按键S4~S19按键组成4X4的矩阵键盘。在扫描按键的过程中,发现有按键触发信号后(不做去抖动),待按键松开后,在数码管的第一位显示相应的数字:从左至右&…...

封装一个sqlite3动态库
作者:小蜗牛向前冲 名言:我可以接受失败,但我不能接受放弃 如果觉的博主的文章还不错的话,还请点赞,收藏,关注👀支持博主。如果发现有问题的地方欢迎❀大家在评论区指正 目录 一、项目案例 二…...

Transformer以及BERT阅读参考博文
Transformer以及BERT阅读参考博文 Transformer学习: 已有博主的讲解特别好了: 李沐:Transformer论文逐段精读【论文精读】_哔哩哔哩_bilibili知乎:Transformer模型详解(图解最完整版) - 知乎 个人杂想&…...

AI学习记录 - 最简单的专家模型 MOE
代码 import torch import torch.nn as nn import torch.nn.functional as F from typing import Tupleclass BasicExpert(nn.Module):# 一个 Expert 可以是一个最简单的, linear 层即可# 也可以是 MLP 层# 也可以是 更复杂的 MLP 层(active function 设…...

急停信号的含义
前言: 大家好,我是上位机马工,硕士毕业4年年入40万,目前在一家自动化公司担任软件经理,从事C#上位机软件开发8年以上!我们在开发C#的运动控制程序的时候,一个必要的步骤就是确认设备按钮的急停…...

单调队列queue
1.单调队列(Monotonic Queue) 单调队列是一种特殊的队列,它的元素按照单调性(递增或递减)的顺序排列。简单来说,单调队列会维护一个元素单调递增或递减的顺序,在队列中元素会根据当前队列的元素…...
【漫话机器学习系列】091.置信区间(Confidence Intervals)
置信区间(Confidence Intervals)详解 1. 引言 在统计学和数据分析中,我们通常希望通过样本数据来估计总体参数。然而,由于抽样的随机性,我们不可能得到精确的总体参数,而只能通过估计值(如均值…...

UnicodeDecodeError: ‘gbk‘ codec can‘t decode byte 0x99
UnicodeDecodeError: ‘gbk’ codec can’t decode byte 0x99 这个错误通常发生在你尝试使用 GBK 编码来解码一个包含非GBK编码字符的文件时。GBK 是一种用于简体中文的字符编码方式,它不支持所有可能的 Unicode 字符。 解决方法 明确文件的正确编码:首…...

DeepSeek应用——与word的配套使用
目录 一、效果展示 二、配置方法 三、使用方法 四、注意事项 1、永久化使用 2、宏被禁用 3、office的生成失败 记录自己学习应用DeepSeek的过程...... 这个是与WPS配套使用的过程,office的与这个类似: 一、效果展示 二、配置方法 1、在最上方的…...

递归乘法算法
文章目录 递归乘法题目链接题目详解解题思路:代码实现: 结语 欢迎大家阅读我的博客,给生活加点impetus!! 让我们进入《题海探骊》,感受算法之美!! 递归乘法 题目链接 在线OJ 题目…...
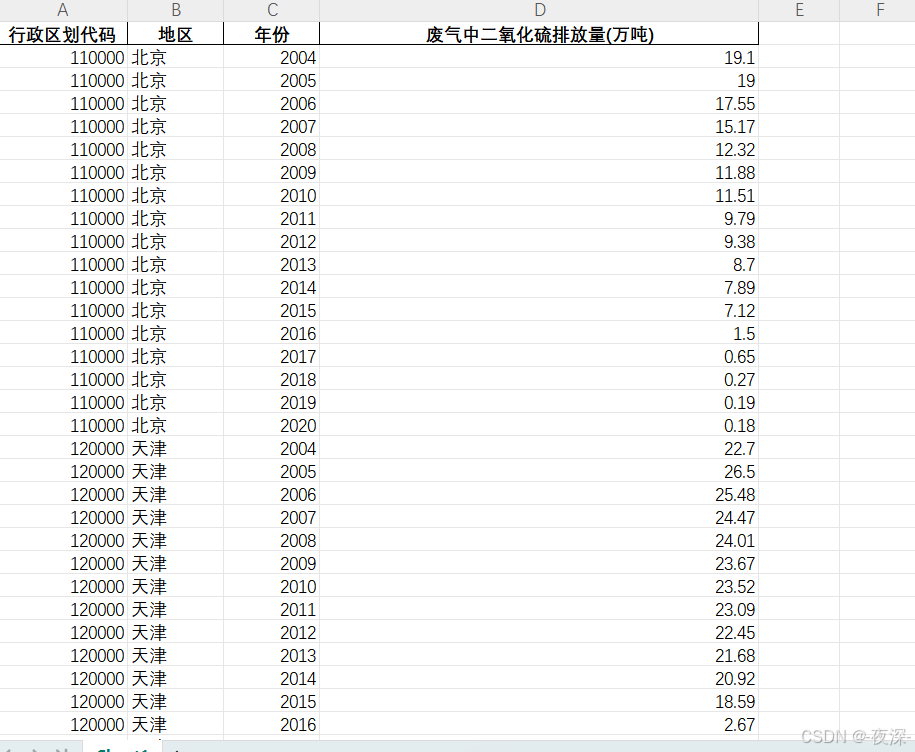
【免费】2004-2020年各省废气中废气中二氧化硫排放量数据
2004-2020年各省废气中废气中二氧化硫排放量数据 1、时间:2004-2020年 2、来源:国家统计局、统计年鉴 3、指标:行政区划代码、地区、年份、废气中二氧化硫排放量(万吨) 4、范围:31省 5、指标说明:二氧化硫排放量指…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...
