单调队列queue
1.单调队列(Monotonic Queue)
单调队列是一种特殊的队列,它的元素按照单调性(递增或递减)的顺序排列。简单来说,单调队列会维护一个元素单调递增或递减的顺序,在队列中元素会根据当前队列的元素和新加入的元素来进行更新。
基本概念
-
单调递增队列:
- 对于每个进入队列的元素,队列中的元素始终保持递增(从队头到队尾)。
- 如果新元素小于队尾元素,队尾元素会被弹出,直到新元素大于或等于队尾元素。
-
单调递减队列:
- 与递增队列相反,队列中的元素始终保持递减(从队头到队尾)。
- 如果新元素大于队尾元素,队尾元素会被弹出,直到新元素小于或等于队尾元素。
应用场景
-
滑动窗口问题:
- 常用于处理一些滑动窗口的最大值或最小值问题。
- 如:给定一个数组,要求求出每个大小为k的滑动窗口内的最大值或最小值。
-
范围查询:
- 在一些区间问题中,可以通过单调队列高效地维护某些信息,如最大值或最小值。
单调队列的基本操作
-
插入元素:新元素进入队列时,如果它不满足单调性,需要将队尾的元素弹出,直到队列中的元素保持单调性。
-
弹出元素:元素离开队列时,队头的元素会被弹出。
-
获取队头元素:队头元素即为当前队列中最值(最大值或最小值)。
基本的单调队列实现(滑动窗口最大值)
#include <iostream>
#include <deque>
#include <vector>
using namespace std;vector<int> maxSlidingWindow(vector<int>& nums, int k) {vector<int> result;deque<int> dq; // 存储窗口中的元素下标,队列是单调递减的for (int i = 0; i < nums.size(); i++) {// 弹出不在当前窗口内的元素if (!dq.empty() && dq.front() <= i - k) {dq.pop_front();}// 保持队列单调递减,弹出队尾小于当前元素的元素while (!dq.empty() && nums[dq.back()] <= nums[i]) {dq.pop_back();}// 将当前元素下标插入队列dq.push_back(i);// 当窗口大小达到 k 时,队头就是最大值if (i >= k - 1) {result.push_back(nums[dq.front()]);}}return result;
}int main() {vector<int> nums = {1,3,-1,-3,5,3,6,7};int k = 3;vector<int> res = maxSlidingWindow(nums, k);for (int num : res) {cout << num << " ";}cout << endl;return 0;
}
代码解释
-
队列维护:使用
deque<int> dq来存储窗口中元素的下标。- 维护队列是单调递减的,即队列的队头是当前窗口的最大值对应的下标。
-
窗口更新:
- 每当移动窗口时,先移除不在窗口内的元素(即下标小于
i - k + 1的元素)。 - 然后确保队列中的元素是单调递减的,弹出队尾小于当前元素的元素。
- 每当移动窗口时,先移除不在窗口内的元素(即下标小于
-
窗口内最大值:
- 当窗口的大小达到
k时,队头的元素对应的就是当前窗口的最大值,因此可以将nums[dq.front()]加入结果。
- 当窗口的大小达到
时间复杂度
-
时间复杂度:
O(n),其中n是数组的大小。每个元素最多入队一次,出队一次,因此时间复杂度是线性的。 -
空间复杂度:
O(k),队列最多存储k个元素的下标。
单调队列的拓展
除了在滑动窗口最大值问题中的应用,单调队列还可以应用于其他问题,下面是几个典型的扩展和优化。
1. 计算区间最小值/最大值
- 在给定区间内维护最大值或最小值,单调队列可以通过类似的方法帮助维护区间内的最值。
2. 单调队列解法的优化
- 优化查询和更新操作:一些问题中,查询操作和更新操作都可以在
O(1)时间内完成,而对于较大的区间,可以通过分块和双指针的技巧进一步优化。
3. 维护多个窗口的最大值/最小值
- 可以使用多个单调队列,分别维护不同的窗口的最值,从而满足多个窗口的查询要求。
4. 最小栈与最大栈的扩展
- 在实现栈的最大值或最小值时,可以使用单调队列来优化栈内的查询。
复杂度优化
- 空间优化:对于一些问题,我们可以通过双端队列的变种来优化空间复杂度,避免额外的空间浪费。
总结
- 单调队列是一个非常强大的工具,特别适用于维护动态区间的最大值或最小值,常用于解决滑动窗口相关问题。
- 它的核心思想是利用队列保持元素的单调性,从而在窗口或区间中高效地获取最值。
- 在滑动窗口问题中,单调队列的应用使得时间复杂度可以优化到
O(n),从而大大提高了效率。
2.题
1.算法竞赛进阶指南

思路:用bfs查找所有的方式
#include <iostream>
#include <vector>
#include <queue>
#include <unordered_map>using namespace std;const int N = 4;
char graph[N][N];
int target = 0; // 目标状态,所有手柄都打开// 将当前状态转换为整数
int stateToInt(const char graph[N][N]) {int state = 0;for (int i = 0; i < N; ++i) {for (int j = 0; j < N; ++j) {if (graph[i][j] == '-') {state |= (1 << (i * N + j));}}}return state;
}// 将整数转换回状态
void intToState(int state, char graph[N][N]) {for (int i = 0; i < N; ++i) {for (int j = 0; j < N; ++j) {graph[i][j] = (state & (1 << (i * N + j))) ? '-' : '+';}}
}// 翻转手柄 [x, y] 及其所在行和列的所有手柄
void toggle(char graph[N][N], int x, int y) {for (int i = 0; i < N; ++i) {if (graph[x][i] == '+') graph[x][i] = '-';else graph[x][i] = '+';if (graph[i][y] == '+') graph[i][y] = '-';else graph[i][y] = '+';}if (graph[x][y] == '+') graph[x][y] = '-';else graph[x][y] = '+';
}struct State {int state;vector<pair<int, int>> moves;
};int main() {// 读取输入for (int i = 0; i < N; ++i) {for (int j = 0; j < N; ++j) {cin >> graph[i][j];}}// 初始化目标状态target = (1 << (N * N)) - 1; // 所有手柄都打开的状态// 使用BFS寻找最短路径queue<State> q;unordered_map<int, bool> visited;int initialState = stateToInt(graph);q.push({initialState, {}});visited[initialState] = true;while (!q.empty()) {State current = q.front();q.pop();if (current.state == target) {cout << current.moves.size() << endl;for (auto& move : current.moves) {cout << move.first + 1 << " " << move.second + 1 << endl;}return 0;}for (int i = 0; i < N; ++i) {for (int j = 0; j < N; ++j) {char tempGraph[N][N];intToState(current.state, tempGraph);toggle(tempGraph, i, j);int nextState = stateToInt(tempGraph);if (!visited[nextState]) {visited[nextState] = true;auto newMoves = current.moves;newMoves.emplace_back(i, j);q.push({nextState, newMoves});}}}}return 0;
}
2.

思路:模板题
#include <iostream>
#include <vector>
#include <stack>
#include <algorithm>using namespace std;void func(vector<int>& nums) {vector<int>dis(nums.size(), 0);stack<int>st;for (int i = 0; i < nums.size(); i++) {while (!st.empty() && nums[i] > nums[st.top()]) {dis[st.top()] = i + 1;st.pop();}st.push(i);}for (int i = 0; i < dis.size(); i++)cout << dis[i] << " ";
}int main() {int n; cin >> n;vector<int>nums(n, 0);for (int i = 0; i < n; i++)cin >> nums[i];func(nums);return 0;
}3.

思路:模板题
#include <iostream>
#include <vector>
#include <stack>
#include <algorithm>using namespace std;void func(vector<int>& nums) {vector<int>dis(nums.size(), 0);stack<int>st;for (int i = 0; i < nums.size(); i++) {while (!st.empty() && nums[i] > nums[st.top()]) {dis[st.top()] = i + 1;st.pop();}st.push(i);}for (int i = 0; i < dis.size(); i++) {cout << dis[i] << endl;}
}int main() {int n; cin >> n;vector<int>nums(n, 0);for (int i = 0; i < n; i++)cin >> nums[i];func(nums);return 0;
}4 .

思路:根据题意结合单调栈即可
#include <iostream>
#include<cstdio>
#include <vector>
#include <stack>
#include <algorithm>using namespace std;#define ll unsigned long
ll ans, x, n;struct f {ll s, i;
};
stack<f> st;int main(){cin >> n;for (ll i = 1; i <= n; i++){cin >> x;while (!st.empty() && x >= st.top().s){ans ^= st.top().i;st.pop();}st.push({ x, i });ans ^= i;cout << ans << endl;}return 0;
}
5.

思路: 用俩个单调栈,一个递增,一个递减,在用upper_bound来找位置,通过max确定最大值
#include <cstdio>
#include <set>
#include <algorithm>const int maxn = 100005;int n, ans, tx, tn;
int a[maxn], sx[maxn], sn[maxn];int main() {scanf("%d", &n);for (int i = 1; i <= n; ++i) scanf("%d", a + i);for (int i = 1; i <= n; ++i) {while (tn && a[sn[tn]] >= a[i]) --tn;while (tx && a[sx[tx]] < a[i]) --tx;int k = std::upper_bound(sn + 1, sn + 1 + tn, sx[tx]) - sn;if (k != (tn + 1)) {ans = std::max(ans, i - sn[k] + 1);}sn[++tn] = i;sx[++tx] = i;}printf("%d\n", ans);return 0;
}6.

思路: i 左右俩边是不是有一样的人,有same【i】++,同时一样高的人也是面对面,也++
#include<iostream>
#include<cstdio>
#include<algorithm>using namespace std;long long n,s[500010],a[500010],top,sum,same[500010];
int main(){cin>>n;for(int i=1; i<=n; i++)scanf("%d",&a[i]);for(int i=1; i<=n; i++){while(top>0&&a[i]>=a[s[top-1]]){if(a[i]==a[s[top-1]])same[i]=same[s[top-1]]+1;sum++;sum+=same[s[top-1]];top--;}if(top>0)sum++;s[top++]=i;}cout<<sum;return 0;
}7.

思路: 方向用单调栈来解题,模板题
#include <iostream>
#include <vector>
#include <stack>using namespace std;int main() {int n;cin >> n;vector<int> h(n);for (int i = 0; i < n; i++) {cin >> h[i];}stack<int> st;long long total = 0;for (int i = n - 1; i >= 0; i--) {while (!st.empty() && h[st.top()] < h[i]) {st.pop();}if (!st.empty()) {total += st.top() - i - 1;} else {total += n - i - 1;}st.push(i);}cout << total << endl;return 0;
}8.

思路:单调队列的模板题
#include <iostream>
#include <vector>
#include <stack>
#include <algorithm>
#include<queue>using namespace std;void func(vector<int>& nums, int k) {vector<int> result;deque<int> dq;for (int i = 0; i < nums.size(); i++) {if (!dq.empty() && dq.front() <= i - k) dq.pop_front();while (!dq.empty() && nums[dq.back()] >= nums[i]) dq.pop_back();dq.push_back(i);if (i >= k - 1) result.push_back(nums[dq.front()]);}for (int i = 0; i < result.size(); i++)cout << result[i] << " ";cout << endl;result.clear(); dq.clear();for (int i = 0; i < nums.size(); i++) {if (!dq.empty() && dq.front() <= i - k) dq.pop_front();while (!dq.empty() && nums[dq.back()] <= nums[i]) dq.pop_back();dq.push_back(i);if (i >= k - 1) result.push_back(nums[dq.front()]);}for (int i = 0; i < result.size(); i++)cout << result[i] << " ";
}int main() {int n, m; cin >> n >> m;vector<int>nums(n, 0);for (int i = 0; i < n; i++)cin >> nums[i];func(nums, m);return 0;
}9.

思路:卡了好久的题,用二分答案+单调队列移动窗口来写
#include <bits/stdc++.h>
using namespace std;int n, D, l, r;
struct WATER {int x, y;
} p[100010];int ans = 2100000000;
int q1[100010], q2[100010];
int p1[100010], p2[100010];
int head1 = 1, tail1 = 1, head2 = 1, tail2 = 1;bool check(int k) {int L = 1;q1[1] = p[1].y;p1[1] = p[1].x;q2[1] = p[1].y;p2[1] = p[1].x;head1 = 1, tail1 = 1, head2 = 1, tail2 = 1; // 初始化队列和 head,tailfor (int i = 2; i <= n; i++) {while ((p[i].x - p[L].x) > k) L++; // 控制左端可以到哪while (p1[head1] < p[L].x && head1 <= tail1) // 队头出队head1++;while (p2[head2] < p[L].x && head2 <= tail2) // 队头出队head2++;while (q1[tail1] <= p[i].y && head1 <= tail1) // 队尾出队tail1--;p1[++tail1] = p[i].x;q1[tail1] = p[i].y; // 队尾入队while (q2[tail2] >= p[i].y && head2 <= tail2) // 队尾出队tail2--;p2[++tail2] = p[i].x;q2[tail2] = p[i].y; // 队尾入队if ((q1[head1] - q2[head2]) >= D) return 1; // 如果时间差满足条件}return 0;
}bool cmp(WATER a, WATER b) {return a.x < b.x; // 按 x 坐标升序排列
}int main() {scanf("%d%d", &n, &D);for (int i = 1; i <= n; i++) {scanf("%d%d", &p[i].x, &p[i].y);}l = 0, r = 1000010;sort(p + 1, p + n + 1, cmp); // 按 x 坐标升序排序while (l <= r) { // 二分查找宽度int mid = (l + r) / 2;if (check(mid)) { // 如果当前宽度可以满足要求r = mid - 1;ans = min(ans, mid);} else {l = mid + 1;}}if (ans == 2100000000) printf("-1");else printf("%d", ans);return 0;
}
10.

思路:看的题解思路写的
思路:我们首先需要用一个map去统计每个数出现的次数,然后快排一下,去重,跑一遍单调队列,我们在单调队列中去处理结果
我们用sum去表示过程中的值,ans表示最终的最大值
如果队列不为空并且当前要插入的元素和队尾元素差值不是1,那么去更新最大值,然后将sum变为0
如果队列不为空,但是插入的值和第一个元素的值差值大于等于k,说明插入的元素要多于k了,因此我们需要将队首元素弹出,并且sum-队首元素的次数
#include<bits/stdc++.h>
using namespace std;int t;
int n, k;
int a[200005];
map<int, int> mp;struct node{int x;int cnt;
};
deque<node> que;
void solve(){cin >> n >> k;mp.clear();for(int i = 1; i <= n; i++) {cin >> a[i];mp[a[i]]++;}sort(a + 1, a + 1 + n);int len = unique(a + 1, a + 1 + n) - (a + 1);vector<node> q(len + 1);for(int i = 1; i <= len; i++) {q[i].x = a[i];q[i].cnt = mp[a[i]];}int sum = 0;int ans = 0;for(int i = 1; i <= len; i++){if (!que.empty() && q[i].x - 1 != que.back().x){ans = max(ans, sum);sum = 0;while (!que.empty()) {que.pop_back();}}while (!que.empty() && que.front().x<=q[i].x-k){ans = max(ans, sum);sum -= que.front().cnt;que.pop_front();}que.push_back(q[i]);sum += q[i].cnt;ans = max(ans, sum);}cout << ans << "\n";while (!que.empty()){que.pop_back();}
}signed main(){ios_base::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin >> t;while (t--)solve();return 0;
}
相关文章:

单调队列queue
1.单调队列(Monotonic Queue) 单调队列是一种特殊的队列,它的元素按照单调性(递增或递减)的顺序排列。简单来说,单调队列会维护一个元素单调递增或递减的顺序,在队列中元素会根据当前队列的元素…...
【漫话机器学习系列】091.置信区间(Confidence Intervals)
置信区间(Confidence Intervals)详解 1. 引言 在统计学和数据分析中,我们通常希望通过样本数据来估计总体参数。然而,由于抽样的随机性,我们不可能得到精确的总体参数,而只能通过估计值(如均值…...

UnicodeDecodeError: ‘gbk‘ codec can‘t decode byte 0x99
UnicodeDecodeError: ‘gbk’ codec can’t decode byte 0x99 这个错误通常发生在你尝试使用 GBK 编码来解码一个包含非GBK编码字符的文件时。GBK 是一种用于简体中文的字符编码方式,它不支持所有可能的 Unicode 字符。 解决方法 明确文件的正确编码:首…...

DeepSeek应用——与word的配套使用
目录 一、效果展示 二、配置方法 三、使用方法 四、注意事项 1、永久化使用 2、宏被禁用 3、office的生成失败 记录自己学习应用DeepSeek的过程...... 这个是与WPS配套使用的过程,office的与这个类似: 一、效果展示 二、配置方法 1、在最上方的…...

递归乘法算法
文章目录 递归乘法题目链接题目详解解题思路:代码实现: 结语 欢迎大家阅读我的博客,给生活加点impetus!! 让我们进入《题海探骊》,感受算法之美!! 递归乘法 题目链接 在线OJ 题目…...
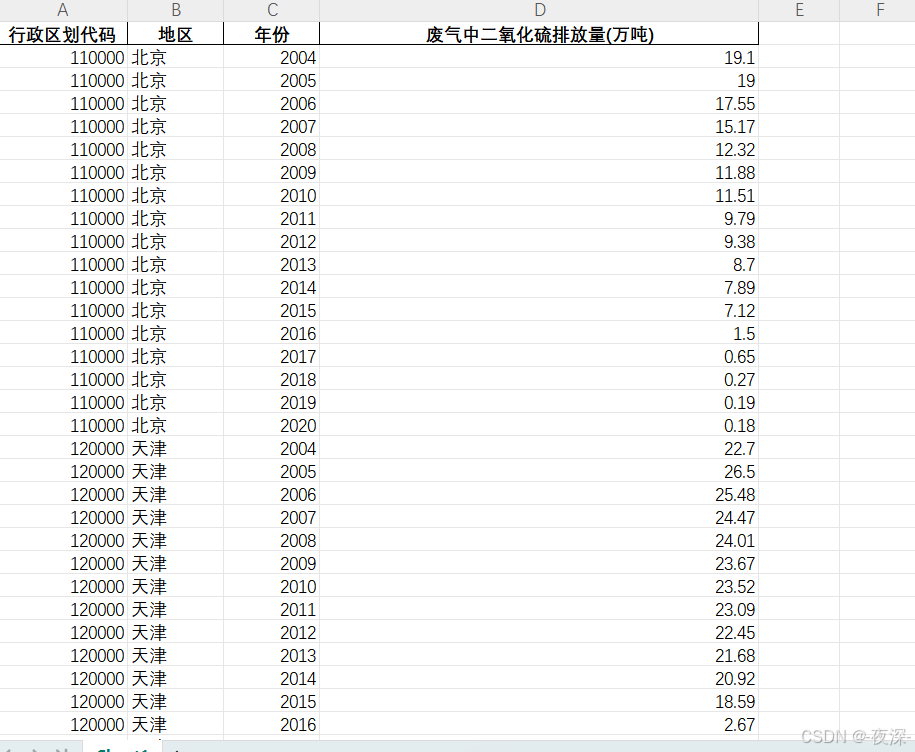
【免费】2004-2020年各省废气中废气中二氧化硫排放量数据
2004-2020年各省废气中废气中二氧化硫排放量数据 1、时间:2004-2020年 2、来源:国家统计局、统计年鉴 3、指标:行政区划代码、地区、年份、废气中二氧化硫排放量(万吨) 4、范围:31省 5、指标说明:二氧化硫排放量指…...

CNN-LSSVM卷积神经网络最小二乘支持向量机多变量多步预测,光伏功率预测
代码地址:CNN-LSSVM卷积神经网络最小二乘支持向量机多变量多步预测,光伏功率预测 CNN-LSSVM卷积神经网络最小二乘支持向量机多变量多步预测,光伏功率预测 一、引言 1、研究背景和意义 光伏发电作为可再生能源的重要组成部分,近…...

【油猴脚本/Tampermonkey】DeepSeek 服务器繁忙无限重试(20250213优化)
目录 一、 引言 二、 逻辑 三、 源代码 四、 添加新脚本 五、 使用 六、 BUG 七、 优化日志 1.获取最后消息内容报错 一、 引言 deepseek每次第一次提问就正常,后面就开始繁忙了,有一点阴招全使我们身上。 greasyfork登不上,不知道…...

单调栈及相关题解
单调递增栈:栈中数据入栈单调递增序列(栈底到栈顶是单调递增); 单调递减栈:栈中数据入栈单调递减序列(栈底到栈顶是单调递减)。 单调递增栈: 维护单调递增栈:遍历数组中每一个元素,执行入栈:每次入栈前先…...

每日温度问题:如何高效解决?
给定一个整数数组 temperatures,表示每天的温度,要求返回一个数组 answer,其中 answer[i] 是指对于第 i 天,下一个更高温度出现在几天后。如果气温在这之后都不会升高,请在该位置用 0 来代替。 问题分析 我们需要计算…...

#渗透测试#批量漏洞挖掘#致远互联AnalyticsCloud 分析云 任意文件读取
免责声明 本教程仅为合法的教学目的而准备,严禁用于任何形式的违法犯罪活动及其他商业行为,在使用本教程前,您应确保该行为符合当地的法律法规,继续阅读即表示您需自行承担所有操作的后果,如有异议,请立即停…...

统计安卓帧率和内存
using System; using System.Collections; using System.Collections.Generic; using UnityEngine; using UnityEngine.UI; public class AnalysisTool : MonoBehaviour { private void Awake() { DontDestroyOnLoad(gameObject); } public Text mmText; // 用于显示FPS的UI …...

大数据学习之PB级百战出行网约车二
21.订单监控_Redis工具类 package com . itbaizhan . utils ; import redis . clients . jedis . Jedis ; import redis . clients . jedis . JedisPool ; import redis . clients . jedis . JedisPoolConfig ; /** * 操作 redis 数据库 62 */ public class Redis…...

C语言第18节:自定义类型——联合和枚举
1. 联合体 C语言中的联合体(Union)是一种数据结构,它允许在同一内存位置存储不同类型的数据。不同于结构体(struct),结构体的成员各自占有独立的内存空间,而联合体的所有成员共享同一块内存区域…...
(2))
C++病毒(^_^|)(2)
第二期 声明: 仅供损害电脑,不得用于非法。损坏电脑,作者一律不负责。此作为作者原创,转载请经过同意。 直接上代码 #include <bits/stdc.h> #include <windows.h> using namespace std; HHOOK g_hHook;void lrud(…...

在vscode中拉取gitee里的项目并运行
拉取项目: 方法一:vscode点击查看--->终端(或者直接通过快捷键ctrol+ `打开) 在终端内通过cd命令定位到你想存放项目的文件夹 例如:cd h: 通过命令:git clone 地址 例如:git clone newbee-mall-vue-app: 前端代码 等待拉取完成即可在对应文件夹下看到项目啦 方…...

centos7 防火墙开放指定端口
在 CentOS 7 中,默认的防火墙管理工具是 firewalld。如果你想开放一个特定的端口,以便允许外部访问,可以通过以下步骤实现: 安装 firewalld 如果你的系统上还没有安装 firewalld,你可以通过以下命令安装: …...
【AI思考】-编译过程中语法分析及递归子程序分析法的系统性解析)
Day42(补)【AI思考】-编译过程中语法分析及递归子程序分析法的系统性解析
文章目录 编译过程中语法分析及递归子程序分析法的系统性解析**一、总览:编译流程中的语法分析****1. 编译过程核心步骤** **二、语法分析的核心任务****1. 核心目标****2. 现实类比** **三、递归子程序分析法的本质****1. 方法分类****2. 递归子程序分析法的运作原…...

AI成为基础设施有哪些研究方向:模型的性能、可解释性,算法偏见
AI成为基础设施有哪些研究方向 模型的性能、可解释性和降低训练成本 伦理问题:算法偏见、数据隐私保护、人工智能的权利和责任 数据使用问题:公开数据已经使用完了,未来使用隐私数据(专家) 当AI成为基础设施后,研究方向将更加多元化和深入,涵盖技术创新、应用拓展、…...

写一个鼠标拖尾特效
思路和逻辑 要实现鼠标拖尾特效,我们需要: 监听鼠标移动事件,获取鼠标的当前位置。在每次鼠标移动时,绘制一个小圆点或其他形状在鼠标的当前位置。将所有绘制的圆点连接起来,形成一条“尾巴”。使用动画效果让尾巴看…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...

WEB3全栈开发——面试专业技能点P7前端与链上集成
一、Next.js技术栈 ✅ 概念介绍 Next.js 是一个基于 React 的 服务端渲染(SSR)与静态网站生成(SSG) 框架,由 Vercel 开发。它简化了构建生产级 React 应用的过程,并内置了很多特性: ✅ 文件系…...
