模糊综合评价法:原理、步骤与MATLAB实现
引言
在复杂决策场景中,评价对象往往涉及多个相互关联的模糊因素。模糊综合评价法通过建立模糊关系矩阵,结合权重分配与合成算子,实现对多因素系统的科学评价。本文详细讲解模糊综合评价法的数学原理、操作步骤,并辅以MATLAB代码实现。
一、模糊综合评价法的数学原理
1.1 基本概念
模糊综合评价基于模糊集合理论,将定性评价转化为定量分析。其核心是通过隶属度函数描述各因素对评价等级的隶属程度,再通过模糊合成运算得到综合评价结果。
设:
- 因素集: U = { u 1 , u 2 , ⋯ , u n } U = \{u_1, u_2, \cdots, u_n\} U={u1,u2,⋯,un}
- 评语集: V = { v 1 , v 2 , ⋯ , v m } V = \{v_1, v_2, \cdots, v_m\} V={v1,v2,⋯,vm}
- 权重向量: A = ( a 1 , a 2 , ⋯ , a n ) A = (a_1, a_2, \cdots, a_n) A=(a1,a2,⋯,an),满足 ∑ i = 1 n a i = 1 \sum_{i=1}^n a_i = 1 ∑i=1nai=1
1.2 模糊关系矩阵
单因素评判矩阵 R R R 表示各因素对评语的隶属度:
R = ( r 11 r 12 ⋯ r 1 m r 21 r 22 ⋯ r 2 m ⋮ ⋮ ⋱ ⋮ r n 1 r n 2 ⋯ r n m ) R = \begin{pmatrix} r_{11} & r_{12} & \cdots & r_{1m} \\ r_{21} & r_{22} & \cdots & r_{2m} \\ \vdots & \vdots & \ddots & \vdots \\ r_{n1} & r_{n2} & \cdots & r_{nm} \end{pmatrix} R= r11r21⋮rn1r12r22⋮rn2⋯⋯⋱⋯r1mr2m⋮rnm
其中 r i j ∈ [ 0 , 1 ] r_{ij} \in [0,1] rij∈[0,1] 表示因素 u i u_i ui 对评语 v j v_j vj 的隶属度。
二、模糊综合评价法的实施步骤
2.1 确定因素集与评语集
因素集需覆盖所有评价指标,例如科研成果评价可选:
U = { 技术水平 , 经济效益 , 社会效益 , 创新性 , 成熟度 } U = \{\text{技术水平}, \text{经济效益}, \text{社会效益}, \text{创新性}, \text{成熟度}\} U={技术水平,经济效益,社会效益,创新性,成熟度}
评语集通常分为5级:
V = { 优秀 , 良好 , 中等 , 合格 , 差 } V = \{\text{优秀}, \text{良好}, \text{中等}, \text{合格}, \text{差}\} V={优秀,良好,中等,合格,差}
2.2 构建模糊关系矩阵
通过专家打分或数据统计确定隶属度。例如10位专家对"技术水平"的评价为:3人评优秀,4人评良好,2人评中等,1人评合格,0人评差,则:
r 1 j = ( 0.3 , 0.4 , 0.2 , 0.1 , 0 ) r_{1j} = (0.3, 0.4, 0.2, 0.1, 0) r1j=(0.3,0.4,0.2,0.1,0)
2.3 确定权重向量
权重反映各因素的重要性,常用方法包括:
- 层次分析法(AHP)
- 熵权法
- 专家打分法
例如某评价权重分配:
A = ( 0.25 , 0.20 , 0.20 , 0.10 , 0.25 ) A = (0.25, 0.20, 0.20, 0.10, 0.25) A=(0.25,0.20,0.20,0.10,0.25)
2.4 选择合成算子
常见的模糊合成算子:
| 算子类型 | 定义 |
|---|---|
| M ( ∧ , ∨ ) M(\wedge, \vee) M(∧,∨) | b j = max 1 ≤ i ≤ n { a i ∧ r i j } b_j = \max\limits_{1 \leq i \leq n} \{a_i \wedge r_{ij}\} bj=1≤i≤nmax{ai∧rij} |
| M ( ⋅ , ∨ ) M(\cdot, \vee) M(⋅,∨) | b j = max 1 ≤ i ≤ n { a i ⋅ r i j } b_j = \max\limits_{1 \leq i \leq n} \{a_i \cdot r_{ij}\} bj=1≤i≤nmax{ai⋅rij} |
| M ( ∧ , ⊕ ) M(\wedge, \oplus) M(∧,⊕) | b j = min ( 1 , ∑ i = 1 n ( a i ∧ r i j ) ) b_j = \min\left(1, \sum_{i=1}^n (a_i \wedge r_{ij})\right) bj=min(1,∑i=1n(ai∧rij)) |
| M ( ⋅ , ⊕ ) M(\cdot, \oplus) M(⋅,⊕) | b j = min ( 1 , ∑ i = 1 n ( a i ⋅ r i j ) ) b_j = \min\left(1, \sum_{i=1}^n (a_i \cdot r_{ij})\right) bj=min(1,∑i=1n(ai⋅rij))(推荐使用) |
2.5 计算综合评价结果
B = A ∘ R = ( b 1 , b 2 , ⋯ , b m ) B = A \circ R = (b_1, b_2, \cdots, b_m) B=A∘R=(b1,b2,⋯,bm)
归一化处理:
B norm = ( b 1 ∑ b i , b 2 ∑ b i , ⋯ , b m ∑ b i ) B_{\text{norm}} = \left( \frac{b_1}{\sum b_i}, \frac{b_2}{\sum b_i}, \cdots, \frac{b_m}{\sum b_i} \right) Bnorm=(∑bib1,∑bib2,⋯,∑bibm)
三、实例分析:科技成果评价
3.1 问题描述
某科研成果从5个指标评价:技术水平、经济效益、社会效益、创新性、成熟度。专家评分矩阵为:
R = ( 0.35 0.39 0.22 0.04 0.17 0.35 0.39 0.09 0 0.30 0.44 0.26 0.09 0.22 0.30 0.39 0.43 0.35 0.22 0 ) R = \begin{pmatrix} 0.35 & 0.39 & 0.22 & 0.04 \\ 0.17 & 0.35 & 0.39 & 0.09 \\ 0 & 0.30 & 0.44 & 0.26 \\ 0.09 & 0.22 & 0.30 & 0.39 \\ 0.43 & 0.35 & 0.22 & 0 \end{pmatrix} R= 0.350.1700.090.430.390.350.300.220.350.220.390.440.300.220.040.090.260.390
权重向量:
A = ( 0.35 , 0.35 , 0.1 , 0.1 , 0.1 ) A = (0.35, 0.35, 0.1, 0.1, 0.1) A=(0.35,0.35,0.1,0.1,0.1)
3.2 计算过程
使用 M ( ⋅ , ⊕ ) M(\cdot, \oplus) M(⋅,⊕) 算子:
-
计算各评语分量
b 1 = 0.35 × 0.35 + 0.35 × 0.17 + 0.1 × 0 + 0.1 × 0.09 + 0.1 × 0.43 = 0.23 b_1 = 0.35 \times 0.35 + 0.35 \times 0.17 + 0.1 \times 0 + 0.1 \times 0.09 + 0.1 \times 0.43 = 0.23 b1=0.35×0.35+0.35×0.17+0.1×0+0.1×0.09+0.1×0.43=0.23
同理得:
B = ( 0.23 , 0.35 , 0.31 , 0.11 ) B = (0.23, 0.35, 0.31, 0.11) B=(0.23,0.35,0.31,0.11) -
归一化处理
B norm = ( 0.23 0.9 , 0.35 0.9 , 0.31 0.9 , 0.11 0.9 ) = ( 0.256 , 0.389 , 0.344 , 0.122 ) B_{\text{norm}} = \left( \frac{0.23}{0.9}, \frac{0.35}{0.9}, \frac{0.31}{0.9}, \frac{0.11}{0.9} \right) = (0.256, 0.389, 0.344, 0.122) Bnorm=(0.90.23,0.90.35,0.90.31,0.90.11)=(0.256,0.389,0.344,0.122) -
结果分析
- 优秀:25.6%
- 良好:38.9%
- 中等:34.4%
- 合格:12.2%
根据最大隶属度原则,该成果应评为良好等级。
四、MATLAB代码实现
4.1 矩阵合成函数
function B = fuzzy_eval(A, R, method)[n, m] = size(R);B = zeros(1, m);for j = 1:mif strcmp(method, 'product_sum')B(j) = sum(A .* R(:,j)');elseif strcmp(method, 'max_min')B(j) = max(min(A, R(:,j)'));endendB = B / sum(B); % 归一化
end
4.2 实例计算
% 输入数据
A = [0.35, 0.35, 0.1, 0.1, 0.1];
R = [0.35 0.39 0.22 0.04;0.17 0.35 0.39 0.09;0 0.30 0.44 0.26;0.09 0.22 0.30 0.39;0.43 0.35 0.22 0];% 计算综合评价
B = fuzzy_eval(A, R, 'product_sum');
disp('综合评价结果:');
disp(B);
4.3 输出结果
综合评价结果:
0.256 0.389 0.344 0.122
五、关键问题讨论
5.1 权重分配敏感性
权重轻微变化可能导致评价结果显著改变。例如将"技术水平"权重从0.35调整为0.4,重新计算:
A_new = [0.4, 0.3, 0.1, 0.1, 0.1];
B_new = fuzzy_eval(A_new, R, 'product_sum');
结果变为:
B new = ( 0.273 , 0.364 , 0.327 , 0.136 ) B_{\text{new}} = (0.273, 0.364, 0.327, 0.136) Bnew=(0.273,0.364,0.327,0.136)
评价结论仍为"良好",但具体分布发生变化。
5.2 算子选择影响
不同合成算子对比:
| 算子类型 | 评价结果 | 结论 |
|---|---|---|
| M ( ∧ , ∨ ) M(\wedge, \vee) M(∧,∨) | (0.35, 0.35, 0.35, 0.1) | 无法分辨 |
| M ( ⋅ , ⊕ ) M(\cdot, \oplus) M(⋅,⊕) | (0.256, 0.389, 0.344, 0.122) | 良好 |
表明 M ( ⋅ , ⊕ ) M(\cdot, \oplus) M(⋅,⊕) 能更好地区分评价等级。
六、扩展应用:多级模糊综合评价
当因素集 U U U 包含子集时,需采用多级评价模型:
- 一级评价:对各子因素集 U i U_i Ui 进行评价,得到 B i = A i ∘ R i B_i = A_i \circ R_i Bi=Ai∘Ri
- 二级评价:将 B i B_i Bi 作为新的因素集,计算 B = A ∘ [ B 1 ; B 2 ; ⋯ ; B s ] B = A \circ [B_1; B_2; \cdots; B_s] B=A∘[B1;B2;⋯;Bs]
6.1 数学模型
B = A ∘ ( A 1 ∘ R 1 A 2 ∘ R 2 ⋮ A s ∘ R s ) B = A \circ \begin{pmatrix} A_1 \circ R_1 \\ A_2 \circ R_2 \\ \vdots \\ A_s \circ R_s \end{pmatrix} B=A∘ A1∘R1A2∘R2⋮As∘Rs
6.2 应用场景
适用于复杂系统的层次化评价,如:
- 企业绩效评估(财务、客户、流程、创新)
- 城市可持续发展评价(经济、环境、社会)
结论
模糊综合评价法通过以下优势成为处理模糊决策问题的有力工具:
- 兼容定性/定量指标
- 灵活应对权重变化
- 支持多层次分析
实际应用中需注意:
- 隶属度函数需通过统计或德尔菲法合理确定
- 定期验证和调整权重分配
- 结合其他方法(如TOPSIS)进行结果验证
相关文章:

模糊综合评价法:原理、步骤与MATLAB实现
引言 在复杂决策场景中,评价对象往往涉及多个相互关联的模糊因素。模糊综合评价法通过建立模糊关系矩阵,结合权重分配与合成算子,实现对多因素系统的科学评价。本文详细讲解模糊综合评价法的数学原理、操作步骤,并辅以MATLAB代码…...
【数据结构-红黑树】
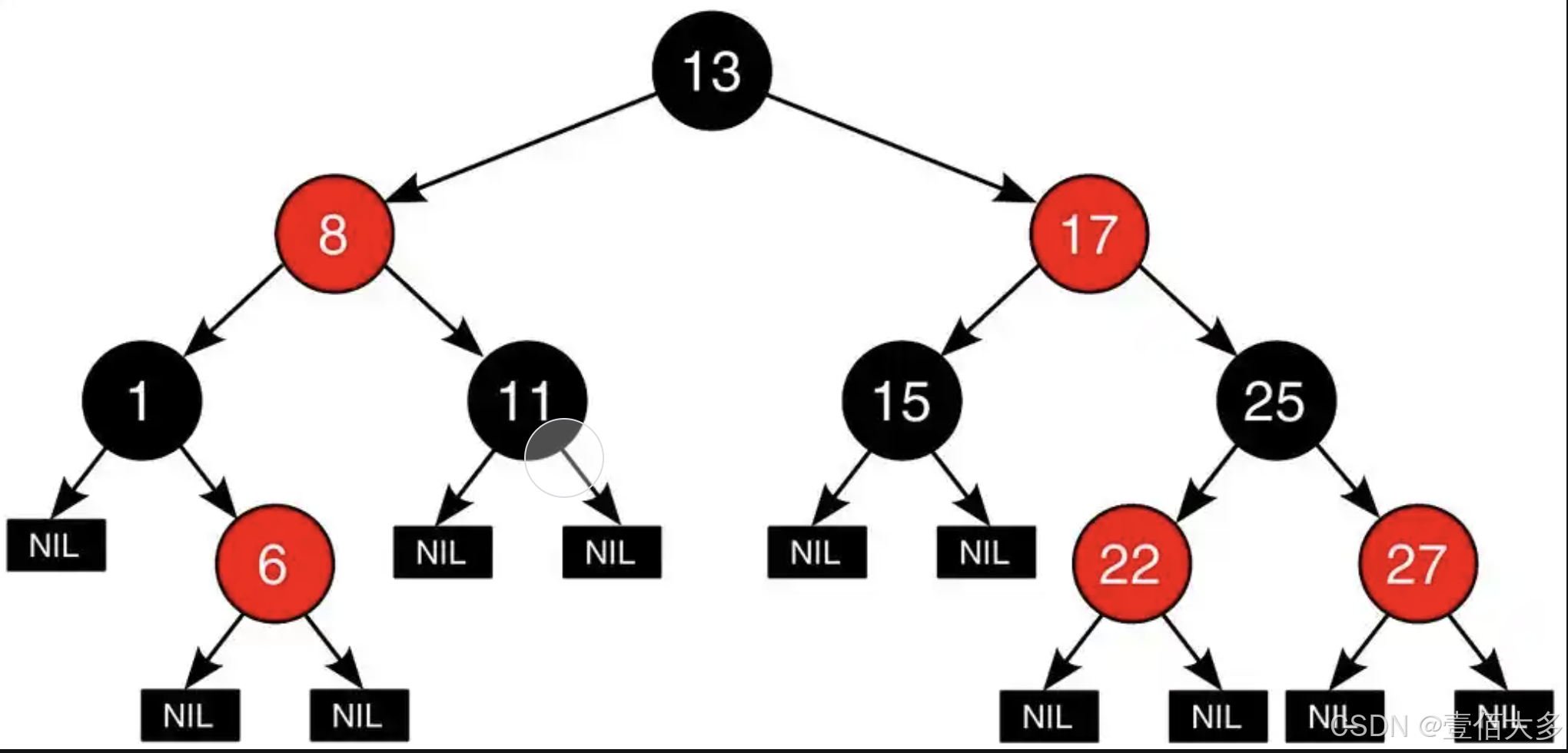
文章目录 红黑树红黑树介绍红黑树的五个基本性质红黑树的平衡原理红黑树的操作红黑树的操作 代码实现节点实现插入和查询操作 红黑树 红黑树介绍 红黑树(Red-Black Tree)是一种自平衡的二叉查找树(Binary Search Tree, BST)&…...

【STM32】舵机SG90
1.舵机原理 舵机内部有一个电位器,当转轴随电机旋转,电位器的电压会发生改变,电压会带动转一定的角度,舵机中的控制板就会电位器输出的电压所代表的角度,与输入的PWM所代表的角度进行比较,从而得出一个旋转…...

【Linux】Socket编程—TCP
🔥 个人主页:大耳朵土土垚 🔥 所属专栏:Linux系统编程 这里将会不定期更新有关Linux的内容,欢迎大家点赞,收藏,评论🥳🥳🎉🎉🎉 文章目…...

c++11 for auto不定参数
数量不定的模板参数。参数分为一个和一包两部分。 冒号的左边声明一个变量。右手边必须是一个容器。从容器(某种数据结构)中找出每一个元素设置到左边这个变量。11之前可以用容器的迭代器去取数据。或者标准库里的foreach...

C#+redis实现消息队列的发布订阅功能
代码 参考c#redis stream实现消息队列以及ack机制文章的思路,实现 SubscribeAttribute.cs using System;namespace DotnetQueue.Attributes {/// <summary>/// 订阅特性/// </summary>[AttributeUsage(AttributeTargets.Method, Inherited false)]pu…...

Docker容器基本操作
容器的基本操作 操作命令(全)命令(简)容器的创建docker container run <image name>docker run <image name>容器的列出(up)docker container lsdocker ps容器的列出(up和exit&…...

从无序到有序:上北智信通过深度数据分析改善会议室资源配置
当前企业普遍面临会议室资源管理难题,预约机制不完善和临时会议多导致资源调度不合理,既有空置又有过度拥挤现象。 针对上述问题,上北智信采用了专业数据分析手段,巧妙融合楼层平面图、环形图、折线图和柱形图等多种可视化工具&a…...

总结:使用JDK原生HttpsURLConnection,封装HttpsUtil工具类,加载自定义证书验证,忽略ssl证书验证
总结:使用JDK原生HttpsURLConnection,封装HttpsUtil工具类,加载自定义证书验证,忽略ssl证书验证 一HttpsUtil工具类二SSLUtil工具类 一HttpsUtil工具类 package com.example.util;import javax.net.ssl.HttpsURLConnection; impo…...

重新定义人机关系边界,Soul以AI社交构建多元社交元宇宙
近年来,AI Native应用的兴起已逐渐成为大众关注的焦点。在此背景下,Soul App的首席技术官陶明在极客公园IF2025创新大会上,发表了一场主题为“人机关系的新边界,Soul如何定义AI社交未来”的演讲。他分享了Soul在人工智能领域内的最新技术进展和战略规划,同时也将Soul社交元宇宙…...
详解)
HTTP 参数污染(HPP)详解
1. 什么是 HTTP 参数污染(HPP)? HTTP 参数污染(HTTP Parameter Pollution,简称 HPP)是一种 Web 应用攻击技术,攻击者通过在 HTTP 请求中注入多个相同的参数来绕过安全控制或篡改应用逻辑&#…...

阿里云轻量服务器docker部署nginx
拉取nginx docker镜像 sudo docker pull nginx创建以下挂载目录及文件 用户目录下:conf html logs conf: conf.d nginx.conf html: index.html conf.d: default.confnginx.conf添加文件内容 events {worker_connections 1024; }http {include /etc/ngi…...
如何从起步阶段开始学习STM32 —— 我应该学习HAL库还是寄存器库?)
(萌新入门)如何从起步阶段开始学习STM32 —— 我应该学习HAL库还是寄存器库?
概念 笔者下面需要介绍的是库寄存器和HAL库两个重要的概念,在各位看完之后,需要决定自己的学习路线到底是学习HAL呢?还是寄存器呢?还是两者都学习呢? 库寄存器 库寄存器就是简单的封装了我们对寄存器的操作…...

Windchill开发-电子仓相关对象信息查询SQL
电子仓相关对象信息查询SQL 一、说明二、数据表信息三、数据表字段说明3.1 HOLDERTOCONTENT3.1.1 对象类型3.1.2 存储类型 3.2 APPLICATIONDATA3.2.1 类别3.2.2 与对象的角色关系3.2.3 存储方式3.2.4 其他字段 3.3 URLDATA3.4 STREAMDATA3.5 FVITEM3.6 FVMOUNT3.6.1 安装状态3.…...

MySQL 数据库定时任务及进阶学习
一、引言 在当今数字化时代,数据管理的高效性和自动化至关重要。MySQL 作为一款广泛应用的开源关系型数据库管理系统,提供了强大的功能来满足各种数据处理需求。其中,定时任务执行功能对于自动化数据操作、维护数据完整性以及优化系统性能具…...

DeepSeek教unity------MessagePack-01
中文:GitCode - 全球开发者的开源社区,开源代码托管平台 MessagePack是C# 的极速 MessagePack 序列化器。它比 MsgPack-Cli 快 10 倍,并且性能超过其他 C# 序列化器。MessagePack for C# 还内置支持 LZ4 压缩——一种极其快速的压缩算法。性能在诸如游戏…...

知识拓展:Python序列化模块 marshal 模块详解
Python marshal 模块学习笔记 1. 简介 marshal 是 Python 的内部序列化格式,主要用于序列化和反序列化 Python 对象。它是 Python 字节码(.pyc文件)使用的序列化格式,比 pickle 更原始和受限,但也更快速和安全。 http…...

leetcode 2684. 矩阵中移动的最大次数
题目如下 数据范围 本题使用常规动态规划就行,不过要注意由于有三个转移的方向,所以我们对dp数组的遍历应该是从上到下 从左到右即按列优先遍历。通过代码 class Solution { public:int maxMoves(vector<vector<int>>& grid) {int …...

机械学习基础-6.更多分类-数据建模与机械智能课程自留
data modeling and machine intelligence - FURTHER CLASSIFICATION 混淆矩阵评估指标:灵敏度和特异度ROC 曲线文字说明部分 AUC:ROC曲线下面积 支持向量机思路补充背景知识点积超平面(HYPERPLANES超平面的法向量到超平面的最小距离数据集与超…...

自动化测试实战
http://8.137.19.140:9090/blog_login.htm 账号: lisi 密码: 123456 上面是系统链接 1. 自动化测试的步骤 1.1 编写Web测试用例 1.2 创建空项目添加依赖 然后我们创建一个新的java项目(使用maven管理),然后引入我们的配置文件:屏幕截图,驱动管理,selenium库 <dependency…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

Python训练营-Day26-函数专题1:函数定义与参数
题目1:计算圆的面积 任务: 编写一个名为 calculate_circle_area 的函数,该函数接收圆的半径 radius 作为参数,并返回圆的面积。圆的面积 π * radius (可以使用 math.pi 作为 π 的值)要求:函数接收一个位置参数 radi…...

Linux安全加固:从攻防视角构建系统免疫
Linux安全加固:从攻防视角构建系统免疫 构建坚不可摧的数字堡垒 引言:攻防对抗的新纪元 在日益复杂的网络威胁环境中,Linux系统安全已从被动防御转向主动免疫。2023年全球网络安全报告显示,高级持续性威胁(APT)攻击同比增长65%,平均入侵停留时间缩短至48小时。本章将从…...
