天童美语:观察你的生活
在孩子的认知里,世界宛如一片充满神秘色彩的未知之境,有着无尽的奥秘等待他们去探索。家长们,引导孩子用心观察世界,领略其中的美妙,这对孩子的成长进程有着极为关键的作用。贵阳天童教育相信:观察生活,感悟生活,会给孩子带来对世界的美好之处的深度体验。
为什么我们建议孩子们去观察生活呢?从认知发展理论来讲,孩子通过观察自然万象,能有效激发他们内在的好奇心与求知欲。
自然环境中的各类元素,无论是宏观的生态系统,还是微观的生物个体,都能成为孩子认识世界的窗口。在观察自然的过程中,孩子能逐步构建起对世界的基本认知框架,锻炼他们的观察力、感知力以及逻辑思维能力。自然的多样性和复杂性,为孩子提供了丰富的学习素材,有助于他们理解事物的发展规律和相互联系。
此外,在社会学习领域,生活中的各种场景和人际交往活动,都是孩子获取知识的重要源泉。通过观察社会生活,孩子能够了解并适应社会规则,掌握人际交往的技巧和原则。在这个过程中,孩子能够从他人的行为模式和互动方式中,学会理解、尊重和关爱他人,从而培养良好的社会情感和道德观念。
而家长作为孩子成长过程中的重要引路人,自身的生活态度和行为方式对孩子有着深远的影响。根据班杜拉的社会学习理论,孩子具有很强的模仿能力,会不自觉地模仿家长的行为。因此,家长若能以积极的态度观察生活、发现美好,孩子也会受到感染,逐渐形成积极乐观的生活态度。
在日常生活中,家长可以引导孩子关注周围环境的各种元素,如建筑的结构特点、城市的布局规划等,激发孩子对空间和结构的认知兴趣。在与孩子进行户外活动时,鼓励孩子观察自然生态系统中的生物关系,同时,家长要积极与孩子互动交流,引导孩子表达自己的观察感受和思考,给予肯定和鼓励,强化孩子观察生活的积极性和主动性。
在这个充满知识和智慧的世界里,孩子将不断汲取成长的养分,茁壮成长。让孩子在观察生活的过程中,不断提升自己的认知水平和社会情感能力,成为一个热爱生活、积极向上、具有探索精神的人。
相关文章:

天童美语:观察你的生活
在孩子的认知里,世界宛如一片充满神秘色彩的未知之境,有着无尽的奥秘等待他们去探索。家长们,引导孩子用心观察世界,领略其中的美妙,这对孩子的成长进程有着极为关键的作用。贵阳天童教育相信:观察生活&…...

网络通信的基石:深入理解 TCP/IP 协议栈与 TCP/UDP 协议
博文题目:网络通信的基石:深入理解 TCP/IP 协议栈与 TCP/UDP 协议 引言 在当今数字化世界中,网络已经渗透到我们生活的方方面面。从浏览网页、收发邮件,到在线视频、远程会议,所有这些便捷的网络应用都离不开一个至关重要的基础设施——TCP/IP 协议栈。它就像是互联网的…...

数据结构-栈和队列的应用
目录 前言一、栈的应用(迷宫问题)1.1 问题描述1.2 算法选择1.3 算法精化1.4 算法实现1.5 问题结果 二、队列的应用(农夫过河问题)2.1 问题描述2.2 算法选择2.3 算法精化2.4 算法实现2.5 问题结果 总结 前言 本篇文章使用两个例子…...

SpringBoot Bug 日志
Spring 循环依赖问题 Bug如下 wxMpConfiguration → subscribeHandler → wxMsgServiceImpl → wxMpConfiguration 解决方案 方案实施方式注意事项接口抽象定义 WxMpService 接口,通过接口注入最佳设计实践 Setter 注入对非必要依赖使用 setter 方法降低耦合度 L…...

halo发布文章的插件问题分析
前言 在准备发文到 halo 系统的时候提示错误如下,全是乱码 尝试将 halo 插件卸载后,再将插件目录下的文件全部删除 插件目录在 C:\Users\Administrator\.vscode\extensions\halo-dev.halo-1.3.0 然后再重新安装插件,在进行初始化的时候依然…...

2.5 模块化迁移策略:从传统项目到模块化系统
模块化迁移策略:从传统项目到模块化系统 将传统 Java 项目迁移至 JDK 9 模块化系统是一项系统性工程,需分阶段实施以降低风险。以下是详细的迁移策略、工具使用和实战示例。 1. 迁移阶段划分 阶段目标关键操作阶段1:兼容性验证确保项目能在…...

java商城解决方案
数字化时代,电子商务已成为企业拓展市场的重要渠道。对于想要建立在线商店的企业来说,选择正确的技术堆栈至关重要。 Java作为一种成熟且广泛使用的编程语言,为构建购物中心提供了强大的功能和灵活性。 商城Java源码:商城开发的核…...

算法-哈希表篇05-四数相加II
四数相加II 力扣题目链接 题目描述 给你四个整数数组 nums1、nums2、nums3 和 nums4 ,数组长度都是 n ,请你计算有多少个元组 (i, j, k, l) 能满足: 0 < i, j, k, l < n nums1[i] nums2[j] nums3[k] nums4[l] 0 解题思路 把数…...

WPS或word接入智能AI
DeepSeek接入WPS 配置WPS (1)下载 OfficeAl助手插件: 插件下载地址:https://www.office-ai.cn/。 安装插件后,打开WPS,菜单栏会新增"OfficeAl助手”选项卡。 如果没有出现, 左上找到文件菜单 -> 选项 ,在…...

Leetcode:学习记录
一、滑动窗口 1. 找出数组中元素和大于给定值的子数组的最小长度 右指针从左到右遍历,在每个右指针下,如果去掉左边元素的元素和大于等于给定值则左指针右移一次,直到小于给定值,右指针右移一个。 2.找到乘积小于给定值的子数组…...
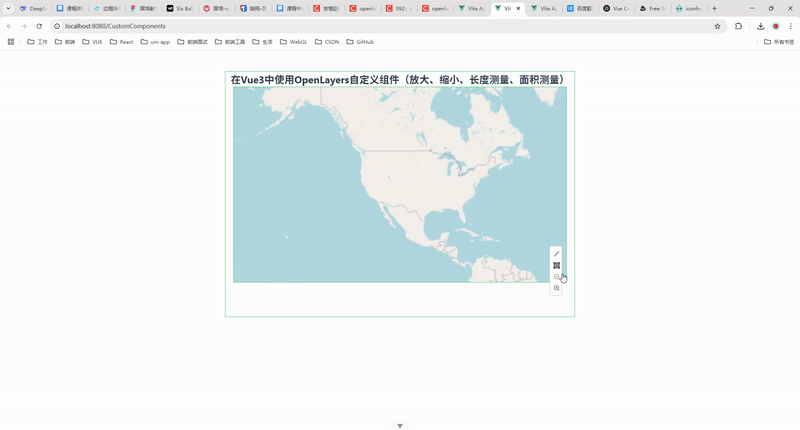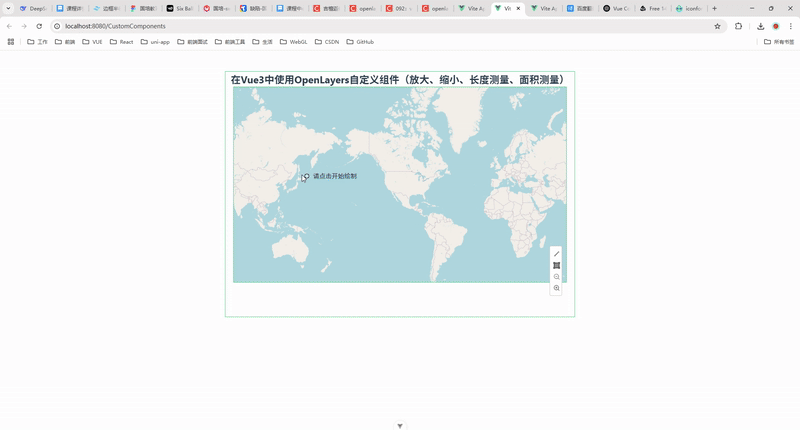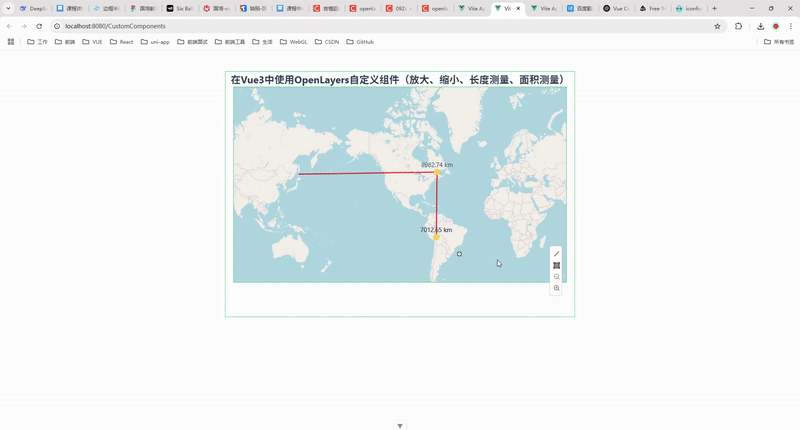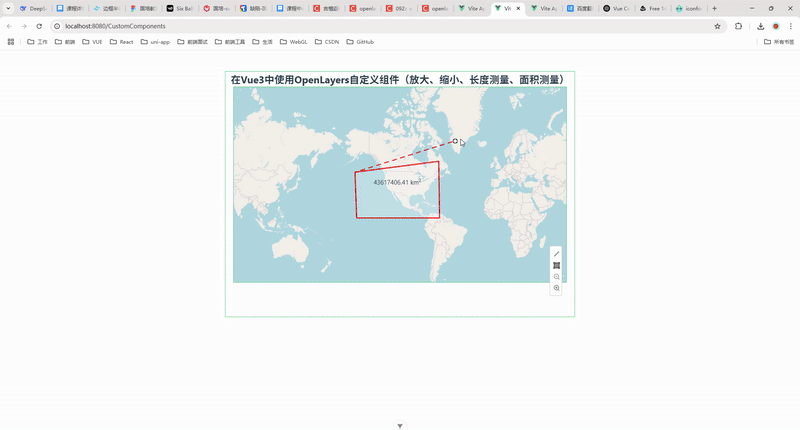
86.在 Vue 3 中使用 OpenLayers 自定义组件(放大、缩小、长度测量、面积测量)
摘要 在 WebGIS 开发中,OpenLayers 是一个非常强大的开源地图库,它可以在 Web 应用中渲染高效的地图。本篇文章将介绍如何在 Vue 3 中使用 OpenLayers,并封装一个自定义地图控件组件,实现地图的放大、缩小、长度测量和面积测量功能…...

http 与 https 的区别?
HTTP(超文本传输协议)和 HTTPS(安全超文本传输协议)是互联网通信的基础协议。随着网络技术的发展和安全需求的提升,HTTPS变得越来越重要。本文将深入探讨HTTP与HTTPS之间的区别,包括其工作原理、安全性、性能、应用场景及未来发展等。 1. HTTP与HTTPS的基本概念 1.1 HT…...

SAIL-RK3576单板运行7b的deepseek对话模型
大概流程: 使用ollama工具进行deepseek的模型部署和使用,先安装ollama工具,在使用ollama工具拉去deepseek模型,最后使用ollama工具加载deepseek模型进行对话...

独立C++ asio库实现的UDP Server
以下是一个使用独立的 C Asio 库实现的 UDP 服务器的示例代码。这个 UDP 服务器可以监听指定端口,接收客户端发送的数据,并将接收到的数据原样返回给客户端。 #include <iostream> #include <asio.hpp> #include <array>class UdpSer…...

SQL Server STUFF 函数的用法及应用场景
在 SQL Server 中,STUFF 函数是一种强大的字符串处理工具,常用于删除指定位置的字符并插入新的字符。通过这个函数,开发者能够灵活地修改字符串,从而在数据处理、字符串拼接和格式化等方面大显身手。本文将深入探讨 STUFF 函数的语…...

MongoDB进阶篇-索引
文章目录 1. 索引概述 2. 索引的类型 2.1 单字段索引 2.2 复合索引 2.3 其他索引 2.3.1 地理空间索引(Geospatial Index) 2.3.2 文本索引(Text Indexes) 2.3.3 哈希索引(Hashed Indexes) 3. 索引相关操作 3.1 查看索引 3.2 创建索引 3.3.1 创建单字段索引 3.3.2 创建复合…...

《机器学习数学基础》补充资料:柯西—施瓦茨不等式以及相关证明
《机器学习数学基础》 153 页,针对图 3-4-3,提出了一个问题:“点 A A A 到 W \mathbb{W} W 上的一个点的距离有无穷多个。现在,我们最关心的是其中最短的那个,怎么找?请参阅 3.6 节。”并且,在…...

VisionPro 划痕检测小练习
划痕检测,我这里用到的是Sobel算子和blob斑点匹配以及blob里面的形态学调整 Sobel 是一种在数字图像处理和计算机视觉领域广泛应用的算法,主要用于边缘检测 脚本展示 #region namespace imports using System; using System.Collections; using System.Drawing; …...

解析 2025 工业边缘计算:三大技术风向的影响力
工业数字化转型的加速,工业边缘计算市场正呈现出蓬勃发展的态势。展望 2025 年,以下三大技术将成为引领工业边缘计算发展的重要风向标。 其一,人工智能与边缘计算的深度融合。人工智能技术将更广泛地应用于工业边缘设备,实现更智…...

企语企业管理系iFair(F23.2_a0)在Debian操作系统中的安装
起因:在安装了F24.8版本后,发现生产用环境和测试、开发用环境还是分开的好。 旧版的用来实验、测试,新版的一步一步小心的配置、使用是比较稳妥的操作。因此,决定在KVM虚拟机上搭建一个F23.2版本的企语系统。 一、 存在的问题 而…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...
