实在智能与宇树科技、云深科技一同获评浙江省“人工智能服务商”、 “数智优品”等荣誉
近日,浙江省经信厅正式公布《2024 年浙江省人工智能应用场景、应用标杆企业、人工智能服务商及 “数智优品” 名单》。 实在智能获评浙江省“人工智能服务商”,核心产品 “实在 Agent 智能体” 入选 “数智优品”。一同获此殊荣的还有宇树科技、云深处科技等行业名企,标志着实在智能在 Agent 智能体赋能企业数字化转型的赛道上,处于领先地位。

此次资质评审工作,是浙江省积极响应国务院关于人工智能赋能新型工业化的战略部署,全面落实推进人工智能赋能新型工业化工作要求的重要举措,旨在通过加快推动人工智能创新应用,深度赋能产业转型升级,加速培育新质生产力。
评审过程严格遵循各单位自主申报、地市推荐、材料初审以及专家评审等规范程序,确保入选的产品或项目在技术创新、实际应用和示范引领等方面具备显著优势,代表了浙江省人工智能领域的顶尖水平。
作为智能化办公及 Agent/RPA 领域的领军企业,实在智能始终致力于通过 AI 技术为企业和政府提供专业的数字员工解决方案,加速企业数字化转型进程。此前,实在智能已荣获中国专利领域最高荣誉“第 25 届国家专利奖”、浙江省“首版次软件产品”等多项殊荣,其研究成果获得国家工信部、科技部以及各地政府和行业媒体的高度认可。

此次入选浙江省 “人工智能服务商” 和 “数智优品” 两项名单,是对实在智能在 “AI 技术实力” 和 “行业服务能力” 的有力背书:
AI技术实力:实在 Agent 智能体作为全球首款兼具 “大脑与手脚” 功能的企业级 AI 智能办公助理,融合了基于垂直行业的千亿级高质量 Tokens 训练的多模态 TARS 大模型,具备卓越的机器学习、逻辑推理及指令生成能力。
基于全球独创的屏幕理解专利技术,实在智能成功攻克了流程自动化领域中通用元素拾取的业界难题,打破了自动化流程对 API 接口的依赖,能够智能识别并操作跨平台的屏幕内容。用户只需通过简单的文本和语音指令,即可自主分解并完成工作任务,真正实现人机协同高效办公。

行业服务能力:实在智能构建了覆盖全球范围的业务及服务网络,在北京、上海、广州、深圳、成都、南京、济南,以及日本东京、马来西亚等地设立了子公司和办事处,确保能够为国内外客户提供无时差、全方位的本地化优质服务。
实在智能产品全面支持国产化信创,与国产芯片、数据库、服务器及操作系统实现深度兼容,“实在数字员工”已在各大央企、国企及政府系统中稳定运行数百万小时。目前,实在智能已成功服务超过 2500 家行业头部客户,业务广泛涵盖金融、制造、运营商、电商、烟草、能源、交通等多个重要领域。

此次荣誉的取得,进一步巩固了实在智能在 Agent 智能体领域的领先优势,也激励着实在智能以更坚定的决心投入到技术创新与服务升级之中。未来,实在智能将继续秉持“AI 赋能商业”的使命,通过前沿的人工智能技术,为企业和组织提供更加高效、智能、创新的解决方案。
相关文章:

实在智能与宇树科技、云深科技一同获评浙江省“人工智能服务商”、 “数智优品”等荣誉
近日,浙江省经信厅正式公布《2024 年浙江省人工智能应用场景、应用标杆企业、人工智能服务商及 “数智优品” 名单》。 实在智能获评浙江省“人工智能服务商”,核心产品 “实在 Agent 智能体” 入选 “数智优品”。一同获此殊荣的还有宇树科技、云深处科…...

SpringAI系列 - RAG篇(三) - ETL
目录 一、引言二、组件说明三、集成示例一、引言 接下来我们介绍ETL框架,该框架对应我们之前提到的阶段1:ETL,主要负责知识的提取和管理。ETL 框架是检索增强生成(RAG)数据处理的核心,其将原始数据源转换为结构化向量并进行存储,确保数据以最佳格式供 AI 模型检索。 …...

Leetcode2080:区间内查询数字的频率
题目描述: 请你设计一个数据结构,它能求出给定子数组内一个给定值的 频率 。 子数组中一个值的 频率 指的是这个子数组中这个值的出现次数。 请你实现 RangeFreqQuery 类: RangeFreqQuery(int[] arr) 用下标从 0 开始的整数数组 arr 构造…...
)
北斗导航 | 周跳探测算法(matlab源码)
===================================================== github:https://github.com/MichaelBeechan CSDN:https://blog.csdn.net/u011344545 ===================================================== 周跳 1. 高次差法2. 相位减伪距法3. TurboEdit算法(MW+GF组合)4. 多项…...

Nginx实战_高性能Web服务器与反向代理的配置全解
1. 引言 1.1 Nginx简介 Nginx(发音为 “engine-x”)是一款轻量级、高性能的HTTP服务器和反向代理服务器。它以其高并发处理能力和低资源消耗而闻名,广泛应用于互联网企业中。Nginx不仅可以作为静态文件服务器,还可以通过反向代理功能与后端应用服务器协同工作。 1.2 Ngi…...

基于微信小程序的电影院订票选座系统的设计与实现,SSM+Vue+毕业论文+开题报告+任务书+指导搭建视频
本系统包含用户、管理员两个角色。 用户角色:注册登录、查看首页电影信息推荐、查看电影详情并进行收藏预定、查看电影资讯、在线客服、管理个人订单等。 管理员角色:登录后台、管理电影类型、管理放映厅信息、管理电影信息、管理用户信息、管理订单等。…...

MySQL智障离谱问题,删了库确还存在、也不能再创建同名库
1、问题 今天跟后端朋友接毕设单子的时候,后端穿过来的【weather.sql】这个文件没弄好,导致这个【weather】数据库的数据是错的,因此我用datagrip的GUI界面直接右键删除,结果就是tmd删不掉,ok,我只能在那新…...

基于单片机的多功能门铃控制系统设计(论文+源码)
1功能设计 本课题为基于单片机的多功能门铃控制系统设计,主要结合单片机技术,门铃控制技术进行设计,在多功能门铃控制系统的设计中,将其主要的设计功能确定如下: (1)可以实现门铃的基础功能…...

分享8款AI生成PPT的工具!含测评
随着人工智能技术的飞速进步,制作PPT变得愈发便捷,仅需输入主题指令,便能在瞬间获得一份完整的演示文稿。尤其在制作篇幅较长的PPT时,手动编写每一页内容并设计格式和排版,不仅效率低下,而且耗时耗力。 本…...

”无痕模式“真的无痕?
无痕模式(也称为 隐身模式): 不保存浏览历史:当你在无痕模式下浏览网页时,浏览器不会保存你的浏览历史。这意味着关闭无痕窗口后,其他人查看浏览器时看不到你访问过的网页记录。 不保存Cookies:…...

蓝桥杯班级活动
题目描述 小明的老师准备组织一次班级活动。班上一共有 n 名 (n 为偶数) 同学,老师想把所有的同学进行分组,每两名同学一组。为了公平,老师给每名同学随机分配了一个 n 以内的正整数作为 id,第 i 名同学的 id 为 ai。 老师希望通…...

PHP支付宝--转账到支付宝账户
官方参考文档: https://opendocs.alipay.com/open/62987723_alipay.fund.trans.uni.transfer?sceneca56bca529e64125a2786703c6192d41&pathHash66064890 可以使用默认应用,也可以自建新应用,此处以默认应用来讲解【默认应用默认支持…...

2.18寒假
今天在题单中看了搜索。 解析:两个一维数组,用于表示上下左右四个方向的偏移量,分别对应 x 轴和 y 轴的偏移,遍历四个方向(左、右、下、上),对于每个方向,检查目标位置是否未走过&am…...
的集成(二))
Docker 与持续集成 / 持续部署(CI/CD)的集成(二)
五、代码示例与解释 (一)Dockerfile 示例 以下是一个简单的基于 Python Flask 应用的 Dockerfile 示例: # 使用Python 3.10-slim作为基础镜像 FROM python:3.10-slim # 设置工作目录 WORKDIR /app # 复制项目文件到容器内的工作目录 C…...
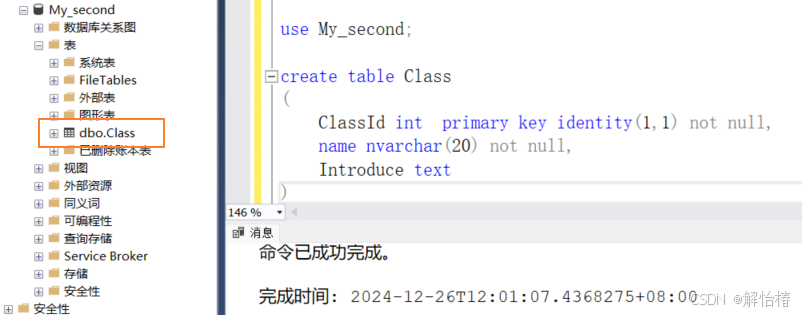
SQL Server的安装和简单使用
目录 一、SQL Server 1.1、简介 1.2、安装包 二、安装SQL Server 2.1、双击安装包 2.2、选择自己想要安装的位置 2.3、点击安装 2.4、安装完成之后会出现以下页面,按照序号依次点击 2.5、不用管密钥,点击下一步 2.6、选择【我接受】 2.7、是否…...
汉诺塔问题)
c/c++蓝桥杯经典编程题100道(19)汉诺塔问题
汉诺塔问题 ->返回c/c蓝桥杯经典编程题100道-目录 目录 汉诺塔问题 一、题型解释 二、例题问题描述 三、C语言实现 解法1:递归法(难度★) 解法2:迭代法(难度★★★) 四、C实现 解法1࿱…...

Linux 信号量
Linux 信号量 一、信号量基础概念1.1 同步机制的核心需求1.2 信号量的核心原理1.3 信号量类型对比 二、实战代码解析2.1 共享内存与信号量结合示例2.2 信号量类实现要点 三、关键实现细节分析3.1 初始化三步骤3.2 SEM_UNDO机制3.3 原子操作保证 四、进阶应用场景4.1 生产者-消费…...

Qt开发①Qt的概念+发展+优点+应用+使用
目录 1. Qt的概念和发展 1.1 Qt的概念 1.2 Qt 的发展史: 1.3 Qt 的版本 2. Qt 的优点和应用 2.1 Qt 的优点: 2.2 Qt 的应用场景 2.3 Qt 的应用案例 3. 搭建 Qt 开发环境 3.1 Qt 的开发工具 3.2 Qt SDK 的下载和安装 3.3 Qt 环境变量配置和使…...

向量库(Vector Database)
向量库 1. 向量库发展史 早期阶段(2000s) 基于关系型数据库的扩展(如 PostgreSQL 的向量插件)。简单相似度计算(如欧氏距离、余弦相似度)。 专用向量库的兴起(2010s) FAISS…...

torchsparse安装过程的问题
1、项目要求torchsparse githttps://github.com/mit-han-lab/torchsparse.gitv1.4.0 2、torch1.8.1cu111 nvcc--version:11.1 这个版本的cuda匹配的gcc、g经常是7.5。设置为7.5. (这个gcc、g版本修改不一定,可以先进行后面的,…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...
