【LeetCode Hot100 矩阵】矩阵置零、螺旋矩阵、旋转图像、搜索二维矩阵II
矩阵
- 1. 矩阵置零(Set Matrix Zeroes)
- 解题思路
- 步骤:
- 代码实现
- 2. 螺旋矩阵(Spiral Matrix)
- 解题思路
- 具体步骤:
- 代码实现
- 3. 旋转矩阵 90 度
- 解决思路
- 代码实现
- 5. 搜索二维矩阵中的目标值
- 解决思路
- 代码实现
1. 矩阵置零(Set Matrix Zeroes)
给定一个 m x n 的矩阵 matrix,如果一个元素是 0,则将其所在的整行和整列都设置为 0。你需要 原地 修改输入矩阵,不能 使用额外的矩阵。
解题思路
要实现原地修改矩阵,可以借助矩阵的第一行和第一列作为辅助存储,记录哪些行和列需要被置零。
步骤:
-
检查第一行和第一列是否包含零:
- 由于我们使用第一行和第一列来标记其他行列是否需要置零,所以需要先检查第一行和第一列是否包含零。如果包含零,我们分别用
rowFlag和colFlag进行标记。
- 由于我们使用第一行和第一列来标记其他行列是否需要置零,所以需要先检查第一行和第一列是否包含零。如果包含零,我们分别用
-
遍历矩阵:
- 从第二行第二列开始遍历整个矩阵。如果某个元素是零,则将其所在的第一行和第一列对应的元素设为零,表示该行和该列后续需要置零。
-
根据标记置零:
- 再次遍历矩阵,根据第一行和第一列的标记,将需要置零的位置修改为零。
-
处理第一行和第一列:
- 最后,根据
rowFlag和colFlag的值,单独处理第一行和第一列的置零问题。
- 最后,根据
代码实现
class Solution {public void setZeroes(int[][] matrix) {int n = matrix[0].length; // 列数int m = matrix.length; // 行数boolean colFlag = false, rowFlag = false;// 检查第一列是否包含零for (int i = 0; i < m; i++) {if (matrix[i][0] == 0) {colFlag = true;break;}}// 检查第一行是否包含零for (int j = 0; j < n; j++) {if (matrix[0][j] == 0) {rowFlag = true;break;}}// 遍历矩阵,使用第一行和第一列标记零的位置for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {if (matrix[i][j] == 0) {matrix[0][j] = 0; // 标记该列matrix[i][0] = 0; // 标记该行}}}// 根据第一行和第一列的标记进行置零for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {if (matrix[0][j] == 0 || matrix[i][0] == 0) {matrix[i][j] = 0;}}}// 处理第一列置零if (colFlag) {for (int i = 0; i < m; i++) {matrix[i][0] = 0;}}// 处理第一行置零if (rowFlag) {for (int j = 0; j < n; j++) {matrix[0][j] = 0;}}}
}
2. 螺旋矩阵(Spiral Matrix)
给定一个 m x n 的矩阵,按螺旋顺序返回矩阵中的所有元素。
解题思路
我们可以模拟螺旋遍历的过程,使用四个边界来控制当前遍历的范围。随着遍历的进行,逐步缩小这些边界,直到遍历完成整个矩阵。
具体步骤:
-
定义边界:
l表示左边界,初始为 0。r表示右边界,初始为m-1。t表示上边界,初始为 0。b表示下边界,初始为n-1。
-
遍历顺序:
- 按照螺旋顺序:从左到右遍历上边界,向下遍历右边界,从右到左遍历下边界,向上遍历左边界。
- 每次遍历完一条边后,更新相应的边界。
-
终止条件:
- 当结果列表的大小等于
m * n时,遍历结束。
- 当结果列表的大小等于
代码实现
class Solution {public List<Integer> spiralOrder(int[][] matrix) {List<Integer> list = new ArrayList<>();int m = matrix[0].length, n = matrix.length;int l = 0, r = m - 1, t = 0, b = n - 1;// 继续遍历直到所有元素都被加入列表while (list.size() < m * n) {// 从左到右遍历上边界for (int i = l; i <= r; i++) {if (list.size() == m * n) break;list.add(matrix[t][i]);}t++; // 缩小上边界的范围// 从上到下遍历右边界for (int i = t; i <= b; i++) {if (list.size() == m * n) break;list.add(matrix[i][r]);}r--; // 缩小右边界的范围// 从右到左遍历下边界for (int i = r; i >= l; i--) {if (list.size() == m * n) break;list.add(matrix[b][i]);}b--; // 缩小下边界的范围// 从下到上遍历左边界for (int i = b; i >= t; i--) {if (list.size() == m * n) break;list.add(matrix[i][l]);}l++; // 缩小左边界的范围}return list;}
}
3. 旋转矩阵 90 度
给定一个 n x n 的二维矩阵,编写一个函数将该矩阵顺时针旋转 90 度。你必须在原地(即不使用额外的二维数组)完成旋转。
解决思路
该问题可以通过两步操作实现:
- 水平翻转:将矩阵上下翻转。
- 对角线翻转:再将矩阵沿主对角线进行翻转。
通过这两步操作,我们可以原地完成矩阵的 90 度顺时针旋转。
代码实现
class Solution {public void rotate(int[][] matrix) {int n = matrix.length;// 先水平翻转for(int i = 0; i < n/2; i++) {for(int j = 0; j < n; j++) {int temp = matrix[i][j];matrix[i][j] = matrix[n-i-1][j];matrix[n-i-1][j] = temp;}}// 再沿着对角线翻转for(int i = 0; i < n; i++) {for(int j = 0; j < i; j++) {int temp = matrix[i][j];matrix[i][j] = matrix[j][i];matrix[j][i] = temp;}}}
}5. 搜索二维矩阵中的目标值
给定一个 m x n 的矩阵 matrix 和一个目标值 target,编写一个函数判断目标值是否在矩阵中。矩阵中的元素按照以下规则排序:
- 每行的元素从左到右升序排列。
- 每列的元素从上到下升序排列。
你需要在 O(m + n) 时间复杂度内完成这个搜索。
解决思路
由于矩阵的元素是按行升序、按列升序排列的,我们可以使用一种特殊的搜索方法:
-
从矩阵的右上角开始搜索:
- 如果当前元素等于目标值,直接返回
true。 - 如果当前元素大于目标值,说明目标值可能在该元素的左边(向左移动一列)。
- 如果当前元素小于目标值,说明目标值可能在该元素的下方(向下移动一行)。
- 如果当前元素等于目标值,直接返回
-
这样,每次搜索都可以排除一行或一列,因此我们可以在
O(m + n)时间复杂度内完成搜索。
代码实现
class Solution {public boolean searchMatrix(int[][] matrix, int target) {int m = matrix.length, n = matrix[0].length;int x = 0, y = n - 1; // 从右上角开始搜索while (x < m && y >= 0) { // 当索引仍在矩阵范围内if (matrix[x][y] == target) {return true; // 找到目标值} else if (matrix[x][y] > target) {y--; // 当前值大于目标值,向左移动} else {x++; // 当前值小于目标值,向下移动}}return false; // 未找到目标值}
}
相关文章:

【LeetCode Hot100 矩阵】矩阵置零、螺旋矩阵、旋转图像、搜索二维矩阵II
矩阵 1. 矩阵置零(Set Matrix Zeroes)解题思路步骤: 代码实现 2. 螺旋矩阵(Spiral Matrix)解题思路具体步骤: 代码实现 3. 旋转矩阵 90 度解决思路代码实现 5. 搜索二维矩阵中的目标值解决思路代码实现 1. …...

【设计模式】【创建型模式】建造者模式(Builder)
👋hi,我不是一名外包公司的员工,也不会偷吃茶水间的零食,我的梦想是能写高端CRUD 🔥 2025本人正在沉淀中… 博客更新速度 👍 欢迎点赞、收藏、关注,跟上我的更新节奏 🎵 当你的天空突…...

如何利用国内镜像从huggingface上下载项目
1、利用镜像快速下载项目 在huggingface上下载模型时速度太慢,可以用下面的方法 pip install -U huggingface_hub pip install huggingface-cliexport HF_ENDPOINThttps://hf-mirror.comhuggingface-cli download --resume-download shenzhi-wang/Llama3-8B-Chine…...

pandas常用操作
pandas是Python中用于数据操作和分析的强大库。以下是一些常用的操作: ### 1. 读取数据 - **从CSV文件读取**: python import pandas as pd df pd.read_csv(path/to/file.csv) - **从Excel文件读取**: python df pd.read_exc…...

linux使用
文章目录 前言操作系统的作用组成二、安装linux系统安装VMware Workstation安装ubuntu图形化,命令行finalshell快照目录理解命令执行命令格式常用命令lscdmkdir 前言 本文讲解认识与使用linux操作系统 操作系统的作用 操作系统是用户和计算机的桥梁。比如我们输入…...

基于豆瓣2025电影数据可视化分析系统的设计与实现
✔️本项目旨在通过对豆瓣电影数据进行综合分析与可视化展示,构建一个基于Python的大数据可视化系统。通过数据爬取收集、清洗、分析豆瓣电影数据,我们提供了一个全面的电影信息平台,为用户提供深入了解电影产业趋势、影片评价与演员表现的工…...

基于Python的深度学习音乐推荐系统(有配套论文)
音乐推荐系统 提供实时音乐推荐功能,根据用户行为和偏好动态调整推荐内容 Python、Django、深度学习、卷积神经网络 、算法 数据库:MySQL 系统包含角色:管理员、用户 管理员功能:用户管理、系统设置、音乐管理、音乐推荐管理、系…...

远程计算机无conda情况下配置python虚拟环境
1. 按照正常流程,根据远程计算机的IP地址/用户名/密码,通过pycharm进行部署 部署流程为: pycharm主菜单--> 工具-->部署 -->配置 **注意,pycharm的远程部署必须是专业版 2. 配置远程python解释器 上图是配置SSH解释器的截图&…...

强化学习-价值学习算法
Sarsa 理论解释 Sarsa是基于时序差分算法的,它的公式非常简单且易理解,不像策略梯度算法那样需要复杂的推导过程。 Sarsa的核心函数是 Q ( s , a ) Q(s, a) Q(s,a),它的含义是在状态 s s s下执行 a a a,在后续轨迹中获取的期望…...

Golang深度学习
前言 在2009年,Google公司发布了一种新的编程语言,名为Go(或称为Golang),旨在提高编程效率、简化并发编程,并提供强大的标准库支持。Go语言的设计者们希望通过Go语言能够解决软件开发中的一些长期存在的问…...
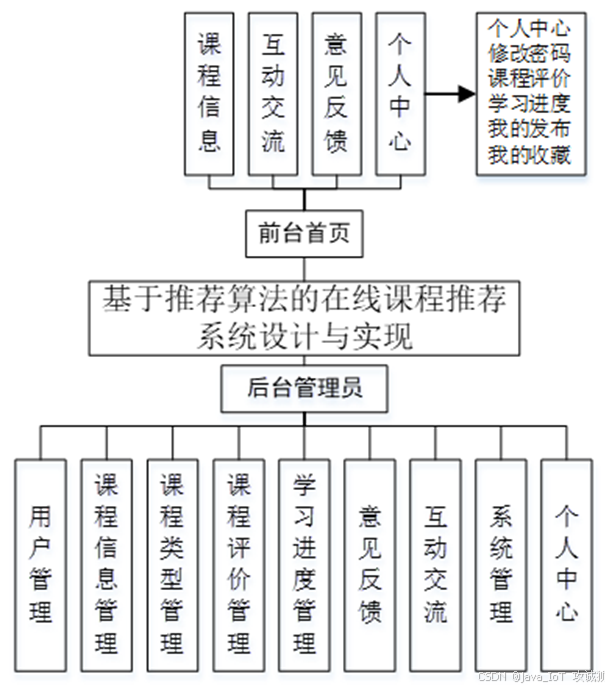
基于推荐算法的在线课程推荐系统设计与实现
开发语言:Java框架:springbootJDK版本:JDK1.8服务器:tomcat7数据库:mysql 5.7(一定要5.7版本)数据库工具:Navicat11开发软件:eclipse/myeclipse/ideaMaven包:…...

es和kibana安装
es安装 安装 wget https://artifacts.elastic.co/downloads/elasticsearch/elasticsearch-8.17.1-linux-x86_64.tar.gz 参考: https://www.cnblogs.com/shamo89/p/18504053 https://blog.csdn.net/u012899618/article/details/130383429 解压 tar -zxvf elastic…...
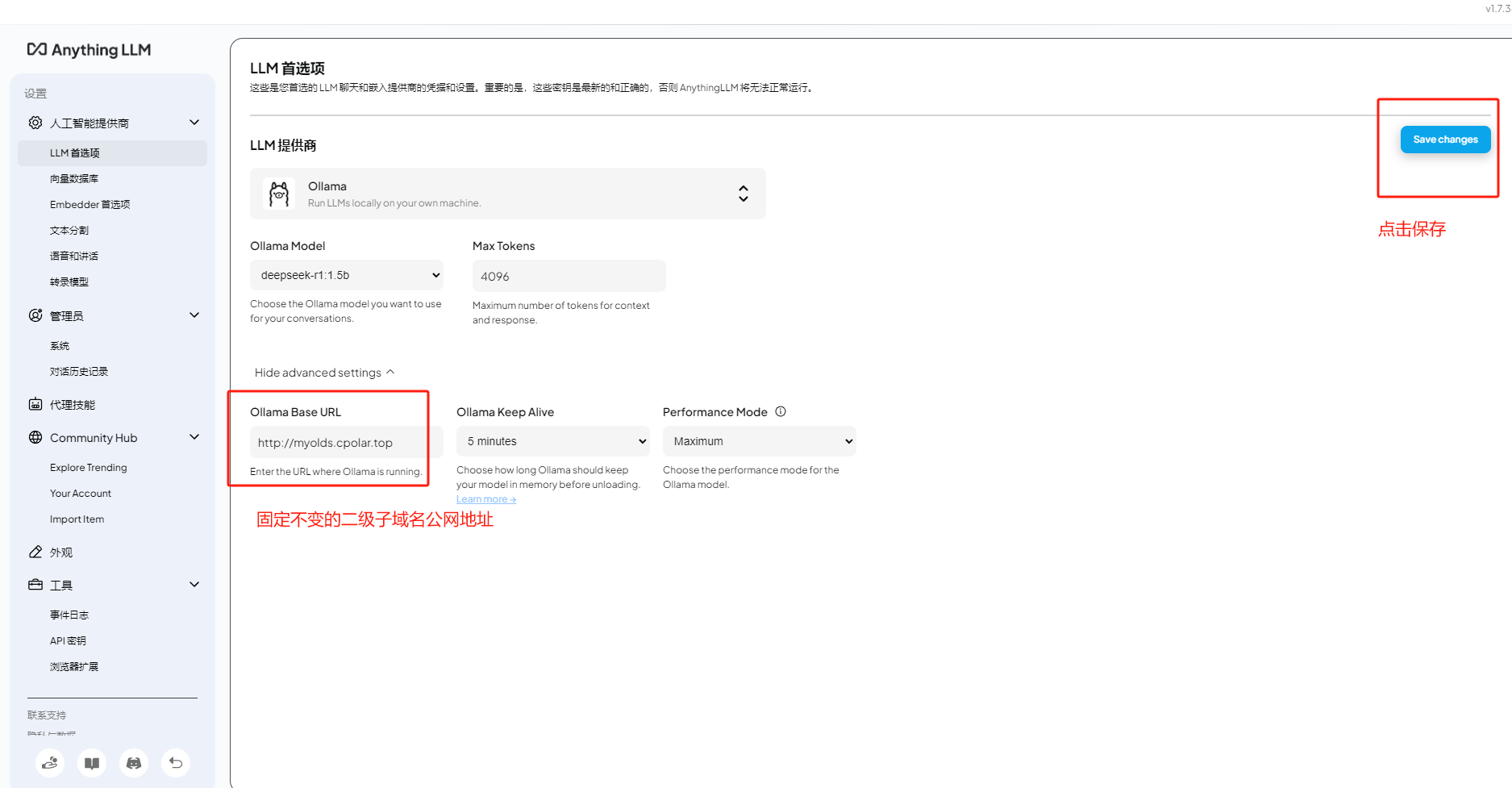
本地部署Anything LLM+Ollama+DeepSeek R1打造AI智能知识库教程
文章目录 前言1. 本地部署OllamaDeepSeek2. 本地安装Anything LLM3. 配置与使用演示4. 远程调用大模型5. 安装内网穿透6. 配置固定公网地址 前言 本文主要介绍如何在Windows电脑上本地部署Ollama并接入DeepSeek R1大模型,然后使用强大的开源AI工具Anything LLM结合…...

zyNo.25
SSRF漏洞 在了解ssrf漏洞前先了解curl命令的使用 1.curl命令的使用 基本格式:curl<参数值>请求地址 get请求:curl http://127.0.0.1 post请求:curl -X POST -d "a1&b2" http://127.0.0.1/(其中,使用-X参…...

Spring框架基本使用(Maven详解)
前言: 当我们创建项目的时候,第一步少不了搭建环境的相关准备工作。 那么如果想让我们的项目做起来方便快捷,应该引入更多的管理工具,帮我们管理。 Maven的出现帮我们大大解决了管理的难题!! Maven…...

关于前后端分离跨域问题——使用DeepSeek分析查错
我前端使用ant design vue pro框架,后端使用kratos框架开发。因为之前也解决过跨域问题,正常是在后端的http请求中加入中间件,设置跨域需要通过的字段即可,代码如下所示: func NewHTTPServer(c *conf.Server, s *conf…...
三层渗透测试-DMZ区域 二三层设备区域
DMZ区域渗透 信息收集 首先先进行信息收集,这里我们可以选择多种的信息收集方式,例如nmap如此之类的,我的建议是,可以通过自己现有的手里小工具,例如无影,密探这种工具,进行一个信息收集。以免…...

领航Linux UDP:构建高效网络新纪元
欢迎来到 破晓的历程的 博客 ⛺️不负时光,不负己✈️ 文章目录 引言Udp和Tcp的异同相同点不同点总结 1.1、socket1.2、bind1.3、recvfrom1.4、sendto2.1、代码2.1、说明3.1、代码3.2、说明 引言 在前几篇博客中,我们学习了Linux网络编程中的一些概念。…...

基于MATLAB的均匀面阵MUSIC算法DOA估计仿真
基于MATLAB的均匀面阵MUSIC算法DOA估计仿真 文章目录 前言一、二维MUSIC算法原理二、二维MUSIC算法MATLAB仿真三、MATLAB源代码总结 前言 \;\;\;\;\; 在波达角估计算法中,MUSIC 算法与ESPRIT算法属于特征结构子空间算法,是波达角估计算法中的基石。在前面…...

HTML/CSS中后代选择器
1.作用:选中指定元素中,符合要求的后代元素. 2.语法:选择器1 选择器2 选择器3 ...... 选择器n(使用空格隔开) 3.举例: /* 选中ul中的所有li */ul li{color: red;}/* 选中类名为subject元素中的所有li */.subject li{color: blue;}/* 选中类名为subject元素中的所有类名为f…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表
设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...

c++第七天 继承与派生2
这一篇文章主要内容是 派生类构造函数与析构函数 在派生类中重写基类成员 以及多继承 第一部分:派生类构造函数与析构函数 当创建一个派生类对象时,基类成员是如何初始化的? 1.当派生类对象创建的时候,基类成员的初始化顺序 …...
