【R语言】非参数检验
一、Mann-Whitney检验
在R语言中,Mann-Whitney U检验(也称为Wilcoxon秩和检验)用于比较两个独立样本的中位数是否存在显著差异。它是一种非参数检验,适用于数据不满足正态分布假设的情况。
1、独立样本
# 创建两个独立样本数据
group1 <- c(5, 6, 7, 8, 9)
group2 <- c(3, 4, 5, 6, 7, 8)# 执行Mann-Whitney U检验
result <- wilcox.test(group1, group2)
result
W = 22:是Wilcoxon秩和检验的统计量W的值。这个值反映了两个样本在秩次上的相对位置。
p-value = 0.231:检验的p值。p值用于判断结果的显著性。p值为0.231,大于常用的显著性水平0.05,因此不能拒绝零假设。
alternative hypothesis:true location shift is not equal to 0:表明备择假设是两个样本的中位数(或位置参数)之间存在显著差异。由于p值大于0.05,我们没有足够的证据支持备择假设,即不能认为两个样本的中位数之间存在显著差异。
2、非独立样本
当两组数据室非独立样本,且不满足非独立样本t检验时,也可使用wilcox.test()函数,但需要令参数paired=TRUE,这样它将执行Wilcon秩和检验。
# 用安眠药对增加睡眠时长效果做例子
head(sleep)
wilcox.test(extra ~ group, data=sleep, paired=TRUE, alternative="less")
p-value = 0.004545:检验的p值。p值非常小,远小于常用的显著性水平0.05,表明观察到的数据差异在统计上是显著的。
alternative hypothesis: true location shift is less than 0:表明备择假设是两个配对样本的中位数差异(或位置参数的差异)小于0。这意味着假设在配对组中,第二个测量值通常小于第一个测量值。
二、Kruskal-Waillis检验
在R语言中,Kruskal-Wallis检验是一种非参数检验方法,用于比较三个或更多独立样本的中位数是否存在显著差异。这个检验是Mann-Whitney U检验在多组样本情况下的扩展,不假设数据服从正态分布。
# 设置随机种子以确保结果可重复
set.seed(123456)
# 创建三个分组变量,每组20个观测值
group <- factor(rep(c("A", "B", "C"), each = 20))
# 创建响应变量,每个组的均值不同
values <- c(rnorm(20, mean = 5), rnorm(20, mean = 6), rnorm(20, mean = 7)) # 执行Kruskal-Wallis检验
result <- kruskal.test(values ~ group)
result
df:自由度,通常是组数减1。
p-value:用于判断结果的显著性。如果p值小于显著性水平(如0.05),则拒绝零假设,认为至少有两个组的中位数存在显著差异。
alternative:备择假设的类型(通常是双侧的,即任何组之间的中位数差异都不为零)。
相关文章:

【R语言】非参数检验
一、Mann-Whitney检验 在R语言中,Mann-Whitney U检验(也称为Wilcoxon秩和检验)用于比较两个独立样本的中位数是否存在显著差异。它是一种非参数检验,适用于数据不满足正态分布假设的情况。 1、独立样本 # 创建两个独立样本数据…...

【力扣Hot 100】栈
1. 有效的括号 给定一个只包括 (,),{,},[,] 的字符串 s ,判断字符串是否有效。 有效字符串需满足: 左括号必须用相同类型的右括号闭合。左括号必须以正确的顺序闭合。每个右括号都有一个对应…...

HTTP 与 HTTPS:协议详解与对比
文章目录 概要 一. HTTP 协议 1.1 概述 1.2 工作原理 1.3 请求方法 1.4 状态码 二. HTTPS 协议 2.1 概述 2.2 工作原理 2.3 SSL/TLS 协议 2.4 证书 三. HTTP 与 HTTPS 的区别 四. 应用场景 4.1 HTTP 的应用场景 4.2 HTTPS 的应用场景 概要 HTTP(Hy…...

C++编程语言:抽象机制:模板和层级结构(Bjarne Stroustrup)
目录 27.1 引言(Introduction) 27.2 参数化和层级结构(Parameterization and Hierarchy) 27.2.1 生成类型(Generated Types) 27.2.2 模板转换(Template Conversions) 27.3 类模板层级结构(Hierarchies of Class Templates) 27.3.1 模板对比接口(Templates as Interf…...

建筑兔零基础自学python记录22|实战人脸识别项目——视频人脸识别(下)11
这次我们继续解读代码,我们主要来看下面两个部分; 至于人脸识别成功的要点我们在最后总结~ 具体代码学习: #定义人脸名称 def name():#预学习照片存放位置path M:/python/workspace/PythonProject/face/imagePaths[os.path.join(path,f) f…...

在使用export default 导出时,使用的components属性的作用?
文章目录 析与思考回答 析与思考 在 Vue.js 中,使用 export default 导出组件时,通常会通过 components 选项将子组件也导出出来(其实是将子组件进行局部注册) 。这涉及到 Vue.js 组件的注册机制。为了更清晰地理解这个问题&…...
)
以太网交换基础(涵盖二层转发原理和MAC表的学习)
在当今的网络世界中,以太网交换技术是局域网(LAN)的核心组成部分。无论是企业网络、学校网络还是家庭网络,以太网交换机都扮演着至关重要的角色。本文将详细介绍以太网交换的基础知识,包括以太网协议、帧格式、MAC地址…...

Vue 实现通过URL浏览器本地下载 PDF 和 图片
1、代码实现如下: 根据自己场景判断 PDF 和 图片,下载功能可按下面代码逻辑执行 const downloadFile async (item: any) > {try {let blobUrl: any;// PDF本地下载if (item.format pdf) {const response await fetch(item.url); // URL传递进入i…...

【2025最新计算机毕业设计】基于SpringBoot+Vue非遗传承与保护研究系统【提供源码+答辩PPT+文档+项目部署】
作者简介:✌CSDN新星计划导师、Java领域优质创作者、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和学生毕业项目实战,高校老师/讲师/同行前辈交流。✌ 主要内容:🌟Java项目、Python项目、前端项目、PHP、ASP.NET、人工智能…...

组合总和力扣--39
目录 题目 思路 剪枝优化 代码 题目 给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。 candidates 中的…...
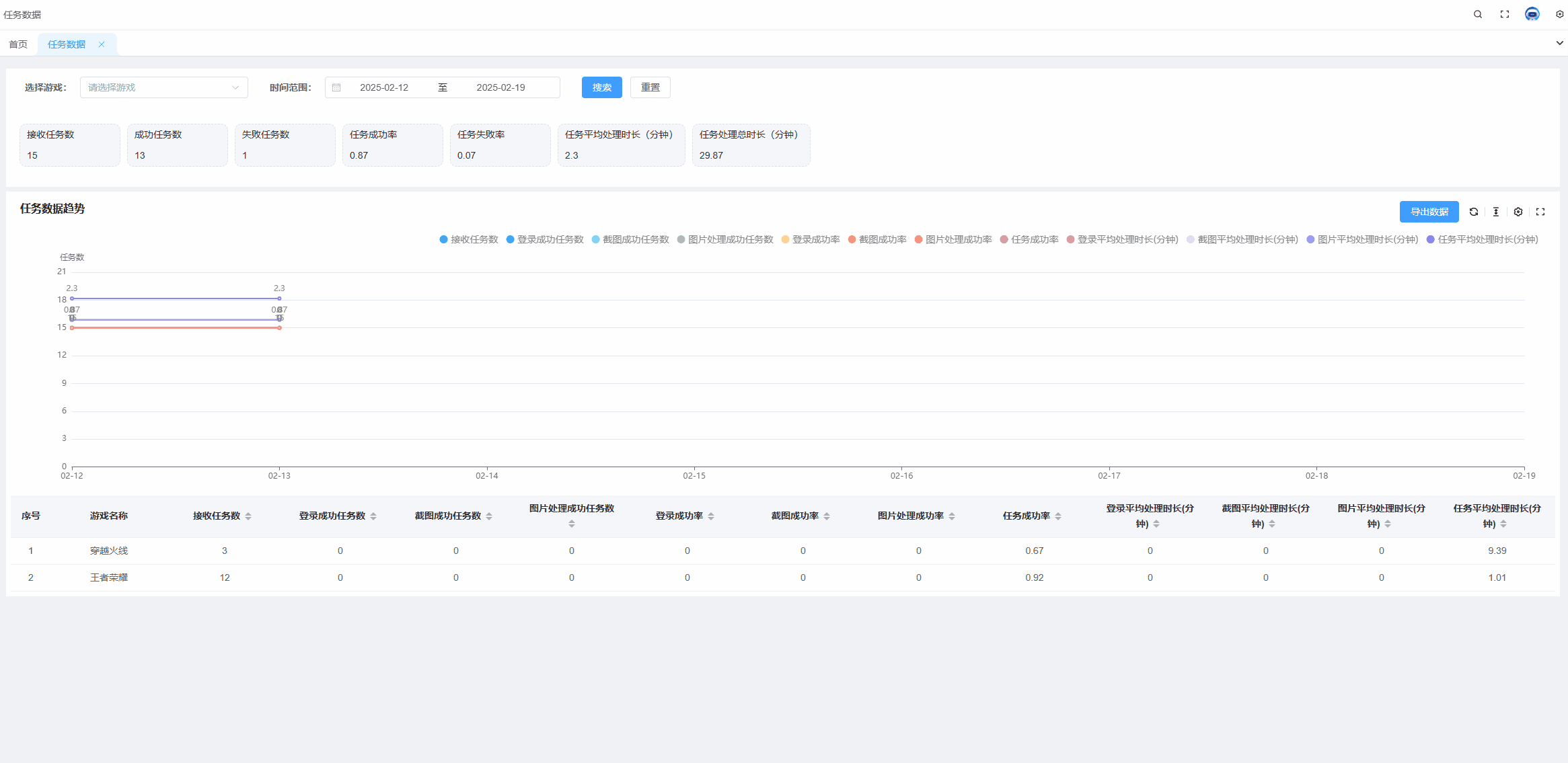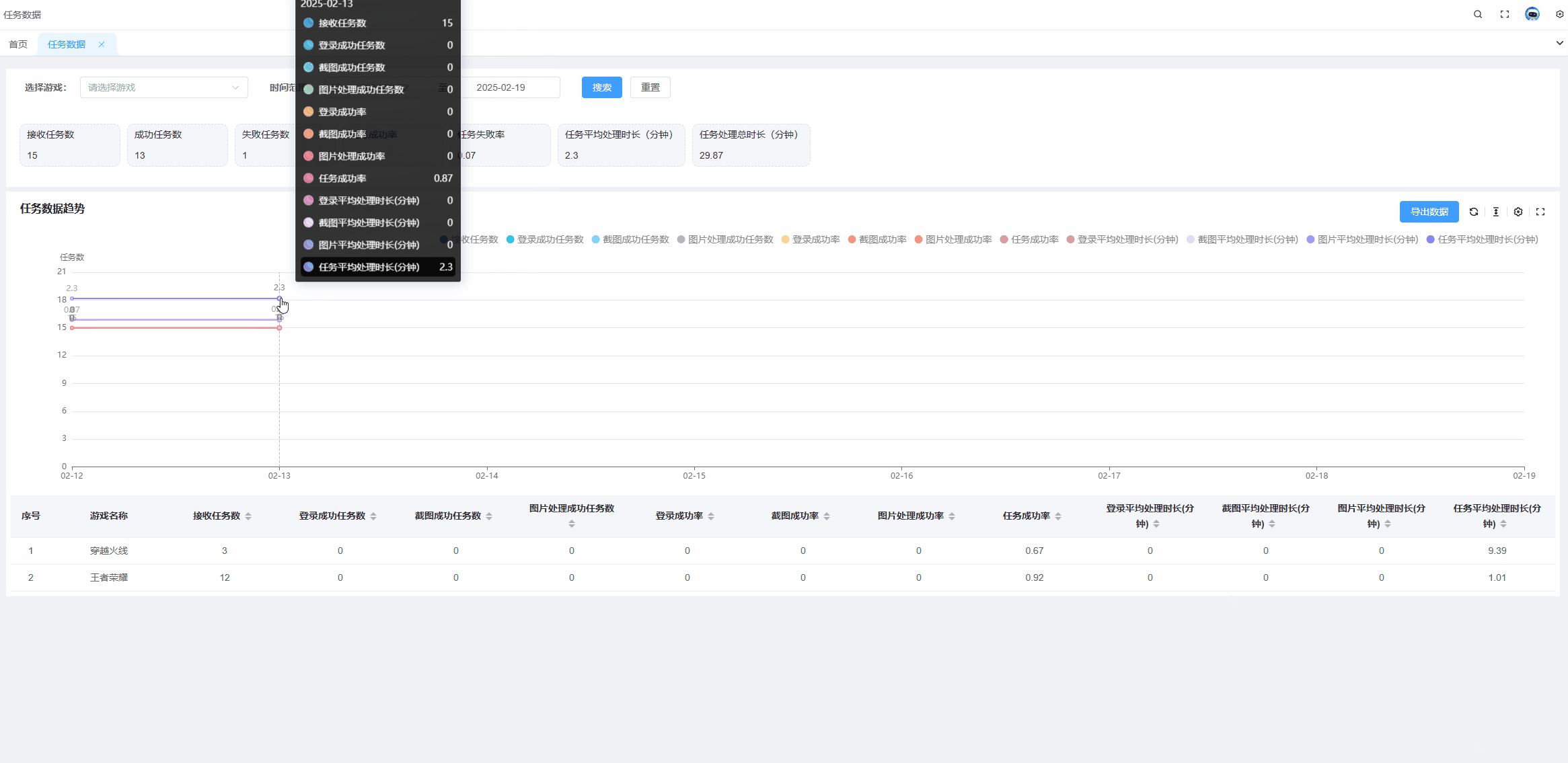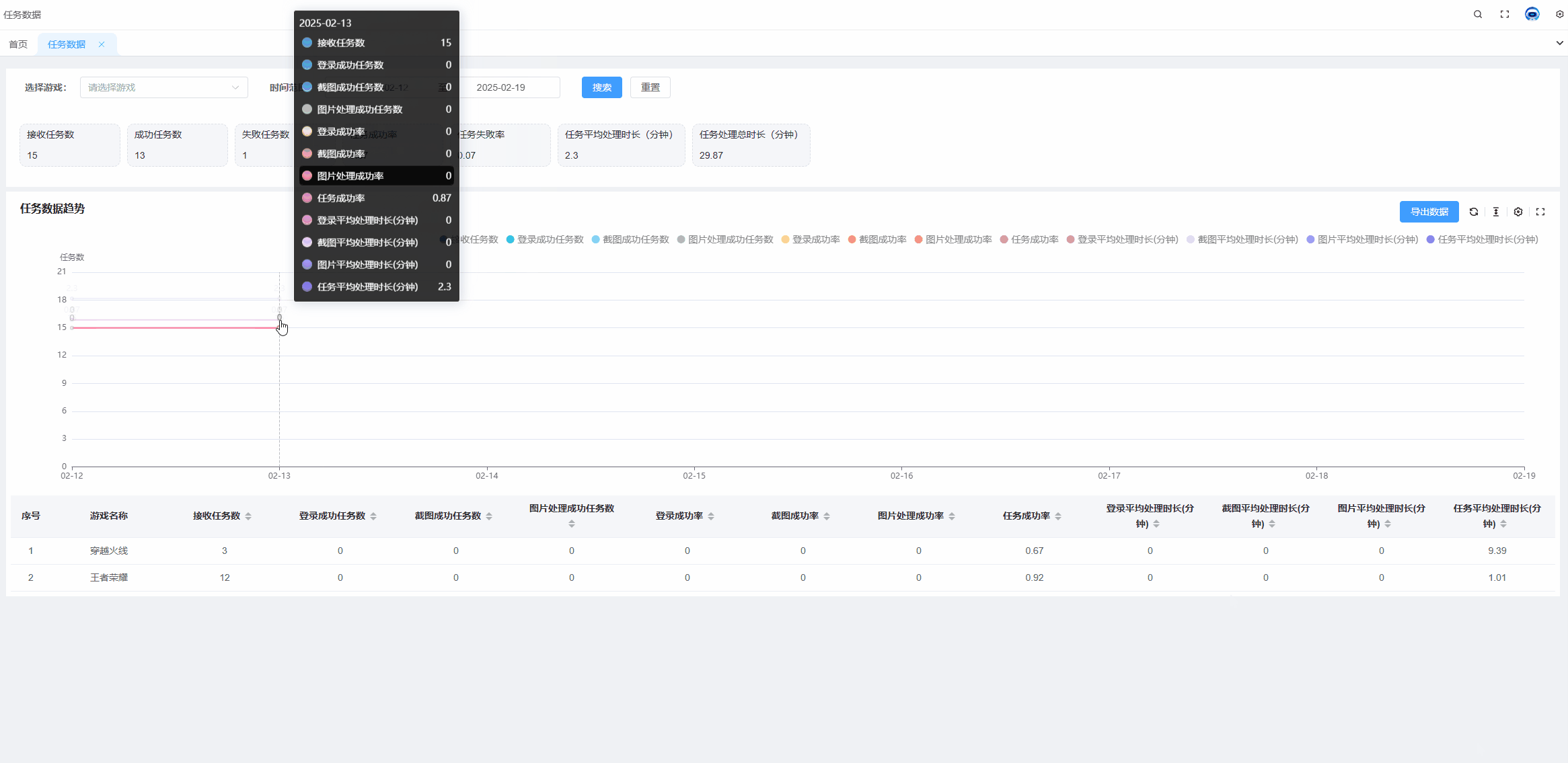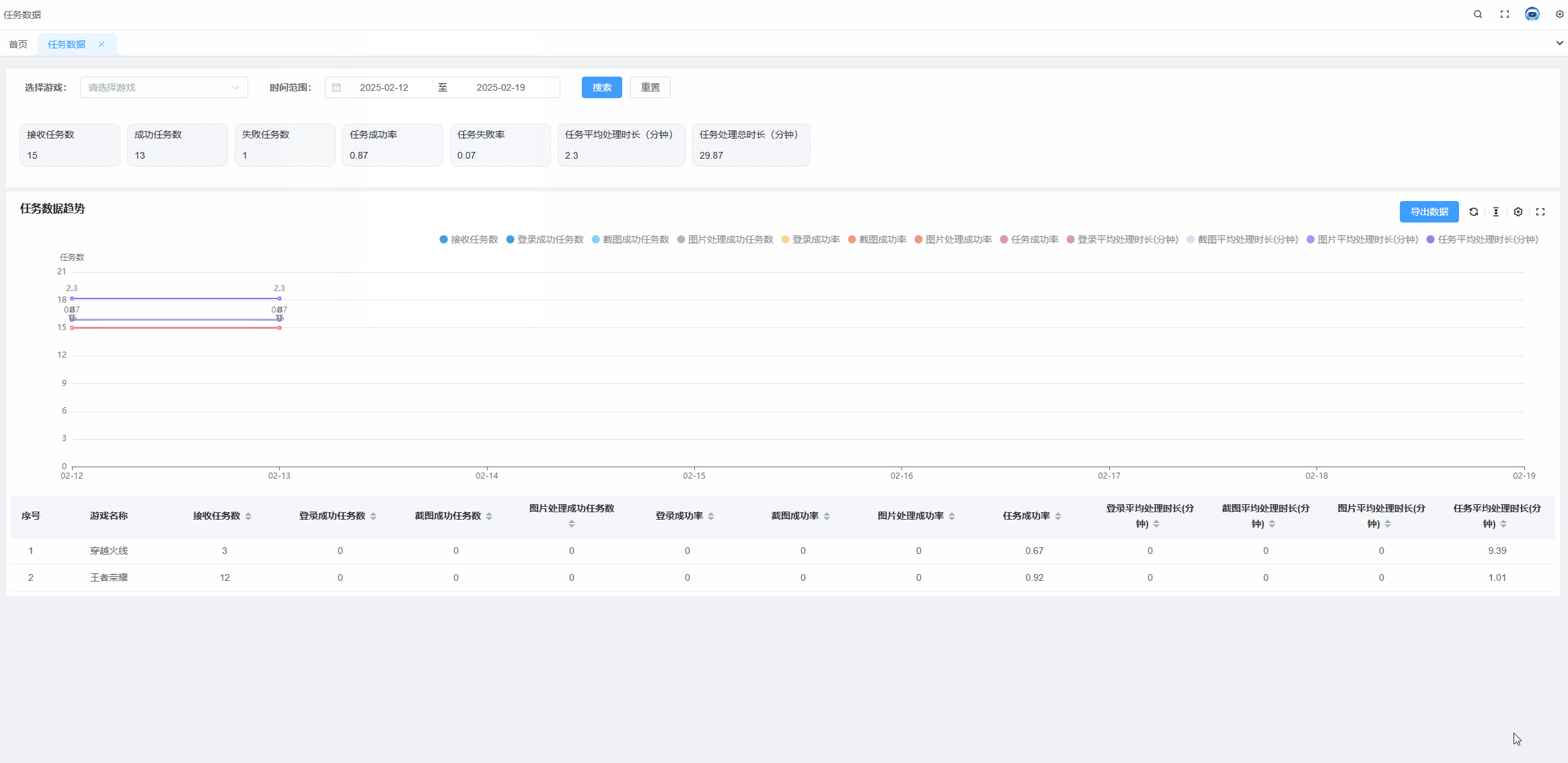
echarts tooltip高亮某个值,某一项选中高亮状态
需求: 当有多组数据的时候,常常需要对比同一x轴的不同线上的点的数据,并且当数据组过多的时候,也就是线过多的时候,需要明确知道我们当前选中的线是哪条。 解决方案: 通过设置显示x轴的tooltip可以显示同…...

Vue 3:基于按钮切换动态图片展示(附Demo)
目录 前言1. Demo2. 升级Demo3. 终极Demo 前言 原先写过类似的知识点: 详细分析el-breadcrumb 面包屑的基本知识(附Demo)详细分析el-card中的基本知识(附Demo) 本篇博客将介绍如何通过点击按钮切换不同的图片&#…...

【Java】泛型与集合篇 —— 泛型
目录 泛型泛型的核心作用泛型类型(类)定义与使用类型参数命名约定泛型方法定义与调用与泛型类的区别通配符上界通配符下界通配符有界类型参数类型擦除类型擦除过程影响好处泛型 泛型的核心作用 泛型是 Java 实现代码复用和类型安全的重要机制。它允许在类、接口和方法中定义…...

【JAVA:list中再定义一个list对象,循环赋值不同的list数据,出现追加重复数据问题】
问题描述: list中再定义一个list对象,循环赋值不同的list数据,结果全部都累加到每条数据中了,每条数据中都出现重复数据。 问题解决: 1.创建树结构方法信息 2.创建一个新的 List 对象,避免引用问题 3.使…...

为什么外贸办公需要跨境专线网络?
你好,今天我们来聊聊SD-WAN技术在出海企业办公中的应用以及其带来的诸多优势。当今出海企业在与海外分支机构或合作伙伴开展高效的网络通讯和数据传输时,面临着许多挑战。此时,SD-WAN作为一种新兴的网络优化技术,正在改变这些企业…...

帆软报表FineReport入门:简单报表制作[扩展|左父格|上父格]
FineReport帮助文档 - 全面的报表使用教程和学习资料 数据库连接 点击号>>JDBC 选择要连接的数据库>>填写信息>>点击测试连接 数据库SQLite是帆软的内置数据库, 里面有练习数据 选择此数据库后,点击测试连接即可 数据库查询 方法一: 在左下角的模板数据集…...

Nginx 在Linux中安装、使用
Nginx 在Linux中安装、使用 一、官网下载Nginx 官网地址:http://nginx.org/en/download.html 二、上传到服务器解压 1、上传到指定的服务器地址 上传的地址自己决定,我上传到 /data/home/prod/nginx/ 2、解压 使用命令: tar -zxvf “你的N…...

在Vue项目中使用three.js在前端页面展示PLY文件或STL文件
前言:这是一个3d打印局域网管理系统的需求 一、安装three.js three.js官网:https://threejs.org/docs/#manual/en/introduction/Installation 我用的是yarn,官网用的是npm 二、使用three.js 1.在script部分导入three.js import * as THREE from thr…...

DeepSeek笔记(二):DeepSeek局域网访问
如果有多台电脑,可以通过远程访问,实现在局域网环境下多台电脑共享使用DeepSeek模型。在本笔记中,首先介绍设置局域网多台电脑访问DeepSeek-R1模型。 一、启动Ollama局域网访问 1.配置环境变量 此处本人的操作系统是Windows11,…...

【LeetCode Hot100 矩阵】矩阵置零、螺旋矩阵、旋转图像、搜索二维矩阵II
矩阵 1. 矩阵置零(Set Matrix Zeroes)解题思路步骤: 代码实现 2. 螺旋矩阵(Spiral Matrix)解题思路具体步骤: 代码实现 3. 旋转矩阵 90 度解决思路代码实现 5. 搜索二维矩阵中的目标值解决思路代码实现 1. …...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...
