蓝桥杯 Java B 组之背包问题、最长递增子序列(LIS)
Day 4:背包问题、最长递增子序列(LIS)
📖 一、动态规划(Dynamic Programming)简介
动态规划是一种通过将复杂问题分解成更小的子问题来解决问题的算法设计思想。它主要用于解决具有最优子结构和重叠子问题的问题。
- 最优子结构:问题的最优解可以通过子问题的最优解组合得到。
- 重叠子问题:子问题的解可以在多次计算中复用,避免了重复计算。
在使用动态规划时,通常会构造一个“状态转移方程”,该方程描述了如何通过子问题的解来得到当前问题的解。
📖 二、背包问题
01背包问题(0/1 Knapsack)
问题描述: 给定一个背包和若干个物品,每个物品有一个重量和价值。求背包能够承载的最大价值。
- 背包容量:
W。 - 物品数目:
n。 - 每个物品的重量和价值分别为
w[i]和v[i]。 - 我们需要选择一些物品放入背包,使得背包的总价值最大。
思路与分析:
- 状态定义:
- 定义
dp[i][w]为前i个物品中,放入背包容量为w时能够达到的最大价值。
- 定义
- 状态转移:
- 如果不选择第
i个物品:dp[i][w] = dp[i-1][w]。 - 如果选择第
i个物品:dp[i][w] = dp[i-1][w - weight[i]] + value[i],前提是w >= weight[i]。
- 如果不选择第
- 最终的答案为
dp[n][W]。
代码实现(01背包问题):
public class Knapsack {public int knapsack(int W, int[] weights, int[] values, int n) {// dp[i][w]表示前i个物品,背包容量为w时的最大价值int[][] dp = new int[n + 1][W + 1];// 填表,i表示物品数量,w表示背包容量for (int i = 1; i <= n; i++) {for (int w = 1; w <= W; w++) {// 不选择第i个物品dp[i][w] = dp[i - 1][w];// 选择第i个物品,前提是背包容量足够if (w >= weights[i - 1]) {dp[i][w] = Math.max(dp[i][w], dp[i - 1][w - weights[i - 1]] + values[i - 1]);}}}return dp[n][W];}public static void main(String[] args) {Knapsack knapsack = new Knapsack();int[] weights = {2, 3, 4, 5}; // 物品的重量int[] values = {3, 4, 5, 6}; // 物品的价值int W = 5; // 背包容量int n = weights.length; // 物品数量int maxValue = knapsack.knapsack(W, weights, values, n);System.out.println("最大价值: " + maxValue); // 输出 7}
}
代码讲解:
- 二维DP数组:
dp[i][w]表示前i个物品,背包容量为w时能达到的最大价值。 - 状态转移:通过选择或不选择第
i个物品来更新dp[i][w]。 - 时间复杂度:O(n * W),其中
n是物品的数量,W是背包容量。
📖 三、最长递增子序列(LIS)
问题描述: 给定一个整数数组,求该数组的最长递增子序列(LIS)的长度。
- 数组的递增子序列是数组中的一个子序列,并且这个子序列中的元素是严格递增的。
- 我们要求的是最长递增子序列的长度。
思路与分析:
- 状态定义:
- 定义
dp[i]表示以nums[i]结尾的最长递增子序列的长度。
- 定义
- 状态转移:
- 对于每个元素
nums[i],检查它之前的所有元素nums[j],如果nums[i] > nums[j],则更新dp[i]为dp[j] + 1。
- 对于每个元素
- 最终的答案是
dp数组中的最大值。
代码实现(LIS):
public class LIS {public int lengthOfLIS(int[] nums) {if (nums == null || nums.length == 0) {return 0;}int n = nums.length;int[] dp = new int[n];// 初始化dp数组,每个位置的初始值都是1for (int i = 0; i < n; i++) {dp[i] = 1;}// 枚举每个元素,检查之前的元素for (int i = 1; i < n; i++) {for (int j = 0; j < i; j++) {if (nums[i] > nums[j]) {dp[i] = Math.max(dp[i], dp[j] + 1);}}}// 找出dp数组的最大值,即最长递增子序列的长度int maxLength = 0;for (int length : dp) {maxLength = Math.max(maxLength, length);}return maxLength;}public static void main(String[] args) {LIS lis = new LIS();int[] nums = {10, 9, 2, 5, 3, 7, 101, 18};System.out.println("最长递增子序列的长度: " + lis.lengthOfLIS(nums)); // 输出 4}
}
代码讲解:
- 动态规划数组:
dp[i]表示以nums[i]为结尾的最长递增子序列的长度。 - 双重循环:对于每个元素
nums[i],检查它之前的元素nums[j],如果满足递增条件,更新dp[i]。 - 最终结果:在
dp数组中找出最大的值即为最长递增子序列的长度。
时间复杂度:
- O(n^2),因为每个元素都需要与之前的所有元素比较。
📖 四、总结
背包问题常考点:
- 01背包问题:经典的动态规划问题,重点是理解状态转移方程,通过选择与不选择物品来更新背包容量的最大价值。
- 背包问题优化:可以使用滚动数组优化空间复杂度,将
dp数组从二维优化为一维。
最长递增子序列(LIS)常考点:
- 状态转移:LIS 是一个非常经典的动态规划问题。每个
dp[i]由之前的所有dp[j]推导出。 - 优化空间复杂度:O(n^2) 的时间复杂度较高,可以通过二分查找等优化方法将时间复杂度降到 O(n log n)。
常见易错点:
- 背包问题:忘记更新
dp[i][w],或者状态转移写反了,导致背包容量或物品数目错误。 - LIS问题:对比
nums[i] > nums[j]时,处理不当可能导致未能正确记录递增关系。
相关文章:
)
蓝桥杯 Java B 组之背包问题、最长递增子序列(LIS)
Day 4:背包问题、最长递增子序列(LIS) 📖 一、动态规划(Dynamic Programming)简介 动态规划是一种通过将复杂问题分解成更小的子问题来解决问题的算法设计思想。它主要用于解决具有最优子结构和重叠子问题…...

Git如何将一个分支的内容同步到另一个分支
在 Git 中,可以通过多种方法将一个分支的内容同步到另一个分支。以下是几种常用的方法: 1. 使用 merge 命令 这是最常见的方法,将一个分支的更改合并到另一个分支。 # 切换到目标分支 git checkout target-branch# 合并源分支的内容 git m…...

[C#]C# winform部署yolov12目标检测的onnx模型
yolov12官方框架:github.com/sunsmarterjie/yolov12 【测试环境】 vs2019 netframework4.7.2 opencvsharp4.8.0 onnxruntime1.16.3 【效果展示】 【调用代码】 using System; using System.Collections.Generic; using System.ComponentModel; using System.…...

51c大模型~合集69
我自己的原文哦~ https://blog.51cto.com/whaosoft/12221979 #7项基于SAM万物分割模型研究工作 1、CC-SAM: SAM with Cross-feature Attention and Context for Ultrasound Image Segmentation #ECCV2024 #SAM #图像分割 #医学图像 Segment Anything Model (SAM) 在自…...

2025寒假周报4
2025寒假天梯训练7-CSDN博客 眨眼间寒假训练就告一段落了,准备回校继续战斗了。这周练了3场OI赛制的篮球杯,感觉非常糟糕,不像天梯赛,天梯赛打起来非常舒适顺畅,一直都不喜欢OI赛制,打着非常不稳定..还需要…...

自学Java-AI结合GUI开发一个石头迷阵的游戏
自学Java-AI结合GUI开发一个石头迷阵的游戏 准备环节1、创建石头迷阵的界面2、打乱顺序3、控制上下左右移动4、判断是否通关5、统计移动步骤,重启游戏6、拓展问题 准备环节 技术: 1、GUI界面编程 2、二维数组 3、程序流程控制 4、面向对象编程 ∙ \bulle…...

buuctf-[极客大挑战 2019]Knife题解
一个很简单的web题,进入界面 网页名还加白给的shell,并且给的提示也很明显,给了一个一句话木马再加上菜刀,很怀疑是一个webshell题,那么直接打开蚁剑测试连接拿shell 用提示的一句话木马的密码,测试链接发现…...

Spring MVC 对象转换器:初级开发者入门指南
Spring MVC 对象转换器:初级开发者入门指南 为什么需要对象转换器? 在 Web 应用中,我们经常需要处理不同类型的对象。例如:前端数据到后端对象 :用户通过表单提交的数据通常是HttpServletRequest 对象,我们…...

语音直播交友app出海:语音直播交友系统软件源码搭建国际化发展技术层面分析
随着移动互联网的普及和全球社交需求的增长以及国内如火如荼的Ai大模型引起的全球发展热潮,语音直播软件出海成为了具有巨大发展潜力的业务领域。以下是一些关键的技术方向,将为语音直播软件在国际市场的成功推广及搭建合作奠定基础。 通信技术 实时语音…...
Web Scraper,强大的浏览器爬虫插件!
Web Scraper是一款功能丰富的浏览器扩展爬虫工具,有着直观的图形界面,无需编写代码即可自定义数据抓取规则,高效地从网页中提取结构化数据,而且它支持灵活的数据导出选项,广泛应用于电商监控、内容聚合、市场调研等多元…...

EasyRTC:基于WebRTC与P2P技术,开启智能硬件音视频交互的全新时代
在数字化浪潮的席卷下,智能硬件已成为我们日常生活的重要组成部分,从智能家居到智能穿戴,从工业物联网到远程协作,设备间的互联互通已成为不可或缺的趋势。然而,高效、低延迟且稳定的音视频交互一直是智能硬件领域亟待…...

go 定时任务 gocron timer
选型推荐(DeepSeek) 简单任务调度: 推荐使用 cron 或 gocron,它们轻量且易用。 复杂任务调度: 推荐使用 go-quartz,支持任务依赖和持久化。 分布式任务调度: 推荐使用 asynq,基于 Redis 实现,适合分布式…...

uniapp引入uview组件库(可以引用多个组件)
第一步安装 npm install uview-ui2.0.31 第二步更新uview npm update uview-ui 第三步在main.js中引入uview组件库 第四步在uni.scss中引入import "uview-ui/theme.scss"样式 第五步在文件中使用组件...

MySQL主从架构
MySQL主从架构 MySQL REPLICATION 在实际生产环境中,如果对数据库的读和写都在一个数据库服务器中操作。无论是在安全性、高可用性,还是高并发等各个方面都是完全不能满足实际需求的,因此,一般来说都是通过主从复制(…...

科普mfc100.dll丢失怎么办?有没有简单的方法修复mfc100.dll文件
当电脑频繁弹窗提示“mfc100.dll丢失”或应用程序突然闪退时,这个看似普通的系统文件已成为影响用户体验的核心痛点。作为微软基础类库(MFC)的核心组件,mfc100.dll直接关联着Visual Studio 2010开发的大量软件运行命脉。从工业设计…...
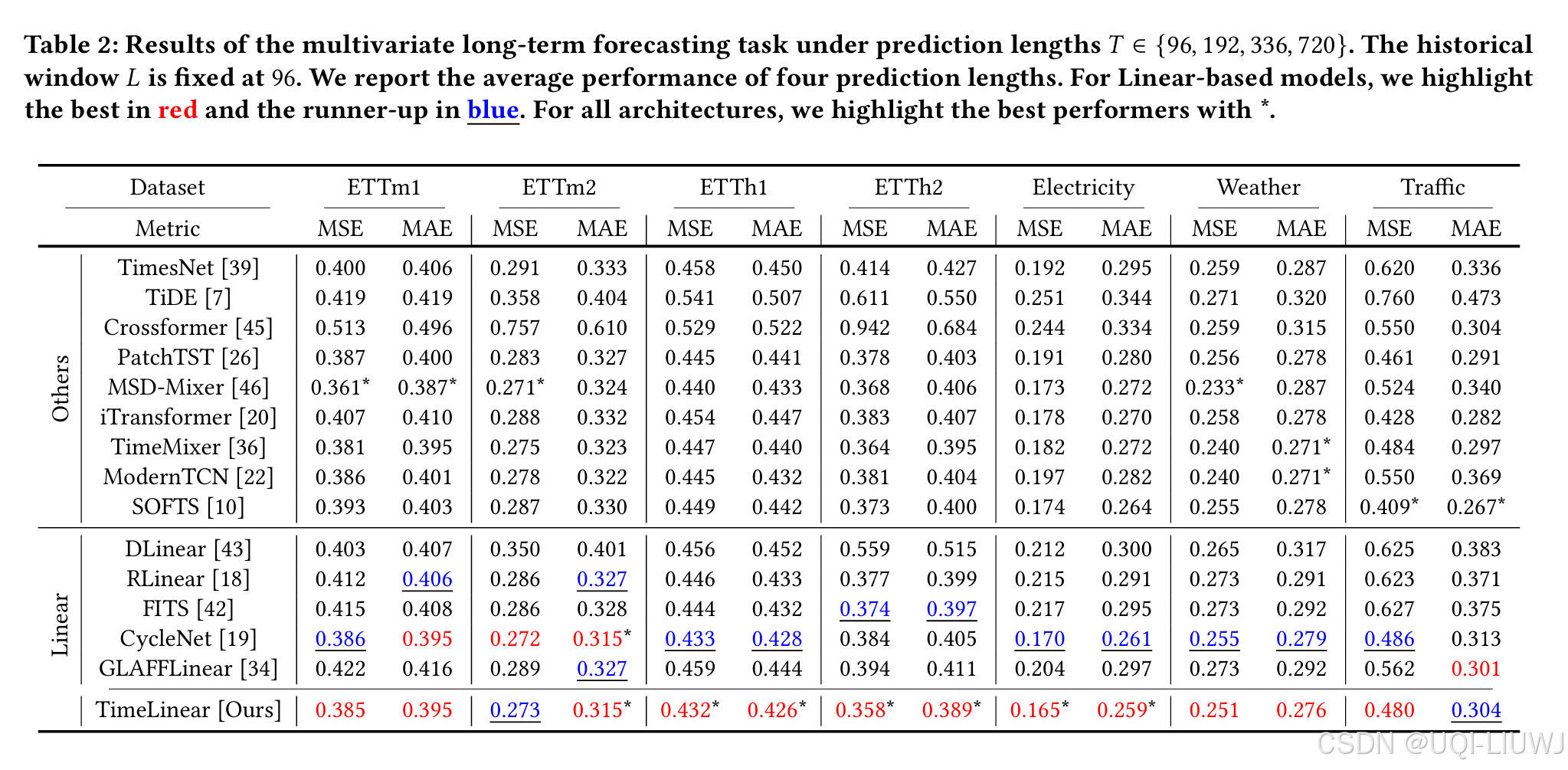
论文笔记:How Much Can Time-related Features Enhance Time Series Forecasting?
202412arxiv 许多时间序列预测方法靠变量建模,却忽略了时间戳相关特征(如季节、月份、星期几、小时、分钟等) ——>论文尝试仅基于时间戳进行预测(这个仅我觉得其实不是很严谨,还是用了时间序列变量的数据【不可能…...

Qt学习(六) 软件启动界面 ,注册表使用 ,QT绘图, 视图和窗口绘图,Graphics View绘图框架:简易CAD
一 软件启动界面 注册表使用 知识点1:这样创建的界面是不可以拖动的,需要手动创建函数来进行拖动,以下的3个函数是从父类继承过来的函数 virtual void mousePressEvent(QMouseEvent *event);virtual void mouseReleaseEvent(QMouseEvent *eve…...
--WebAssembly 基础入门)
JavaScript系列(80)--WebAssembly 基础入门
WebAssembly 基础入门 🚀 WebAssembly(简称Wasm)是一种低级的类汇编语言,它具有紧凑的二进制格式,能够以接近原生的性能在现代Web浏览器中运行。让我们深入了解这项革命性的技术。 WebAssembly 概述 🌟 &…...

蓝桥杯刷题2.21|笔记
参考的是蓝桥云课十四天的那个题单,不知道我发这个有没有问题,如果有问题找我我立马删文。(参考蓝桥云课里边的题单,跟着大佬走,应该是没错滴,加油加油) 一、握手问题 #include <iostream&g…...

053 性能压测 单机锁 setnx
文章目录 性能压测-压力测试索引thymeleafnginx减少数据库查询(代码有bug)缓存 安全单机锁(防止缓存击穿)setnx pom.xml 性能压测-压力测试 1 响应时间(Response Time: RT):响应时间指用户从客…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...

rknn toolkit2搭建和推理
安装Miniconda Miniconda - Anaconda Miniconda 选择一个 新的 版本 ,不用和RKNN的python版本保持一致 使用 ./xxx.sh进行安装 下面配置一下载源 # 清华大学源(最常用) conda config --add channels https://mirrors.tuna.tsinghua.edu.cn…...
