数据结构——二叉树经典习题讲解

 各位看官早安午安晚安呀

如果您觉得这篇文章对您有帮助的话

欢迎您一键三连，小编尽全力做到更好
欢迎您分享给更多人哦

大家好，我们今天来学习java数据结构的二叉树

递归很重要的一些注意事项：

• 1：递归你能不能掌握在于：你能不能想清楚第一层非递归 以及 递归结束的条件（也就是最后一层递归，有时候递归结束的条件可能有好几个这很常见）（结束的条件仔细想一下是否能够合并呢？return root，return null，下一层root啥也没干，root == null，是否能够合并呢？这个其实无伤大雅，但是能合并尽量还是合并一下）（这两个场景你能够想清楚，你基本思路就没什么问题）
• 2：递归有返回值的
• 2.1：如果有返回值，你大概率是要接收你下一层递归的返回值（）（然后你进行整理完之后继续向上返回）
• 2.2：递归如果返回值是要叠加的，譬如求二叉树的高度的，这个返回值一定要接收。

1.1.判断两个二叉树是否相等

链接

 public boolean isSameTree(TreeNode p, TreeNode q) {if(p == null && q != null || p != null && q == null){ //结构不一样不相等return false;}if(p == null && q == null){ // 看你俩只要同时为空就相等return true;}return p.val == q.val && isSameTree(p.left,q.left) && isSameTree(p.right,q.right);}

1.2.相同的二叉树

相同的树

public boolean isSameTree(TreeNode p, TreeNode q) {if(p == null && q != null || p != null && q == null){return false;}if(p == null && q == null){return true;}return p.val == q.val && isSameTree(p.left,q.left) && isSameTree(p.right,q.right);}public boolean isSubtree(TreeNode root, TreeNode subRoot) {if(isSameTree(root,subRoot)){ //判断一开始就是否相等return true;}if(root == null){return false;}if(isSubtree(root.left,subRoot) ||  isSubtree(root.right,subRoot)){ //左边和右边一个相等就行//其实这个就是前序遍历，利用返回值return true;}return false;}

1.3.翻转二叉树

翻转二叉树

public TreeNode invertTree(TreeNode root) {if(root == null){return null;}//交换节点TreeNode tmp = root.left;root.left = root.right;root.right = tmp;//翻转invertTree(root.left);invertTree(root.right);return root;}

1.4.平衡二叉树

平衡二叉树

补充知识点:

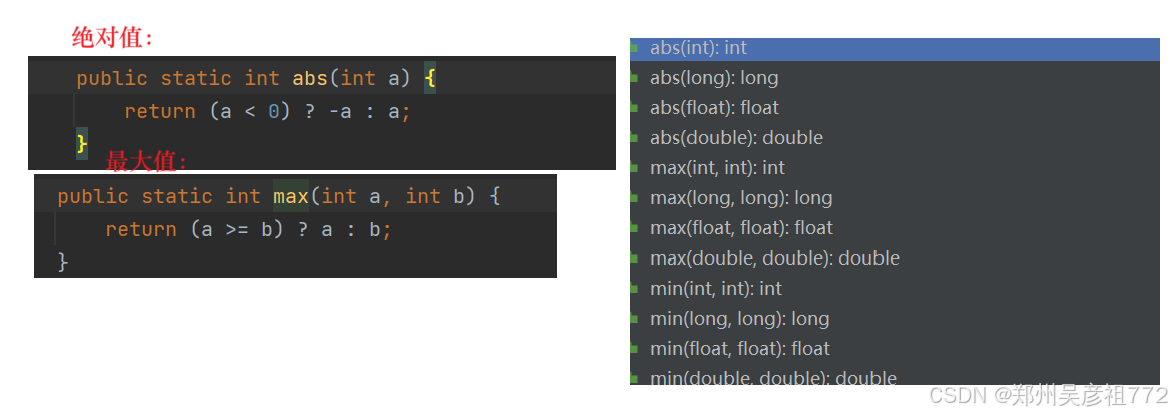
 //更改的平衡二叉树，因为我们在算高度的时候每一颗子树的高度我们都算过,我们完全可以算整个树的高度//然后进行顺带算两边的高度差是否 <= 1,一次性算完int getHeight2(TreeNode root){if(root == null){return 0;}//左树高度和右树高度int leftHeight = getHeight2(root.left);int rightHeight = getHeight2(root.right);//两边高度差<= 1并且都大于0（任何一个高度为-1的时候，整个树的返回值就为-1（-1代表不平衡））//  只要有一个-1返回，那么之后都是返回-1，不平衡if(Math.abs(leftHeight - rightHeight) <= 1 &&  leftHeight >= 0 && rightHeight >= 0){return Math.max(leftHeight,rightHeight)+1;}return -1;}public boolean isBalanced(TreeNode root) {if(root == null){return true;}     return  getHeight2(root) >= 0;}

1.5.对称二叉树

对称二叉树

public boolean isSymmetric(TreeNode root) {if(root == null){return true;}//我要看是否对称，肯定要两个节点进行比较，要两个变量return isSample(root.left,root.right);}public boolean isSample(TreeNode p , TreeNode q){//两边都是空的，就一个根，直接返回trueif( p == null && q == null){return true;}//一个为空另一个不为空，直接返回falseif( p == null || q == null){return false;}if(p.val != q.val){return false;}return isSample(p.left,q.right) && isSample(p.right,q.left);}

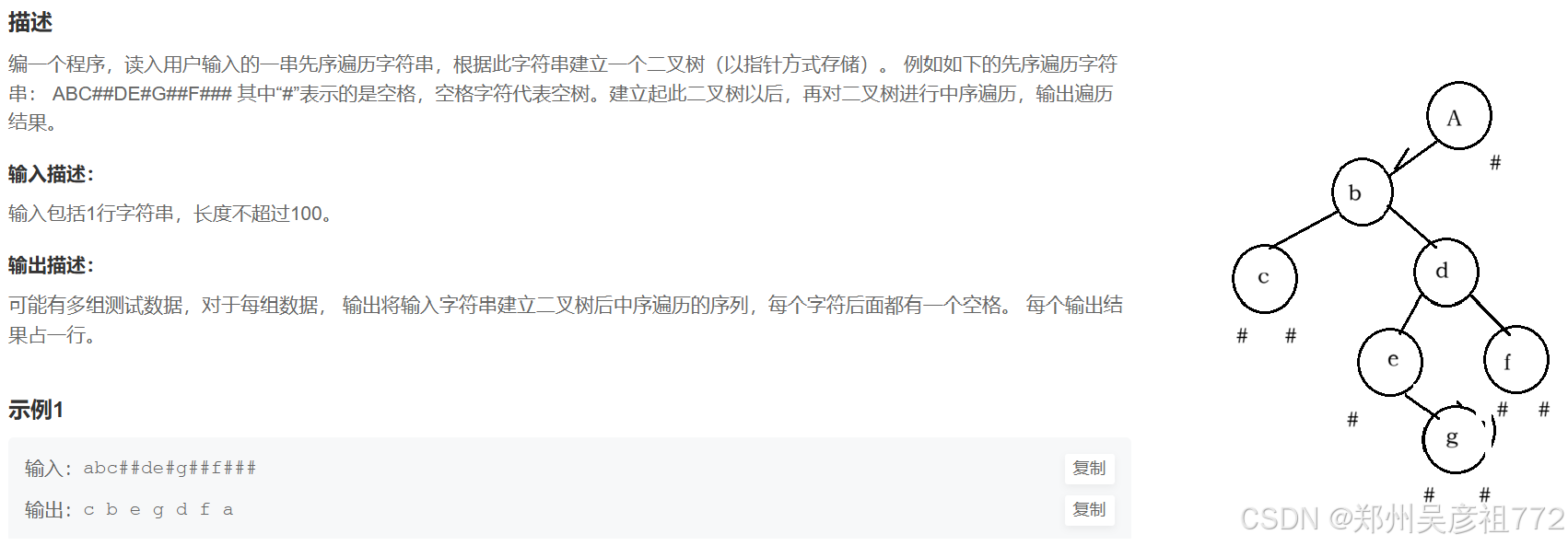
1.6.通过字符串构建二叉树

通过字符串构建二叉树

import java.util.Scanner;
class TreeNode{char val;TreeNode left;TreeNode right;public TreeNode(){}public TreeNode(char val){this.val = val;}
}// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {public static void main(String[] args) {Scanner in = new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseString str = in.nextLine();//创建二叉树TreeNode root = create(str);//中序遍历inorder(root);}}public static int i = 0;public static TreeNode create(String str){  //递归的第一层要素就是要知道什么时候结束// 首先我们遇到 “#” 就要返回 ,但是我们的i还是要先++  后返回if(str.charAt(i) == '#'){//但是我们要考虑的是，我们就算是返回了，我们的遍历str的i还是要往前走i++;return null;}else{TreeNode root = new TreeNode(str.charAt(i));i++;root.left = create(str);root.right = create(str);return root;}
//最后你会发现其实这两个返回值可以合并成一个，//其实每次递归题大家都可以看一下}//中序遍历public static void inorder(TreeNode root){if(root == null){return;}inorder(root.left);System.out.print(root.val +" ");inorder(root.right);}
}

1.7.二叉树分层遍历：

二叉树的层序遍历

public List<List<Integer>> levelOrder(TreeNode root) {List<List<Integer>> list = new ArrayList<>();//别问 问就是OJ的测试用例让我这么干的// root = []  预期结果[]，所以下面返回的也是List而不是nullif(root == null){ //如果根节点都是null，就不用遍历了return list;}// 先把 根节点add进去队列里面Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);//tmp.add(root);//这里不对呀，最后一倍一倍的增长。这个size也不对，看我下面如何修改while(!queue.isEmpty()) {//int size = tmp.size();List<Integer> tmp = new ArrayList<>();//这个可不敢放在一开始呀，不然又叠加了(ArrayList好一点)int size = queue.size();//计算上一次add进来的总和， 下面直接就是  size!=0,这完全就是要把上一次的全poll出去while (size != 0) {     //和上一个的区别就在于，上一个层序遍历是一个一个出队列的，这个是一次性把上一次add进来的全部poll出去TreeNode cur = queue.poll();tmp.add(cur.val);// System.out.println(cur.val + " ");size--;//记得--;if (cur.left != null) {queue.offer(cur.left);}if (cur.right != null) {queue.offer(cur.right);}}list.add(tmp);}return list;}

1.8.二叉树的最近公共祖先

二叉树的最近公共祖先

 public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {if(p == root || q == root){return root;}if(root == null){return null;}TreeNode leftRoot = lowestCommonAncestor(root.left,p,q);TreeNode rightRoot = lowestCommonAncestor(root.right,p,q);if(leftRoot != null && rightRoot != null){return root;} else if (leftRoot != null) {return leftRoot;}else{return rightRoot;}}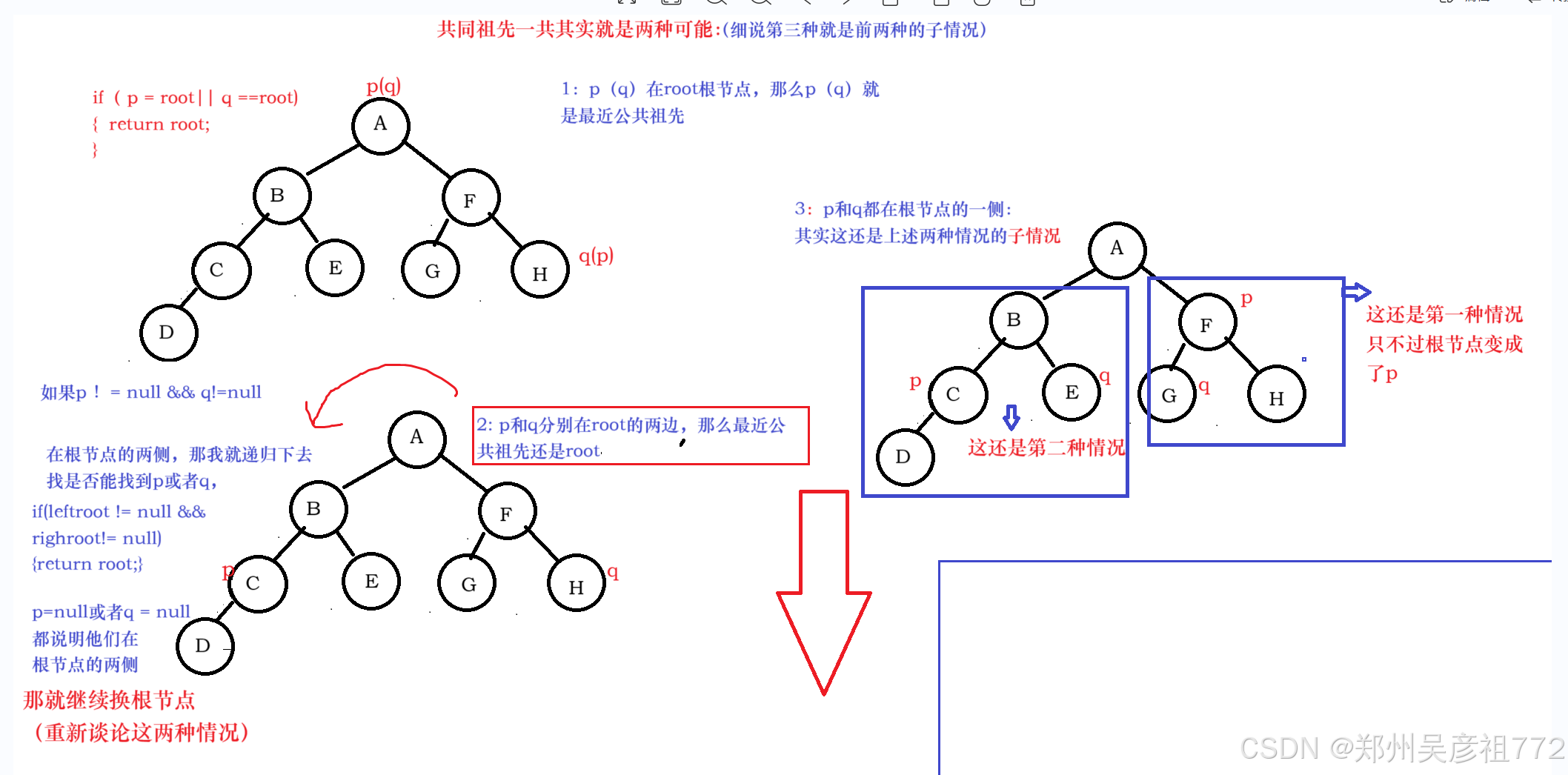

解法二：看成两个链表相交，找相交点

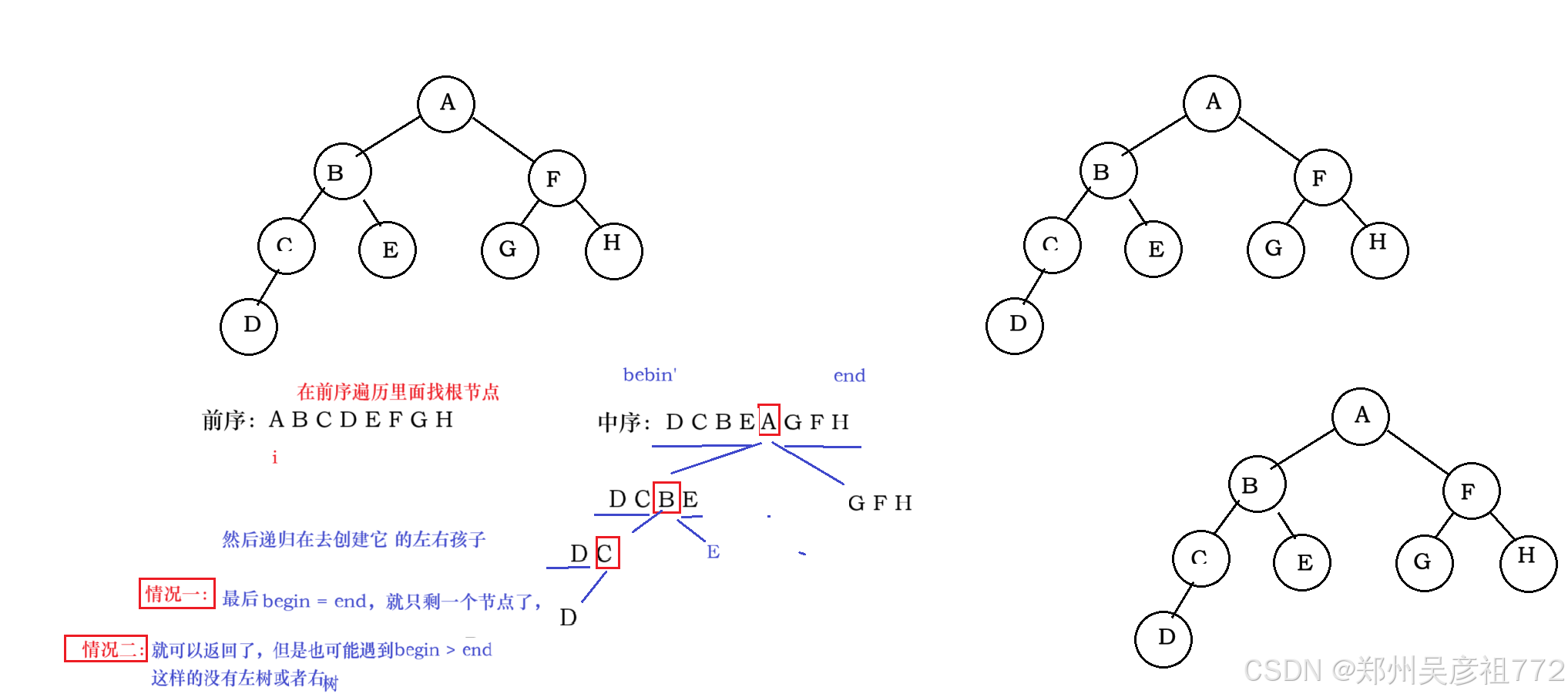
private boolean getPath(TreeNode root,TreeNode node,Stack<TreeNode>stack){// 判断这个节点是不是这个路径上的节点(如果不是，看看它的左子树和右子树是不是这个路径上的节点如果都不是)//就返回false，把这个节点pop出来if(root == null || node == null){return false;}stack.push(root);//一定要压进去，不然root == node 导致这个栈里面没有了元素if(root == node){return true;}boolean flg1 = getPath(root.left,node,stack);//看看左节点有没有if(flg1){return true;}boolean flg2 = getPath(root.right,node,stack);//看看右节点有没有if(flg2){return true;}//都没有就return falsestack.pop();return false;}public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {Stack<TreeNode>stack1 = new Stack<>();Stack<TreeNode>stack2 = new Stack<>();//利用getPath初始化这两个栈getPath(root,p,stack1);getPath(root,q,stack2);//初始化之后，进行比较，让长栈先走size步int size = stack1.size() -stack2.size();if(size > 0){while(size != 0){stack1.pop();size--;}}else{while(size != 0){stack2.pop();size++;}}while(!stack1.isEmpty() && ! stack2.isEmpty()){ //&&后面的写不写都行if(stack1.peek().equals(stack2.peek())){return stack1.peek();}stack1.pop();stack2.pop();}return null;}

1.9. 从前序与中序遍历序列构造二叉树

 从前序与中序遍历序列构造二叉树

class Solution {public int preIndex;//一定要设置成成员变量（全局效果），局部变量的话放方法参数里，每次都是传值调用//不能保证preIndex一直往前走public TreeNode buildTree(int[] preorder, int[] inorder) {return buildTreeChild(preorder,inorder,0,inorder.length -1);}private TreeNode buildTreeChild(int[] preorder,int[] inorder,int inbegin,int inend){if(inbegin > inend ){  //其实这里的结束有两次，inbegin = inend 也应该结束（但是合并成一种情况了）return null;}if(inbegin == inend){int pre = preIndex;preIndex++;return new TreeNode(preorder[pre]);}//先看这个（前序遍历的）节点是否在中序遍历的这个范围内，在的话我再把这个根节点给创建出来int rootIndex = findIndex(inorder,inbegin,inend,preorder[preIndex]);if(rootIndex == -1){return null;}TreeNode root = new TreeNode(preorder[preIndex]);preIndex++;root.left = buildTreeChild(preorder,inorder,inbegin,rootIndex-1);root.right = buildTreeChild(preorder,inorder,rootIndex + 1,inend);return root;}private int findIndex(int[] inorder,int inbegin,int inend,int key){for(int i = inbegin; i<= inend ; i++){if(inorder[i] == key){return i;}}return -1;}
}

1.10.从中序与后序遍历序列构造二叉树

如果后序：是先递归右树，再左树，再根（此刻的后序的字符串就是前序的逆转）

1从中序与后序遍历序列构造二叉树

class Solution {public int postIndex ;//一定要设置成成员变量（全局效果），局部变量的话放方法参数里，每次都是传值调用//不能保证preIndex一直往前走public TreeNode buildTree(int[] inorder, int[] postorder) {postIndex = postorder.length -1;return buildTreeChild(postorder,inorder,0,inorder.length -1);}private TreeNode buildTreeChild(int[] postorder,int[] inorder,int inbegin,int inend){if(inbegin > inend ){  //其实这里的结束有两次，inbegin = inend 也应该结束（但是合并成一种情况了）return null;}//先看这个（前序遍历的）节点是否在中序遍历的这个范围内，在的话我再把这个根节点给创建出来int rootIndex = findIndex(inorder,inbegin,inend,postorder[postIndex]);if(rootIndex == -1){return null;}TreeNode root = new TreeNode(postorder[postIndex]);postIndex--;root.right = buildTreeChild(postorder,inorder,rootIndex + 1,inend);root.left = buildTreeChild(postorder,inorder,inbegin,rootIndex-1);return root;}private int findIndex(int[] inorder,int inbegin,int inend,int key){for(int i = inbegin; i<= inend ; i++){if(inorder[i] == key){return i;}}return -1;}
}

1.11.前序遍历二叉树（迭代实现）

 public static void preOrder1(TreeNode root) {if (root == null) {return;}//本质上这还是递归的思想（stack还是往回走，不然你路上的节点，没办法遍历他的右边；Stack<TreeNode> stack = new Stack<>();TreeNode cur = root;while (cur != null || !stack.isEmpty()) {// 加个cur !=null,纯粹是因为，第一次stack是空的while (cur != null) {//一直往System.out.print(cur.val);stack.push(cur);cur = cur.left;//其实一开始我是这么想的/*if(cur == null){cur = stack.pop();cur = cur.right;//但是这样就废了呀，右边为空就完蛋了，循环结束，gameOver}*/}//左边为空，直接就拿回我上一个根，然后打印右边cur = stack.pop();cur = cur.right;}}

1.11.中序遍历二叉树（迭代实现）

public static void inOrder1(TreeNode root) {if (root == null) {return;}//本质上这还是递归的思想（stack还是往回走，不然你路上的节点，没办法遍历他的右边；Stack<TreeNode> stack = new Stack<>();TreeNode cur = root;while (cur != null || !stack.isEmpty()) {// 加个cur !=null,纯粹是因为，第一次stack是空的while (cur != null) {//一直往stack.push(cur);cur = cur.left;}//左边为空，直接就拿回我上一个根，然后打印右边cur = stack.pop();System.out.print(cur.val);cur = cur.right;}}

1.11.后序遍历二叉树（迭代实现）

  //根据字符串循环进行后序遍历public static void postOrder1(TreeNode root) {if (root == null) {return;}//本质上这还是递归的思想（stack还是往回走，不然你路上的节点，没办法遍历他的右边；Stack<TreeNode> stack = new Stack<>();TreeNode cur = root;TreeNode prev = null;TreeNode top = null;while (cur != null || !stack.isEmpty()) {// 加个cur !=null,纯粹是因为，第一次stack是空的while (cur != null) {//一直往stack.push(cur);cur = cur.left;}//左边为空，直接就拿回我上一个根，然后打印右边top = stack.peek();if(top .right == null || top.right == prev){stack.pop();System.out.print(top.val + " ");prev = top;}else {// 右边不为空不能popcur = top.right;}}}

上述就是二叉树习题讲解的全部内容了，能看到这里相信您一定对小编的文章有了一定的认可，二叉树的出现让我们对于数据的组织的利用有了更加方便的使用~~

有什么问题欢迎各位大佬指出
欢迎各位大佬评论区留言修正

您的支持就是我最大的动力​​​！！！！