三数之和:经典问题的多种优化策略
三数之和:经典问题的多种优化策略
大家好,我是Echo_Wish。今天我们来聊一个经典的算法问题——三数之和(3Sum)。它是许多面试和算法竞赛中常见的问题之一,也常常考察我们对算法优化的理解和技巧。我们不仅要解决问题,还要思考如何通过优化提高算法的效率。今天的文章将带你深入解析这个问题,并通过不同的优化策略来提高性能。
一、问题定义
三数之和的题目描述很简单:给定一个整数数组 nums,我们需要找到所有和为零的三元组,并返回这些三元组。三元组中的元素可以是重复的,但是每个三元组中的元素顺序是无关的(即 [a, b, c] 和 [c, b, a] 被认为是相同的三元组)。
比如,输入数组是 [-1, 0, 1, 2, -1, -4],我们的任务就是找到所有三元组,使得它们的和为零,答案应该是:
[[-1, -1, 2], [-1, 0, 1]]
二、暴力解法
在刚接触这个问题时,我们可能会想到暴力解法。最直观的思路是使用三重循环,枚举所有可能的三元组,判断其和是否为零。这种方法的时间复杂度是 O(n³),显然当数据量大时,效率不高。
def three_sum(nums):res = []n = len(nums)for i in range(n):for j in range(i + 1, n):for k in range(j + 1, n):if nums[i] + nums[j] + nums[k] == 0:res.append([nums[i], nums[j], nums[k]])return res
这种方法能够找到所有的解,但时间复杂度太高,尤其是在面对大规模数据时,效率非常低下。
三、双指针优化
为了优化暴力解法,我们可以考虑通过排序和双指针来提高效率。具体做法是:首先将数组进行排序,然后固定一个元素,通过双指针遍历剩下的元素,寻找两个数和为 -nums[i] 的情况。这种方法的时间复杂度降低到 O(n²)。
具体步骤如下:
- 排序:首先对数组进行排序,这样可以方便地用双指针查找和为零的三元组。
- 固定一个元素:我们通过固定第一个元素,然后在剩下的部分使用双指针查找另外两个数。
- 双指针遍历:在剩下的部分,我们使用左右两个指针分别从两端开始向中间移动。根据当前的和调整指针的位置,确保查找所有满足条件的三元组。
以下是代码实现:
def three_sum(nums):nums.sort() # 排序res = []n = len(nums)for i in range(n):if i > 0 and nums[i] == nums[i - 1]: # 跳过重复元素continueleft, right = i + 1, n - 1 # 双指针while left < right:total = nums[i] + nums[left] + nums[right]if total == 0:res.append([nums[i], nums[left], nums[right]])left += 1right -= 1# 跳过重复的元素while left < right and nums[left] == nums[left - 1]:left += 1while left < right and nums[right] == nums[right + 1]:right -= 1elif total < 0:left += 1else:right -= 1return res
在这个优化版的解法中,我们通过排序减少了重复检查的机会,并且双指针有效地缩小了搜索范围,将时间复杂度降低为 O(n²),显著提升了性能。
四、进一步优化:跳过不必要的计算
虽然双指针方法已经足够优化了,但我们依然可以进一步减少不必要的计算。特别是,在某些情况下,数组中的某些元素根本不可能构成有效的三元组,因此可以提前跳过这些元素。例如,若某个元素大于零,那么它与剩余的元素无法构成和为零的三元组,可以直接终止计算。
让我们来看看如何实现这个优化:
def three_sum(nums):nums.sort()res = []n = len(nums)for i in range(n):if nums[i] > 0: # 如果当前元素大于零,则不可能形成和为零的三元组breakif i > 0 and nums[i] == nums[i - 1]: # 跳过重复元素continueleft, right = i + 1, n - 1while left < right:total = nums[i] + nums[left] + nums[right]if total == 0:res.append([nums[i], nums[left], nums[right]])left += 1right -= 1while left < right and nums[left] == nums[left - 1]:left += 1while left < right and nums[right] == nums[right + 1]:right -= 1elif total < 0:left += 1else:right -= 1return res
在这个版本中,我们增加了一个判断条件:如果当前元素大于零,则跳出循环,因为此时已经无法组成和为零的三元组。
五、总结与展望
在解决三数之和问题时,最直接的暴力解法虽然简单易懂,但并不高效,尤其是在面对大规模数据时。通过引入排序和双指针技术,我们将时间复杂度降低到了 O(n²),这对于大多数实际应用来说已经足够高效。同时,针对不必要的计算和重复元素的跳过,也进一步优化了算法的性能。
三数之和是一个典型的面试题,掌握其基本思路和优化方法不仅有助于提高解决问题的效率,也能够帮助我们在算法设计中学会如何通过优化减少时间复杂度,提高程序的执行效率。希望通过本文的分析和优化策略,能够帮助你更好地理解并解决这个经典问题。
如果你对三数之和或其他算法问题有任何想法或疑问,欢迎在评论中与我讨论!
相关文章:

三数之和:经典问题的多种优化策略
三数之和:经典问题的多种优化策略 大家好,我是Echo_Wish。今天我们来聊一个经典的算法问题——三数之和(3Sum)。它是许多面试和算法竞赛中常见的问题之一,也常常考察我们对算法优化的理解和技巧。我们不仅要解决问题&…...

信息学奥赛一本通 1520:【 例 1】分离的路径 | 洛谷 P2860 [USACO06JAN]Redundant Paths G
【题目链接】 ybt 1520:【 例 1】分离的路径 洛谷 P2860 [USACO06JAN]Redundant Paths G 【题目考点】 1. 图论:割边(桥) 边双连通分量 【解题思路】 每个草场是一个顶点,草场之间的双向路是无向边,该…...

架构师面试(六):熔断和降级
问题 在千万日活的电商系统中,商品列表页服务通过 RPC 调用广告服务;经过统计发现,在最近10秒的时间里,商品列表页服务在对广告服务的调用中有 98% 的调用是超时的; 针对这个场景,下面哪几项的说法是正确的…...

使用 DeepSeek 生成流程图、甘特图与思维导图:结合 Typora 和 XMind 的高效工作流
在现代工作与学习中,可视化工具如流程图、甘特图和思维导图能够极大地提升信息整理与表达的效率。本文将详细介绍如何使用 DeepSeek 生成 Mermaid 文本,结合 Typora 快速生成流程图和甘特图,并通过 Markdown 格式生成思维导图,最终…...

粘贴到Word里的图片显示不全
粘贴到Word里的图片显示不全,可从Word设置、图片本身、软件与系统等方面着手解决,具体方法如下: Word软件设置 经实践发现,图片在word行距的行距出现问题,可以按照如下调整行距进行处理 修改段落行距: 选…...

【C语言】结构体内存对齐问题
1.结构体内存对齐 我们已经基本掌握了结构体的使用了。那我们现在必须得知道结构体在内存中是如何存储的?内存是如何分配的?所以我们得知道如何计算结构体的大小?这就引出了我们今天所要探讨的内容:结构体内存对齐。 1.1 对齐规…...

【蓝桥杯单片机】第十三届省赛第二场
一、真题 二、模块构建 1.编写初始化函数(init.c) void Cls_Peripheral(void); 关闭led led对应的锁存器由Y4C控制关闭蜂鸣器和继电器 2.编写LED函数(led.c) void Led_Disp(unsigned char ucLed); 将ucLed取反的值赋给P0 开启锁存器 关闭锁存…...
)
类与对象(5)
上一章是类与对象(4)-CSDN博客 深入了构造函数和静态成员,大概讲解了类型转换 最后一章最后一章 友元 在 C 中,友元提供了一种突破类的访问控制(封装)的方式。通过友元,外部的函数或类可以访…...

AI知识架构之数据采集
数据采集 数据格式: 结构化数据:以固定格式和结构存储,如数据库中的表以及 Excel 表格,易于查询和分析。半结构化数据:有一定结构但不如结构化数据严格,XML 常用于数据交换,JSON 在 Web 应用中广泛用于数据传输和存储。非结构化数据:无预定义结构,文本、图像、音频和视…...

细说STM32F407单片机2个ADC使用DMA同步采集各自的1个输入通道的方法
目录 一、示例说明 二、工程配置 1、RCC、DEBUG、CodeGenerator 2、USART6 3、TIM3 (1)Mode (2)参数设置 (3) TRGO (4)ADC1_IN0 1)ADCs_Common_Settings 2&a…...
)
C# 将非托管Dll嵌入exe中(一种实现方法)
一、环境准备 电脑系统:Windows 10 专业版 20H2 IDE:Microsoft Visual Studio Professional 2022 (64 位) - Current 版本 17.11.4 其他: 二、测试目的 将基于C++创建DLL库,封装到C#生成的exe中。 一般C++创建的库,在C#中使用,都是采用DllImport导入的,且要求库处…...

完美解决:.vmx 配置文件是由 VMware 产品创建,但该产品与此版 VMware Workstation 不兼容
参考文章:该产品与此版 VMware Workstation 不兼容,因此无法使用 问题描述 当尝试使用 VMware Workstation 打开别人的虚拟机时,可能会遇到以下报错: 此问题常见于以下场景: 从其他 VMware 版本(如 ESX…...

使用大语言模型对接OA系统,实现会议室预定功能
随着人工智能技术的不断进步,越来越多的企业开始借助 AI 助手来提高工作效率,尤其是在日常事务的自动化处理中。比如,在许多公司里,会议室的预定是一个常见且频繁的需求,通常需要员工手动检查空闲时间并做出选择。而通…...

Ryu控制器:L2交换功能实现案例
基于 Ryu控制器 在 VM1--OVS--VM2 的简单拓扑中实现流量自动下发(流表动态安装)的完整案例。通过该案例,当VM1与VM2首次通信时,Ryu控制器会动态学习路径并下发流表,后续流量将直接由交换机转发,无需控制器介…...

动手学深度学习2025.2.23-预备知识之-线性代数
3.线性代数 (1)向量维数和张量维数的区别: (2)普通矩阵乘法: 要求左矩阵的列数等于右矩阵的行数 import torch # 创建两个矩阵 A torch.tensor([[1, 2], [3, 4]], dtypetorch.float32) B torch.tensor([[5, 6], [7, 8]], d…...
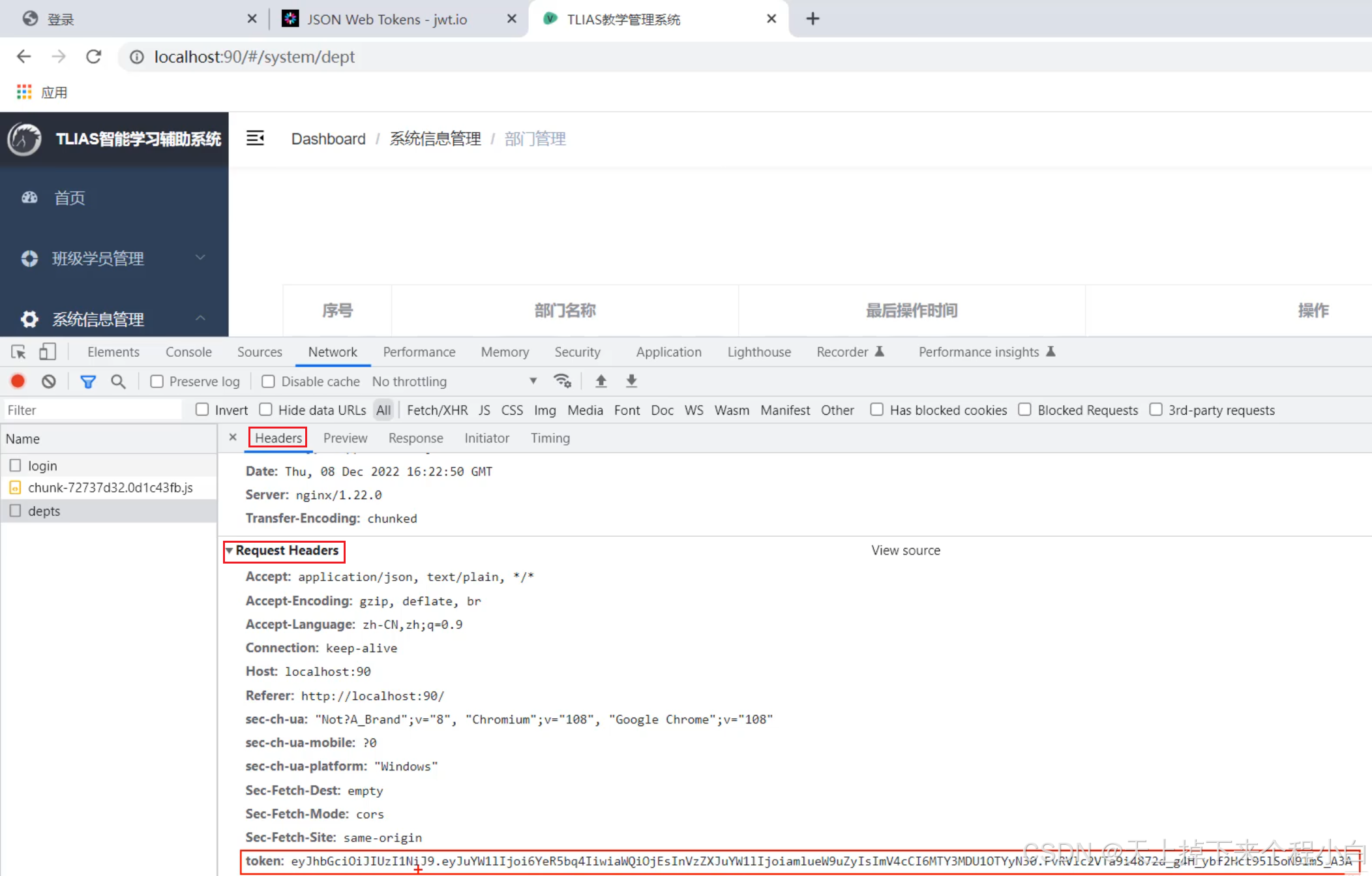
登录-07.JWT令牌-登录后下发令牌
一.思路 我们首先完成令牌生成。 在响应数据这一块 该响应数据是一个标准的Result结构,其中"data"的值就是一个JWT令牌。因此我们只需要将生成的JWT令牌封装在Result当中然后返回给前端即可。 备注是给前端看的,不用管。以后我们做校验时&…...

机器学习实战(7):聚类算法——发现数据中的隐藏模式
第7集:聚类算法——发现数据中的隐藏模式 在机器学习中,聚类(Clustering) 是一种无监督学习方法,用于发现数据中的隐藏模式或分组。与分类任务不同,聚类不需要标签,而是根据数据的相似性将其划…...

【数据序列化协议】Protocol Buffers
一、为什么需要序列化? 数据跨平台/语言交互: 不同编程语言(如 Java、Python、Go)的数据结构不兼容,序列化提供统一的数据表示。例如:Java 的 HashMap 和 Python 的 dict 需转换为通用格式(如 …...

基于 Python 的电影市场预测分析系统设计与实现(源码 + 文档)
大家好,今天要和大家聊的是一款基于 Python 的“电影市场预测分析”系统的设计与实现。项目源码以及部署相关事宜请联系我,文末附上联系方式。 项目简介 基于 Python 的“电影市场预测分析”系统主要面向以下用户角色:电影制片方、电影发行…...

计算机三级网络技术知识汇总【6】
第六章 交换机及其配置 1. 交换机基础 1.1 基本概念 局域网交换机是一种基于 MAC 地址识别,完成转发数据帧功能的一种网络连接设备。 工作在数据链路层,根据进入端口数据帧中的 MAC 地址进行数据帧的过滤、转发(也是交换机的工作原理&…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...

java高级——高阶函数、如何定义一个函数式接口类似stream流的filter
java高级——高阶函数、stream流 前情提要文章介绍一、函数伊始1.1 合格的函数1.2 有形的函数2. 函数对象2.1 函数对象——行为参数化2.2 函数对象——延迟执行 二、 函数编程语法1. 函数对象表现形式1.1 Lambda表达式1.2 方法引用(Math::max) 2 函数接口…...
