【蓝桥杯集训·每日一题2025】 AcWing 6135. 奶牛体检 python
6135. 奶牛体检
Week 1
2月21日
农夫约翰的 N N N 头奶牛站成一行,奶牛 1 1 1 在队伍的最前面,奶牛 N N N 在队伍的最后面。
农夫约翰的奶牛也有许多不同的品种。
他用从 1 1 1 到 N N N 的整数来表示每一品种。
队伍从前到后第 i i i 头奶牛的品种是 a i a_i ai。
农夫约翰正在带他的奶牛们去当地的奶牛医院进行体检。
然而,奶牛兽医非常挑剔,仅愿意当队伍中第 i i i 头奶牛为品种 b i b_i bi 时对其进行体检。
农夫约翰很懒惰,不想完全重新排列他的奶牛。
他将执行以下操作恰好一次。
- 选择两个整数 l l l 和 r r r,使得 1 ≤ l ≤ r ≤ N 1≤l≤r≤N 1≤l≤r≤N。反转队伍中第 l l l 头奶牛到第 r r r 头奶牛之间的奶牛的顺序。
农夫约翰想要衡量这种方法有多少效果。
对于每一个 c = 0 … N c=0…N c=0…N,请帮助农夫约翰求出使得恰好 c c c 头奶牛被检查的不同操作 ( l , r ) (l,r) (l,r) 的数量。
两种操作 ( l 1 , r 1 ) (l_1,r_1) (l1,r1) 和 ( l 2 , r 2 ) (l_2,r_2) (l2,r2) 不同,如果 l 1 ≠ l 2 l_1 \neq l_2 l1=l2 或者 r 1 ≠ r 2 r_1 \neq r_2 r1=r2。
输入格式
输入的第一行包含 N N N。
第二行包含 a 1 , a 2 , … , a N a_1,a_2,…,a_N a1,a2,…,aN。
第三行包含 b 1 , b 2 , … , b N b_1,b_2,…,b_N b1,b2,…,bN。
输出格式
输出 N + 1 N+1 N+1 行,第 i i i 行包含使得 i − 1 i−1 i−1 头奶牛被检查的不同操作 ( l , r ) (l,r) (l,r) 的数量。
数据范围
1 ≤ N ≤ 7500 1 \le N \le 7500 1≤N≤7500,
1 ≤ a i , b i ≤ N 1 \le a_i,b_i \le N 1≤ai,bi≤N
输入样例1:
3
1 3 2
3 2 1
输出样例1:
3
3
0
0
样例1解释
如果农夫约翰选择 ( l = 1 , r = 1 ) (l=1,r=1) (l=1,r=1), ( l = 2 , r = 2 ) (l=2,r=2) (l=2,r=2) 或 ( l = 3 , r = 3 ) (l=3,r=3) (l=3,r=3),则没有奶牛将会被检查。
注意这些操作并没有改变奶牛的位置。
以下操作会导致一头奶牛被检查。
- ( l = 1 , r = 2 ) (l=1,r=2) (l=1,r=2):农夫约翰反转第一头和第二头奶牛的顺序,因此新队伍中每头奶牛的品种将为 [ 3 , 1 , 2 ] [3,1,2] [3,1,2]。第一头奶牛将会被检查。
- ( l = 2 , r = 3 ) (l=2,r=3) (l=2,r=3):农夫约翰反转第二头和第三头奶牛的顺序,因此新队伍中每头奶牛的品种将为 [ 1 , 2 , 3 ] [1,2,3] [1,2,3]。第二头奶牛将会被检查。
- ( l = 1 , r = 3 ) (l=1,r=3) (l=1,r=3):农夫约翰反转第一头,第二头和第三头奶牛的顺序,因此新队伍中每头奶牛的品种将为 [ 2 , 3 , 1 ] [2,3,1] [2,3,1]。第三头奶牛将会被检查。
输入样例2:
3
1 2 3
1 2 3
输出样例2:
0
3
0
3
样例2解释
三种导致 3 3 3 头奶牛被检查的可能操作为 ( l = 1 , r = 1 ) (l=1,r=1) (l=1,r=1), ( l = 2 , r = 2 ) (l=2,r=2) (l=2,r=2) 和 ( l = 3 , r = 3 ) (l=3,r=3) (l=3,r=3)。
输入样例3:
7
1 3 2 2 1 3 2
3 2 2 1 2 3 1
输出样例3:
0
6
14
6
2
0
0
0
样例3解释
两种导致 4 4 4 头奶牛被检查的可能操作为 ( l = 4 , r = 5 ) (l=4,r=5) (l=4,r=5) 和 ( l = 5 , r = 7 ) (l=5,r=7) (l=5,r=7)。
方法1:
枚举区间中点,向两边扩展
实现code
n = int(input())
a = list(map(int, input().split()))
b = list(map(int, input().split()))
ans = [0] * (n + 1)cnt = 0
for i in range(n):if a[i] == b[i]:cnt += 1for i in range(n):for j in range(2):sum = cntfor l in range(i, -1, -1):r = i + j + abs(l - i)if r >= n:breakif a[l] == b[r]:sum += 1if a[r] == b[l]:sum += 1if a[l] == b[l]:sum -= 1if a[r] == b[r]:sum -= 1ans[sum] += 1
print('\n'.join(map(str, ans)))
代码解释
1. 初始匹配数计算
cnt = 0
for i in range(n):if a[i] == b[i]:cnt += 1
- 这里计算初始状态下有多少奶牛的位置和品种匹配,即
a[i] == b[i]。 cnt表示初始匹配数。
2. 枚举区间中点并向两边扩展
for i in range(n):for j in range(2): # 奇数长度区间和偶数长度区间sum = cntfor l in range(i, -1, -1):r = i + j + abs(l - i)if r >= n:break# 更新匹配数if a[l] == b[r]:sum += 1if a[r] == b[l]:sum += 1if a[l] == b[l]:sum -= 1if a[r] == b[r]:sum -= 1ans[sum] += 1
-
外层循环
for i in range(n):- 枚举区间的中点
i。 - 中点可以是某个位置(奇数长度区间)或两个位置之间(偶数长度区间)。
- 枚举区间的中点
-
内层循环
for j in range(2):j用于区分奇数长度区间和偶数长度区间。- 当
j = 0时,区间长度为奇数,中点为i。 - 当
j = 1时,区间长度为偶数,中点为i和i+1。
-
内层循环
for l in range(i, -1, -1):- 从中点
i向左扩展,枚举左端点l。 - 根据
j的值计算右端点r:r = i + j + abs(l - i)。- 如果
r >= n,说明右端点超出范围,直接跳出循环。
- 从中点
-
更新匹配数:
- 反转区间
[l, r]后,更新匹配数sum:- 如果
a[l] == b[r],反转后匹配数增加 1。 - 如果
a[r] == b[l],反转后匹配数增加 1。 - 如果
a[l] == b[l],反转前匹配,反转后不匹配,匹配数减少 1。 - 如果
a[r] == b[r],反转前匹配,反转后不匹配,匹配数减少 1。
- 如果
- 反转区间
-
更新答案:
- 根据当前的匹配数
sum,更新答案数组ans[sum] += 1。
- 根据当前的匹配数
正确性分析
-
初始匹配数计算:
- 正确计算了初始状态下匹配的奶牛数量。
-
枚举区间中点并向两边扩展:
- 通过枚举中点
i和区分奇数/偶数长度区间,确保所有可能的区间[l, r]都被覆盖。 - 反转区间
[l, r]后,匹配数的更新逻辑正确:- 反转后,
a[l]和b[r]匹配,a[r]和b[l]匹配。 - 反转前,
a[l]和b[l]匹配,a[r]和b[r]匹配,反转后这些匹配会消失。
- 反转后,
- 通过枚举中点
-
时间复杂度:
- 外层循环
for i in range(n)和for j in range(2)总共迭代2n次。 - 内层循环
for l in range(i, -1, -1)最多迭代n次。 - 因此,总时间复杂度为 O(N²)。
- 外层循环
示例分析
输入样例 1:
3
1 3 2
3 2 1
- 初始匹配数
cnt = 0。 - 枚举所有区间
[l, r]:(l=1, r=1):反转后匹配数为 0。(l=2, r=2):反转后匹配数为 0。(l=3, r=3):反转后匹配数为 0。(l=1, r=2):反转后匹配数为 1。(l=2, r=3):反转后匹配数为 1。(l=1, r=3):反转后匹配数为 1。
- 输出:
3 3 0 0
方法2:
递推:区间DP
思路
-
问题分析:
- 农夫约翰的奶牛队伍有
N头奶牛,每头奶牛有一个品种。 - 兽医只愿意检查队伍中第
i头奶牛为品种b[i]的情况。 - 农夫约翰可以选择一个区间
[l, r]反转奶牛的顺序,恰好执行一次。 - 需要计算对于每个
c = 0...N,有多少种操作(l, r)使得恰好c头奶牛被检查。
- 农夫约翰的奶牛队伍有
-
关键观察:
- 反转区间
[l, r]后,区间内的奶牛顺序会反转,而区间外的奶牛顺序不变。 - 反转后,区间内的匹配数会发生变化,而区间外的匹配数不变。
- 反转区间
-
动态规划设计:
- 定义
dp[l][r]表示反转区间[l, r]后的匹配数。 - 初始化:
- 单个区间
[i, i]的反转匹配数为cnt(初始匹配数)。 - 区间长度为 2 的情况需要单独处理。
- 单个区间
- 转移:
- 对于区间
[l, r],反转后的匹配数等于dp[l + 1][r - 1] + cost,其中cost是反转区间[l, r]带来的匹配数变化。
- 对于区间
- 定义
-
统计结果:
- 遍历所有区间
[l, r],统计每种匹配数对应的操作数量。
- 遍历所有区间
代码解释
1. 初始匹配数计算
cnt = 0
for i in range(n):if a[i] == b[i]:cnt += 1
- 计算初始状态下有多少奶牛的位置和品种匹配,即
a[i] == b[i]。 cnt表示初始匹配数。
2. DP 数组初始化
for i in range(n):dp[i][i] = cnt
- 初始化单个区间
[i, i]的反转匹配数。 - 对于单个区间,反转后匹配数不变,因此
dp[i][i] = cnt。
3. 初始化区间长度为 2
for i in range(n-1):l, r = i, i+1cost = 0if a[l] == b[r]:cost += 1if a[r] == b[l]:cost += 1if a[l] == b[l]:cost -= 1if a[r] == b[r]:cost -= 1dp[l][r] = cnt + cost
- 单独处理区间长度为 2 的情况,避免越界。
- 计算反转后的匹配数,并更新
dp[l][r]。
4. DP 转移
for len in range(3, n + 1):for l in range(n - len + 1):r = l + len - 1cost = 0if a[l] == b[r]:cost += 1if a[r] == b[l]:cost += 1if a[l] == b[l]:cost -= 1if a[r] == b[r]:cost -= 1dp[l][r] = dp[l + 1][r - 1] + cost
- 枚举区间长度
len,从 3 到n。 - 对于每个区间
[l, r],计算反转后的匹配数:- 如果
a[l] == b[r],反转后匹配数增加 1。 - 如果
a[r] == b[l],反转后匹配数增加 1。 - 如果
a[l] == b[l],反转前匹配,反转后不匹配,匹配数减少 1。 - 如果
a[r] == b[r],反转前匹配,反转后不匹配,匹配数减少 1。
- 如果
- 更新
dp[l][r]的值。
5. 统计结果
for l in range(n):for r in range(l, n):ans[dp[l][r]] += 1
- 遍历所有区间
[l, r],统计每种匹配数对应的操作数量。
6. 输出结果
print('\n'.join(map(str, ans)))
- 输出每种匹配数对应的操作数量。
END
如果有更多问题或需要进一步的帮助,可以在评论区留言讨论哦!
如果喜欢的话,请给博主点个关注 谢谢
相关文章:

【蓝桥杯集训·每日一题2025】 AcWing 6135. 奶牛体检 python
6135. 奶牛体检 Week 1 2月21日 农夫约翰的 N N N 头奶牛站成一行,奶牛 1 1 1 在队伍的最前面,奶牛 N N N 在队伍的最后面。 农夫约翰的奶牛也有许多不同的品种。 他用从 1 1 1 到 N N N 的整数来表示每一品种。 队伍从前到后第 i i i 头奶牛的…...

AI发展迅速,是否还有学习前端的必要性?
今天有个小伙伴跟我讨论:“现在 AI 发展迅速,是否还有学习 JS 或者 TS 及前端知识的必要?” 我非常肯定地说: 是的,学习 JavaScript/TypeScript 以及前端知识仍然非常必要,而且在可预见的未来,…...

【数据标准】数据标准化是数据治理的基础
导读:数据标准化是数据治理的基石,它通过统一数据格式、编码、命名与语义等,全方位提升数据质量,确保准确性、完整性与一致性,从源头上杜绝错误与冲突。这不仅打破部门及系统间的数据壁垒,极大促进数据共享…...

VS2022配置FFMPEG库基础教程
1 简介 1.1 起源与发展历程 FFmpeg诞生于2000年,由法国工程师Fabrice Bellard主导开发,其名称源自"Fast Forward MPEG",初期定位为多媒体编解码工具。2004年后由Michael Niedermayer接任维护,逐步发展成为包含音视频采…...
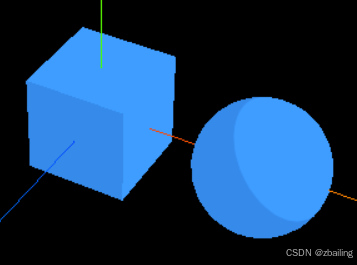
three.js之特殊材质效果
*案例42 创建一个透明的立方体 <template><div ref"container" className"container"></div> </template><script setup> import * as THREE from three; import WebGL from three/examples/jsm/capabilities/WebGL.js // 引…...

Qt常用控件之日历QCalendarWidget
日历QCalendarWidget QCalendarWidget 是一个日历控件。 QCalendarWidget属性 属性说明selectDate当前选中日期。minimumDate最小日期。maximumDate最大日期。firstDayOfWeek设置每周的第一天是周几(影响日历的第一列是周几)。gridVisible是否显示日历…...

vxe-table 如何实现跟 Excel 一样的数值或金额的负数自动显示红色字体
vxe-table 如何实现跟 Excel 一样的数值或金额的负数自动显示红色字体,当输入的值为负数时,会自动显示红色字体,对于数值或者金额输入时该功能就非常有用了。 查看官网:https://vxetable.cn gitbub:https://github.co…...

DINOv2 + yolov8 + opencv 检测卡车的可拉拽雨覆是否完全覆盖
最近是接了一个需求咨询图像处理类的,甲方要在卡车过磅的地方装一个摄像头用检测卡车的车斗雨覆是否完全, 让我大致理了下需求并对技术核心做下预研究 开发一套图像处理软件,能够实时监控经过的卡车并判断其车斗的雨覆状态。 系统需具备以下…...

算法日记27:完全背包(DFS->记忆化搜索->倒叙DP->顺序DP->空间优化)
一、暴力搜索(DFS) O ( n 2 ) O(n^2) O(n2) 1.1)思路解析 1、注意和01背包的区别在于每个物品可以无限次选择 注意在完全背包中,当一个物品被选择过一次,我们仍然需要考虑是否继续选择这个物品 01背包: …...
)
Linux 命令大全完整版(14)
5. 文件管理命令 chgrp(change group) 功能说明:变更文件或目录的所属群组。语 法:chgrp [-cfhRv][–help][–version][所属群组][文件或目录…] 或 chgrp [-cfhRv][–help][–version][–reference<参考文件或目录>][文件或目录…]补充说明&…...
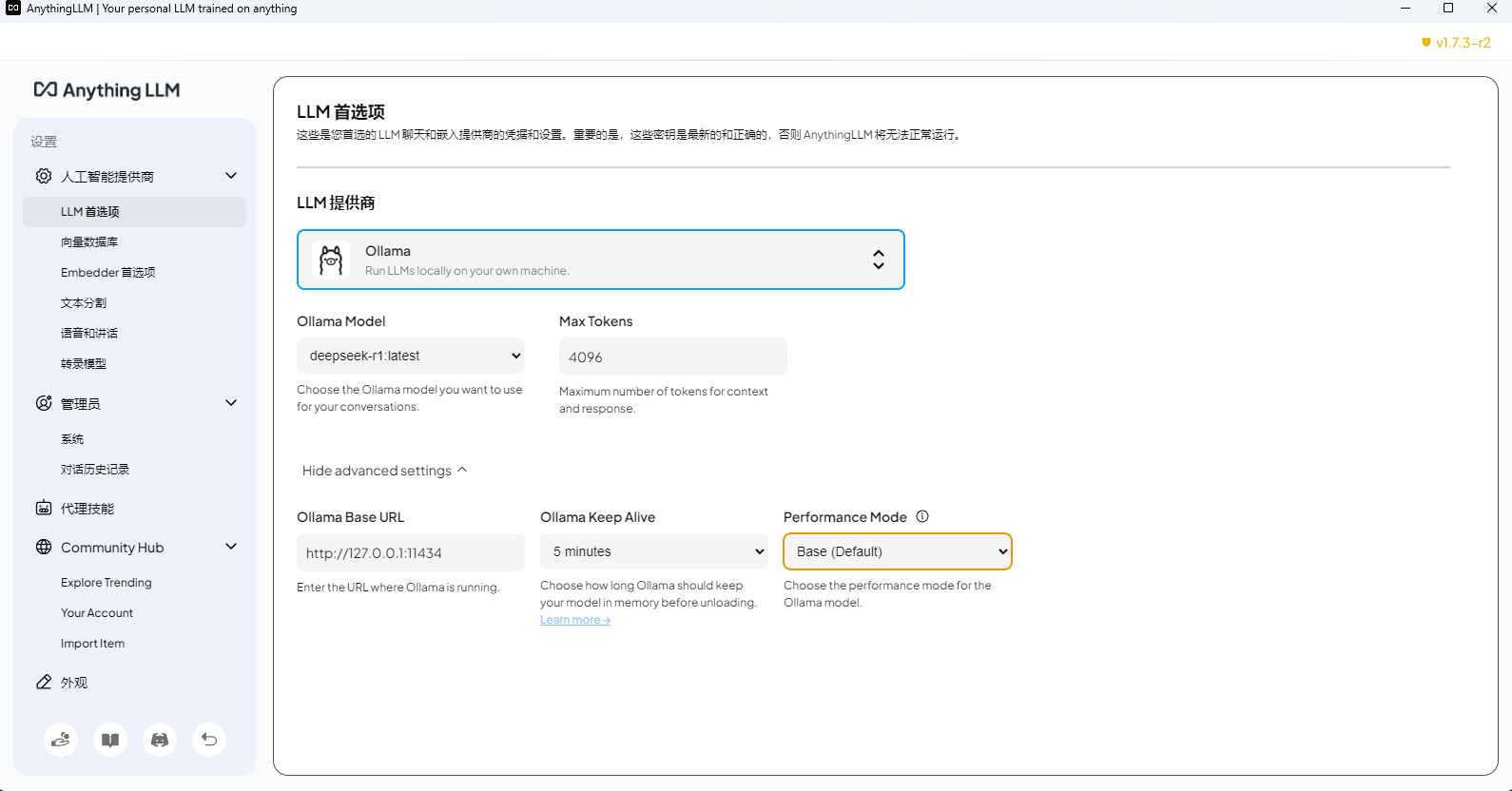
基于 DeepSeek LLM 本地知识库搭建开源方案(AnythingLLM、Cherry、Ragflow、Dify)认知
写在前面 博文内容涉及 基于 Deepseek LLM 的本地知识库搭建使用 ollama 部署 Deepseek-R1 LLM知识库能力通过 Ragflow、Dify 、AnythingLLM、Cherry 提供理解不足小伙伴帮忙指正 😃,生活加油 我站在人潮中央,思考这日日重复的生活。我突然想,…...

Could not initialize class io.netty.util.internal.Platfor...
异常信息: Exception in thread "main" java.lang.NoClassDefFoundError: Could not initialize class io.netty.util.internal.PlatformDependent0 Caused by: java.lang.ExceptionInInitializerError: Exception java.lang.reflect.InaccessibleObjec…...

【书生大模型实战营】玩转HF/魔搭/魔乐社区-L0G4000
本文是书生大模型实战营系列的第4篇,本文的主题是:玩转HF/魔搭/魔乐社区。 1.开源大模型社区总览 开源不仅仅是一种技术模式,更是一种精神的体现。它打破了知识的壁垒,让技术平权成为可能。近年来,开源大模型社区蓬勃…...

2025年华为手机解锁BL的方法
注:本文是我用老机型测试的,新机型可能不适用 背景 华为官方已经在2018年关闭了申请BL解锁码的通道,所以华为手机已经无法通过官方获取解锁码。最近翻出了一部家里的老手机华为畅玩5X,想着能不能刷个系统玩玩,但是卡…...

了解 RAG 第二部分:经典 RAG 的工作原理
在本系列的第一篇文章中,我们介绍了检索增强生成 (RAG) ,解释了扩展传统大型语言模型 (LLM)功能的必要性。我们还简要概述了 RAG 的核心思想:从外部知识库检索上下文相关的信息,以确保 LLM 生成准确且最新的信息,而不会…...

50周学习go语言:第四周 函数与错误处理深度解析
第四周 函数与错误处理深度解析 以下是第4周函数基础的深度教程,包含两个完整案例和详细实现细节: 第四周:函数与错误处理深度解析 一、函数定义与参数传递 1. 基础函数结构 // 基本语法 func 函数名(参数列表) 返回值类型 {// 函数体 }// …...

debian 12安装 postgresql 17
按照官方文档安装,即可安装成功 https://www.postgresql.org/download/linux/debian/ 添加存储库 #添加存储库 sudo apt install -y postgresql-common#执行 存储库内 命令,自动处理某些东西 sudo /usr/share/postgresql-common/pgdg/apt.postgresql.o…...

C++....................4
1. using namespace std; class mystring { private:char* p;int len;// 辅助函数:复制字符串void copy(const char* source) {len strlen(source);p new char[len 1];strcpy(p, source);}// 辅助函数:释放内存void release() {if (…...

图书馆系统源码详解
本项目是一个基于Scala语言开发的图书馆管理系统。系统主要由以下几个部分组成:数据访问层(DAO)、数据模型层(Models)、服务层(Service)以及用户界面层(UI)。以下是对项目…...

Node.js中如何修改全局变量的几种方式
Node.js中如何修改全局变量。我需要先理解他们的需求。可能他们是在开发过程中遇到了需要跨模块共享数据的情况,或者想要配置一些全局可访问的设置。不过,使用全局变量可能存在一些问题,比如命名冲突、难以维护和测试困难,所以我得…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...
