函数式编程:概念、特性与应用

1. 函数式编程简介
函数式编程,从名称上看就与函数紧密相关。它是一种我们常常使用却可能并未意识到的编程范式,关注代码的结构组织,强调一个纯粹但在实际中有些理想化的不可变世界,涉及数学、方程和副作用等概念,甚至还有有趣的“柯里化”。接下来,我们将探讨函数式编程与以往编程方式的不同之处。
代码示例
以下是一个简单的 Python 示例,展示了函数式编程中函数作为一等公民的特性:
# 定义一个简单的函数
def add(a, b):return a + b# 将函数作为参数传递给另一个函数
def apply_operation(func, x, y):return func(x, y)result = apply_operation(add, 3, 5)
print(result) # 输出: 8
2. 编程范式概述
2.1 编程范式的定义
编程范式就像一棵特殊的树,它展示了编程语言如何像口语语言一样分支成不同的家族。其中,最大的两个分支分别是命令式范式和声明式范式。
2.2 命令式与声明式范式
- 命令式范式:侧重于给出明确的指令,关注“如何做”,即详细描述程序执行的步骤。
- 声明式范式:主要描述目标,关注“做什么”,强调最终要达成的结果。
随着在这两个分支上不断深入,我们会从更通用的编程范式过渡到更具体的范式。实际上,编程范式远不止这两种。
代码示例
命令式范式(Python)
# 命令式风格:计算列表中所有偶数的和
numbers = [1, 2, 3, 4, 5, 6]
even_sum = 0
for num in numbers:if num % 2 == 0:even_sum += num
print(even_sum) # 输出: 12
声明式范式(Python)
# 声明式风格:计算列表中所有偶数的和
numbers = [1, 2, 3, 4, 5, 6]
even_sum = sum(filter(lambda x: x % 2 == 0, numbers))
print(even_sum) # 输出: 12
3. 函数式范式详解
3.1 函数式范式的位置
函数式范式位于声明式分支的大约中间位置,它概括了函数式编程与面向对象、过程式等常见范式相比所独有的概念和风格。
3.2 函数式范式的核心要素
3.2.1 一等公民函数
函数式范式的核心是函数,并且这些函数需要以较为不受限制的方式使用。这意味着我们可以将函数作为参数传递给其他函数,从其他函数中返回函数,还能保存对函数的引用以供后续使用。
代码示例(Python)
# 定义一个函数,返回另一个函数
def create_multiplier(factor):def multiplier(x):return x * factorreturn multiplier# 创建一个乘以 3 的函数
triple = create_multiplier(3)
# 使用该函数
result = triple(5)
print(result) # 输出: 15
3.2.2 闭包
- 闭包的定义:闭包是一种能够访问并记住其周围作用域的函数。在普通的函数调用栈中,函数的作用域在离开函数时会被遗忘,但闭包创建后,其作用域会一直保留在内存中,只要闭包存在。这使得我们可以从父函数返回一个闭包,并且即使在不同的作用域中调用该闭包,仍然可以访问父函数所拥有的所有参数和数据。
- 闭包示例:闭包通常是在其他函数内部定义的简单匿名函数。其特殊之处在于,即使父函数执行完毕并返回闭包后,闭包仍能访问父函数的数据。我们甚至可以在闭包中嵌套闭包,以访问最初创建第一个闭包的函数的数据。由于闭包能够以这种方式存储数据,有人用“闭包是穷人的对象,对象是穷人的闭包”来描述闭包,这有助于面向对象程序员理解闭包的概念。
代码示例(Python)
# 定义一个函数,返回一个闭包
def outer_function(x):def inner_function(y):return x + yreturn inner_function# 创建闭包
closure = outer_function(10)
# 使用闭包
result = closure(5)
print(result) # 输出: 15
3.3 函数式编程的应用方式
3.3.1 高阶函数
我们可以创建高阶函数,即与其他函数协作以执行特定操作的函数,如filter()、sort()、map()等。这些高阶函数有助于创建可复用和独立的模块,使我们能够以更声明式的方式编写代码。
代码示例(Python)
# 定义一个列表
numbers = [1, 2, 3, 4, 5]# 使用 map 函数将列表中的每个元素平方
squared_numbers = list(map(lambda x: x ** 2, numbers))
print(squared_numbers) # 输出: [1, 4, 9, 16, 25]# 使用 filter 函数过滤出列表中的偶数
even_numbers = list(filter(lambda x: x % 2 == 0, numbers))
print(even_numbers) # 输出: [2, 4]
3.3.2 不可变性与副作用
函数式编程追求不可变性,旨在避免副作用。副作用发生在函数外部的不可预测状态影响函数,或者函数对其外部作用域进行修改时。消除潜在的副作用可以使函数变得纯粹,即对于相同的输入数据,函数总是能保证产生相同的输出,且不会影响其他任何内容。这通常通过消除变量的可变性来实现。
代码示例(Python)
# 纯函数示例
def add(a, b):return a + b# 非纯函数示例(有副作用)
counter = 0
def increment():global countercounter += 1return counter# 调用纯函数
result1 = add(2, 3)
print(result1) # 输出: 5# 调用非纯函数
result2 = increment()
print(result2) # 输出: 1
3.3.3 柯里化与使用闭包模拟对象
- 柯里化:柯里化是函数式编程中的一个重要概念,它将一个函数的多个参数拆分成多个函数调用,并将这些调用链在一起。柯里化利用了闭包的作用域内存能力,每个参数会一直保留在内存中,直到调用链完成并得到最终结果。
- 模拟对象:我们可以使用闭包来创建类似对象的结构。链中的第一个函数充当对象的构造函数,在其中定义大部分内部数据。这些数据的作用域是构造函数私有的,因此被封装起来。然后,我们可以返回一个闭包,以便外部访问这些私有数据。这可用于简单的任务,如预计算和存储昂贵操作的结果(即记忆化),甚至可以返回多个命名闭包,以更复杂的方式访问和操作内部数据,进一步强化其类似对象的行为。
代码示例(Python)
柯里化
# 定义一个普通的加法函数
def add(a, b):return a + b# 实现柯里化
def curry_add(a):def inner(b):return add(a, b)return inner# 使用柯里化函数
add_five = curry_add(5)
result = add_five(3)
print(result) # 输出: 8
闭包模拟对象
def create_counter():count = 0def increment():nonlocal countcount += 1return countdef get_count():return countreturn {'increment': increment,'get_count': get_count}# 创建一个计数器对象
counter = create_counter()
# 增加计数器的值
counter['increment']()
# 获取计数器的值
print(counter['get_count']()) # 输出: 1
4. 纯函数式范式
前面介绍的只是函数式范式中常用的技术,而纯函数式范式代表着一个全新的世界,其中一切都是声明式、确定性的,并且理想情况下几乎永远不变。虽然表面上看这可能不太实用,但它源于数学领域,在数学中有很大的意义。在纯函数式范式中,主要处理类型和表达式,并遵循以下规则:
4.1 评估与执行
代码通常是被评估而不是被执行,这为我们带来了一些有趣的优化能力,如惰性评估和自动并行化。
代码示例(Python 中使用生成器实现惰性评估)
# 定义一个生成器函数
def generate_numbers():num = 0while True:yield numnum += 1# 创建生成器对象
numbers = generate_numbers()# 只获取前 5 个数字
for _ in range(5):print(next(numbers))
4.2 严格的不可变性
不可变性在所有地方都被强制执行,这意味着当我们需要对数据进行更改时,是通过基于现有常量计算出新的常量来实现的。
代码示例(Python)
# 定义一个不可变的元组
original_tuple = (1, 2, 3)
# 创建一个新的元组,基于原元组进行修改
new_tuple = original_tuple + (4,)
print(original_tuple) # 输出: (1, 2, 3)
print(new_tuple) # 输出: (1, 2, 3, 4)
4.3 单子(Monads)
为了保持函数的纯粹性,任何副作用的想法都被视为不可接受的,这就引入了单子的概念。单子是一种设计模式,用于处理函数式编程中的副作用。
代码示例(Python 中简单的 Maybe 单子示例)
class Maybe:def __init__(self, value):self.value = value@staticmethoddef unit(value):return Maybe(value)def bind(self, func):if self.value is None:return Maybe(None)return func(self.value)# 定义一个函数,可能返回 None
def divide_by_two(x):if x % 2 == 0:return Maybe(x // 2)return Maybe(None)# 使用 Maybe 单子
result = Maybe(4).bind(divide_by_two)
print(result.value) # 输出: 2
5. 函数式编程的应用与权衡
5.1 实际应用选择
纯函数式编程的世界很美好,但对于大多数程序员来说可能过于理想化。因此,我们通常会从纯函数式分支中选取一些实用的特性,并尽可能地加以利用。
5.2 函数式编程的优缺点
- 优点:函数式编程的不可变性迫使我们更严格地思考数据的传递方式,有助于确保数据不会意外更改。同时,它引导我们编写可读性高、高度模块化且易于维护的代码。
- 缺点:函数式编程可能在优化方面存在一定挑战,具体取决于在函数式分支中的使用位置。此外,对于习惯命令式编程风格的开发者来说,过渡到更声明式的编程方式可能会有一定难度。
6. 总结与鼓励
无论你是函数式程序员、面向对象程序员,还是喜欢过程式代码的简洁性,都应保持开放的心态,勇于学习新知识。即使最终不使用函数式编程,学习新事物也永远不会是浪费时间。最后,感谢视频赞助商 RunMe,它为 VS Code 提供了一个完全免费且开源的扩展,可将基本的 Markdown 文件转换为完全交互式的笔记本,方便开发者测试代码片段、记录和分享工作流程。大家可以访问 RUNME.dev 了解更多信息,并加入他们的 Discord 社区参与讨论。
相关文章:

函数式编程:概念、特性与应用
1. 函数式编程简介 函数式编程,从名称上看就与函数紧密相关。它是一种我们常常使用却可能并未意识到的编程范式,关注代码的结构组织,强调一个纯粹但在实际中有些理想化的不可变世界,涉及数学、方程和副作用等概念,甚至…...

git中的merge和rebase的区别
在 Git 中,git merge 和 git rebase 都是用于整合分支变更的核心命令,但它们的实现方式和结果有本质区别。以下是两者的详细对比: 一、核心区别 特性git mergegit rebase历史记录保留分支拓扑,生成新的合并提交线性化历史&#x…...

【目标检测】目标检测中的数据增强终极指南:从原理到实战,用Python解锁模型性能提升密码(附YOLOv5实战代码)
🧑 博主简介:曾任某智慧城市类企业算法总监,目前在美国市场的物流公司从事高级算法工程师一职,深耕人工智能领域,精通python数据挖掘、可视化、机器学习等,发表过AI相关的专利并多次在AI类比赛中获奖。CSDN…...

uniapp在app下使用mqtt协议!!!支持vue3
什么?打包空白?分享一下我的解决方法! 第一步 找大师算过了,装4.1版本运气好! 所以根目录执行命令… npm install mqtt4.1.0第二步 自己封装一个mqtt文件方便后期开坛做法! // utils/mqtt.js import mqt…...

VMware虚拟机17.5.2版本下载与安装(详细图文教程包含安装包)
文章目录 前言一、vmware虚拟机下载二、vmware虚拟机安装教程三、vmware虚拟机许可证 前言 VMware Workstation Pro 17 功能强大,广受青睐。本教程将带你一步步完成它的安装,简单易上手,助你快速搭建使用环境。 一、vmware虚拟机下载 VMwar…...

如何加固织梦CMS安全,防webshell、防篡改、防劫持,提升DedeCMS漏洞防护能力
织梦系统(DedeCMS)是一款非常知名的CMS系统,因其功能强大、结构科学合理,深受广大用户喜欢。 虽然织梦CMS(DedeCMS)非常优秀,但是为了保障网站安全,我们还是需要做一些必要的防护措…...

STM32的HAL库开发---ADC采集内部温度传感器
一、STM32内部温度传感器简介 二、温度计算方法 F1系列: 从数据手册中可以找到V25和Avg_Slope F4、F7、H7系列只是标准值不同,自行查阅手册 三、实验简要 1、功能描述 通过ADC1通道16采集芯片内部温度传感器的电压,将电压值换算成温度后&…...
)
Linux 命令大全完整版(12)
Linux 命令大全 5. 文件管理命令 ln(link) 功能说明:连接文件或目录。语 法:ln [-bdfinsv][-S <字尾备份字符串>][-V <备份方式>][--help][--version][源文件或目录][目标文件或目录] 或 ln [-bdfinsv][-S <字尾备份字符串>][-V…...

Python - 代码片段分享 - Excel 数据实时写入方法
文章目录 前言注意事项工具 pandas1. 简介2. 安装方式3. 简单介绍几个api 实战片段 - 实时写入Excel文件结束语 要么出众,要么出局 前言 我们在爬虫采集过程中,总是将数据解析抓取后统一写入Excel表格文件,如果在解析数据出现问题容易出现数据…...

(七)趣学设计模式 之 适配器模式!
目录 一、 啥是适配器模式?二、 为什么要用适配器模式?三、 适配器模式的实现方式1. 类适配器模式(继承插座 👨👩👧👦)2. 对象适配器模式(插座转换器 🔌…...

DeepSeek 细节之 MoE
DeepSeek 细节之 MoE DeepSeek 团队通过引入 MoE(Mixture of Experts,混合专家) 机制,以“分而治之”的思想,在模型容量与推理成本之间找到了精妙的平衡点,其中的技术实现和细节值得剖思 Transformer 演变…...

【Linux-网络】从逻辑寻址到物理传输:解构IP协议与ARP协议的跨层协作
🎬 个人主页:谁在夜里看海. 📖 个人专栏:《C系列》《Linux系列》《算法系列》 ⛰️ 道阻且长,行则将至 目录 📚前言 📖 IP地址的组成 🔖IPv4 🔖IPv6 📚…...

毕业离校管理系统的开发与需求分析
在当今信息化的时代背景下,高校的毕业生离校管理工作也逐渐向数字化转型。为了提高工作效率,减少人为错误,增强信息透明度,毕业离校管理系统应运而生。该系统旨在为学校提供一个高效、准确的毕业生离校管理平台,从而提…...

【NLP 24、实践 ⑤ 计算Bert模型中的参数数量】
以前不甘心,总想争个对错,现在不会了 人心各有所愿,没有道理可讲 —— 25.1.18 计算Bert模型结构中的参数数量 BertModel.from_pretrained():用于从预训练模型目录或 Hugging Face 模型库加载 BERT 模型的权重及配置。 参数名称…...

一、Spring框架系统化学习路径
系统化的Spring框架学习路径 第1阶段:基础知识准备 Java基础 核心概念:面向对象、异常处理、集合框架、多线程等。JVM基础:内存模型、垃圾回收机制。 Maven或Gradle Maven:创建项目、依赖管理、生命周期。Gradle:基本…...

Midscene.js - AI驱动,轻松实现UI自动化
UI自动化测试一直是软件测试中的一项重要任务,而随着AI技术的快速发展,自动化测试的能力也在不断提升。如何让UI自动化更智能、精准、灵活?Midscene.js作为一款AI驱动的UI自动化测试工具,正逐步改变着传统自动化测试的面貌。你是不…...

(九)Mapbox GL JS 中 Marker 图层的使用详解
什么是 Marker? 在 Mapbox GL JS 中,Marker(标记) 是一个可视化元素,用于在地图上标记特定的地理位置。它可以是一个默认的图标、自定义的图像,或者任何 HTML 元素。Marker 不仅能显示位置,还能…...
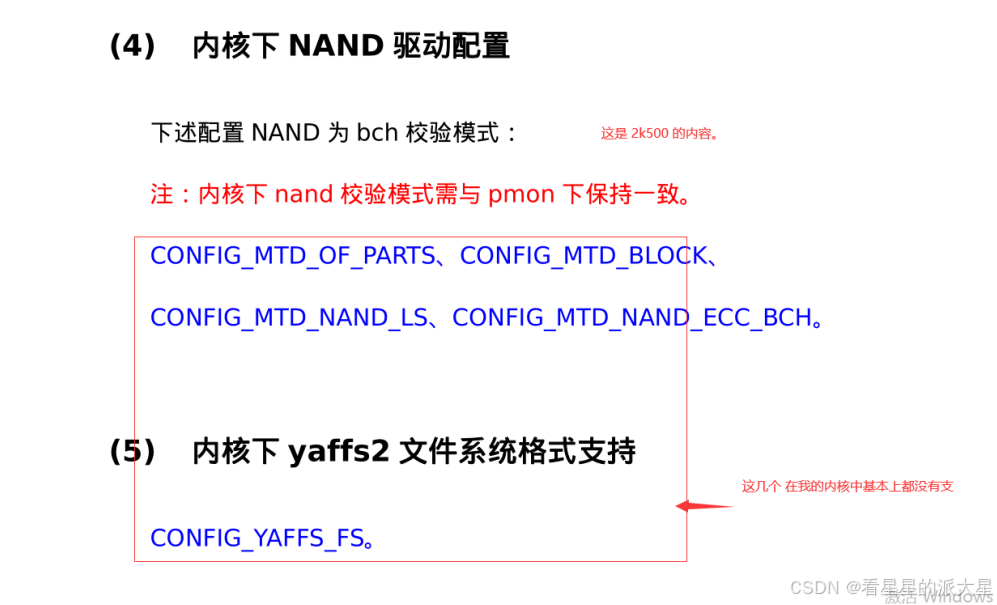
2k1000LA 使能 nand.
背景 : 默认的 发货的镜像 确实 是识别不了 nand 的。 ------------------------------------------------------------------------------------------ 但是 我之前 已经写好了文档,因此 拷贝到线上。 1 首先我要使能这几个。 在menuconfig 中使能一下。...

Junit+Mock
base project <parent><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-parent</artifactId><version>2.6.11</version><relativePath/></parent><dependencies><!--添加mysql依…...

maven编译出错,javac: ��Ч��Ŀ�귢�а�: 17
1、异常信息 javac: ��Ч��Ŀ�귢�а�: 17 ��: javac <options> <source files> -help �����г&a…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...
