补题A-E Codeforces Round 953 (Div. 2)
https://codeforces.com/contest/1979

A. Guess the Maximum
原题链接:https://codeforces.com/contest/1979/problem/A
求相邻元素的最大值的最小值。
#include <bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0), cin.tie(0), cout.tie(0)
#define ll long long
const int N = 2e5 + 5;
int n, m, k;
int a[N];
void solve() {cin >> n;for (int i = 1; i <= n; i++) {cin >> a[i];}int minmx = 1e9;for (int i = 2; i <= n; i++) {minmx = min(minmx, max(a[i - 1], a[i]));}cout << minmx - 1 << endl;
}int main() {IOS;int tt;cin >> tt;while (tt--) {solve();}return 0;
}B. XOR Sequences
原题链接:https://codeforces.com/contest/1979/problem/B
因为异或运算满足两数相同为0,不同为1。
期望是区间内的数ai = ia ^ x等于bi = ib ^ y。
满足条件的所有ia和ib一定满足:ia ^ ib等于x ^ y。
由于是求区间长度。寻找区间左端点,显然有无数对符合条件。
假如现在x ^ y等于z。
那么ia ^ ib也应该等于z,并且ia + 1 ^ ib + 1也等于z。
如果+1之后仍相等,那么低位+1时受影响的连续的1或0应该是相等的。
一直加到lowbit(z)那一位,再加会影响第lowbit(z) << 1位。
#include <bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0), cin.tie(0), cout.tie(0)
#define ll long long
const int N = 2e5 + 5;
int x, y;
int lowbit(int x) { return x & -x; }
void solve() {cin >> x >> y;cout << lowbit(x ^ y) << endl;
}int main() {IOS;int tt;cin >> tt;while (tt--) {solve();}return 0;
}C. Earning on Bets
原题链接:https://codeforces.com/contest/1979/problem/C
题目要求,期望收益大于成本。
the total amount of coins you bet on all outcomes must be strictly less than the number of coins received back for each possible winning outcome
假设每个点都投资1元,对于a[i],投资1元的期望收益是a[i]/n,总的期望收益是sum(a)/n。
需要sum(a)/n>n,假如在a[i]上再多投资1元,那么期望收益为(sum(a)+a[i])/n需大于n+1。
但如果没选到a[i]呢,损失会+1。
改动一处,会影响多处,需要尝试换个角度,减少变量数量。
如果让a[i]赢,那么投资1元的收益是a[i],失败的损失是1,这个状态转移的难点在于,难以判断a[i]上投资增加之后,与其他a[j]上收益的关系。
- 比如我在
a[i]上多投资1元,可以影响多次下注,他们必须再多投资1元,获胜收益才能大于支出。而新的投资有可能影响其他的投资。
如果让a[i]赢,那么投资1/a[i]元的收益是1元。
现在固定收益,每个点获胜都是1元,那么成本为1/a[i], i in a。
- 如果当前方案可行,那么
1大于1/a[i], i in n
假如此时不满足这个式子,那么要么提高收益,要么降低成本,显然提高收益的同时会提高成本,降低成本的同时会降低收益,假如此时成本为1.2:
- 要增加收益,那么每个点的收益都应大于
1.2,那么分母也会放缩到1.2*1.2。 - 要减去成本,那么部分点获胜的收益会减少
0.2*a[i],当该点获胜时,收益小于1,而此时总成本为1。如此递推,最终分子分母也会放缩成原来的1/1.2。
1/a[i]未必是整数。最小的整数就是lcm(a),那么每个点的投资为lcm(a)/a[i]
期望的可行方案应满足:
lcm(a)大于sum(lcm(a)/a[i]) i in n
#include <bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0), cin.tie(0), cout.tie(0)
#define ll long long
const int N = 2e5 + 5;
ll lcm(ll a, ll b) { return a / gcd(a, b) * b; }
int n;
int a[N];void solve() {cin >> n;for (int i = 1; i <= n; i++)cin >> a[i];ll L = 1;for (int i = 1; i <= n; i++)L = lcm(L, a[i]);ll S = 0;for (int i = 1; i <= n; i++)S += L / a[i];if (S >= L) {cout << "-1" << endl;return;}for (int i = 1; i <= n; i++) {cout << L / a[i] << " \n"[i == n];}
}int main() {IOS;int tt;cin >> tt;while (tt--) {solve();}return 0;
}D. Fixing a Binary String
原题链接:https://codeforces.com/problemset/problem/1979/D
题意是将一个01串分成左右两个部分,左边翻转之后追加到右边。
如果有合法的中断位置,那么,长度不等于k的连续0/1段至多两个。
翻转操作,可以拼接,断点前的最后一段和整串的最后一段,对其他段无影响。
分情况讨论即可。
#include <bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0), cin.tie(0), cout.tie(0)
#define ll long long
constexpr int N = 2e5 + 5;int n, k;
string s;
int pre[N], suf[N];
void solve() {cin >> n >> k;cin >> s;if (k == n) {int cnt = count(s.begin(), s.end(), s.front());if (cnt == n)cout << n << endl;elsecout << -1 << endl;return;}s = ' ' + s + ' ';pre[0] = suf[n + 1] = 1;for (int i = 1; i <= n; i++)pre[i] = pre[i - 1] && (i <= k || s[i] != s[i - k]);for (int i = n; i; i--)suf[i] = suf[i + 1] && (i >= n - k + 1 || s[i] != s[i + k]);int cnt = 1;for (int i = 2; i <= n; i++) {if (s[i] != s[i - 1])cnt = 1;elsecnt++;if (cnt >= k && s[i] != s[i + 1]) {int p = i - k;if (!p || !pre[p] || !suf[p + 1])continue;int flag = 1;for (int j = n - k + 1; j <= n; j++) {int x = p - (j + k - n) + 1;if (x < 1)break;if (s[x] == s[j]) {flag = 0;break;}}if (flag == 1) {cout << p << endl;return;}}}cout << -1 << endl;return;
}
int main() {IOS;int tt;cin >> tt;while (tt--) {solve();}return 0;
}E. Manhattan Triangle
原题链接:https://codeforces.com/contest/1979/problem/E
对于点i来说,曼哈顿距离为d的点,一定在一个以点i为中心,边长为$ \sqrt2d $的正方形边上。

假如正方形边框上又选定了图上这个点,那么第二点的合法点也是一个矩形,合法的交集为标注的边:

曼哈顿转切比雪夫,是将坐标系顺时针旋转45度,并放大$ \sqrt 2 $倍。
旋转前,第3点与前两点的距离都是$ \frac{d}{\sqrt2} $。
旋转后,由于放大了$ \sqrt 2 $倍,所以新的距离刚好是d。
预处理每条边,维护旋转后的横纵坐标和输入时的需要。
按新的横坐标分组并排序。
枚举每一个横坐标,他的点集应该在与x轴垂直的直线上。
- 枚举点集的每个点,找纵坐标
+d处的第2点。 - 二分搜索左右两侧的区间,有没有合法的第三点。
#include <bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0), cin.tie(0), cout.tie(0)
#define ll long long
const int N = 2e5 + 5;
using pii = pair<int, int>;
using aiii = array<int, 3>;
int n, d;
aiii p[N];
aiii ans;void fuck() {map<int, set<pii>> mp;for (int i = 1; i <= n; i++) {mp[p[i][0]].insert({p[i][1], p[i][2]});}for (auto &x : mp) {set<pii> line1 = x.second;if (mp.count(x.first + d)) {set<pii> line2 = mp[x.first + d];for (pii it0 : line1) {int y1 = it0.first;auto it1 = line1.lower_bound({y1 + d, 0});if (it1 == line1.end() || it1->first != y1 + d)continue;auto it2 = line2.lower_bound({y1, 0});if (it2 == line2.end() || it2->first > y1 + d)continue;ans = {it0.second, it1->second, it2->second};}}if (mp.count(x.first - d)) {set<pii> line2 = mp[x.first - d];for (pii it0 : line1) {int y1 = it0.first;auto it1 = line1.lower_bound({y1 + d, 0});if (it1 == line1.end() || it1->first != y1 + d)continue;auto it2 = line2.lower_bound({y1, 0});if (it2 == line2.end() || it2->first > y1 + d)continue;ans = {it0.second, it1->second, it2->second};}}}
}void solve() {cin >> n >> d;for (int i = 1; i <= n; i++) {int x, y;cin >> x >> y;p[i] = {x + y, x - y, i};}ans = {};fuck();for (int i = 1; i <= n; i++)swap(p[i][0], p[i][1]);fuck();for (int x : ans)cout << x << ' ';cout << endl;
}
signed main() {IOS;int tt = 1;cin >> tt;while (tt--) {solve();}return 0;
}相关文章:

补题A-E Codeforces Round 953 (Div. 2)
https://codeforces.com/contest/1979 A. Guess the Maximum 原题链接:https://codeforces.com/contest/1979/problem/A 求相邻元素的最大值的最小值。 #include <bits/stdc.h> using namespace std; #define IOS ios::sync_with_stdio(0), cin.tie(0), cout…...

【WordPress】发布文章时自动通过机器人推送到钉钉
在您的主题下functions.php中添加如下代码: function wpso_dingding_publish_notify($post_ID) {// 获取文章对象$post get_post($post_ID);// 检查是否是文章首次发布(即不是修订版)if (get_post_status($post_ID) publish && !g…...

鸿蒙开发深入浅出04(首页数据渲染、搜索、Stack样式堆叠、Grid布局、shadow阴影)
鸿蒙开发深入浅出04(首页数据渲染、搜索、Stack样式堆叠、Grid布局、shadow阴影) 1、效果展示2、ets/pages/Home.ets3、ets/views/Home/SearchBar.ets4、ets/views/Home/NavList.ets5、ets/views/Home/TileList.ets6、ets/views/Home/PlanList.ets7、后端…...

管道文件(1)
1.无名管道:在同一主机下,具有亲缘关系的进程间的通信,如父子进程间的通信。 2.有名管道:在同一主机下的任意进程间的通信。 (1)管道的创建 (2)管道的打开(openÿ…...

什么是AI agent技术,有哪些著名案例
AI Agent技术是一种基于人工智能的智能实体,能够感知环境、进行决策和执行动作,以实现特定目标。近年来,随着大模型(如GPT-4)和生成式AI技术的发展,AI Agent在多个领域得到了广泛应用,并取得了显…...

Cursor结合Claude 3.7零基础开发愤怒的小鸟【深夜Claude 3.7系列发布,类似DeepSeek-R1和V3的合体?】
文章目录 前言介绍“市面上唯一的混合模型”卓越的编程能力、精准控制思考时间Cursor已接入Cursor结合Claude 3.7快速编写游戏完整html代码 🍃作者介绍:双非本科大四网络工程专业在读,阿里云专家博主,前三年专注于Java领域学习&am…...
基于 Python 的天气数据分析与可视化
基于 Python 的天气数据分析与可视化 1. 项目背景 天气数据分析与可视化项目旨在通过爬取天气数据并进行分析,生成可视化图表,帮助用户了解天气变化趋势。通过该项目,学生可以掌握 Python 的数据爬取、数据分析和可视化技能。该项目适用于气…...

Bybit事件技术分析
事件概述 2025年2月21日UTC时间下午02:16:11,Bybit的以太坊冷钱包(0x1db92e2eebc8e0c075a02bea49a2935bcd2dfcf4)因恶意合约升级遭到资金盗取。根据Bybit CEO Ben Zhou的声明,攻击者通过钓鱼攻击诱骗冷钱包签名者错误签署恶意交易…...

JavaWeb-在idea中配置Servlet项目
文章目录 在idea中进行Servlet项目的配置(较新的idea版本)创建一个空的JavaSE项目(Project)创建一个普通的JavaSE板块(module)添加Web项目的配置定义一个对象模拟实现接口在web.xml中配置路径映射配置项目到Tomcat服务器启动Tomcat服务器进行测试 在idea中进行Servlet项目的配置…...

redis小记
redis小记 下载redis sudo apt-get install redis-server redis基本命令 ubuntu16下的redis没有protected-mode属性,就算sudo启动,也不能往/var/spool/cron/crontabs写计划任务,感觉很安全 #连接到redis redis-cli -h 127.0.0.1 -p 6379 …...

垂类大模型微调(一):认识LLaMA-Factory
LlamaFactory 是一个专注于 高效微调大型语言模型(LLMs) 的开源工具框架,尤其以支持 LLaMA(Meta 的大型语言模型系列)及其衍生模型(如 Chinese-LLaMA、Alpaca 等)而闻名。它的目标是简化模型微调流程,降低用户使用门槛; 官方文档 一、介绍 高效微调支持 支持多种微调…...

企业为什么要选择软件测试外包公司?湖南软件测试公司有哪些?
在当今快速发展的技术背景下,软件测试已成为软件开发生命周期的重要一环。随着企业对软件质量要求的不断提高,软件测试外包公司逐渐被越来越多的企业所青睐。 软件测试外包公司通过将软件测试从内部团队外包出去,帮助企业减少开发成本、提升…...
深度剖析与安全实践)
数据保护API(DPAPI)深度剖析与安全实践
Windows DPAPI 安全机制解析 在当今数据泄露与网络攻击日益频繁的背景下,Windows 提供的 DPAPI(Data Protection API)成为开发者保护本地敏感数据的重要工具。本文将从 双层密钥体系、加密流程、跨上下文加密、已知攻击向量与防御措施、企业…...

java23种设计模式-桥接模式
桥接模式(Bridge Pattern)学习笔记 🌟 定义 桥接模式属于结构型设计模式,将抽象部分与实现部分分离,使它们可以独立变化。通过组合代替继承的方式,解决多维度的扩展问题,防止类爆炸。 &#x…...
3D Web轻量化引擎HOOPS Communicator如何赋能航空航天制造?
在当今航空航天制造领域,精确度、效率和协作是推动行业发展的关键要素。随着数字化技术的飞速发展,3D Web可视化开发包HOOPS Communicator 为航空航天制造带来了革命性的变化。它凭借强大的功能和灵活的应用,助力企业在设计、生产、培训等各个…...
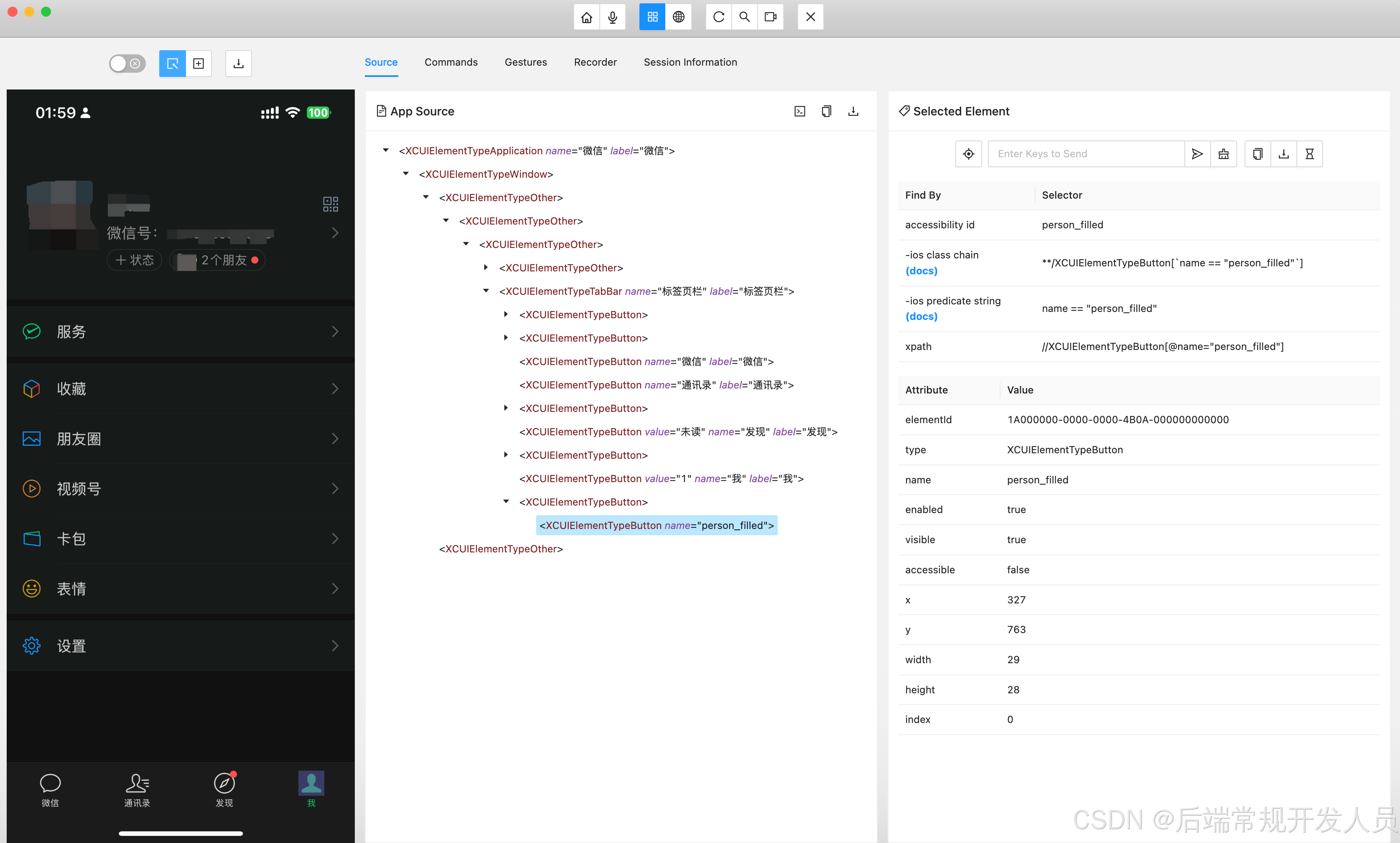
iOS手机App爬虫- (1) Mac安装Appium真机运行环境
iOS手机App爬虫 一、环境准备与工具安装1. 开发基础环境配置1.1 Node.js环境1.2 Xcode套件1.3 Java环境 2. 核心测试工具链2.1 Appium主程序2.2 辅助工具集 3. 可视化工具 二、设备与环境验证1. 设备信息获取2. 环境健康检查 三、WebDriverAgent编译部署1. 设备端准备2. 项目配…...

android s下make otapackage编译失败
[DESCRIPTION] android s上,我司推荐使用split build的方式进行编译,但是部分客户依旧会采用AOSP full build的方式进行编译。而我司在这块release的时候,并未进行验证。因此执行make otapackage的时候,会出现如下报错。 [0312/…...

《Elasticsearch实战:从零开始构建高效全文搜索引擎》
内容概览: Elasticsearch简介 Elasticsearch的定义与应用场景 Elasticsearch的核心特性 环境搭建与安装 安装Elasticsearch 启动与配置Elasticsearch 索引设计与映射 创建索引 定义映射(Mapping) 字段类型与分析器的选择 数据导入与管理…...

【Linux网络】认识协议(TCP/UDP)、Mac/IP地址和端口号、网络字节序、socket套接字
⭐️个人主页:小羊 ⭐️所属专栏:Linux 很荣幸您能阅读我的文章,诚请评论指点,欢迎欢迎 ~ 目录 1、初识协议2、UDP、TCP3、Mac、IP地址4、端口号5、网络字节序6、socket 1、初识协议 协议就是一种约定。如何让不同厂商生产的计…...

12、数据库、Sql单表多表
文章目录 一、数据库简介二、单表三、多表四、等值连接五、内联结六、inner join on、left join on、right join on区别七、模糊查找八、作业 一、数据库简介 数据在内存: 优点:读写速度快缺点:程序结束后数据丢失 保存到文件 优点&#…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...
