AWS SQS跨账户访问失败排查指南
引言
在使用AWS SQS(Simple Queue Service)时,跨账户访问是常见的业务场景。例如,账户A的应用程序向队列发送消息,账户B的消费者从队列拉取消息。尽管AWS官方文档明确支持此类配置,但在实际应用中,由于权限模型的复杂性,开发者和运维人员常会遇到“策略已配置但无法接收消息”的问题。
本文将以真实案例为基础,深入剖析跨账户SQS访问的权限模型,并逐步解决一个典型的配置问题:已正确配置SQS队列策略,但接收方仍无法查询消息。
© ivwdcwso (ID: u012172506)
一、问题背景
场景描述
- 队列所有者账户(615139160303):创建了名为
dev-sqs-track的SQS队列,并配置了队列策略(Queue Policy),允许另一个账户的特定用户和角色进行操作。 - 接收方账户(820700710557)
相关文章:

AWS SQS跨账户访问失败排查指南
引言 在使用AWS SQS(Simple Queue Service)时,跨账户访问是常见的业务场景。例如,账户A的应用程序向队列发送消息,账户B的消费者从队列拉取消息。尽管AWS官方文档明确支持此类配置,但在实际应用中,由于权限模型的复杂性,开发者和运维人员常会遇到“策略已配置但无法接…...
二刷第三十八天 | 1143. 最长公共子序列、1035. 不相交的线、53. 最大子数组和、392. 判断子序列)
算法训练(leetcode)二刷第三十八天 | 1143. 最长公共子序列、1035. 不相交的线、53. 最大子数组和、392. 判断子序列
刷题记录 1143. 最长公共子序列1035. 不相交的线53. 最大子数组和动态规划优化版 392. 判断子序列 1143. 最长公共子序列 leetcode题目地址 本题和300. 最长递增子序列相似(题解)。 使用动态规划: dp数组含义:dp[i][j]表示 以…...

【JavaWeb学习Day20】
Tlias智能学习系统 员工登录 三层架构: Controller:1.接收请求参数(用户名,密码)2.调用Service方法3.响应结果 具体实现: /*** 登录*/ PostMapping("/login") public Result login(Reque…...
等级考试试卷(二级)真题 + 答案)
2024年12月中国电子学会青少年软件编程(Python)等级考试试卷(二级)真题 + 答案
青少年软件编程(Python)等级考试试卷(二级) ↓↓↓↓↓↓ 模拟 分数:100 题数:37 一、单选题(共25题,共50分) 1. 已知字典如下 dic1 = { name: Ming, age:20, grade: A, Tel:6666666 } 以下哪个代码运行结果为20?( ) A. dic1(age) B. dic1[1] C. dic1(20) D. dic1[ag…...

一、对iic类模块分析与使用
bmp280驱动代码 说明: 1、该模块用于获取气压,温度,海拔等数据。 vcc,gnd接电源 sda ,scl 接iic通信引脚 2、该模块使用iic通信,通过iic发送请求相关类的寄存器值,芯片获取对应寄存器返回的数据…...
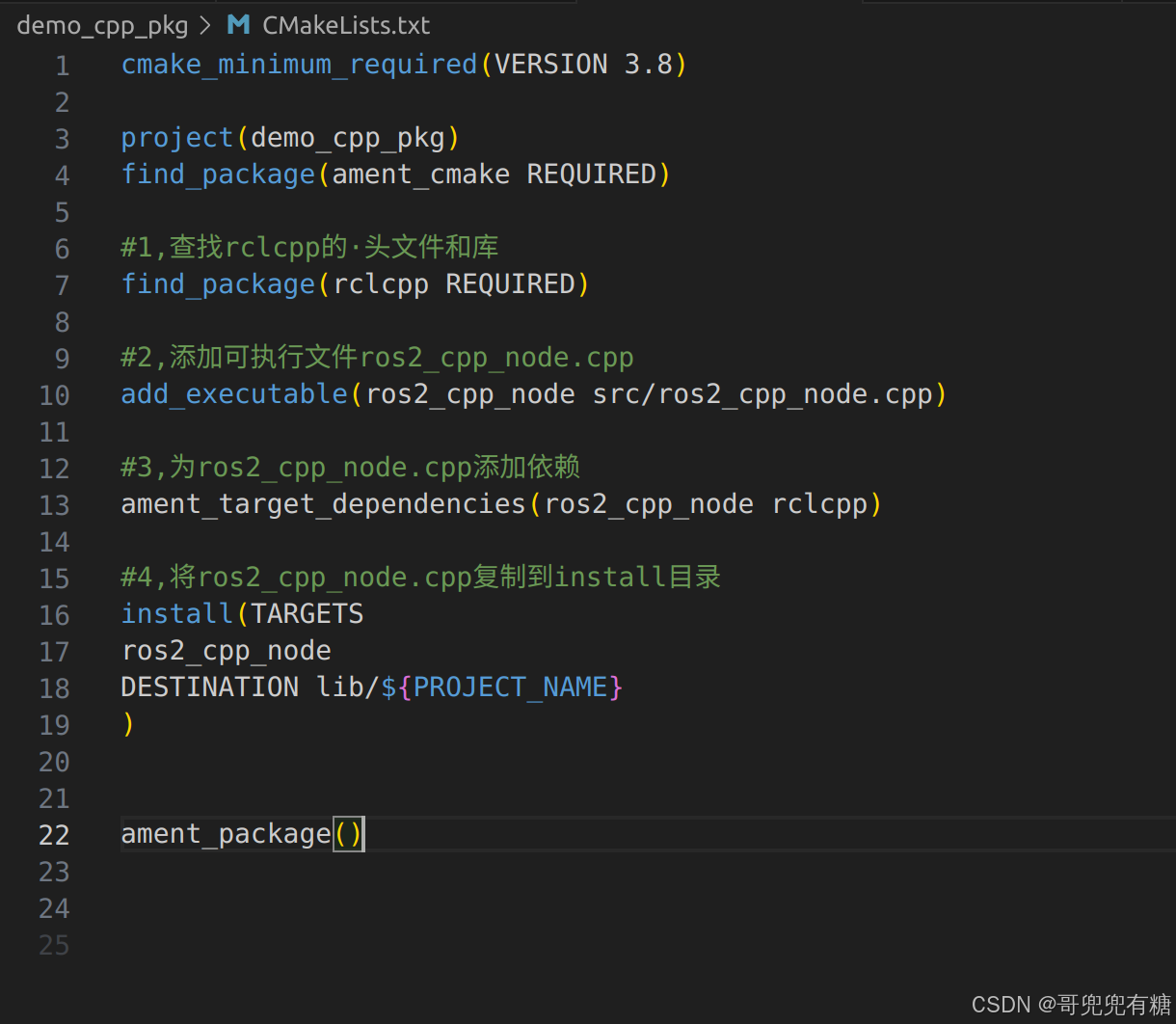
ROS 2机器人开发--CMakeLists.txt 文件详解
很多小白宝宝不懂CMakeLists.txt 究竟是干什么的,本文对CMakeLists.txt 文件进行详解 CMakeLists.txt 是 CMake 的核心文件,用户通过这个文件告诉 CMake 如何构建项目。这个文件通常包括设置项目名称、版本号、语言标准、编译器选项、查找依赖包、添加可…...

kan与小波,和不知所云的画图
文章目录 小波应用范围与pde小波的名字 画图图(a):数值解向量 \( u \)图(b):数值解向量 \( v \)结论图4 小波 在你提供的代码中,小波变换(Wavelet Transform)被用于 KANLinear 类中。具体来说,小波变换在 …...

使用DeepSeek实现自动化编程:类的自动生成
目录 简述 1. 通过注释生成C类 1.1 模糊生成 1.2 把控细节,让结果更精准 1.3 让DeepSeek自动生成代码 2. 验证DeepSeek自动生成的代码 2.1 安装SQLite命令行工具 2.2 验证DeepSeek代码 3. 测试代码下载 简述 在现代软件开发中,自动化编程工具如…...

算法题:快速排序
一、快速排序 1、快速排序总结 快速排序是一种高效的排序算法,基于分治法的思想。 分区操作是快速排序的核心,将数组分为两部分。 原地分区可以减少空间复杂度,提高效率。 快速排序的平均时间复杂度为 O(n log n),但在最坏情况…...

Python的那些事第三十六篇:基于 Vega 和 Vega-Lite 的数据可视化解决方案,Altair 声明式可视化库
Altair 声明式可视化库:基于 Vega 和 Vega-Lite 的数据可视化解决方案 摘要 在数据科学和分析领域,有效的数据可视化是理解数据、发现模式和传达见解的关键。Python 作为数据科学的主要编程语言之一,提供了多种数据可视化库。其中,Altair 是一个基于 Vega 和 Vega-Lite 的…...

aws(学习笔记第三十课) 练习使用transit gateway
aws(学习笔记第三十课) 使用transit gateway 学习内容: 什么是transit gateway构造两个vpc,并且使用session manager访问private subnet的ec2练习使用transit gateway 1. 什么是transit gateway Transit Gateway的概念 Transit Gateway就是VPC和OnPro…...

Phpstudy中的MySQL无法正常启动或启动后自动暂停,以及sqlilab环境搭建出现的问题解决方法
【解决方法】 无法启动的原因是Phpstudy中的MySQL与本地的mysql重名,导致无法正常启动;所以这时我们就需要将本地的MySQL进行修改名称; 或者修改phpstudy中数据库的端口号,但是我觉得还是不是很好解决这种问题 最后一个方法&#…...

【Android】安卓付款密码输入框、支付密码输入框
如图 代码部分: public class PayPasswordDialog extends AppCompatDialogFragment {private String mPayPass "";private String mTitle, mMoney;private final TextView[] mPayPassTextViewArray new TextView[6];private List<Integer> mPayP…...

Python异常处理:从入门到精通的实用指南
Langchain系列文章目录 01-玩转LangChain:从模型调用到Prompt模板与输出解析的完整指南 02-玩转 LangChain Memory 模块:四种记忆类型详解及应用场景全覆盖 03-全面掌握 LangChain:从核心链条构建到动态任务分配的实战指南 04-玩转 LangChai…...

【AVL树】—— 我与C++的不解之缘(二十三)
什么是AVL树? AVL树发明者是G. M. Adelson-Velsky和E. M. Landis两个前苏联科学家,他们在1962年论文《An algorithm for the organization of information》中发表了AVL树。AVL树是最先发明的自平衡二叉搜索树,说白了就是能够自己控制平衡结构…...

用大白话解释日志处理Log4j 是什么 有什么用 怎么用
Log4j是什么? Log4j就像程序的“黑匣子”,专门用来记录软件运行时的各种信息,比如哪里报错、性能如何、用户操作轨迹等。它是Java领域最常用的日志框架之一,可以灵活控制日志内容、输出位置(控制台、文件、数据库等&a…...

无人机遥控器的亮度 和 两个工作频率
工作频率 2.4000-2.4835 GHz , 5.725-5.850 GHz 1.这是一个无人机的遥控器的两个工作频率,为什么会有两个工作频率? 无人机的遥控器采用双频段设计(2.4GHz 和 5.8GHz),主要是为了解决以下问题并优化性…...

【Linux】命令行参数 | 环境变量(四)
目录 前言: 一、命令行参数: 1.main函数参数 2.为什么有它? 二、环境变量: 1.main函数第三个参数 2.查看shell本身环境变量 3.PATH环境变量 4.修改PATH环境变量配置文件 5.HOME环境变量 6.SHELL环境变量 7.PWD环境变…...

算法002——复写零
力扣——复写零点击即可跳转 这道题还是运用 双指针,我们从左往右开始,让 cur 0,dest 0,当我们循环时,会覆盖后面的值,所以从左到右无法实现,我们运用 从右到左的方式。 以示例一数组为例,从…...

例子 DQN + CartPole: 深入思考一下,强化学习确实是一场智能冒险之旅!
强化学习的概念 在技术人员眼里,深度学习、强化学习,或者是大模型,都只是一些算法。无论是简单,还是复杂,我们都是平静的看待。当商业元素日益渗透进技术领域,人人言必称大模型的时候。技术人该反思一下&a…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

从物理机到云原生:全面解析计算虚拟化技术的演进与应用
前言:我的虚拟化技术探索之旅 我最早接触"虚拟机"的概念是从Java开始的——JVM(Java Virtual Machine)让"一次编写,到处运行"成为可能。这个软件层面的虚拟化让我着迷,但直到后来接触VMware和Doc…...

STM32标准库-ADC数模转换器
文章目录 一、ADC1.1简介1. 2逐次逼近型ADC1.3ADC框图1.4ADC基本结构1.4.1 信号 “上车点”:输入模块(GPIO、温度、V_REFINT)1.4.2 信号 “调度站”:多路开关1.4.3 信号 “加工厂”:ADC 转换器(规则组 注入…...

echarts使用graphic强行给图增加一个边框(边框根据自己的图形大小设置)- 适用于无法使用dom的样式
pdf-lib https://blog.csdn.net/Shi_haoliu/article/details/148157624?spm1001.2014.3001.5501 为了完成在pdf中导出echarts图,如果边框加在dom上面,pdf-lib导出svg的时候并不会导出边框,所以只能在echarts图上面加边框 grid的边框是在图里…...

LeetCode 0386.字典序排数:细心总结条件
【LetMeFly】386.字典序排数:细心总结条件 力扣题目链接:https://leetcode.cn/problems/lexicographical-numbers/ 给你一个整数 n ,按字典序返回范围 [1, n] 内所有整数。 你必须设计一个时间复杂度为 O(n) 且使用 O(1) 额外空间的算法。…...
