华为OD-2024年E卷-分批萨[100分]
文章目录
- 题目描述
- 输入描述
- 输出描述
- 用例1
- 解题思路
- Python3源码
题目描述
吃货"和"馋嘴"两人到披萨店点了一份铁盘(圆形)披萨,并嘱咐店员将披萨按放射状切成大小相同的偶数个小块。但是粗心的服务员将披萨切成了每块大小都完全不同奇数块,且肉眼能分辨出大小。
由于两人都想吃到最多的披萨,他们商量了一个他们认为公平的分法:从"吃货"开始,轮流取披萨。除了第一块披萨可以任意选取外,其他都必须从缺口开始选。
他俩选披萨的思路不同。"馋嘴"每次都会选最大块的披萨,而且"吃货"知道"馋嘴"的想法。
已知披萨小块的数量以及每块的大小,求"吃货"能分得的最大的披萨大小的总和。
输入描述
第 1 行为一个正整数奇数 N,表示披萨小块数量。
- 3 ≤ N < 500
接下来的第 2 行到第 N + 1 行(共 N 行),每行为一个正整数,表示第 i 块披萨的大小
- 1 ≤ i ≤ N
披萨小块从某一块开始,按照一个方向次序顺序编号为 1 ~ N
- 每块披萨的大小范围为 [1, 2147483647]
输出描述
吃货"能分得到的最大的披萨大小的总和。
用例1
输入:
5
8
2
10
5
7
输出:
19
说明:
此例子中,有 5 块披萨。每块大小依次为 8、2、10、5、7。
按照如下顺序拿披萨,可以使"吃货"拿到最多披萨:
“吃货” 拿大小为 10 的披萨
“馋嘴” 拿大小为 5 的披萨
“吃货” 拿大小为 7 的披萨
“馋嘴” 拿大小为 8 的披萨
“吃货” 拿大小为 2 的披萨
至此,披萨瓜分完毕,"吃货"拿到的披萨总大小为 10 + 7 + 2 = 19
可能存在多种拿法,以上只是其中一种。
解题思路
给定一个环形排列的披萨数组,每块披萨有一个美味值,需要计算出从任意位置开始,能够获得的最大美味值总和。
-
环形处理:由于披萨是环形排列的,所以在选择披萨时需要考虑边界情况,即当选择了最左边或最右边的披萨后,如何循环到另一端。
-
动态规划:使用一个二维数组
dp作为记忆化存储,其中dp[L][R]表示从左边界L到右边界R能够获得的最大美味值。如果dp[L][R]已经被计算过,则直接返回该值。 -
递归计算:定义一个递归函数来计算
dp[L][R]。如果a[L](左边界的披萨美味值)大于a[R](右边界的披萨美味值),则选择L并将L向右移动一位;否则选择R并将R向左移动一位。这样递归地选择下一步,直到只剩下一块披萨。 -
递归基:当左右边界相遇时(即
L == R),说明只剩下一块披萨,直接返回这块披萨的美味值作为递归基。 -
状态转移:在递归过程中,
dp[L][R]的值是通过比较选择左边界披萨和右边界披萨后,剩下披萨的最大美味值之和来确定的。
Python3源码
# 读取披萨的数量
n = int(input())
# 读取每块披萨的美味值
arr = [int(input()) for _ in range(n)]# 初始化 dp 数组,dp为记忆化数组,用于存储已计算过的状态
dp = [[-1]*n for _ in range(n)]#计算最大披萨的函数
def cal_max(L,R):# 如果已计算过,直接返回结果if dp[L][R] != -1:return dp[L][R]# 根据美味值选择吃掉左边或右边的披萨if arr[L] > arr[R]:L = (L+1)%nelse:R = (R+n-1)%n# 如果只剩一块披萨,返回其美味值if L == R:dp[L][R] = arr[L]else:dp[L][R] = max(arr[L]+cal_max((L+1)%n,R),arr[R]+cal_max(L,(R+n-1)%n))return dp[L][R]# 初始化最大美味值为 0
ans = 0
# 计算并更新最大美味值
for i in range(n):ans = max(ans,cal_max((i+1)%n,(i+n-1)%n)+arr[i])# 输出最多能吃到的披萨的美味值总和
print(ans)
相关文章:

华为OD-2024年E卷-分批萨[100分]
文章目录 题目描述输入描述输出描述用例1解题思路Python3源码 题目描述 吃货"和"馋嘴"两人到披萨店点了一份铁盘(圆形)披萨,并嘱咐店员将披萨按放射状切成大小相同的偶数个小块。但是粗心的服务员将披萨切成了每块大小都完全不…...

SSH监控
创建/etc/ssh/sshrc文件 写入以命令 echo " 系统状态 " uptime free -h 每次登录会显示 如果在sshrc文件加入以下脚本每次登录就是执行这个脚本 # cat /etc/ssh/sshrc echo " 系统状态 " uptime free -h /usr/local/bin/monit.sh以…...

leetcode日记(74)扰乱字符串
很有难度的一题,一开始真的绕了很多思维上的弯路。 最开始的想法是递归,看到题目的时候想到动态规划但是完全没有思路应该怎么用,结果确实是递归动态规划。 最开始的想法是构建树,每一层包含这一步划分的方法(实际会…...

RV1126的OSD模块和SDL_TTF结合输出H264文件
目录 一.RV1126多线程处理输出OSD字符叠加图层的流程 1.1. VI模块的初始化 1.2. 初始化VENC模块: 1.3. 初始化RGN模块: 1.4. 绑定VI模块和VENC模块,伪代码如下 1.5. 创建多线程进行OSD字库的叠加: 1.6. 获取每一帧处理过后的…...

GEE:计算长时间序列NPP与NDVI之间的相关系数
GEE中内置了计算相关系数的函数,可以分析两个变量之间的相关性,比如要分析两个波段之间的相关性,主要用到ee.Reducer.pearsonsCorrelation()函数。 ee.Reducer.pearsonsCorrelation() 内容:创建一个双输入归约器,用于…...

水仙花数(华为OD)
题目描述 所谓水仙花数,是指一个n位的正整数,其各位数字的n次方和等于该数本身。 例如153是水仙花数,153是一个3位数,并且153 13 53 33。 输入描述 第一行输入一个整数n,表示一个n位的正整数。n在3到7之间&#x…...

【对话状态跟踪】关心整个对话过程用户完整意图变化
对话状态管理器 核心逻辑是解决键冲突和验证范围有效性, 但需依赖外部输入的正确性。在实际应用中, 可能需要结合用户提示或自动修正逻辑以提高鲁棒性。 NLU 槽 值 对儿 NLU的目的是把自然语言解析成结构化语义。结构化语义有多种表示方式,…...

【分享】网间数据摆渡系统,如何打破传输瓶颈,实现安全流转?
在数字化浪潮中,企业对数据安全愈发重视,网络隔离成为保护核心数据的重要手段。内外网隔离、办公网与研发网隔离等措施,虽为数据筑牢了防线,却也给数据传输带来了诸多难题。传统的数据传输方式在安全性、效率、管理等方面暴露出明…...

TikTok创作者市场关闭!全新平台TikTok One将带来哪些改变?
TikTok创作者市场关闭,全新平台TikTok One上线,创作者和品牌将迎来哪些新机遇? 近日,TikTok宣布关闭其原有的创作者市场(TikTok Creator Marketplace),并推出全新平台TikTok One。这一消息在社…...
LeetCode hot 100—矩阵置零
题目 给定一个 m x n 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。 示例 示例 1: 输入:matrix [[1,1,1],[1,0,1],[1,1,1]] 输出:[[1,0,1],[0,0,0],[1,0,1]]示例 2࿱…...
部署Windows Server自带“工作文件夹”实现企业网盘功能完整步骤
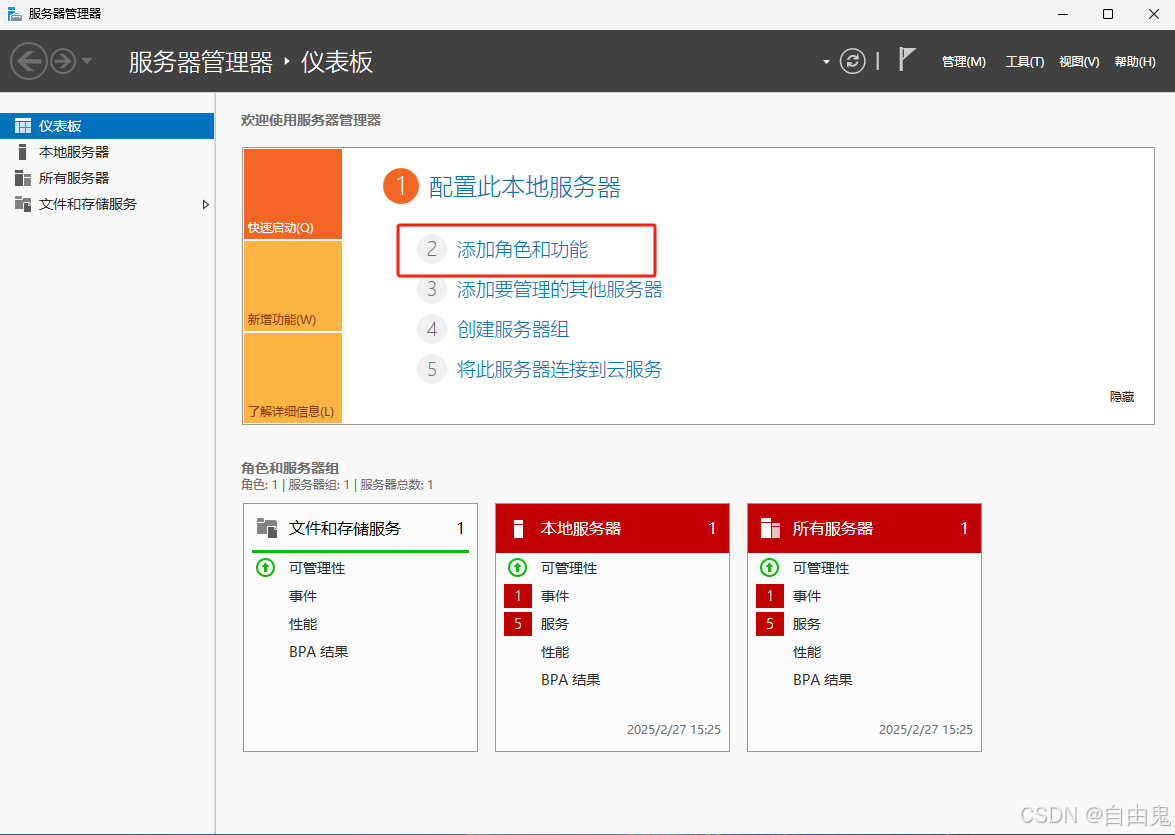
前文已经讲解过Windows Server自带的“工作文件夹”功能,现以Windows Server 2025为例介绍部署工作文件夹的完整步骤: 为了确保您能够顺利部署和充分利用工作文件夹的功能,我将按照以下步骤进行讲解。 请注意,在域环境中部署工作…...

植物大战僵尸杂交版v3.3最新版本(附下载链接)
B站游戏作者潜艇伟伟迷于12月21日更新了植物大战僵尸杂交版3.3版本!!!,有b站账户的记得要给作者三连关注一下呀! 不多废话下载链接放上: 夸克网盘链接::https://pan.quark.cn/s/6f2a…...

非关系型数据库和关系型数据库的区别
非关系型数据库(NoSQL)和关系型数据库(SQL)的主要区别体现在以下几个方面: 数据模型: 关系型数据库(SQL):数据以表格形式存储,数据行和列组成,每个…...

CPU负载高告警问题的定位与优化建议
#作者:猎人 文章目录 背景一.问题排查1.1 找到相应的容器1.2 找到对应的deployment1.3 查看pod日志1.4 查看nginx配置文件1.5 查看deployment的yaml文件 二.优化建议 背景 Docker 版本:19.03.14 Operating System: Red Hat Ent…...

2月28日,三极管测量,水利-51单片机
众所周知,三极管(BJT)有三个管脚,基极(B)、集电极(C)、发射极(E),在实际应用中,不可避免地会遇到引脚辨别的问题。接下来就讲下三极管…...

批量提取 Word 文档中的图片
在 Word 文档中,我们可以插入图片、文本、链接等各种各样的资源。在某些场景下我们需要提取这些信息,比如我们需要提取 Word 文档中的图片,将每一个 Word 文档中的图片都提取出来放到一个单独的文件夹中,那么我们应该怎么做呢&…...

C#—Settings配置详解
C#—Settings配置详解 在C#项目中,全局配置通常指的是应用程序的设置(settings),这些设置可以跨多个类或组件使用,并且通常用于存储应用程序的配置信息,如数据库连接字符串、用户偏好设置等。 Settings配置…...

UI自动化框架介绍
selenium Pytest Allure 优势 1.1 更高效的自动化测试 Selenium 提供了强大的浏览器自动化能力,可以模拟用户与网页的交互。它能够在不同浏览器上运行测试,确保 Web 应用程序在多种环境下的兼容性。Pytest 是一个非常灵活、简洁的 Python 测试框架&a…...

【工具推荐】在线提取PDF、文档、图片、论文中的公式
网址1:https://simpletex.cn/ai/latex_ocr 网址2: https://www.latexlive.com/home 推荐理由:无需下载,在线使用,直接 截图 CTRLV 效果更佳。...

帮我设计一个c语言学习阶段
以下是一个针对不同学习阶段的C语言学习计划,你可以根据自己的基础和目标进行调整: 第一阶段:基础语法与程序结构(第1-4周) 目标 熟悉C语言的基本语法和程序结构。 能够编写简单的程序。 学习内容 环境搭建 安装…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...
