贪心算法一
> 作者:დ旧言~
> 座右铭:松树千年终是朽,槿花一日自为荣。> 目标:了解什么是贪心算法,并且掌握贪心算法。
> 毒鸡汤:有些事情,总是不明白,所以我不会坚持。早安!
> 专栏选自:贪心算法_დ旧言~的博客-CSDN博客
> 望小伙伴们点赞👍收藏✨加关注哟💕💕
一、算法讲解
贪心算法的定义:
贪心算法是指在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,只做出在某种意义上的局部最优解。贪心算法不是对所有问题都能得到整体最优解,关键是贪心策略的选择,选择的贪心策略必须具备无后效性,即某个状态以前的过程不会影响以后的状态,只与当前状态有关。
解题的一般步骤是:
- 建立数学模型来描述问题;
- 把求解的问题分成若干个子问题;
- 对每一子问题求解,得到子问题的局部最优解;
- 把子问题的局部最优解合成原来问题的一个解。
如果大家比较了解动态规划,就会发现它们之间的相似之处。最优解问题大部分都可以拆分成一个个的子问题,把解空间的遍历视作对子问题树的遍历,则以某种形式对树整个的遍历一遍就可以求出最优解,大部分情况下这是不可行的。贪心算法和动态规划本质上是对子问题树的一种修剪,两种算法要求问题都具有的一个性质就是子问题最优性(组成最优解的每一个子问题的解,对于这个子问题本身肯定也是最优的)。
动态规划方法代表了这一类问题的一般解法,我们自底向上构造子问题的解,对每一个子树的根,求出下面每一个叶子的值,并且以其中的最优值作为自身的值,其它的值舍弃。而贪心算法是动态规划方法的一个特例,可以证明每一个子树的根的值不取决于下面叶子的值,而只取决于当前问题的状况。换句话说,不需要知道一个节点所有子树的情况,就可以求出这个节点的值。由于贪心算法的这个特性,它对解空间树的遍历不需要自底向上,而只需要自根开始,选择最优的路,一直走到底就可以了。
二、算法习题
2.1、第一题
题目链接:860. 柠檬水找零 - 力扣(LeetCode)
题目描述:
算法思路:
a. 遇到 5 元钱,直接收下;
b. 遇到 10 元钱,找零 5 元钱之后,收下;
c. 遇到 20 元钱:
- 先尝试凑 10 + 5 的组合;
- 如果凑不出来,拼凑 5 + 5 + 5 的组合;
代码呈现:
class Solution {
public:bool lemonadeChange(vector<int>& bills) {int five = 0, ten = 0;for (auto x : bills) {if (x == 5)five++; // 5 元:直接收下else if (x == 10) // 10 元:找零 5 元{if (five == 0)return false;five--;ten++;} else // 20 元:分情况讨论{if (ten && five) // 贪⼼{ten--;five--;} else if (five >= 3) {five -= 3;} elsereturn false;}}return true;}
};2.2、第二题
题目链接:2208. 将数组和减半的最少操作次数 - 力扣(LeetCode)
题目描述:
算法思路:
- 每次挑选出「当前」数组中「最⼤」的数,然后「减半」;
- 直到数组和减少到⾄少⼀半为⽌。
为了「快速」挑选出数组中最⼤的数,我们可以利⽤「堆」这个数据结构。
代码呈现:
class Solution {
public:int halveArray(vector<int>& nums) {priority_queue<double> heap; // 创建⼀个⼤根堆double sum = 0.0;for (int x : nums) // 把元素都丢进堆中,并求出累加和{heap.push(x);sum += x;}sum /= 2.0; // 先算出⽬标和int count = 0;while (sum > 0) // 依次取出堆顶元素减半,直到减到之前的⼀半以下{double t = heap.top() / 2.0;heap.pop();sum -= t;count++;heap.push(t);}return count;}
};2.3、第三题
题目链接:179. 最大数 - 力扣(LeetCode)
题目描述:
算法思路:
可以先优化:
将所有的数字当成字符串处理,那么两个数字之间的拼接操作以及⽐较操作就会很⽅便。
贪⼼策略:
按照题⽬的要求,重新定义⼀个新的排序规则,然后排序即可。
排序规则:
- 「A 拼接 B」 ⼤于 「B 拼接 A」,那么 A 在前,B 在后;
- 「A 拼接 B」 等于 「B 拼接 A」,那么 A B 的顺序⽆所谓;
- 「A 拼接 B」 ⼩于 「B 拼接 A」,那么 B 在前,A 在后
代码呈现:
class Solution {
public:string largestNumber(vector<int>& nums) {// 优化:把所有的数转化成字符串vector<string> strs;for (int x : nums)strs.push_back(to_string(x));// 排序sort(strs.begin(), strs.end(), [](const string& s1, const string& s2) {return s1 + s2 > s2 + s1;});// 提取结果string ret;for (auto& s : strs)ret += s;if (ret[0] == '0')return "0";return ret;}
};2.4、第四题
题目链接:376. 摆动序列 - 力扣(LeetCode)
题目描述:
算法思路:
对于某⼀个位置来说:
- 如果接下来呈现上升趋势的话,我们让其上升到波峰的位置;
- 如果接下来呈现下降趋势的话,我们让其下降到波⾕的位置。
- 因此,如果把整个数组放在「折线图」中,我们统计出所有的波峰以及波⾕的个数即可
代码呈现:
class Solution {
public:int wiggleMaxLength(vector<int>& nums) {int n = nums.size();if (n < 2)return n;int ret = 0, left = 0;for (int i = 0; i < n - 1; i++) {int right = nums[i + 1] - nums[i]; // 计算接下来的趋势if (right == 0)continue; // 如果⽔平,直接跳过if (right * left <= 0)ret++; // 累加波峰或者波⾕left = right;}return ret + 1;}
};2.5、第五题
题目链接:300. 最长递增子序列 - 力扣(LeetCode)
题目描述:
算法思路:
- 我们在考虑最⻓递增⼦序列的⻓度的时候,其实并不关⼼这个序列⻓什么样⼦,我们只是关⼼最后⼀个元素是谁。这样新来⼀个元素之后,我们就可以判断是否可以拼接到它的后⾯。
- 因此,我们可以创建⼀个数组,统计⻓度为 x 的递增⼦序列中,最后⼀个元素是谁。为了尽可能让这个序列更⻓,我们仅需统计⻓度为 x 的所有递增序列中最后⼀个元素的「最⼩值」。
- 统计的过程中发现,数组中的数呈现「递增」趋势,因此可以使⽤「⼆分」来查找插⼊位置。
代码呈现:
class Solution {
public:int lengthOfLIS(vector<int>& nums) {int n = nums.size();vector<int> ret;ret.push_back(nums[0]);for (int i = 1; i < n; i++) {if (nums[i] > ret.back()) // 如果能接在最后⼀个元素后⾯,直接放{ret.push_back(nums[i]);} else {// ⼆分插⼊位置int left = 0, right = ret.size() - 1;while (left < right) {int mid = (left + right) >> 1;if (ret[mid] < nums[i])left = mid + 1;elseright = mid;}ret[left] = nums[i]; // 放在 left 位置上}}return ret.size();}
};2.6、第六题
题目链接:334. 递增的三元子序列 - 力扣(LeetCode)
题目描述:
算法思路:
不⽤⼀个数组存数据,仅需两个变量即可。也不⽤⼆分插⼊位置,仅需两次⽐较就可以找到插⼊位
置。
代码呈现:
class Solution {
public : bool increasingTriplet(vector<int>& nums)
{int a = nums[0], b = INT_MAX;for (int i = 1; i < nums.size(); i++) {if (nums[i] > b)return true;else if (nums[i] > a)b = nums[i];elsea = nums[i];}return false;}
};三、结束语
今天内容就到这里啦,时间过得很快,大家沉下心来好好学习,会有一定的收获的,大家多多坚持,嘻嘻,成功路上注定孤独,因为坚持的人不多。那请大家举起自己的小手给博主一键三连,有你们的支持是我最大的动力💞💞💞,回见。

相关文章:

贪心算法一
> 作者:დ旧言~ > 座右铭:松树千年终是朽,槿花一日自为荣。 > 目标:了解什么是贪心算法,并且掌握贪心算法。 > 毒鸡汤:有些事情,总是不明白,所以我不会坚持。早安! >…...

什么是全栈?
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点下班 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 📃文章前言 🔷文章均为学习工…...

后端-Java虚拟机
Java虚拟机 Java虚拟机的组成 Java虚拟机的组成由类加载器ClassLoader、运行时数据区域(JVM管理的内存)和执行引擎(即时遍历器、解释器垃圾回收器) 类加载器加载class字节码文件中的内容到内存运行时数据区域负责管理jvm使用到…...

Android 低功率蓝牙之BluetoothGattCallback回调方法详解
BluetoothGattCallback 是 Android 中用于处理蓝牙低功耗(BLE)设备通信的核心回调类。它负责处理与 BLE 设备的连接、服务发现、数据读写等操作的结果。以下是对 BluetoothGattCallback 的详细解析: 1. onConnectionStateChange 触发时机&am…...

K8S学习之基础十四:k8s中Deployment控制器概述
Deployment控制器概述: Deployment控制器是k8s中最常用的资源对象,为Replicaset和Pod创建提供了一种声明式的定义方法,在Deployment对象中描述一个期望的状态,Deployment控制器就会按照一定的控制速率把实际状态改成期望状态&…...

Vue3快速入门笔记
目录 1.Vue3简介1.1.性能提升1.2.源码升级1.3.拥抱TypeScript1.4.新特性 2.创建Vue3工程2.1.基于 vue-cli 创建2.2. 基于 vite 创建(推荐)2.3.代码运行 3.Vue3核心语法3.1.OptionsAPI(选项式API) 与 CompositionAPI(组合式API)3.2.setup3.3.ref 创建&…...

【LeetCode104】二叉树的最大深度
题目 给定一个二叉树 root ,返回其最大深度。 二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。 思路与算法 树的最大深度可以通过其左子树和右子树的最大深度来定义。对于给定节点,最大深度为 1(当前节点࿰…...

SQLAlchemy系列教程:理解SQLAlchemy元数据
SQLAlchemy是Python开发人员的强大ORM工具。SQLAlchemy中的元数据是对象-关系映射配置的集合,允许开发人员无缝地定义和使用数据库模式。 使用元数据 SQLAlchemy中的元数据充当各种数据库描述符(如表、列和索引)的容器。这使开发人员能够通…...
)
Apache Shiro 反序列化漏洞全解析(Shiro-550 Shiro-721)
一、前言 Apache Shiro 是一个强大的 Java 安全框架,广泛用于用户认证、授权、加密和会话管理。然而,由于 Shiro 在某些版本中存在反序列化漏洞,攻击者可以通过特定手法实现远程代码执行(RCE),进而获取服务…...

计算机毕业设计Python+DeepSeek-R1大模型空气质量预测分析(源码+文档+PPT+讲解)
温馨提示:文末有 CSDN 平台官方提供的学长联系方式的名片! 温馨提示:文末有 CSDN 平台官方提供的学长联系方式的名片! 温馨提示:文末有 CSDN 平台官方提供的学长联系方式的名片! 作者简介:Java领…...
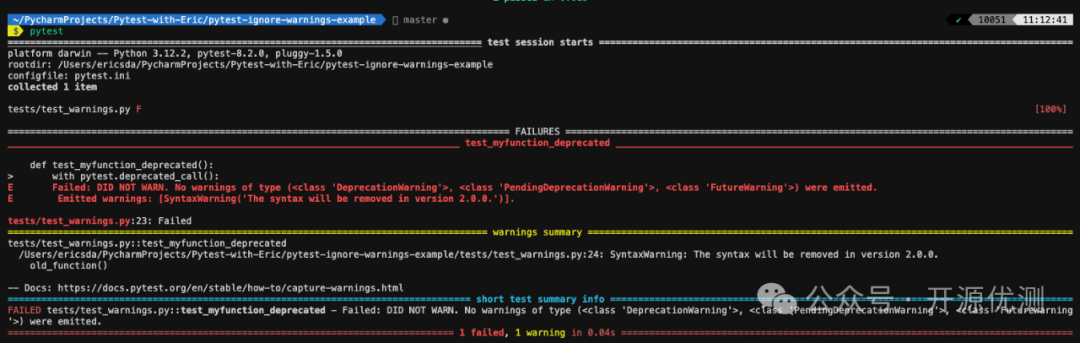
实例详细演示在Pytest中如何忽略警告
关注开源优测不迷路 大数据测试过程、策略及挑战 测试框架原理,构建成功的基石 在自动化测试工作之前,你应该知道的10条建议 在自动化测试中,重要的不是工具 当你尝试运行Pytest代码时,那些不相关的警告突然弹出,是不是…...
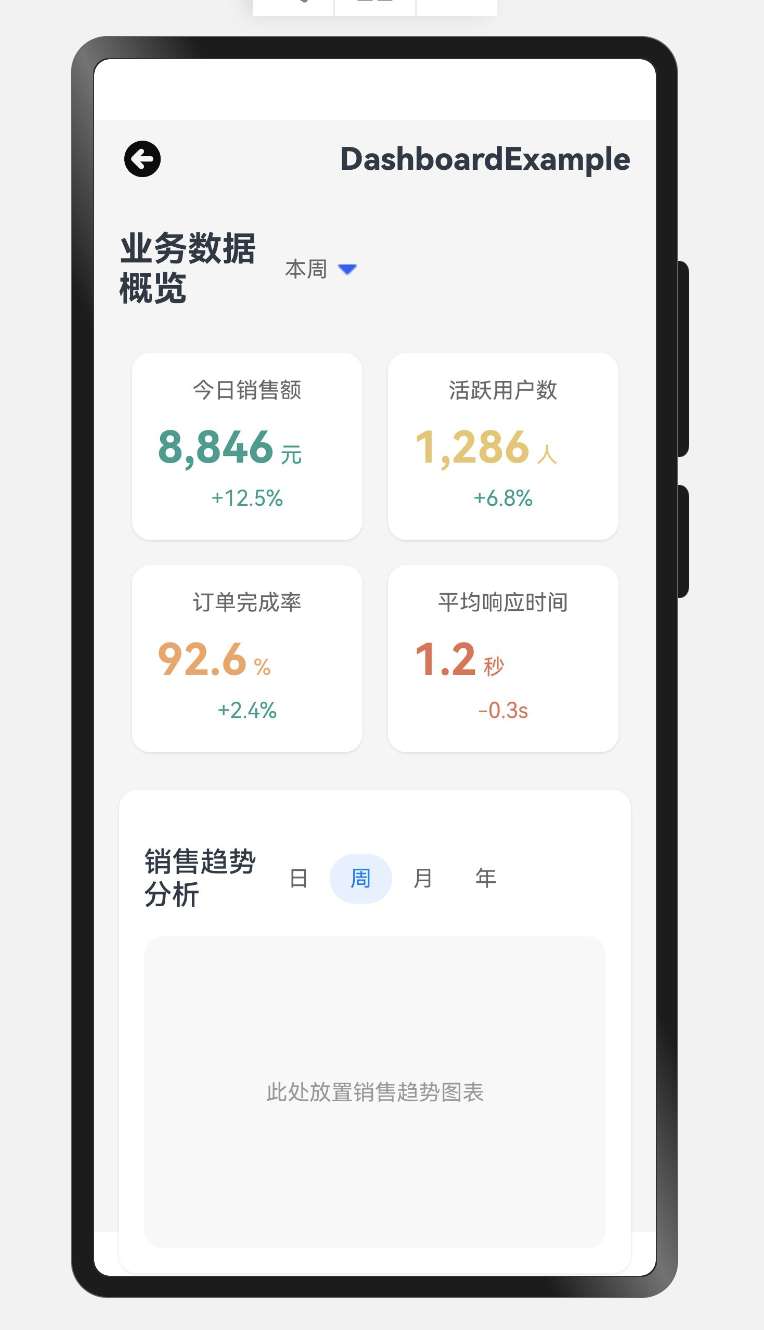
03 HarmonyOS Next仪表盘案例详解(二):进阶篇
温馨提示:本篇博客的详细代码已发布到 git : https://gitcode.com/nutpi/HarmonyosNext 可以下载运行哦! 文章目录 前言1. 响应式设计1.1 屏幕适配1.2 弹性布局 2. 数据展示与交互2.1 数据卡片渲染2.2 图表区域 3. 事件处理机制3.1 点击事件处理3.2 手势…...

mysql进阶(三)
MySQL架构和存储引擎 1. MySQL架构 MySQL8.0服务器是由连接池、服务管理⼯具和公共组件、NoSQL接⼝、SQL接⼝、解析器、优化 器、缓存、存储引擎、⽂件系统组成。MySQL还为各种编程语⾔提供了⼀套⽤于外部程序访问服务器 的连接器。整体架构图如下所⽰: 2. 连接层 …...

MySQL 架构、索引优化、DDL解析、死锁排查
私人博客传送门 MySQL 认识索引 | 魔筝炼药师 MySQL 索引优化 | 魔筝炼药师 OnlineDDL(在 MySQL 5.7 数据库里,InnoDB引擎,执行一条DDL会发生什么事情) | 魔筝炼药师 MySQL 死锁排查 | 魔筝炼药师...
AVM 环视拼接 鱼眼相机
https://zhuanlan.zhihu.com/p/651306620 AVM 环视拼接方法介绍 从内外参推导IPM变换方程及代码实现(生成AVM环视拼接图)_avm拼接-CSDN博客 经典文献阅读之--Extrinsic Self-calibration of the Surround-view System: A Weakly... (环视系统的外参自…...

【Flink银行反欺诈系统设计方案】5.反欺诈系统全生命周期设计
【Flink银行反欺诈系统设计方案】反欺诈系统全生命周期设计 概要:1. 事前反欺诈准备核心模块与架构: 2. 事中反欺诈发现与告警核心模块与架构: 3. 事后反欺诈事件分析核心模块与架构: 4. 反欺诈闭环架构设计整体技术栈:…...
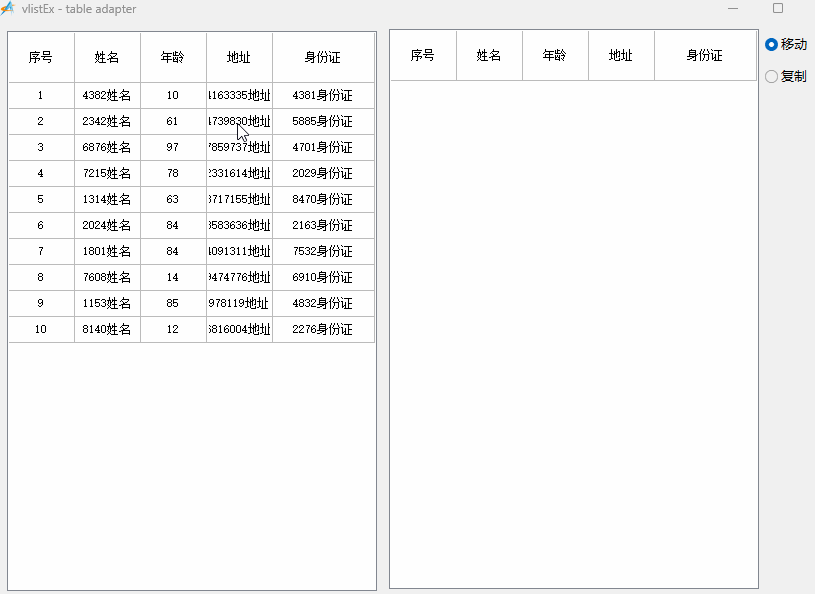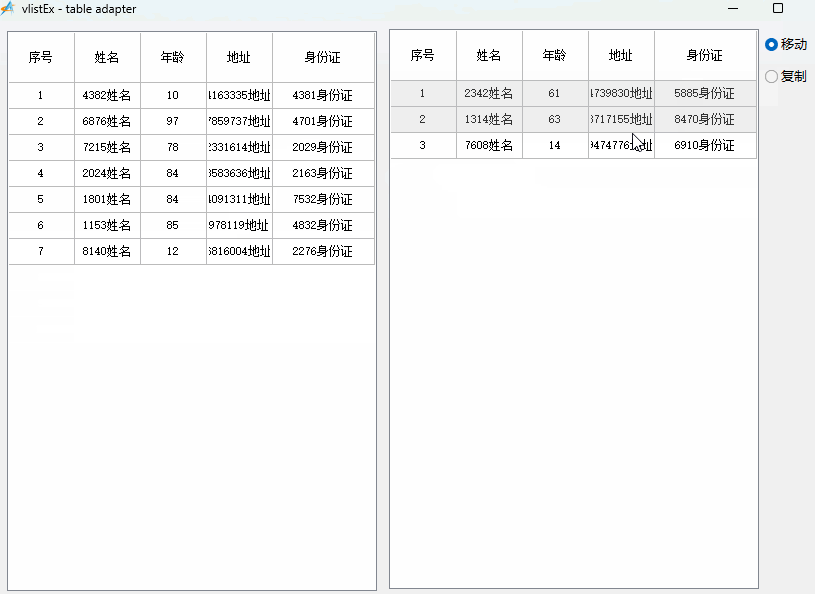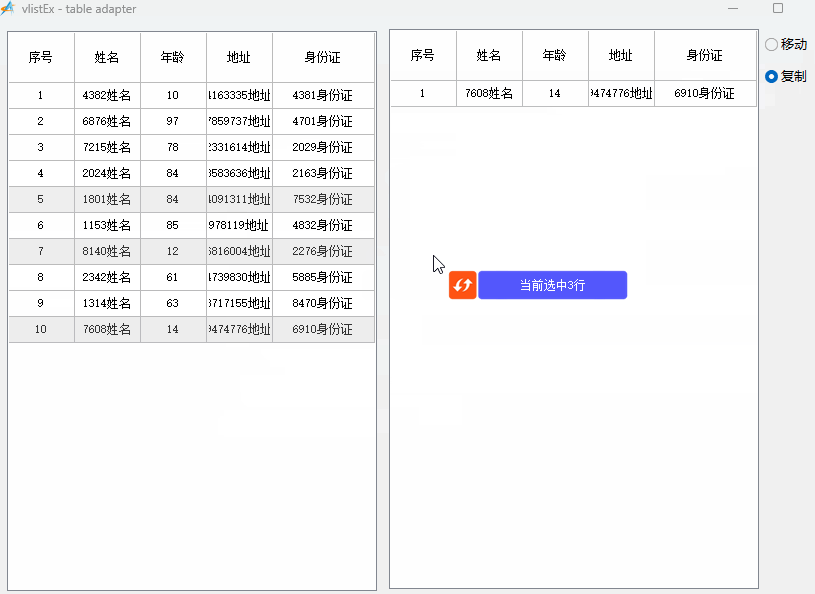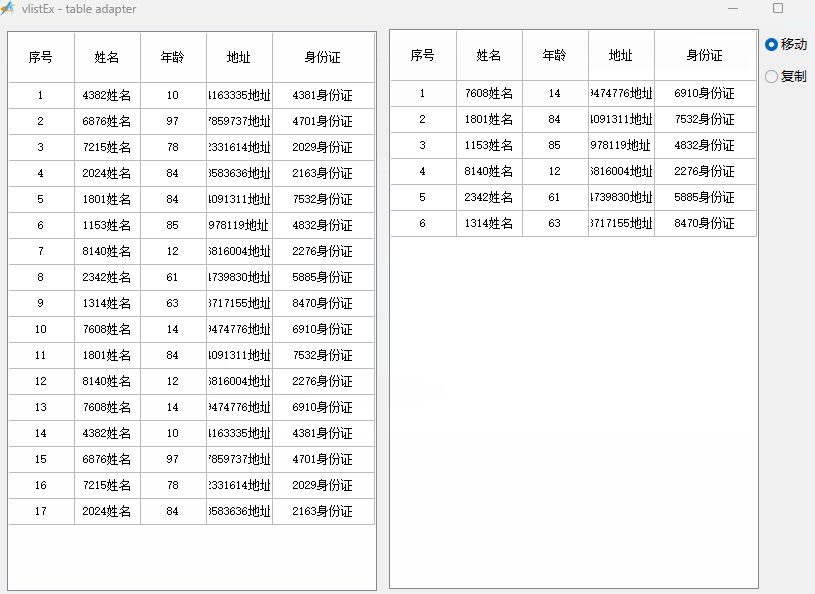
aardio - 虚表 —— 两个虚表之间互相拖动交换数据
插入到虚表末尾的方法: import win.ui; import godking.vlistEx; /*DSG{{*/ mainForm win.form(text"vlistEx - table adapter";right849;bottom578;border"thin") mainForm.add( radiobutton{cls"radiobutton";text"移动&qu…...
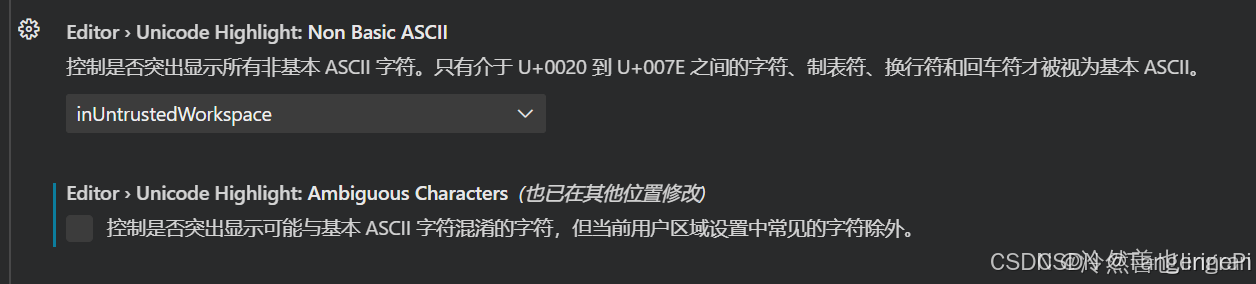
VScode 中文符号出现黄色方框的解决方法
VScode 中文符号出现黄色方框的解决方法 我的vscode的python多行注释中会将中文字符用黄色方框框处: 只需要打开设置搜索unicode,然后将这一项的勾选取消掉就可以了: 取消之后的效果如下: 另一种情况:中文显示出现黄色…...
LINUX网络基础 [二] - 网络编程套接字,UDP与TCP
目录 前言 一. 端口号的认识 1.1 端口号的作用 二. 初识TCP协议和UDP协议 2.1 TCP协议 TCP的特点 使用场景 2.2 UDP协议 UDP的特点 使用场景 2.3 TCP与UDP的对比 2.4 思考 2.5 总结 三. 网络字节序 3.1 网络字节序的介绍 3.2 网络字节序思考 四. socket接口 …...
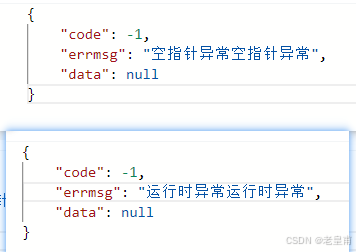
Spring统一格式返回
目录 一:统一结果返回 1:统一结果返回写法 2:String类型报错问题 解决方法 二:统一异常返回 统一异常返回写法 三:总结 同志们,今天咱来讲一讲统一格式返回啊,也是好久没有讲过统一格式返…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...






