每日一题——搜索二维矩阵
搜索二维矩阵
- 一、题目背景
- 二、题目描述
- 示例 1:
- 示例 2:
- 约束条件:
- 三、解题思路分析
- 1. **错误思路回顾**
- 2. **Z字形查找算法**
- 算法步骤:
- 3. **算法优势**
- 四、代码实现
- 代码说明:
- 五、测试用例
- 测试用例 1:
- 测试用例 2:
- 测试用例 3:
- 六、总结
一、题目背景
在LeetCode上,有一道经典的二维矩阵搜索问题——“搜索二维矩阵 II”。题目要求在一个具有特定性质的二维矩阵中查找目标值。矩阵的每一行从左到右升序排列,每一列从上到下升序排列。我们需要设计一个高效的算法来判断目标值是否存在于矩阵中。
二、题目描述
给定一个二维矩阵matrix和一个目标值target,矩阵的行数为m,列数为n。矩阵满足以下性质:
- 每一行的元素从左到右升序排列。
- 每一列的元素从上到下升序排列。
我们需要判断目标值target是否存在于矩阵中。
示例 1:
输入:
matrix = [[1, 4, 7, 11, 15],[2, 5, 8, 12, 19],[3, 6, 9, 16, 22],[10, 13, 14, 17, 24],[18, 21, 23, 26, 30]
]
target = 5
输出:true
示例 2:
输入:
matrix = [[1, 4, 7, 11, 15],[2, 5, 8, 12, 19],[3, 6, 9, 16, 22],[10, 13, 14, 17, 24],[18, 21, 23, 26, 30]
]
target = 20
输出:false
约束条件:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 300-10^9 <= matrix[i][j] <= 10^9- 每一行的所有元素从左到右升序排列
- 每一列的所有元素从上到下升序排列
-10^9 <= target <= 10^9
三、解题思路分析
1. 错误思路回顾
在解题过程中,我们可能会尝试一些直观的思路,但这些方法往往效率低下或存在逻辑错误。例如,从矩阵的左上角开始逐行逐列搜索,或者在矩阵中随机选择一个起点进行搜索。这些方法的时间复杂度较高,无法满足题目对效率的要求。
2. Z字形查找算法
经过分析,我们发现一种高效的搜索方法——Z字形查找。这种方法利用了矩阵的有序性,从矩阵的右上角(或左下角)开始搜索,通过逐步调整搜索范围,快速定位目标值。
算法步骤:
- 初始化:从矩阵的右上角开始搜索,设当前坐标为
(x, y),其中x = 0,y = n - 1。 - 搜索过程:
- 如果
matrix[x][y] == target,说明找到了目标值,返回true。 - 如果
matrix[x][y] > target,由于每一列是升序排列的,当前列的所有元素都大于目标值,因此将y减1,即向左移动。 - 如果
matrix[x][y] < target,由于每一行是升序排列的,当前行的所有元素都小于目标值,因此将x加1,即向下移动。
- 如果
- 边界条件:如果搜索过程中超出矩阵的边界(
x >= m或y < 0),说明目标值不存在,返回false。
3. 算法优势
Z字形查找算法充分利用了矩阵的有序性,避免了不必要的搜索。其时间复杂度为O(m + n),其中m是矩阵的行数,n是矩阵的列数。相比暴力搜索(时间复杂度为O(m * n)),这种方法效率显著提高。
四、代码实现
以下是基于Z字形查找算法的C语言实现:
bool searchMatrix(int** matrix, int matrixSize, int* matrixColSize, int target) {int m = matrixSize; // 矩阵的行数int n = *matrixColSize; // 矩阵的列数int x = 0, y = n - 1; // 从右上角开始搜索while (x < m && y >= 0) { // 确保搜索范围在矩阵内if (matrix[x][y] == target) { // 找到目标值return true;} else if (matrix[x][y] > target) { // 当前值大于目标值,向左移动y--;} else { // 当前值小于目标值,向下移动x++;}}return false; // 超出矩阵边界,目标值不存在
}
代码说明:
- 初始化:
x为0,y为矩阵的列数减1,即从右上角开始。 - 循环条件:
x < m且y >= 0,确保搜索范围在矩阵内。 - 搜索逻辑:
- 如果当前值等于目标值,直接返回
true。 - 如果当前值大于目标值,向左移动(
y--)。 - 如果当前值小于目标值,向下移动(
x++)。
- 如果当前值等于目标值,直接返回
- 返回结果:如果超出矩阵边界仍未找到目标值,返回
false。
五、测试用例
测试用例 1:
matrix = [[1, 4, 7, 11, 15],[2, 5, 8, 12, 19],[3, 6, 9, 16, 22],[10, 13, 14, 17, 24],[18, 21, 23, 26, 30]
]
target = 5
输出:true
测试用例 2:
matrix = [[1, 4, 7, 11, 15],[2, 5, 8, 12, 19],[3, 6, 9, 16, 22],[10, 13, 14, 17, 24],[18, 21, 23, 26, 30]
]
target = 20
输出:false
测试用例 3:
matrix = [[1, 2, 3],[4, 5, 6],[7, 8, 9]
]
target = 7
输出:true
六、总结
通过Z字形查找算法,我们能够高效地解决“搜索二维矩阵 II”问题。这种方法充分利用了矩阵的有序性,避免了暴力搜索的低效性。在实际应用中,我们还可以根据矩阵的性质选择其他优化策略,例如从左下角开始搜索,逻辑与从右上角类似。
这题本质上就是从右上角往右下角遍历,还是比较容易的。
相关文章:

每日一题——搜索二维矩阵
搜索二维矩阵 一、题目背景二、题目描述示例 1:示例 2:约束条件: 三、解题思路分析1. **错误思路回顾**2. **Z字形查找算法**算法步骤: 3. **算法优势** 四、代码实现代码说明: 五、测试用例测试用例 1:测试…...

PPT 小黑第21套
对应大猫22 动作按钮 “转到首页” 编号从1开始显示,点设计 -幻灯片大小 -修改幻灯片编号起始值为0(那么第二张幻灯片页码为1)...

大模型day01自然语言+大模型+环境
[TOC]大模型day01 自然语言处理 汉字的词是连着的,所以需要一个汉语处理模块,把词语、成语自动加空格隔开。 知识图谱构建——>从大语言文本挖掘出来 自然语言处理:翻译、智能语音 自然语言处理:理解一句话意思,…...
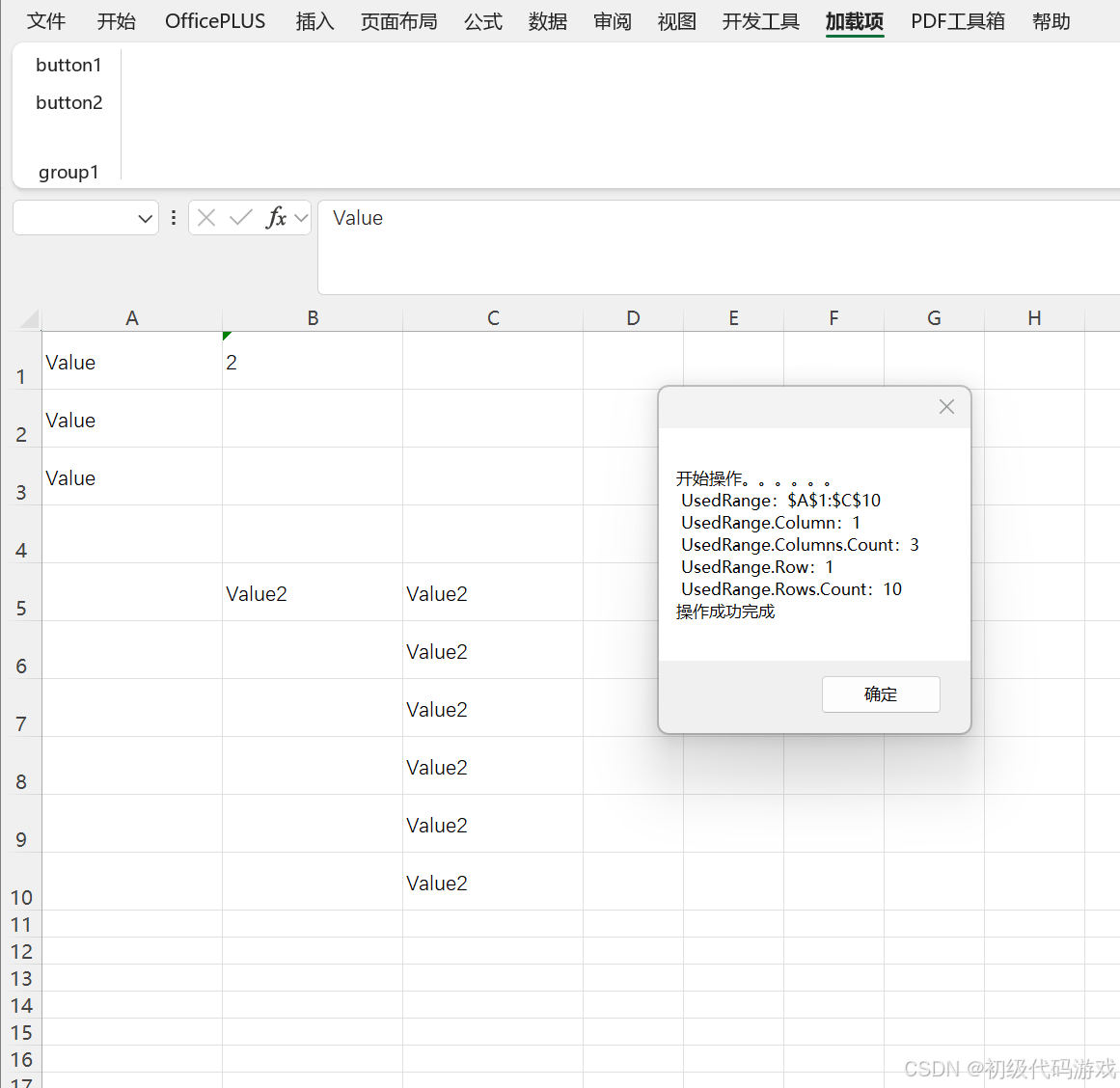
VSTO(C#)Excel开发3:Range对象 处理列宽和行高
初级代码游戏的专栏介绍与文章目录-CSDN博客 我的github:codetoys,所有代码都将会位于ctfc库中。已经放入库中我会指出在库中的位置。 这些代码大部分以Linux为目标但部分代码是纯C的,可以在任何平台上使用。 源码指引:github源…...

【2025】Electron + React 架构筑基——从零到一的跨平台开发
引言 源代码仓库: Github仓库【electron_git】 你是否厌倦了在命令行中反复输入git status,却依然无法直观看到文件变化? 是否羡慕VS Code的丝滑Git集成,却苦恼于无法定制自己的专属工具? 本专栏将为你打开一扇新的…...

AWS 如何导入内部SSL 证书
SSL 证书的很重要的功能就是 HTTP- > HTTPS, 下面就说明一下怎么导入ssl 证书,然后绑定证书到ALB. 以下示例说明如何使用 AWS Management Console 导入证书。 从以下位置打开 ACM 控制台:https://console.aws.amazon.com/acm/home。如果您是首次使用 ACM,请查找 AWS Cer…...

清华北大推出的 DeepSeek 教程(附 PDF 下载链接)
清华和北大分别都有关于DeepSeek的分享文档,内容非常全面,从原理和具体的应用,大家可以认真看看。 北大 DeepSeek 系列 1:提示词工程和落地场景.pdf 北大 DeepSeek 系列 2:DeepSeek 与 AIGC 应用.pdf 清华 Deep…...

【空地协同技术教程:概念与技术手段解析】
空地协同技术教程:概念与技术手段解析 一、空地协同的概念与核心价值 定义 空地协同(Air-Ground Collaboration)是指通过无人机(UAV)与无人车(UGV)等异构平台的跨域协作,利用各自的…...

【2025小黑课堂】计算机二级WPS精选系列20G内容(可下载:真题+预测卷+软件+选择题)
2025年3月全国计算机等级考试即将于3月29日至31日举行。为了帮助广大考生高效备考,小编特意收集并整理了最新版(备考2025年3月)的小黑课堂计算机二级WPS 电脑题库软件,助力考生在考试中游刃有余,轻松通关! …...

蓝桥杯备赛:炮弹
题目解析 这道题目是一道模拟加调和级数,难的就是调和级数,模拟过程比较简单。 做法 这道题目的难点在于我们在玩这个跳的过程,可能出现来回跳的情况,那么为了解决这种情况,我们采取的方法是设定其的上限步数。那么…...

kotlin高级用法总结
Kotlin 是一门功能强大且灵活的编程语言,除了基础语法外,它还提供了许多高级特性,可以帮助你编写更简洁、高效和可维护的代码。以下是 Kotlin 的一些高级用法,涵盖了协程、扩展函数、属性委托、内联类、反射等内容。 协程&#x…...

transformers - AWQ
本文翻译整理自:https://huggingface.co/docs/transformers/main/en/quantization/awq 文章目录 一、引言二、加载 autoawq 量化的模型三、Fused modules支持的架构不受支持的架构 四、ExLlamaV2五、CPU 一、引言 Activation-aware Weight Quantization (AWQ) 激活…...

mysql下载与安装、关系数据库和表的创建
一、mysql下载: MySQL获取: 官网:www.mysql.com 也可以从Oracle官方进入:https://www.oracle.com/ 下载地址:https://downloads.mysql.com/archives/community/ 选择对应的版本和对应的操作系统ÿ…...

在华为设备上,VRRP与BFD结合使用可以快速检测链路故障并触发主备切换
在华为设备上,VRRP与BFD结合使用可以快速检测链路故障并触发主备切换。以下是VLAN接口下配置VRRP与BFD的步骤: 目录 1. 配置BFD会话 2. 配置VLAN接口 3. 配置VRRP 4. 验证配置 5. 保存配置 1. 配置BFD会话 在两台设备之间配置BFD会话,…...

RK3588开发笔记-fiq_debugger: cpu 0 not responding, reverting to cpu 3问题解决
目录 前言 一、FIQ Debugger介绍 二、rockchip平台配置方法 三、问题分析定位 IRQF_NOBALANCING 的含义 总结 前言 在进行 RK3588 开发的过程中,我们可能会遇到各种棘手的问题。其中,“fiq_debugger: cpu 0 not responding, reverting to cpu 3” 这个错误出现在RK3588的…...

新能源汽车充电综合解决方案:安科瑞电气助力绿色出行
安科瑞 华楠 18706163979 随着新能源汽车的迅猛发展,充电基础设施的建设成为了推动行业进步的关键。然而,充电技术滞后、运营效率低下、车桩比失衡等问题,依然困扰着广大车主和运营商。今天,我们要为大家介绍一款新能源汽车充电…...

大语言模型进化论:从达尔文到AI的启示与展望
文章大纲 引言大语言模型中的“进化论”思想体现遗传变异过度繁殖和生存斗争大模型“过度繁殖”与“生存竞争”机制解析**一、过度繁殖:技术迭代的指数级爆发****二、生存竞争:计算资源的达尔文战场****三、生存竞争胜出关键要素****四、行业竞争格局演化趋势**核心结论自然选…...

Spring Boot与Axon Framework整合教程
精心整理了最新的面试资料和简历模板,有需要的可以自行获取 点击前往百度网盘获取 点击前往夸克网盘获取 简介 Axon Framework是一个用于构建CQRS(命令查询职责分离)和事件溯源(Event Sourcing)应用的框架࿰…...

深度学习Dropout
一、概念 Dropout是为了解决过拟合,当层数加深,就有可能过拟合,这个时候模型太复杂就会过拟合,那么可以让模型变得简单一点,所以就可以随机挑一些神经元,让某些神经元的输出是0,只保留部分神经…...

2025华为OD机试真题E卷 - 螺旋数字矩阵【Java】
题目描述 疫情期间,小明隔离在家,百无聊赖,在纸上写数字玩。他发明了一种写法:给出数字个数 n (0 < n ≤ 999)和行数 m(0 < m ≤ 999),从左上角的 1 开始,按照顺时针螺旋向内写方式,依次写出2,3,…,n,最终形成一个 m 行矩阵。小明对这个矩阵有些要求: 1、…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

ubuntu系统文件误删(/lib/x86_64-linux-gnu/libc.so.6)修复方案 [成功解决]
报错信息:libc.so.6: cannot open shared object file: No such file or directory: #ls, ln, sudo...命令都不能用 error while loading shared libraries: libc.so.6: cannot open shared object file: No such file or directory重启后报错信息&…...

人工智能 - 在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型
在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型。这些平台各有侧重,适用场景差异显著。下面我将从核心功能定位、典型应用场景、真实体验痛点、选型决策关键点进行拆解,并提供具体场景下的推荐方案。 一、核心功能定位速览 平台核心定位技术栈亮…...

2025-05-08-deepseek本地化部署
title: 2025-05-08-deepseek 本地化部署 tags: 深度学习 程序开发 2025-05-08-deepseek 本地化部署 参考博客 本地部署 DeepSeek:小白也能轻松搞定! 如何给本地部署的 DeepSeek 投喂数据,让他更懂你 [实验目的]:理解系统架构与原…...
