蓝桥杯备赛:炮弹

题目解析
这道题目是一道模拟加调和级数,难的就是调和级数,模拟过程比较简单。
做法
这道题目的难点在于我们在玩这个跳的过程,可能出现来回跳的情况,那么为了解决这种情况,我们采取的方法是设定其的上限步数。那么怎么确定其的上限步数呢?(刚开始我也没想到怎么去确定,听了y总的讲解后大悟还可以这样玩。)我们可以想情况要么它就是中间都是1步,从最左边到最右边,然后又从最右边到最左边(极限情况),如果这时候再从最左边往右肯定就是超了,那么其的步数就是2*N/1。但是它中间也有可能是2步或者3步,这里我们也要去取极限。那么最终的最大的步数就是2N/1+2N/2+…+2N/N。那么其实有很多人不理解为什么要这样折腾,只弄一次的不就好了吗,这里我给大家画个图大家就能明白了。

那么其实我们是在对每一种情况去取极限,防止它超。
那么我们来计算一下最大步数。

这里面设计到调和级数的计算,大家可以看一下数学

那么我们这里的估计是24N,我们可以再往上取一点,因为我们这里忽略了0.577,那么就是26N左右。
#include<iostream>
using namespace std;
const int N=1e6;
int q[N],b[N];//q记录是炮弹还是板,b记录炮弹和反板的数值
bool st[N];//记录每个状态
int main()
{int n,x;cin>>n>>x;for(int i=1;i<=n;i++)cin>>q[i]>>b[i];//int cnt=0,ans=0,d=1,m=1;//cnt记录步数,d是方向,m是能量`while(cnt<26*n){if(q[x])//如果是炮弹{if(!st[x]&&m>=b[x]){st[x]=true;//标记一下,这里的炮弹被击破ans++;}}else{d=-d;//改变方向m+=b[x];//能量改变}x+=m*d;//移动if(x<=0||x>n)break;cnt++;}cout<<ans;return 0;
}
相关文章:

蓝桥杯备赛:炮弹
题目解析 这道题目是一道模拟加调和级数,难的就是调和级数,模拟过程比较简单。 做法 这道题目的难点在于我们在玩这个跳的过程,可能出现来回跳的情况,那么为了解决这种情况,我们采取的方法是设定其的上限步数。那么…...

kotlin高级用法总结
Kotlin 是一门功能强大且灵活的编程语言,除了基础语法外,它还提供了许多高级特性,可以帮助你编写更简洁、高效和可维护的代码。以下是 Kotlin 的一些高级用法,涵盖了协程、扩展函数、属性委托、内联类、反射等内容。 协程&#x…...

transformers - AWQ
本文翻译整理自:https://huggingface.co/docs/transformers/main/en/quantization/awq 文章目录 一、引言二、加载 autoawq 量化的模型三、Fused modules支持的架构不受支持的架构 四、ExLlamaV2五、CPU 一、引言 Activation-aware Weight Quantization (AWQ) 激活…...

mysql下载与安装、关系数据库和表的创建
一、mysql下载: MySQL获取: 官网:www.mysql.com 也可以从Oracle官方进入:https://www.oracle.com/ 下载地址:https://downloads.mysql.com/archives/community/ 选择对应的版本和对应的操作系统ÿ…...

在华为设备上,VRRP与BFD结合使用可以快速检测链路故障并触发主备切换
在华为设备上,VRRP与BFD结合使用可以快速检测链路故障并触发主备切换。以下是VLAN接口下配置VRRP与BFD的步骤: 目录 1. 配置BFD会话 2. 配置VLAN接口 3. 配置VRRP 4. 验证配置 5. 保存配置 1. 配置BFD会话 在两台设备之间配置BFD会话,…...

RK3588开发笔记-fiq_debugger: cpu 0 not responding, reverting to cpu 3问题解决
目录 前言 一、FIQ Debugger介绍 二、rockchip平台配置方法 三、问题分析定位 IRQF_NOBALANCING 的含义 总结 前言 在进行 RK3588 开发的过程中,我们可能会遇到各种棘手的问题。其中,“fiq_debugger: cpu 0 not responding, reverting to cpu 3” 这个错误出现在RK3588的…...

新能源汽车充电综合解决方案:安科瑞电气助力绿色出行
安科瑞 华楠 18706163979 随着新能源汽车的迅猛发展,充电基础设施的建设成为了推动行业进步的关键。然而,充电技术滞后、运营效率低下、车桩比失衡等问题,依然困扰着广大车主和运营商。今天,我们要为大家介绍一款新能源汽车充电…...

大语言模型进化论:从达尔文到AI的启示与展望
文章大纲 引言大语言模型中的“进化论”思想体现遗传变异过度繁殖和生存斗争大模型“过度繁殖”与“生存竞争”机制解析**一、过度繁殖:技术迭代的指数级爆发****二、生存竞争:计算资源的达尔文战场****三、生存竞争胜出关键要素****四、行业竞争格局演化趋势**核心结论自然选…...

Spring Boot与Axon Framework整合教程
精心整理了最新的面试资料和简历模板,有需要的可以自行获取 点击前往百度网盘获取 点击前往夸克网盘获取 简介 Axon Framework是一个用于构建CQRS(命令查询职责分离)和事件溯源(Event Sourcing)应用的框架࿰…...

深度学习Dropout
一、概念 Dropout是为了解决过拟合,当层数加深,就有可能过拟合,这个时候模型太复杂就会过拟合,那么可以让模型变得简单一点,所以就可以随机挑一些神经元,让某些神经元的输出是0,只保留部分神经…...

2025华为OD机试真题E卷 - 螺旋数字矩阵【Java】
题目描述 疫情期间,小明隔离在家,百无聊赖,在纸上写数字玩。他发明了一种写法:给出数字个数 n (0 < n ≤ 999)和行数 m(0 < m ≤ 999),从左上角的 1 开始,按照顺时针螺旋向内写方式,依次写出2,3,…,n,最终形成一个 m 行矩阵。小明对这个矩阵有些要求: 1、…...

DeepSeek 助力 Vue3 开发:打造丝滑的表格(Table)示例3: 行选择
前言:哈喽,大家好,今天给大家分享一篇文章!并提供具体代码帮助大家深入理解,彻底掌握!创作不易,如果能帮助到大家或者给大家一些灵感和启发,欢迎收藏关注哦 💕 目录 Deep…...
)
Linux驱动开发(1.基础创建)
序言:从高层逻辑到底层硬件的回归 在当今的软件开发中,我们习惯于用高级语言构建抽象层——通过框架、库和云服务快速实现功能。这种“软逻辑”的便利性让开发效率倍增,却也逐渐模糊了我们对计算机本质的认知:一切代码终将落地为…...

mmseg
系列文章目录 文章目录 系列文章目录bug bug File "/public/home/rsinfo/project/mmsegmentation/mmseg/__init__.py", line 61, in <module>assert (mmcv_min_version < mmcv_version < mmcv_max_version), \ AssertionError: MMCV2.2.0 is used but i…...

LangChain核心概念
下面整理的LangChain部分核心概念: 聊天模型【Chat models】:通过聊天 API 暴露的大语言模型(LLMs),将消息序列作为输入,并输出一条消息。消息【Messages】:聊天模型中的通信单元,…...

阿里巴巴全新推理模型QwQ-32B:性能比肩DeepSeek-R1,开源引领未来
摘要 阿里巴巴集团于深夜正式发布全新推理模型QwQ-32B,其性能与DeepSeek-R1完整版相当。该模型已通过Apache 2.0开源协议在Hugging Face和ModelScope平台发布。用户可通过Qwen Chat平台直接体验QwQ-32B的强大功能。这一举措不仅展示了阿里巴巴在人工智能领域的技术实…...

使用Arduino和ESP8266进行基于物联网的垃圾箱监控
使用 Arduino 和 ESP8266 的基于 IOT 的垃圾箱监控系统 在这个 DIY 中,我们将制作一个基于 IOT 的垃圾箱/垃圾监控系统,该系统将通过网络服务器告诉我们垃圾桶是空的还是满的,并且您可以通过互联网从世界任何地方了解“垃圾桶”或“垃圾箱”的状态。它将非常有用,可以安装…...
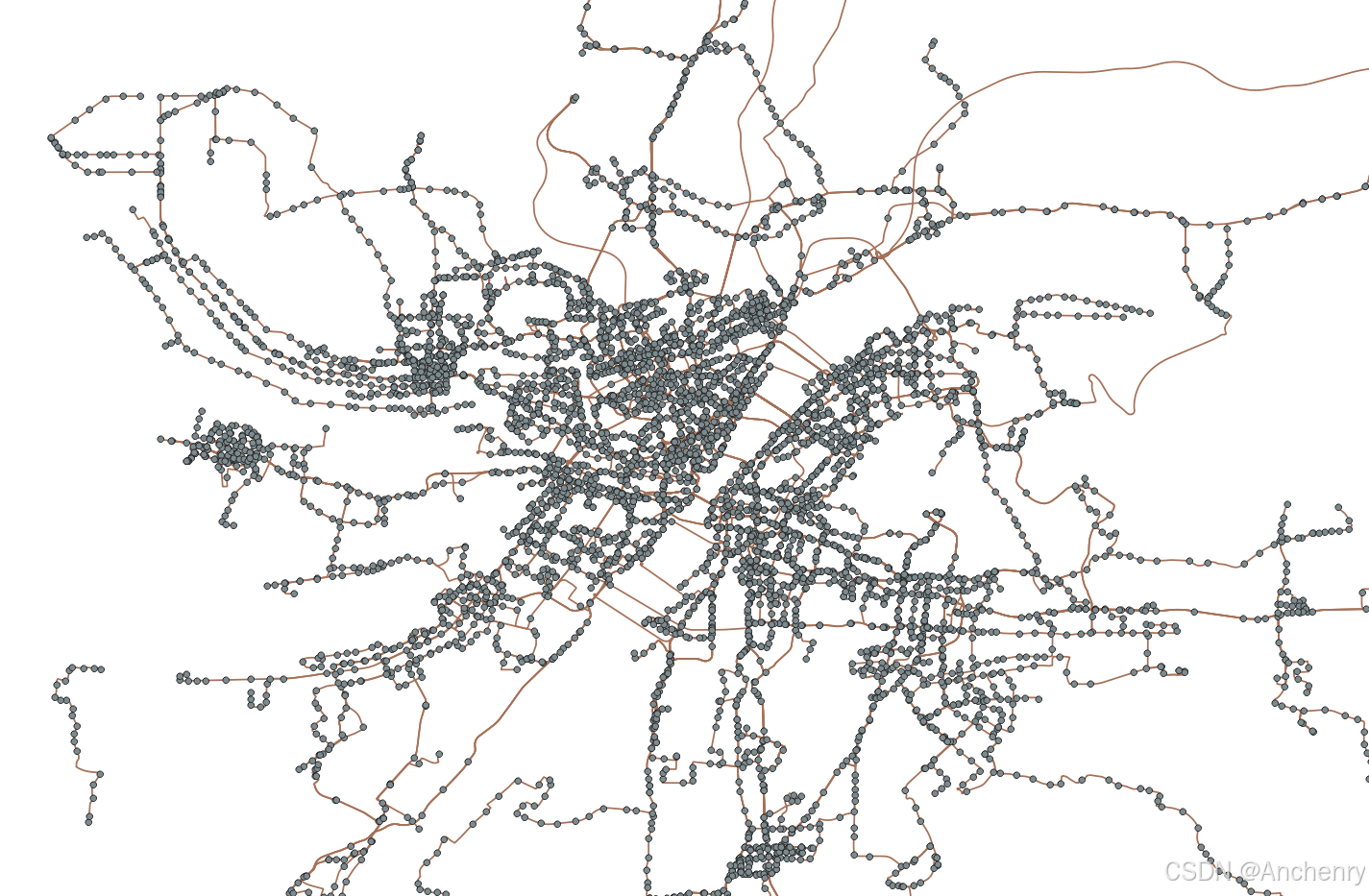
【Python爬虫】爬取公共交通路网数据
程序来自于Github,以下这篇博客作为完整的学习记录,也callback上一篇爬取公共交通站点的博文。 Bardbo/get_bus_lines_and_stations_data_from_gaode: 这个项目是基于高德开放平台和公交网获取公交线路及站点数据,并生成shp文件,…...

基于Matlab的人脸识别的二维PCA
一、基本原理 传统 PCA 在处理图像数据时,需将二维图像矩阵拉伸为一维向量,这使得数据维度剧增,引发高计算成本与存储压力。与之不同,2DPCA 直接基于二维图像矩阵展开运算。 它着眼于图像矩阵的列向量,构建协方差矩阵…...

SSM架构 +Nginx+FFmpeg实现rtsp流转hls流,在前端html上实现视频播放
序言: 本文介绍通过SSM架构 NginxFFmpeg实现rtsp流转hls流,在前端html上实现视频播放功能。此方法可用于网络摄像头RTSP视频流WEB端实时播放。(海康和大华都可以),我使用的是海康 步骤一:安装软件 FFmpeg…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...
