相机几何:从三维世界到二维图像的映射
本系列课程将带领读者开启一场独特的三维视觉工程之旅。我们不再止步于教科书式的公式推导,而是聚焦于如何将抽象的数学原理转化为可落地的工程实践。通过解剖相机的光学特性、构建成像数学模型、解析坐标系转换链条,直至亲手实现参数标定代码,我们将层层剥开三维视觉系统的核心构造。
在这场旅程中,您将理解为何简单的针孔模型能衍生出自动驾驶的感知算法,掌握透镜畸变参数如何影响AR眼镜的虚实配准精度,洞悉坐标系转换矩阵怎样支撑工业机器人的空间定位。我们特别设计了"理论-建模-代码"三位一体的讲解框架,使三维重建的数学原理真正可编程、可调试、可优化。
第一章:相机几何与标定——为什么我们需要关注它?
想象一下,你正在用手机拍摄一张照片。你按下快门,咔嚓一声,一张美丽的风景照就诞生了。但你知道吗?在这看似简单的动作背后,隐藏着一个复杂的数学世界——相机几何。它就像是一把钥匙,帮我们打开从三维世界到二维图像的神秘之门。
1. 相机几何:从三维到二维的魔法

1.1 为什么我们需要相机几何?
我们生活在一个三维的世界里,但相机拍出来的照片却是二维的。那么,相机是如何把立体的世界“压扁”成平面的呢?这就是相机几何要解决的问题。
-
针孔相机的启示:
想象一个小黑屋,墙上开了一个小孔,外面的光线通过这个小孔在屋内形成倒立的图像。这就是最简单的相机模型——针孔相机。它告诉我们,光线通过一个点(小孔)可以在平面上形成图像。 -
透镜的加入:
但针孔相机有个问题:图像太暗了!于是,我们加入了透镜。透镜就像是一个魔法师,它能把更多的光线聚焦到成像平面上,让图像变得更亮。但魔法师也有自己的脾气——它引入了畸变和失焦等问题。
1.2 相机几何的作用
相机几何的核心任务就是描述三维世界中的点如何映射到二维图像上。它帮我们回答以下问题:
- 为什么远处的物体看起来更小?
- 为什么平行的铁轨在照片中会相交?
- 为什么我的照片边缘会变形?
2. 相机标定:相机的“体检报告”
2.1 什么是相机标定?
相机标定就像是给相机做一次全面的体检。我们需要知道相机的“健康状况”——它的焦距、主点位置、畸变参数等。这些参数决定了相机如何“看”世界。
2.2 为什么我们需要相机标定?
-
精确建模:
如果你想让机器人用相机测量物体的距离,或者让无人机用相机导航,你必须知道相机的内部参数。否则,机器人可能会把1米误认为2米,无人机可能会撞墙。 -
消除畸变:
透镜会引入畸变,让直线变弯。通过标定,我们可以校正这些畸变,让图像更真实。 -
多相机协同:
在VR、AR或者电影特效中,常常需要多个相机协同工作。只有通过标定,才能确保这些相机“看”到的是同一个世界。
3. 相机几何与标定的应用场景
3.1 三维重建
通过多张照片,我们可以重建出三维场景。比如,考古学家可以用它重建古遗址,建筑师可以用它生成建筑物的三维模型。
3.2 自动驾驶
自动驾驶汽车依赖相机感知周围环境。通过相机几何,汽车可以计算其他车辆的距离和速度,避免碰撞。
3.3 虚拟现实(VR)与增强现实(AR)
在VR和AR中,相机几何帮我们精确地将虚拟物体叠加到现实世界中。比如,你可以在手机上看到虚拟的恐龙在你的房间里走来走去。
3.4 电影特效
在电影中,特效师用相机几何将CG角色无缝地融入实景拍摄中。比如,《阿凡达》中的潘多拉星球就是通过相机几何与现实场景完美结合的。
4. 总结:相机几何与标定——连接现实与数字的桥梁
相机几何与标定不仅仅是枯燥的数学公式,它是连接现实世界与数字世界的桥梁。无论是拍一张照片,还是让机器人自主导航,都离不开它。所以,下次当你按下快门时,不妨想一想:在这张照片背后,隐藏着一个多么神奇的数学世界
第二章 光圈,景深,焦距
1. 光圈(Aperture)

光圈是镜头中调节进光孔大小的装置,通常用f值表示,例如f/1.4、f/2.8、f/8等。光圈值越小,光圈越大,进光量越多;光圈值越大,光圈越小,进光量越少。光圈不仅控制进光量,还影响景深。大光圈(如f/1.4)会产生浅景深,背景虚化效果明显;小光圈(如f/16)则会产生深景深,背景和前景都较为清晰
2. 景深(Depth of Field, DOF)
景深是指照片中清晰成像的范围。景深的大小受光圈、焦距和拍摄距离的影响:
- 光圈:光圈越大(f值越小),景深越浅;光圈越小(f值越大),景深越深。
- 焦距:焦距越长,景深越浅;焦距越短,景深越深。
- 拍摄距离:拍摄距离越近,景深越浅;拍摄距离越远,景深越深。
景深的计算公式为:

其中,N是光圈值,c是容许弥散圆直径,m是放大倍率
3. 焦距(Focal Length)
焦距是指镜头中心到成像平面的距离,通常以毫米(mm)为单位。焦距决定了镜头的视角和放大倍率:
- 短焦距(如24mm):视角广,适合拍摄风景或大场景。
- 长焦距(如200mm):视角窄,适合拍摄远距离物体或特写。
焦距还影响景深,长焦距镜头更容易产生浅景深,而短焦距镜头则更容易产生深景深。
总结
- 光圈控制进光量和景深,大光圈适合拍摄人像,小光圈适合拍摄风景。
- 景深决定了照片中清晰的范围,受光圈、焦距和拍摄距离的影响。
- 焦距决定了镜头的视角和放大倍率,短焦距适合广角拍摄,长焦距适合远摄。
第三章:相机成像模型
相机成像模型是计算机视觉的基石,它描述了三维世界中的点如何映射到二维图像上。在这一章中,我们将从直观理解出发,逐步深入到数学公式,最后用Python代码实现一个简单的相机成像模型。
1. 针孔相机模型:最简单的成像原理
1.1 什么是针孔相机模型?
针孔相机模型是相机成像的最基础模型。它假设光线通过一个极小的孔(针孔)在成像平面上形成图像。
-
核心思想:
光线从物体上的某一点出发,通过针孔,最终在成像平面上形成一个点。所有点的集合就构成了完整的图像。 -
特点:
- 图像是倒立的
- 没有透镜,因此没有畸变
- 图像亮度较低(因为只有少量光线通过针孔)
1.2 数学建模
假设三维空间中的点 P=(X,Y,Z) 通过针孔相机投影到成像平面上的点 p=(x,y)。
根据相似三角形原理,可以得到:

其中,f 是焦距,表示针孔到成像平面的距离。
1.3 针孔相机的局限性
针孔相机局限性主要体现在以下几个方面,这些局限性不仅影响了其成像效果,也限制了其应用场景:
-
光圈限制:针孔相机的光圈大小受到针孔直径的限制,无法调节。这意味着在光线较暗的环境下,针孔相机需要更长的曝光时间,导致照片模糊。此外,小光圈也限制了相机的进光量,使得拍摄动态场景或高速运动物体时难以捕捉清晰的图像
- 分辨率限制:由于针孔的直径有限,针孔相机的分辨率相对较低,无法捕捉非常精细的图像细节。针孔直径越小,虽然成像的细节越清晰,但光线通过的数量也越少,需要更长的曝光时间。反之,针孔直径越大,光线通过的数量越多,但成像的细节就越模糊
-
无法实时调整:针孔相机无法进行实时调整,如调整焦距和光圈大小等参数。这使得拍摄者需要事先对光线和构图等方面进行充分的计算和准备,增加了拍摄的难度
-
衍射效应:当针孔直径过小时,光线通过针孔时会发生衍射现象,导致图像模糊。因此,针孔直径的选择需要在清晰度和进光量之间找到平衡。
2. 透镜的作用原理与机制
2.1 为什么需要透镜?
为了解决针孔相机图像太暗的问题,我们引入了透镜。透镜能够将更多的光线聚焦到成像平面上,从而提高图像的亮度。
2.2 透镜的基本原理
透镜通过折射改变光线的传播方向,使得从物体发出的光线能够汇聚到成像平面上的某一点。
-
焦点(Focal Point):
平行于光轴的光线通过透镜后会汇聚到一点,称为焦点。 -
焦距(Focal Length):
透镜中心到焦点的距离,记作 f。焦距决定了透镜的聚光能力和成像的大小。 -
成像公式:
透镜成像遵循以下公式:

-
其中,u 是物体到透镜的距离,v 是像到透镜的距离。
2.3 透镜带来的好处
- 提高亮度:透镜能够汇聚更多光线,使图像更亮。
- 选择性聚焦:通过调整透镜位置,可以选择性地聚焦在某个距离的物体上。
2.4. 透镜存在的问题
失焦(Defocus)

上图中红圈部分出现了失焦。当物体不在焦平面上时,成像会变得模糊。这是因为光线没有汇聚到同一个点,而是形成了一个光斑。
- 景深(Depth of Field):
能够清晰成像的物体距离范围。景深越大,能够清晰成像的物体距离范围越广。
径向畸变(Radial Distortion)
透镜的曲率会导致图像边缘的直线变弯,这种现象称为径向畸变。

上图中,左图为桶形畸变,右图为枕形畸变。
-
桶形畸变(Barrel Distortion):
图像边缘向内弯曲,像桶的形状。 -
枕形畸变(Pincushion Distortion):
图像边缘向外弯曲,像枕头的形状。 -
数学模型:
径向畸变可以用多项式模型来描述

2.5 色差(Chromatic Aberration)
不同波长的光通过透镜时折射率不同,导致颜色分离。这种现象称为色差。
第四章:坐标系转换——从三维世界到二维像素的数学与代码实现
1、为什么需要坐标系转换?
在计算机视觉和摄影测量中,相机的成像过程本质上是将三维世界中的物体映射到二维图像平面的过程。这一过程涉及多个坐标系的转换,原因如下:
- 视角适配:物体在世界坐标系中的位置是固定的,但相机的视角可能随时变化,需要通过坐标系转换描述物体在相机视角下的位置。
- 三维到二维映射:三维空间中的点需要投影到二维图像平面(如相机传感器)上,形成最终的像素坐标。
- 多传感器融合:在自动驾驶、机器人导航等场景中,不同传感器(如相机、激光雷达)的数据需要统一到同一坐标系中。
2、核心坐标系的定义与理解
2.1. 世界坐标系(World Coordinate System)
- 定义:描述物体在真实三维空间中的绝对位置,通常以场景中的某个固定点(如地面原点)为基准。
![]()
2.2. 相机坐标系(Camera Coordinate System)
- 定义:以相机光心为原点,光轴为Z轴,描述物体相对于相机的位置。
- 符号:Pc=(Xc,Yc,Zc)。
2.3. 图像坐标系(Image Coordinate System)
- 定义:以相机成像平面为中心,描述点在图像平面上的物理位置(单位为米)。
- 符号:pi=(x,y)。
2.4. 像素坐标系(Pixel Coordinate System)
- 定义:以图像左上角为原点,描述点在数字图像中的像素位置。
- 符号:pp=(u,v)。
3、坐标系转换的全过程
从世界坐标系到像素坐标系的转换分为三步,涉及刚体变换、透视投影和像素缩放。
3.1. 世界坐标系 → 相机坐标系(刚体变换)
数学公式:

- R:3×3旋转矩阵,描述相机姿态。
- t:3×1平移向量,描述相机位置。
代码实现:
import numpy as np# 世界坐标系中的点(齐次坐标)
P_w = np.array([2.0, 3.0, 5.0, 1.0]) # (X_w, Y_w, Z_w, 1)# 定义相机的旋转矩阵和平移向量
R = np.array([[1, 0, 0], [0, 1, 0], [0, 0, 1]]) # 无旋转
t = np.array([0, 0, 10]) # 相机沿Z轴平移10米# 构建刚体变换矩阵
T = np.eye(4)
T[:3, :3] = R
T[:3, 3] = t# 转换为相机坐标系
P_c = T @ P_w # 结果为齐次坐标 [X_c, Y_c, Z_c, 1]3.2. 相机坐标系 → 图像坐标系(透视投影)
数学公式:

# 相机内参矩阵(示例:焦距500像素,主点在图像中心)
K = np.array([[500, 0, 320],[0, 500, 240],[0, 0, 1]])# 提取相机坐标系中的点(非齐次坐标)
X_c, Y_c, Z_c = P_c[:3]# 透视投影到图像坐标系
x = (K[0,0] * X_c + K[0,1] * Y_c + K[0,2] * Z_c) / Z_c
y = (K[1,0] * X_c + K[1,1] * Y_c + K[1,2] * Z_c) / Z_c3.3. 图像坐标系 → 像素坐标系(物理尺寸缩放)
数学公式:

- dx,dy:单个像素的物理尺寸(例如0.001米/像素)。
# 假设像素物理尺寸为0.001米(即1毫米/像素)
dx, dy = 0.001, 0.001# 转换为像素坐标
u = x / dx + K[0,2] # K[0,2]是u_0
v = y / dy + K[1,2] # K[1,2]是v_0
print(f"像素坐标: ({u:.1f}, {v:.1f})")4、完整代码示例
import numpy as npdef world_to_pixel(P_w, R, t, K, dx=0.001, dy=0.001):"""将世界坐标系中的点转换到像素坐标系"""# 齐次坐标转换P_w_homogeneous = np.append(P_w, 1.0)# 刚体变换:世界坐标系 → 相机坐标系T = np.eye(4)T[:3, :3] = RT[:3, 3] = tP_c_homogeneous = T @ P_w_homogeneousX_c, Y_c, Z_c = P_c_homogeneous[:3]# 透视投影:相机坐标系 → 图像坐标系x = (K[0,0] * X_c + K[0,1] * Y_c + K[0,2] * Z_c) / Z_cy = (K[1,0] * X_c + K[1,1] * Y_c + K[1,2] * Z_c) / Z_c# 物理尺寸缩放:图像坐标系 → 像素坐标系u = x / dx + K[0,2]v = y / dy + K[1,2]return (u, v)# 示例参数
P_w = np.array([2.0, 3.0, 5.0]) # 世界坐标系中的点
R = np.eye(3) # 无旋转
t = np.array([0, 0, 10]) # 相机沿Z轴平移10米
K = np.array([[500, 0, 320],[0, 500, 240],[0, 0, 1]]) # 内参矩阵# 转换并输出结果
u, v = world_to_pixel(P_w, R, t, K)
print(f"世界坐标 {P_w} → 像素坐标 ({u:.1f}, {v:.1f})")5. 补充:图像坐标系到像素坐标系的深入解析
5.1、问题背景:为什么说“物理尺寸缩放”容易被误解?
在之前的坐标系转换流程中,图像坐标系到像素坐标系的转换被简化为以下公式:

其中 dx,dy 表示单个像素的物理尺寸(如0.001米/像素)。
这一步骤看似简单,但实际隐含了对相机内参矩阵 K 的深度理解。许多初学者会在此处混淆以下问题:
- 内参矩阵 K 中的 fx,fy 是否已包含像素物理尺寸?
- 为什么需要额外的 dx,dy 缩放?
- 主点偏移 u0,v0 的物理意义是什么?
以下将深入剖析这一过程。
5.2、内参矩阵 K 的物理意义
5.2.1. 内参矩阵的标准形式


5.3、修正后的转换流程
5.3.1. 相机坐标系 → 图像坐标系(物理单位:米)

此时 x物理,y物理 的单位为米。
5.3.2. 图像坐标系 → 像素坐标系(单位转换)

但这一步骤实际上已被内参矩阵 K 提前完成!
正确的做法是直接使用内参矩阵 K 一步到位:

5.3.3. 物理意义验证
假设相机参数如下:
- 物理焦距 f物理=0.05米(50毫米镜头)
- 像素尺寸 dx=dy=0.0001米(10微米/像素)
则内参矩阵应为:

与代码中的 K = [[500, 0, 320], [0, 500, 240]] 一致。此时:
- 世界点 (2,3,5) 在相机坐标系中为 (2,3,5−10)=(2,3,−5)(注意Z轴方向)。
- 投影到图像平面

但结果为负值,表明该点位于相机视野外。需调整参数确保 Zc>0。
5.4、常见问题解答
5.4.1. 为什么内参矩阵 K 能隐含像素物理尺寸?
因为 fx=f物理/dx,已通过焦距和像素尺寸的比值将物理单位转换为像素单位。
5.4.2. 何时需要显式使用 dx,dy?
仅在以下场景需要:
- 需要从像素坐标反推物理坐标(如三维重建)。
- 相机标定过程中计算内参矩阵 K。
5.4.3. 主点偏移 u0,v0 的实际意义?
- 表示光轴与图像平面的交点在像素坐标系中的位置。
- 对于理想相机,u0=图像宽度/2, v0=图像高度/2。
下一篇 : 相机的参数标定
相关文章:

相机几何:从三维世界到二维图像的映射
本系列课程将带领读者开启一场独特的三维视觉工程之旅。我们不再止步于教科书式的公式推导,而是聚焦于如何将抽象的数学原理转化为可落地的工程实践。通过解剖相机的光学特性、构建成像数学模型、解析坐标系转换链条,直至亲手实现参数标定代码࿰…...

【GoTeams】-5:引入Docker
本文目录 1. Dokcer-compose回顾下Docker知识编写docker-compose.yaml运行docker 2. 部署go服务编写dockerfile 1. Dokcer-compose 这里简单先用一下win版本的Docker,后期开发好了部署的时候再移植到服务器下进行docker部署。 输入命令docker-compose version 就可…...

基金股票期权期货投资方式对比
以下是基金、股票、期权和期货的详细对比分析,涵盖定义、核心特点、优势、劣势、适用场景及相互区别: 一、基金 定义 基金是通过集合投资者的资金,由专业管理人(基金经理)进行多元化投资的金融工具。根据投资标的可分…...
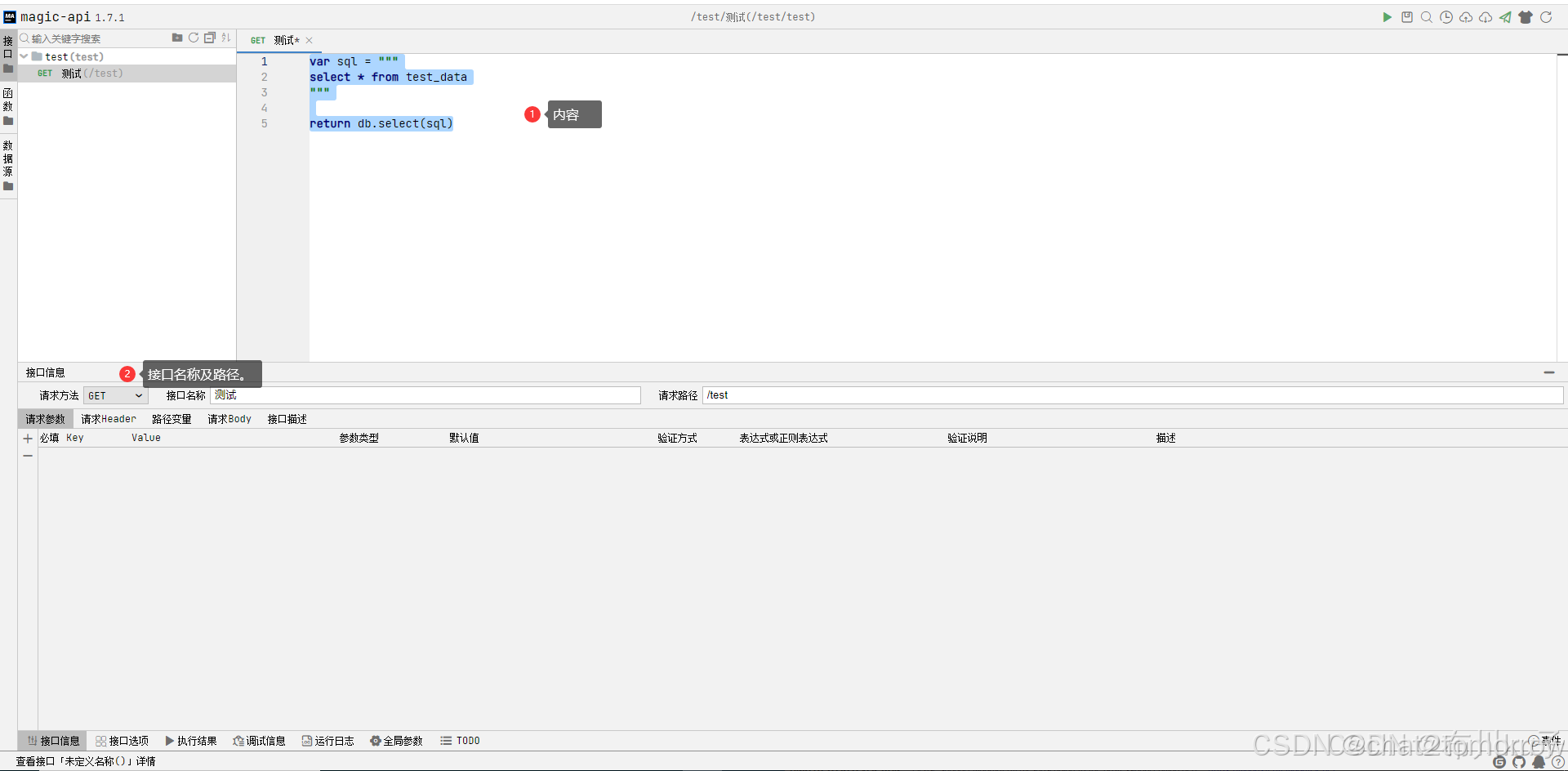
大模型AI平台DeepSeek 眼中的SQL2API平台:QuickAPI、dbapi 和 Magic API 介绍与对比
目录 1 QuickAPI 介绍 2 dbapi 介绍 3 Magic API 介绍 4 简单对比 5 总结 统一数据服务平台是一种低代码的方式,实现一般是通过SQL能直接生成数据API,同时能对产生的数据API进行全生命周期的管理,典型的SQL2API的实现模式。 以下是针对…...
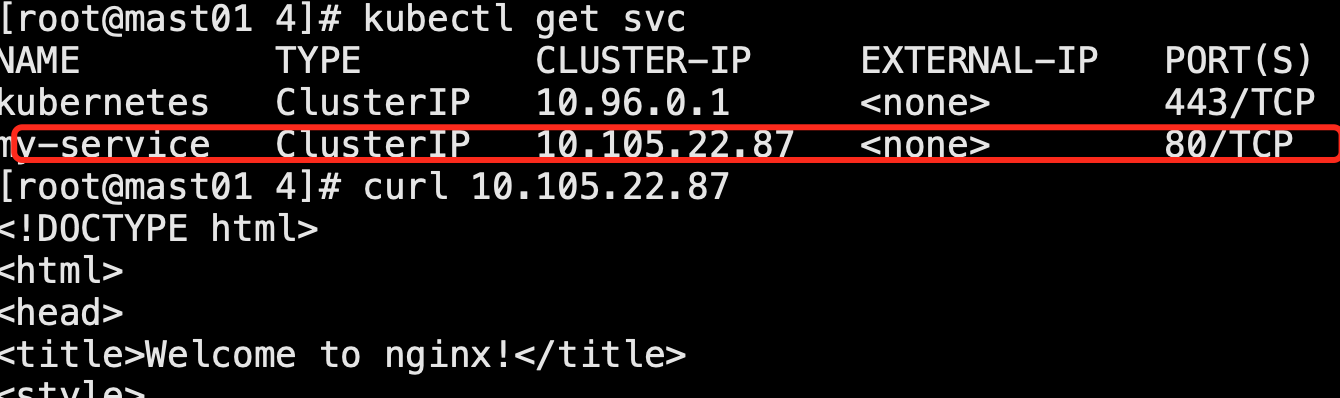
K8S学习之基础十九:k8s的四层代理Service
K8S四层代理Service 四层负载均衡Service 在k8s中,访问pod可以通过ip端口的方式,但是pod是由生命 周期的,pod在重启的时候ip地址往往会发生变化,访问pod就需要新的ip地址,这样就会很麻烦,每次pod地址改变就…...

揭开AI-OPS 的神秘面纱 第六讲 AI 模型服务层 - 开源模型选型与应用 (时间序列场景|图神经网络场景)
时间序列场景 AI 模型服务层 - 开源模型选型与应用 (时间序列场景) 在 AI-Ops 中,时间序列数据分析主要应用于以下场景: 指标预测: 预测 Metrics 指标 (例如 CPU 使用率、内存使用率、网络流量、请求延迟等) 的未来趋势,用于容量规划、资源调度、异常检测等。异常检测: 检…...

在Dify中访问Gemini等模型代理设置指南
问题背景 Google Gemini模型可纯免费使用,且性能也相当不错,一般个人使用或研究足够。但在在国内访问,需设置代理。在Docker部署Dify时,虽然按官方文档介绍设置代理环境变量,但实测发现并不生效。我们通过研究试验解决…...
MySQL的安装以及数据库的基本配置
MySQL的安装及配置 MySQL的下载 选择想要安装的版本,点击Download下载 Mysql官网下载地址: https://downloads.mysql.com/archives/installer/ MySQL的安装 选择是自定义安装,所以直接选择“Custom”,点击“Next” …...

设备树的组成
根节点下含有 compatile 属性的子节点 含有特定 compatile 属性的节点的子节点 如果一个节点的 compatile 属性,它的值是这 4 者之一:"simple-bus","simple-mfd","isa","arm,amba-bus", 那 么 它 的 子结点 (…...

C++入门——输入输出、缺省参数
C入门——输入输出、缺省参数 一、C标准库——命名空间 std C标准库std是一个命名空间,全称为"standard",其中包括标准模板库(STL),输入输出系统,文件系统库,智能指针与内存管理&am…...
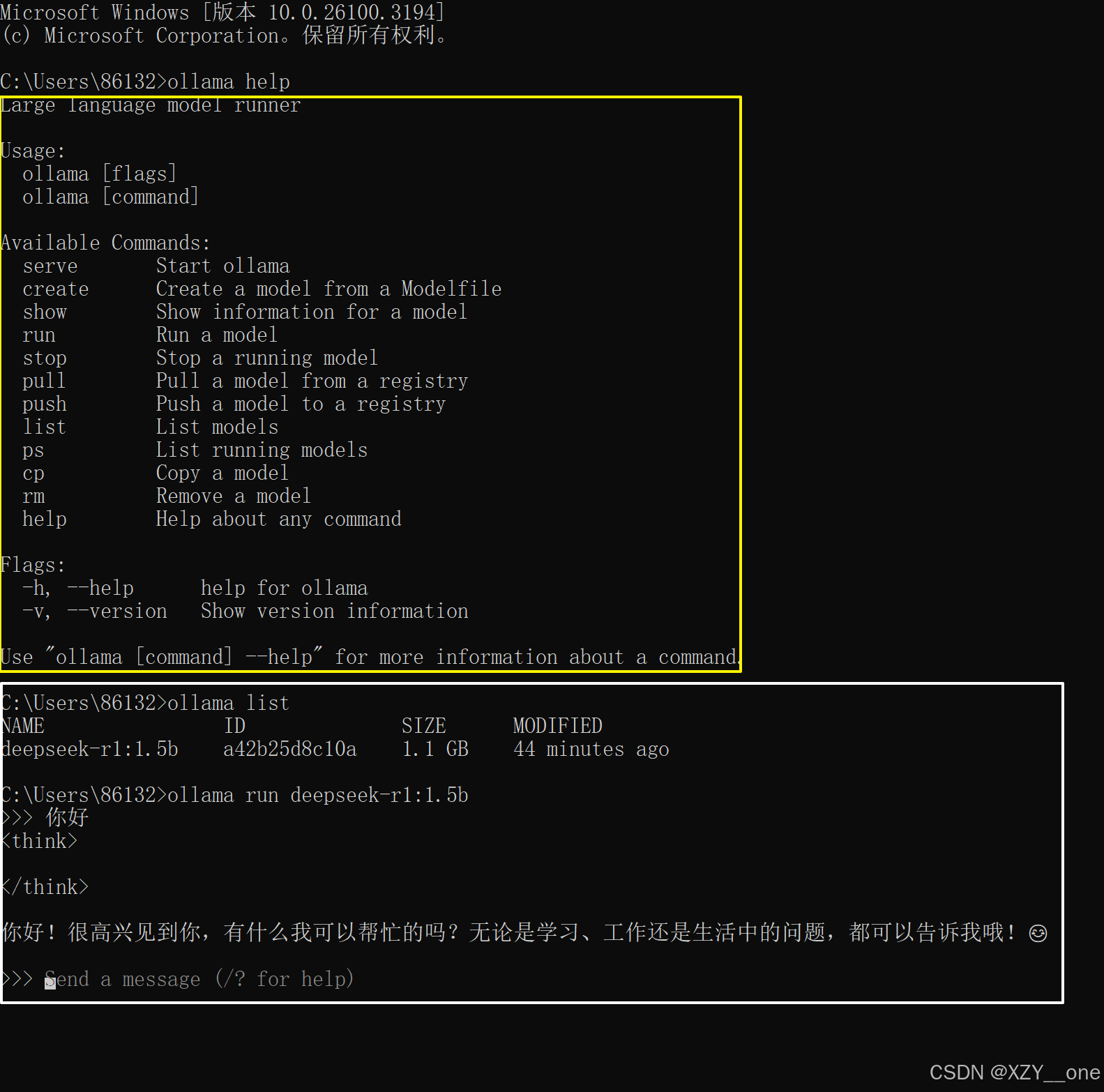
deepseek 本地部署
deepseek 本地部署 纯新手教学,手把手5分钟带你在本地部署一个私有的deepseek,再也不用受网络影响。流畅使用deepseek!!! 如果不想看文章,指路:Deep seek R1本地部署 小白超详细教程 ࿰…...
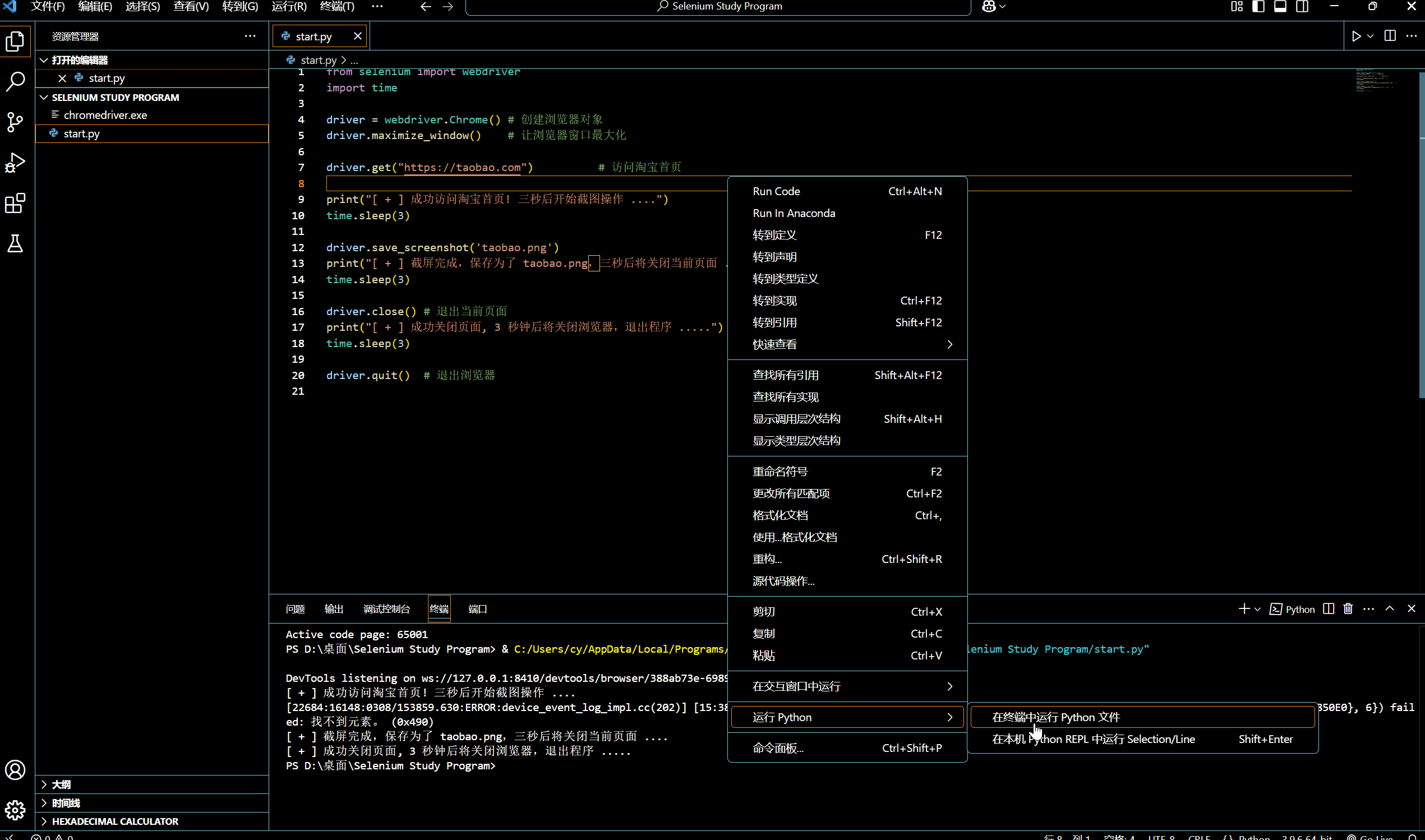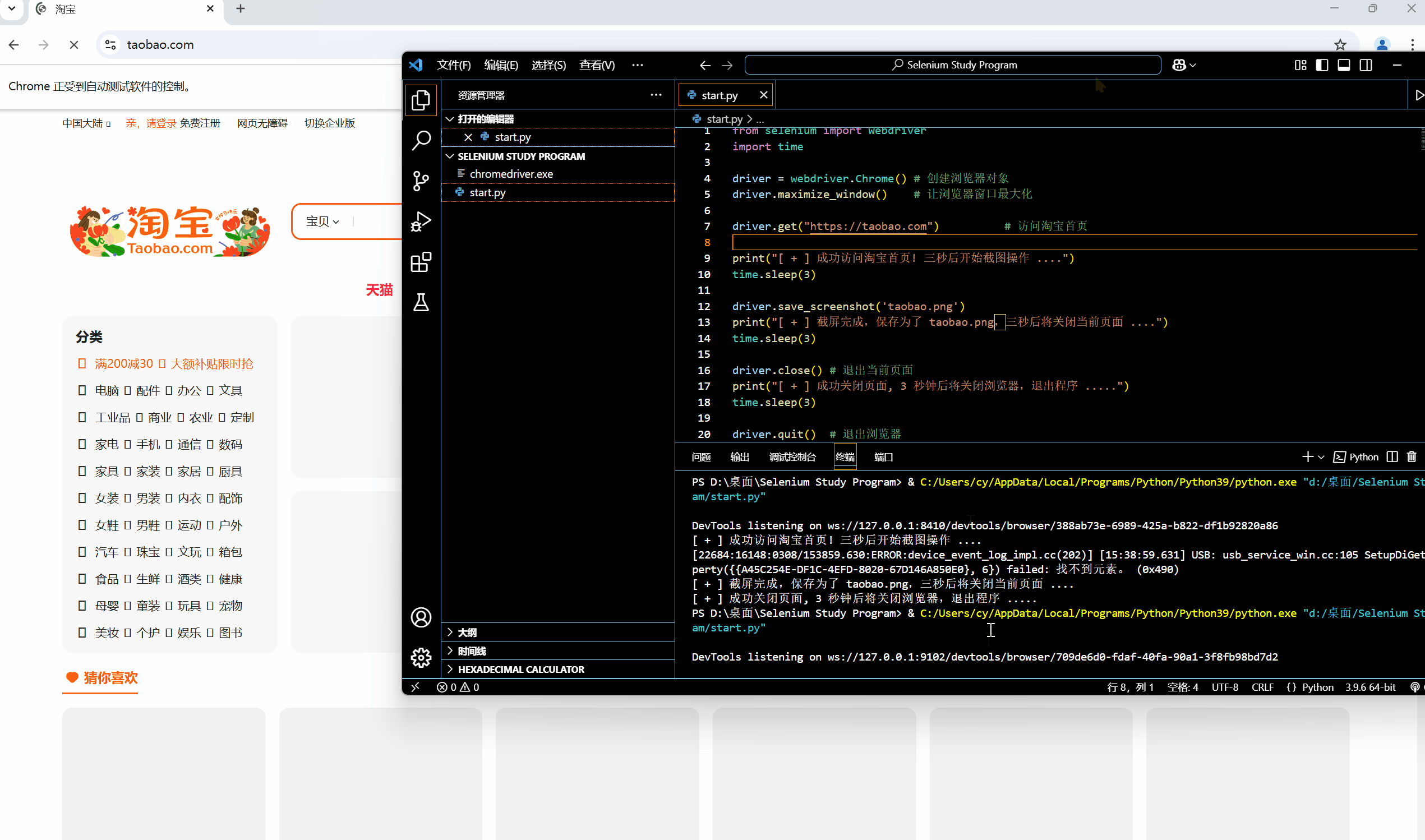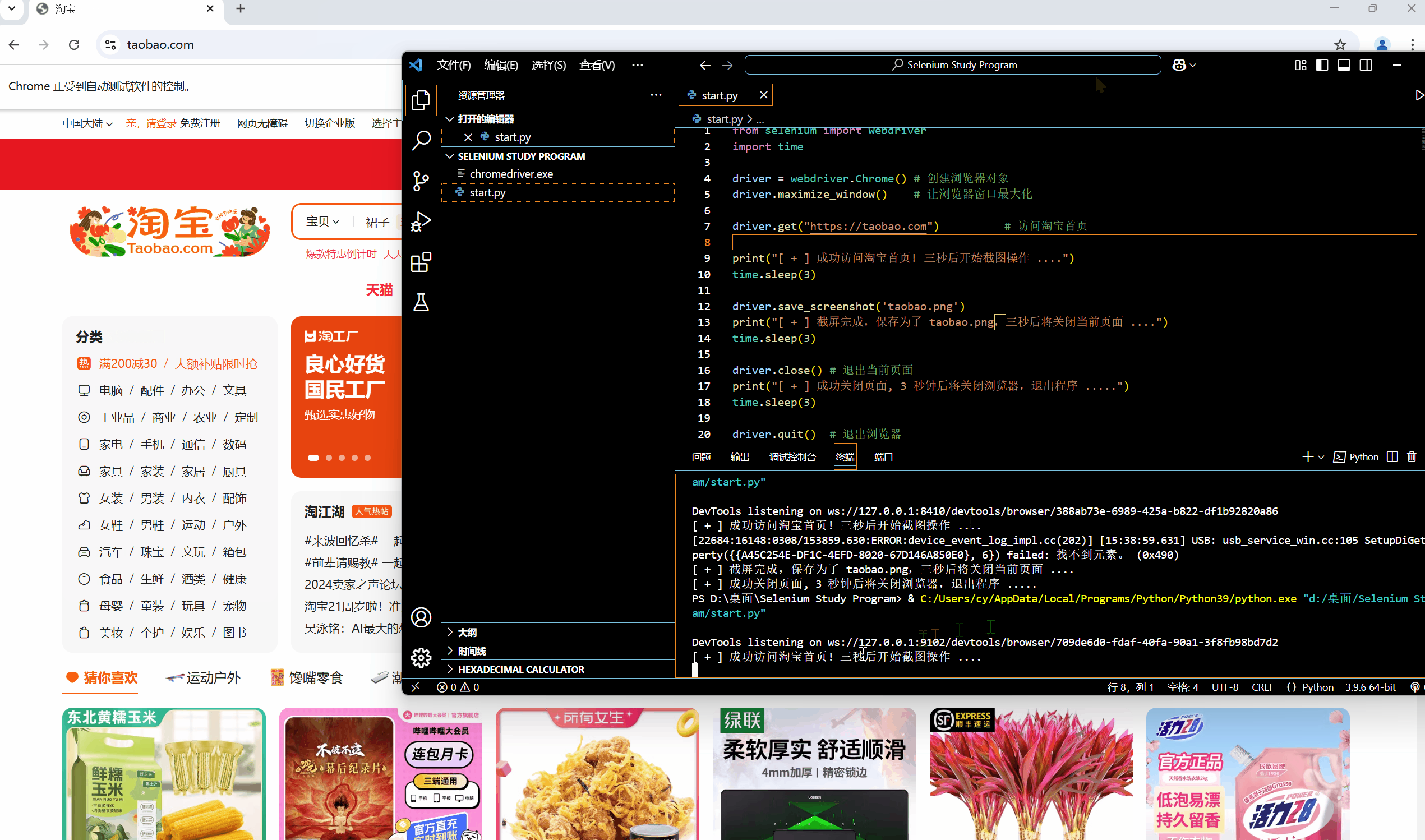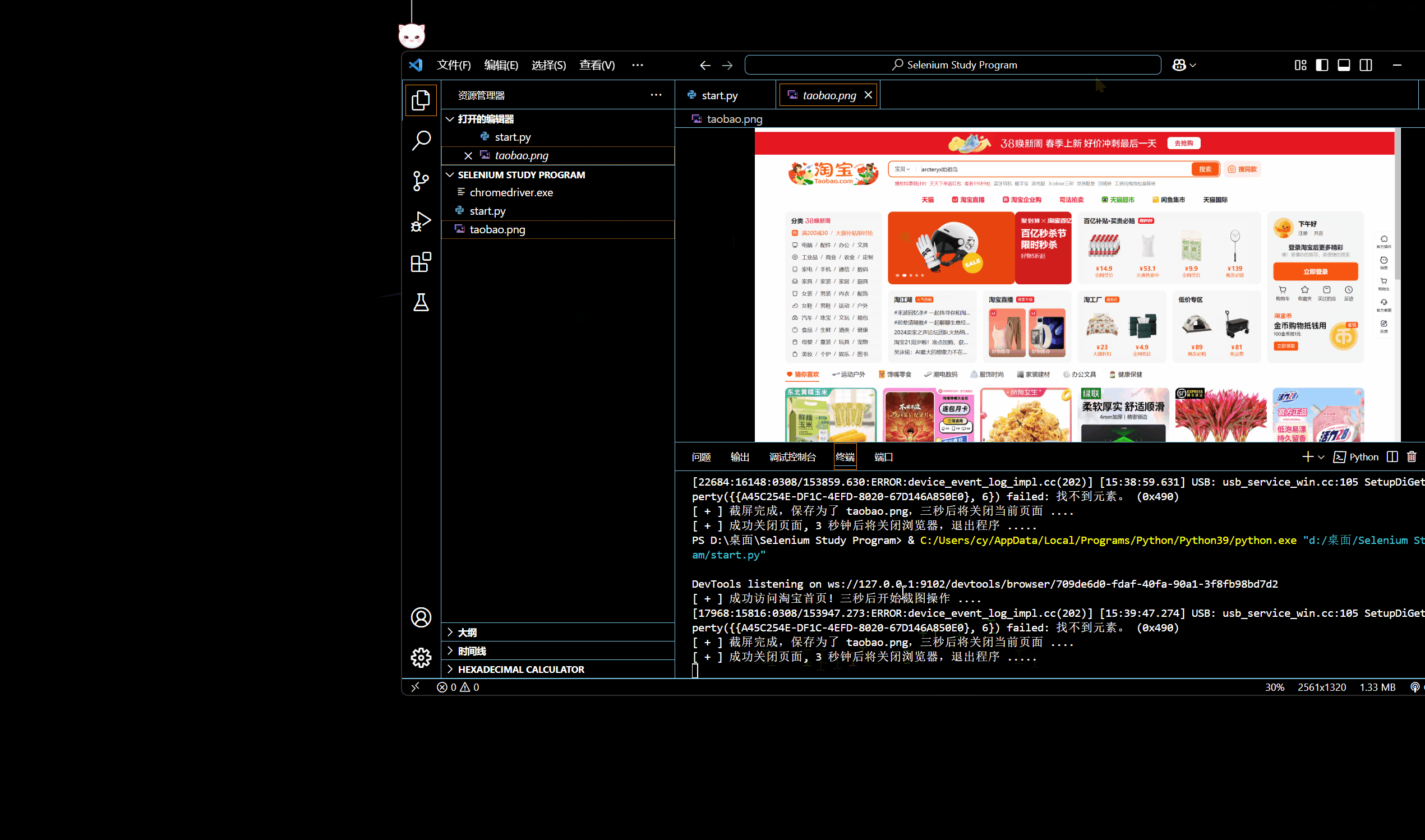
[网络爬虫] 动态网页抓取 — Selenium 入门操作
🌟想系统化学习爬虫技术?看看这个:[数据抓取] Python 网络爬虫 - 学习手册-CSDN博客 0x01:WebDriver 类基础属性 & 方法 为模仿用户真实操作浏览器的基本过程,Selenium 的 WebDriver 模块提供了一个 WebDriver 类…...
)
HTML 超链接(简单易懂较详细)
在 HTML 中,超链接是通过 <a> 标签(anchor tag)创建的。超链接允许用户通过点击文本、图像或其他元素跳转到另一个网页、文件或页面的特定部分。本文将详细介绍 HTML 超链接的语法、属性和应用场景。 一、基本语法 <a href"U…...

rpc和proto
rpc全称远程过程控制,说白了是一种对信息发送和接收的规则编写方法,来自google,这些规则会以protobuf代码存到proto文件里。我以autoGen中agent_worker.proto为例,大概长这样 syntax "proto3";package agents;option …...

OPENGLPG第九版学习 -颜色、像素和片元 PART1
文章目录 4.1 基本颜色理论4.2 缓存及其用途颜色缓存深度缓存 / z缓存 / z-buffer模板缓存 4.2.1 缓存的清除4.2.2 缓存的掩码 4.3 颜色与OpenGL4.3.1 颜色的表达与OpenGL4.3.2 平滑数据插值 4.4 片元的测试与操作4.4.1 剪切测试4.4.2 多重采样的片元操作4.4.3 模板测试模板查询…...

【js逆向】某精灵网
地址:aHR0cHM6Ly93d3cuamluZ2xpbmdzaHVqdS5jb20vYXJ0aWNsZXM f12查看数据包,下面这个不是,你得到的是你的用户信息,需要点击第2页才会显示数据接口 查看载荷 查看预览数据,发现是加密的 查看启动器,看到 Pr…...
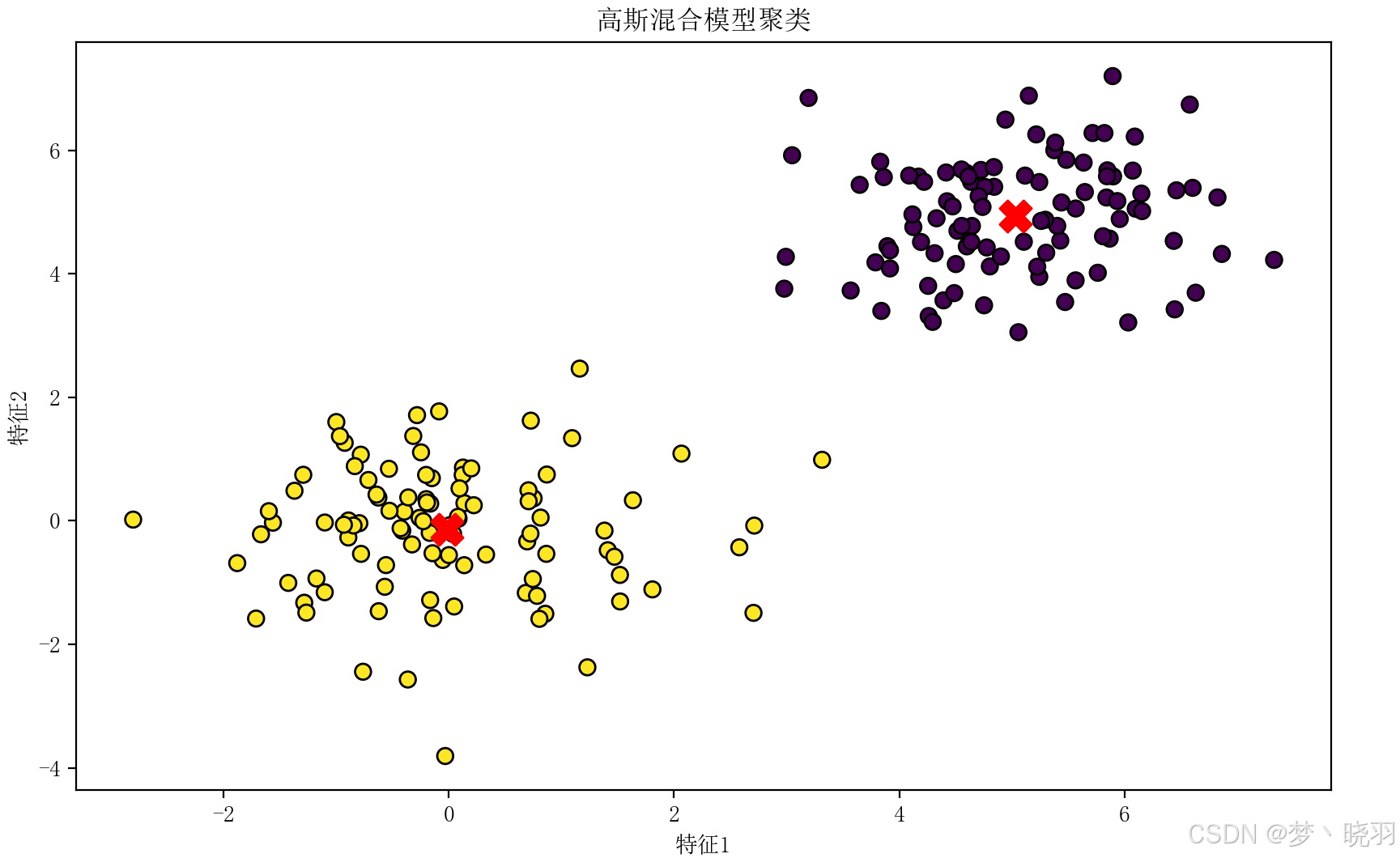
自然语言处理:高斯混合模型
介绍 大家好,博主又来给大家分享知识了,今天给大家分享的内容是自然语言处理中的高斯混合模型。 在自然语言处理这个充满挑战与机遇的领域,我们常常面临海量且复杂的文本数据。如何从这些数据中挖掘出有价值的信息,对文本进行有…...
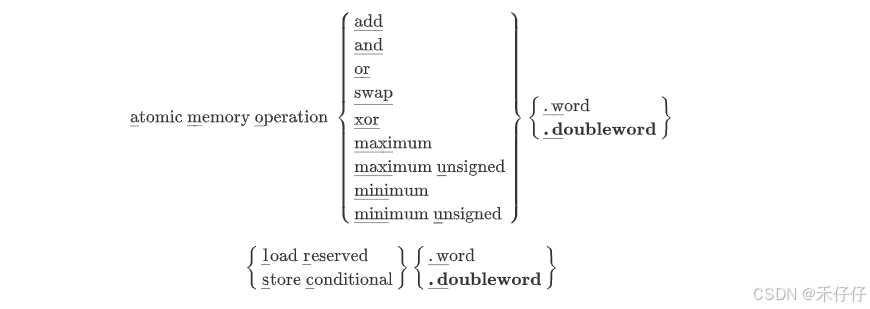
RISC-V汇编学习(三)—— RV指令集
有了前两节对于RISC-V汇编、寄存器、汇编语法等的认识,本节开始介绍RISC-V指令集和伪指令。 前面说了RISC-V的模块化特点,是以RV32I为作为ISA的核心模块,其他都是要基于此为基础,可以这样认为:RISC-V ISA 基本整数指…...
OpenCV连续数字识别—可运行验证
前言 文章开始,瞎说一点其他的东西,真的是很离谱,找了至少两三个小时,就一个简单的需求: 1、利用OpenCV 在Windows进行抓图 2、利用OpenCV 进行连续数字的检测。 3、使用C,Qt 3、将检测的结果显示出来 …...

Python中与字符串操作相关的30个常用函数及其示例
以下是Python中与字符串操作相关的30个常用函数及其示例: 1. str.capitalize() 将字符串的第一个字符大写,其余字符小写。 s "hello world" print(s.capitalize()) # 输出: Hello world2. str.lower() 将字符串中的所有字符转换为小写。…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

MySQL 主从同步异常处理
阅读原文:https://www.xiaozaoshu.top/articles/mysql-m-s-update-pk MySQL 做双主,遇到的这个错误: Could not execute Update_rows event on table ... Error_code: 1032是 MySQL 主从复制时的经典错误之一,通常表示ÿ…...

对象回调初步研究
_OBJECT_TYPE结构分析 在介绍什么是对象回调前,首先要熟悉下结构 以我们上篇线程回调介绍过的导出的PsProcessType 结构为例,用_OBJECT_TYPE这个结构来解析它,0x80处就是今天要介绍的回调链表,但是先不着急,先把目光…...
