2.数据结构-栈和队列
数据结构-栈和队列
- 2.1栈
- 2.1.1栈的表示和实现
- 2.1.2栈的应用举例
- 数制转换
- 括号匹配检验
- 迷宫给求解
- 表达式求值
- 2.1.3链栈的表示和实现
- 2.1.4栈与递归的实现
- 遍历输出链表中各个结点的递归算法
- *Hanoi塔问题的递归算法
- 2.2队列
- 2.2.1循环队列——队列的顺序表示和实现
- 2.2.2链队——队列的链式表示和实现
2.1栈
栈是限定仅在表尾进行插入或删除操作的线性表,因此,对栈来说,表尾端有其特殊含义,称为栈顶(top),相应地,表头称为栈底。

E为栈底元素,A为栈顶元素。也就意味着,栈的修改是按后进先出的原则进行的。因此栈又称为后进先出线性表(简称LIFO结构)。
2.1.1栈的表示和实现
和线性表类似,栈也有两种存储表示方式。
顺序栈,即栈的顺序存储结构是利用一组地址连续的存储单元依次存放自栈底到栈顶的数据元素,同时附设指针top指示栈顶元素在顺序栈中的位置。通常的习惯做法是top=0表示空栈,鉴于C语言中数组的下标约定从0开始,则当以C作描述语言时,如设定会带来很大不便;另一方面,由于栈在使用过程中所需最大空间的大小很难估计,一般来说,在初始化设空栈时不应限定栈的最大容量。一个较合理的做法是;先分配一个基本容量,然后在应用过程中,当栈的空间不够使用时再逐段扩大。为此可设定两个常量:STACK_INIT_SIZE(存储空间初始分配量)和STACKINCREMENT(存储空间分配增量)。
top 并不是栈顶元素,而是指向栈顶元素的下一个位置。
top - 1 才是真正的栈顶元素位置。
typedef struct{SElemType *base; //栈底指针SElemType *top; //栈顶指针,其初值指向栈底int stacksize; //栈当前可使用的最大容量//每当插入心得栈顶元素时,指针top+1
};
顺序栈所有操作汇总:
#include<stdio.h>
#include<stdlib.h>#define SElemType int
#define STACK_INIT_SIZE 100 //存储空间初始分配量
#define STACKINCREMENT 10 //存储空间分配增量
#define Status inttypedef struct{SElemType *base;SElemType *top;int stacksize;
} SqStack; Status InitStack (SqStack &S){//构造一个空栈S.base = (SElemType *) malloc(STACK_INIT_SIZE * sizeof(SElemType));if(!S.base) exit(0); //存储分配失败S.top = S.base;S.stacksize = STACK_INIT_SIZE;return 1;
}Status Push(SqStack &S, SElemType e){//插入元素e为新的栈顶元素if(S.top - S.base >= S.stacksize){ //栈满.追加存储空间 S.base = (SElemType *) realloc(S.base, (S.stacksize + STACKINCREMENT) * sizeof(SElemType));if(!S.base) exit(0); //存储分配失败S.top = S.base + S.stacksize;S.stacksize += STACKINCREMENT; } *S.top++ = e;return 1;
}Status Pop(SqStack &S, SElemType &e){//若栈不为空,则删除S的栈顶元素,用e返回其值if(S.top == S.base) return 0; //空栈e = * --S.top; //先将S.top赋值给e,再自减return 1;
}Status GetTop(SqStack &S, SElemType &e){//若栈不为空,则用e返回S的栈顶元素if(S.top == S.base) return 0;e = *(S.top - 1);return 1;
}int StackLength(SqStack &S){//返回栈的元素个数,即栈的长度 return S.top - S.base;
}int StackEmpty(SqStack &S){//返回栈是否为空,为空返回0,不为空返回1if(!StackLength(S)) return 0;return 1;
}void ClearStack(SqStack &S){//把S置为空栈S.top = S.base;
}void DestroyStack(SqStack &S){//销毁栈 if(S.base){free(S.base);S.base = S.top = NULL;S.stacksize = 0;}
}int main()
{SqStack S;InitStack(S);Push(S, 1);Push(S, 2);int e; Pop(S, e);printf("%d\n", e);GetTop(S, e);printf("%d\n", e);int l = StackLength(S);printf("length: %d\n", l);return 0;
}
2.1.2栈的应用举例
数制转换
将十进制数N和其他d进制数的转换。算法原理如下:
N = ( N / d ) ∗ d + N m o d d N = (N/d)*d+N \ \ mod \ \ d N=(N/d)∗d+N mod d
要求: 对于输入的任意一个非负十进制整数,打印与其等值的八进制数。
//栈的操作与2.1.1中代码相同
int main()
{SqStack S;InitStack(S);printf("请输入一个非负的十进制数: ");int numT;scanf("%d", &numT);while(numT){Push(S, numT % 8);numT /= 8;} int e;while(StackEmpty(S)){Pop(S, e);printf("%d", e);}return 0;
}
括号匹配检验
假设表达式中允许包含两种括号:圆括号和方括号,其嵌套顺序随意,即()为正确格式,[{]为不正确格式。
要求: 输入只含圆括号和方括号的字符串,判断其是否是正确的格式。
//要加上#include<string.h>
int main()
{SqStack S;InitStack(S);char str[100];printf("输入只含圆括号和方括号的字符串: ");scanf("%s", str);int length = strlen(str), i, flag = 1, e;//(为1, )为2, [为3, ]为4 for(i = 0; i < length; i ++){if(str[i] == '[') Push(S, 3);if(str[i] == '(') Push(S, 1);if(str[i] == ')') {GetTop(S, e);if(e == 1) Pop(S, e);} if(str[i] == ']') {GetTop(S, e);if(e == 3) Pop(S, e);}}if(!StackEmpty(S)) printf("%s是合法字符串\n", str);else printf("%s不是合法字符串\n", str);return 0;
}
迷宫给求解
链接: C语言 严蔚敏 数据结构 迷宫求解_顺序栈应用
类似于深度优先搜索,用栈去模拟这个过程。
表达式求值
链接: C语言 严蔚敏 数据结构 表达式求值_顺序栈应用
类似于括号匹配检验。
2.1.3链栈的表示和实现
链栈是指采用链式存储结构实现的栈。通常链栈用单链表来实现。

由于栈的主要操作是在栈顶插入和删除,显然以链表的头部作为栈顶是最方便的。
#include<stdio.h>
#include<stdlib.h>#define List_Init_Size 100 //线性表存储空间的初始分配量
#define ListIncreMent 10 //线性表存储空间的分配增量
#define ElemType int
#define Status inttypedef struct StackNode{ElemType data;struct StackNode *next;
}StackNode, *LinkStack;Status InitStack(LinkStack &S) {// 构造一个空栈,栈顶指针为空S = NULL;return 1;
}Status Push(LinkStack &S, ElemType e) {//和顺序栈的入栈不同,链栈的入栈前不需要判断栈是否满,只需要为入栈动态分配一个节点空间StackNode *p = (StackNode *)malloc(sizeof(StackNode)); // 使用 malloc 分配内存if (p == NULL) {// 内存分配失败的处理return 0;}p->data = e;p->next = S;S = p; // 栈顶指针指向新节点return 1;
}Status Pop(LinkStack &S, ElemType &e) {if (S == NULL) {return 0; // 空栈,返回失败}e = S->data; // 获取栈顶元素StackNode *p = S; // 声明指针 p,指向栈顶元素S = S->next; // 将栈顶指针指向下一个元素free(p); // 释放栈顶元素的内存return 1; // 返回成功
}ElemType GetTop(LinkStack S){//返回S的栈顶元素 if(S != NULL) return S->data;
}int main()
{LinkStack S;InitStack(S);int i, e;for(i = 1; i <= 10; i ++){Push(S, i);}Pop(S, e);printf("%d\n", e);
}
2.1.4栈与递归的实现
对于链表,其结点LNode的定义由数据域data和指针域next组成,而指针域next是一种指向LNode类型的指针,即LNode的定义中又用到了其自身所以链表是一种递归的数据结构。
遍历输出链表中各个结点的递归算法
算法从前向后遍历输出链表结点的递归算法,直到p为NULL时递归结束,在递归过程中,p不断指向后续节点。
#include<stdio.h>
#include<stdlib.h>#define List_Init_Size 100 //线性表存储空间的初始分配量
#define ListIncreMent 10 //线性表存储空间的分配增量
#define ElemType int
#define Status inttypedef struct LNode{ElemType data;struct LNode *next;
}LNode, *LinkList;void CreateList_L(LinkList &L, int n)
{// 尾插法L = (LinkList) malloc(sizeof (LNode));L->next = NULL; LinkList tail = L; // tail指向链表的尾部printf("请输入\n"); //先建立一个带头结点的单链表for (int i = n; i > 0; --i){LinkList p = (LinkList) malloc(sizeof (LNode)); //生成新结点scanf("%d", &p->data);p->next = NULL;tail->next = p;tail = p;}
}
void TraverseList(LinkList p){if(p == NULL) return;else{printf("%d\n", p->data);TraverseList(p->next);}
}
int main()
{LinkList L;int i, e;CreateList_L(L, 10);TraverseList(L->next);return 0;
}
*Hanoi塔问题的递归算法
#include<stdio.h>
#include<stdlib.h>int m = 0;void move(char A, int n, char C){ //将编号为n的圆盘从A移到C printf("%d, %d, %c, %c\n", ++m, n, A, C);
}void Hanoi(int n, char A, char B, char C){if(n == 1) move(A, 1, C); //将编号为1的圆盘从A移到Celse{Hanoi(n-1, A, C, B); //将A上编号1~n-1的圆盘移到B, C做辅助塔move(A, n, C); //将编号为n的圆盘从A到CHanoi(n-1, B, A, C); //将B上编号为1~n-1的圆盘移到C, A做辅助塔 }
}int main()
{int n = 3;Hanoi(n, 'A', 'B', 'C');return 0;
}
递归算法的时间复杂度为 O ( 2 n ) O(2^n) O(2n),空间复杂度则为 O ( n ) O(n) O(n)
2.2队列
队列的操作与栈的操作类似,不同的是,删除实在表的头部(即队头)进行。
队列(Queue)是一种 先进先出(FIFO,First-In-First-Out)的线性数据结构,它的基本特点是元素的插入发生在队尾,而元素的删除发生在队头。队列通常用来处理需要按照顺序处理的数据,类似于排队的过程。
2.2.1循环队列——队列的顺序表示和实现
队列也有两种表示,顺序表示和链式表示。
在队列的顺序存储结构中,除了用一组连续的存储单元依次存放从队列头到队列尾的元素外,尚需要附设两个整型变量front和rear分别指示队列头元素和队列尾元素的位置。在初始化创建空队列时,令front = rear = 0,每当插入新的队列尾元素,尾指针+1,每当删除队列头元素
时,头指针front+1。在非空队列中头指针始终指向队列头元素,而尾指针始终指向队列尾元素的下一个位置。
为了避免队列实际空间并未占满而出现“假溢出现象”,我们将顺序队列变为一个环状的空间,称为循环队列。头尾指针以及队列元素之间关系不变,只是在循环队列中,头尾指针“依环状态增1”的操作可用“模”运算来实现。通过取模,头指针和尾指针就可以在顺序表空间内以头尾衔接的方式“循环移到”。
假溢出现象解释:就是因为删除操作会让头指针+1,导致头指针之前的空间就不会被利用起来,而当尾指针的值到达队列的空间最大值时,就会产生假溢出了。
如何判断队列是否为空或者队列是否已满
少用一个元素空间,即队列空间大小为m时,有m-1个元素就认为是队满。即当头尾指针的值相同时,则认为队空;而当尾指针在循环意义上+1后是等于头指针则认为队满。
队空的条件: Q . f r o n t = Q . r e a r Q.front = Q.rear Q.front=Q.rear
队满的条件:$ Q.front = (Q.rear+1)%MAXQSIZE $
#include<iostream>#define MAXQSIZE 100
#define QElemType int
#define Status intusing namespace std;typedef struct{QElemType *base; // 存储空间的基地址int front; // 队头指针int rear; // 队尾指针
} SqQueue;Status InitQueue(SqQueue &Q) {// 构造一个空队列QQ.base = new QElemType[MAXQSIZE];if(!Q.base) exit(0);Q.front = Q.rear = 0;return 1; // 返回成功
}int QueueLength(SqQueue Q){//返回Q的元素个数return (Q.rear - Q.front + MAXQSIZE) % MAXQSIZE;
}Status EnQueue(SqQueue &Q, QElemType e){//插入元素e为Q的新的队尾元素if((Q.rear + 1) % MAXQSIZE == Q.front){ //队满return 0;}Q.base[Q.rear] = e;Q.rear = (Q.rear + 1) % MAXQSIZE;return 1;
}Status DeQueue(SqQueue &Q, QElemType &e){//删除Q的队头元素,用e返回其值if(Q.front == Q.rear) return 0; //队空e = Q.base[Q.front];Q.front = (Q.front + 1) %MAXQSIZE;return 1;
}QElemType GetHead(SqQueue Q){//返回Q的队头元素,不修改队头指针if(Q.front != Q.rear) return Q.base[Q.front];
}int main()
{SqQueue Q;InitQueue(Q);for(int i = 1; i <= 10; i ++){EnQueue(Q, i);}int e = GetHead(Q);cout << e << endl;return 0;}
2.2.2链队——队列的链式表示和实现

一个链队需要两个分别指示队头和队尾的指针才能唯一确定,给链队添加一个头结点,并令指针始终指向头结点。
链队的操作即为单链表插入和删除操作的特殊情况,只是需进一步修改尾指针或头指针。

这个图对于理解链队很重要
#include<iostream>#define MAXQSIZE 100
#define QElemType int
#define Status intusing namespace std;typedef struct QNode{QElemType data;struct QNode *next;
} QNode, *QueuePtr; //链队的每个结点typedef struct{QueuePtr front;QueuePtr rear;
}LinkQueue; //这就是链队的头指针Status InitQueue(LinkQueue &Q){//构造一个空队列QQ.front = Q.rear = new QNode;Q.front->next = NULL;return 1;
}Status EnQueue(LinkQueue &Q, QElemType e){//插入元素e为Q的队尾元素QueuePtr p = new QNode; //新节点分配内存 **p->data = e;p->next = NULL;Q.rear->next = p;Q.rear = p; //类似尾插法return 1;
}Status DeQUeue(LinkQueue &Q, QElemType &e){//删除Q的队头元素if(Q.front == Q.rear) return 0; //空队QueuePtr p = Q.front;e = p->data;Q.front->next = p->next; //修改头指针if(Q.rear == p) Q.rear = Q.front; //删除的最后一个元素delete p;return 1;
}QElemType GetHead(LinkQueue Q){//返回Q的队头元素,不修改队头指针if(Q.front != Q.rear)return Q.front->next->data;
}int main()
{LinkQueue Q;InitQueue(Q);for(int i = 1; i <= 10; i ++){EnQueue(Q, i);}cout << GetHead(Q) << endl;return 0;}

相关文章:

2.数据结构-栈和队列
数据结构-栈和队列 2.1栈2.1.1栈的表示和实现2.1.2栈的应用举例数制转换括号匹配检验迷宫给求解表达式求值 2.1.3链栈的表示和实现2.1.4栈与递归的实现遍历输出链表中各个结点的递归算法*Hanoi塔问题的递归算法 2.2队列2.2.1循环队列——队列的顺序表示和实现2.2.2链队——队列…...

aws(学习笔记第三十一课) aws cdk深入学习(batch-arm64-instance-type)
aws(学习笔记第三十一课) aws cdk深入学习 学习内容: 深入练习aws cdk下部署batch-arm64-instance-type 1. 深入练习aws cdk下部署batch-arm64-instance-type 代码链接 代码链接 代码链接 -> batch-arm64-instance-type之前代码学习 之前学习代码链接 -> aw…...

MySQL 中,SELECT ... FOR UPDATE
在 MySQL 中,SELECT ... FOR UPDATE 语句会对查询结果集中的行加排他锁(X 锁)。关于其他事务是否能读取当前行,以下是详细说明: 1. 排他锁(X 锁)的特性 排他锁是一种独占锁,加锁后&…...

云服务运维智能时代:阿里云操作系统控制台
阿里云操作系统控制台 引言需求介绍操作系统使用实例获得的帮助与提升建议 引言 阿里云操作系统控制台是一款创新型云服务器运维工具,专为简化用户的运维工作而设计。它采用智能化和可视化的方式,让运维变得更加高效、直观。借助AI技术,控制…...

【Agent的革命之路——LangGraph】如何使用config
有时我们希望在调用代理时能够对其进行配置。这包括配置使用哪个语言模型(LLM)等例子。下面我们将通过一个示例来详细介绍如何进行这样的配置。 在介绍 configurable 之前我们先介绍一下 Langchain 的 RunnableConfig。RunnableConfig是一个配置对象&…...

ArcGIS操作:15 计算点的经纬度,并添加到属性表
注意:需要转化为地理坐标系 1、打开属性表,添加字段 2、计算字段(以计算纬度为例 !Shape!.centroid.Y ) 3、效果...

Docker基础入门
第 1 章:核心概念与安装配置 本章首先介绍Docker 的三大核心概念: 镜像 (Image)容器(Container)仓库(Repository) 只有理解了这三个核心概念,才能顺利地理解Docker容器的整个生命周期。 随后࿰…...

【Linux】详谈 基础I/O
目录 一、理解文件 狭义的理解: 广义理解: 文件操作的归类认知 系统角度 二、系统文件I/O 2.1 标志位的传递 系统级接口open 编辑 open返回值 写入文件 读文件 三、文件描述符 3.1(0 & 1 & 2) 3.2 文件描…...

爬虫案例七Python协程爬取视频
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、Python协程爬取视频 前言 提示:这里可以添加本文要记录的大概内容: 爬虫案例七协程爬取视频 提示:以下是本篇文章正文…...

[20250304] 关于 RISC-V芯片 的介绍
[20250304] 关于 RISC-V芯片 的介绍 1. 调研报告 一、RISC-V 芯片结构分析 RISC-V 芯片基于开源指令集架构(ISA),其核心优势在于模块化设计与高度灵活性。 指令集架构 基础指令集:包含 RV32I(32 位)、R…...
一学就会:A*算法详细介绍(Python)
📢本篇文章是博主人工智能学习以及算法研究时,用于个人学习、研究或者欣赏使用,并基于博主对相关等领域的一些理解而记录的学习摘录和笔记,若有不当和侵权之处,指出后将会立即改正,还望谅解。文章分类在&am…...
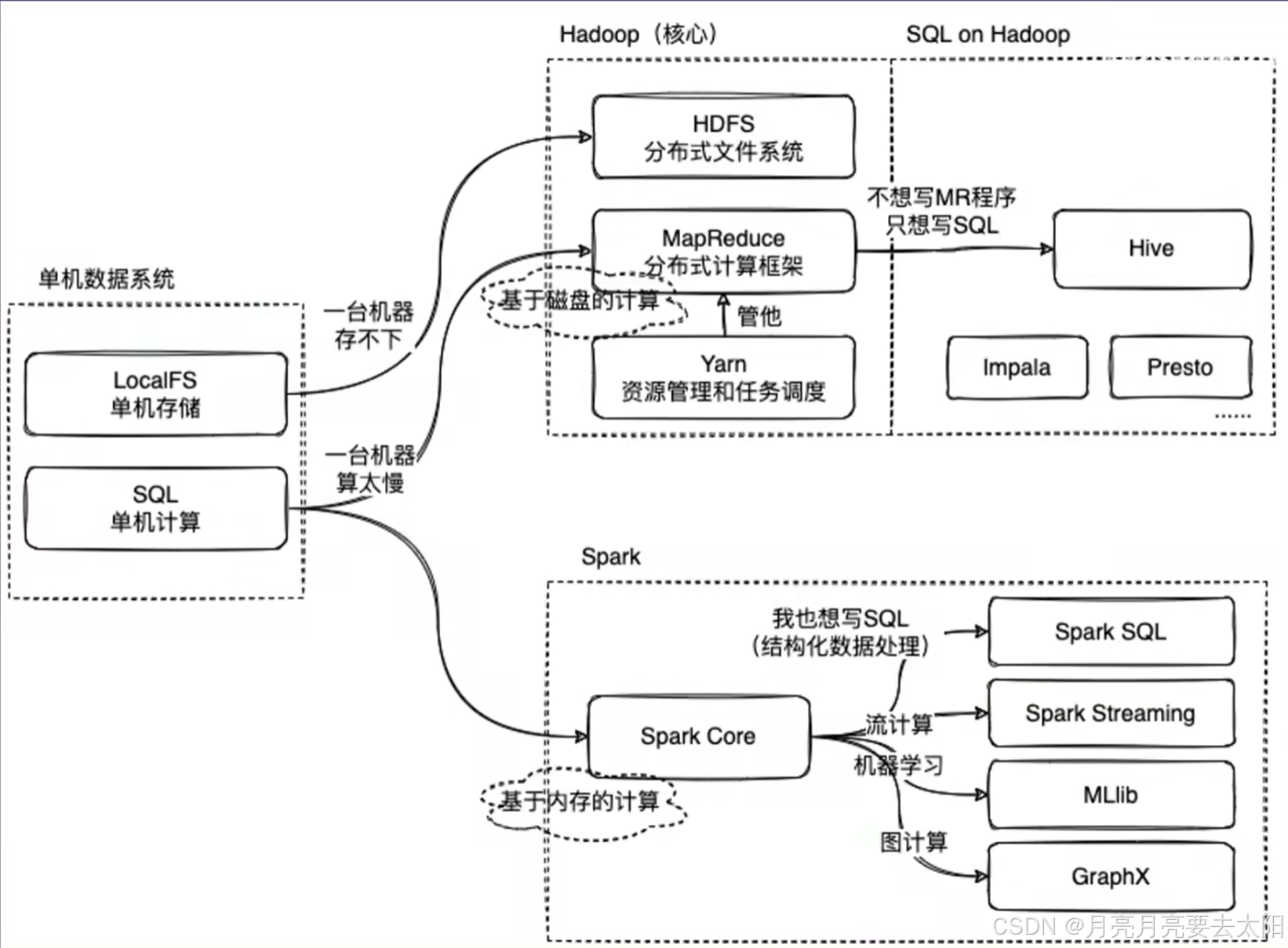
Hadoop、Hive、Spark的关系
Part1:Hadoop、Hive、Spark关系概览 1、MapReduce on Hadoop 和spark都是数据计算框架,一般认为spark的速度比MR快2-3倍。 2、mapreduce是数据计算的过程,map将一个任务分成多个小任务,reduce的部分将结果汇总之后返回。 3、HIv…...

Excel·VBA江西省预算一体化工资表一键处理
每月制作工资表导出为Excel后都需要调整格式,删除0数据的列、对工资表项目进行排序、打印设置等等,有些单位还分有“行政”、“事业”2个工资表就需要操作2次。显然,这种重复操作的问题,可以使用VBA代码解决 目录 代码使用说明1&a…...
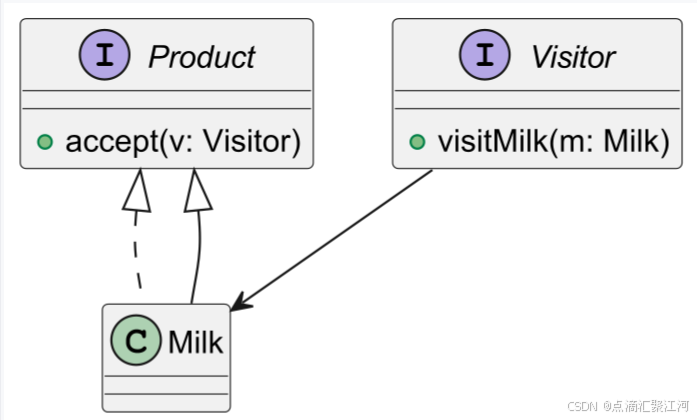
23种设计模式简介
一、创建型(5种) 1.工厂方法 总店定义制作流程,分店各自实现特色披萨(北京店-烤鸭披萨,上海店-蟹粉披萨) 2.抽象工厂 套餐工厂(家庭装含大披萨薯条,情侣装含双拼披萨红酒&#…...

python fire 库与 sys.argv 处理命令行参数
fire库 Python Fire 由Google开发,它使得命令行接口(CLI)的创建变得容易。使用Python Fire,可以将Python对象(如类、函数或字典)转换为可以从终端运行的命令行工具。这能够以一种简单而直观的方式与你的Py…...

PDF处理控件Aspose.PDF,如何实现企业级PDF处理
PDF处理为何成为开发者的“隐形雷区”? “手动调整200页PDF目录耗时3天,扫描件文字识别错误导致数据混乱,跨平台渲染格式崩坏引发客户投诉……” 作为开发者,你是否也在为PDF处理的复杂细节消耗大量精力?Aspose.PDF凭…...
Spring(1)——mvc概念,部分常用注解
1、什么是Spring Web MVC? Spring MVC 是一种基于 Java 的实现了 MVC(Model-View-Controller,模型 - 视图 - 控制器)设计模式的 Web 应用框架,它是 Spring 框架的一个重要组成部分,用于构建 Web 应用程序。…...
C语言(23)
字符串函数 11.strstr函数 1.1函数介绍: 头文件:string.h char *strstr ( const char * str1,const char *str2); 作用:在一个字符串(str1)中寻找另外一个字符串(str2)是否出现过 如果找到…...
Immich自托管服务的本地化部署与随时随地安全便捷在线访问数据
文章目录 前言1.关于Immich2.安装Docker3.本地部署Immich4.Immich体验5.安装cpolar内网穿透6.创建远程链接公网地址7.使用固定公网地址远程访问 前言 小伙伴们,你们好呀!今天要给大家揭秘一个超炫的技能——如何把自家电脑变成私人云相册,并…...
基于SpringBoot的在线付费问答系统设计与实现(源码+SQL脚本+LW+部署讲解等)
专注于大学生项目实战开发,讲解,毕业答疑辅导,欢迎高校老师/同行前辈交流合作✌。 技术范围:SpringBoot、Vue、SSM、HLMT、小程序、Jsp、PHP、Nodejs、Python、爬虫、数据可视化、安卓app、大数据、物联网、机器学习等设计与开发。 主要内容:…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...

淘宝扭蛋机小程序系统开发:打造互动性强的购物平台
淘宝扭蛋机小程序系统的开发,旨在打造一个互动性强的购物平台,让用户在购物的同时,能够享受到更多的乐趣和惊喜。 淘宝扭蛋机小程序系统拥有丰富的互动功能。用户可以通过虚拟摇杆操作扭蛋机,实现旋转、抽拉等动作,增…...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...

mac:大模型系列测试
0 MAC 前几天经过学生优惠以及国补17K入手了mac studio,然后这两天亲自测试其模型行运用能力如何,是否支持微调、推理速度等能力。下面进入正文。 1 mac 与 unsloth 按照下面的进行安装以及测试,是可以跑通文章里面的代码。训练速度也是很快的。 注意…...

从物理机到云原生:全面解析计算虚拟化技术的演进与应用
前言:我的虚拟化技术探索之旅 我最早接触"虚拟机"的概念是从Java开始的——JVM(Java Virtual Machine)让"一次编写,到处运行"成为可能。这个软件层面的虚拟化让我着迷,但直到后来接触VMware和Doc…...
