mIoU Class与mIoU Category的区别
mIoU(mean Intersection over Union)是语义分割任务中常用的评估指标,用于衡量模型预测的分割结果与真实标签之间的重叠程度。mIoU Class 和 mIoU Category 的区别主要体现在计算方式和应用场景上:
1. mIoU Class
- 定义:mIoU Class 是基于每个类别的 IoU 计算平均值。
- 计算方式:
- 对每个类别分别计算 IoU(预测区域与真实标签的交集除以它们的并集)。
- 对所有类别的 IoU 取平均。
- 特点:
- 每个类别的权重相同,无论类别的大小或出现频率如何。
- 适用于类别均衡的数据集,或者需要平等对待每个类别的场景。
- 公式
mIoU Class = 1 N ∑ i = 1 N IoU i \text{mIoU Class} = \frac{1}{N} \sum_{i=1}^{N} \text{IoU}_i mIoU Class=N1i=1∑NIoUi
其中, N N N 是类别总数, IoU i \text{IoU}_i IoUi 是第 i i i 个类别的 IoU。
2. mIoU Category
- 定义:mIoU Category 是基于更高层次的类别分组(Category)计算 IoU 的平均值。
- 计算方式:
- 将多个细粒度类别(Class)合并为更高层次的类别(Category)。
- 对每个 Category 计算 IoU。
- 对所有 Category 的 IoU 取平均。
- 特点:
- 适用于需要评估模型在更高层次语义上的表现。
- 可以减少类别不平衡的影响,因为多个细粒度类别被合并为一个 Category。
- 公式:
mIoU Category = 1 M ∑ j = 1 M IoU j \text{mIoU Category} = \frac{1}{M} \sum_{j=1}^{M} \text{IoU}_j mIoU Category=M1j=1∑MIoUj
其中, M M M 是 Category 的总数, IoU j \text{IoU}_j IoUj 是第 j j j 个 Category 的 IoU。
3. 区别总结
| 特性 | mIoU Class | mIoU Category |
|---|---|---|
| 计算粒度 | 细粒度(每个类别单独计算) | 粗粒度(类别分组后计算) |
| 适用场景 | 类别均衡的数据集 | 类别不平衡或需要高层次语义评估 |
| 权重分配 | 每个类别权重相同 | 每个 Category 权重相同 |
| 计算复杂度 | 较高(类别多时计算量大) | 较低(类别分组后计算量减少) |
4. 举例说明
假设有一个数据集包含以下类别:
-
Class:猫、狗、汽车、卡车
-
Category:动物(猫、狗)、车辆(汽车、卡车)
-
mIoU Class:分别计算猫、狗、汽车、卡车的 IoU,然后取平均。
-
mIoU Category:将猫和狗合并为“动物”,汽车和卡车合并为“车辆”,分别计算动物和车辆的 IoU,然后取平均。
5. 选择依据
- 如果需要评估模型对每个细粒度类别的表现,使用 mIoU Class。
- 如果关注更高层次的语义分割效果,或者类别不平衡,使用 mIoU Category。
希望这个解释能帮助你理解两者的区别!如果还有其他问题,欢迎继续提问。
相关文章:

mIoU Class与mIoU Category的区别
mIoU(mean Intersection over Union)是语义分割任务中常用的评估指标,用于衡量模型预测的分割结果与真实标签之间的重叠程度。mIoU Class 和 mIoU Category 的区别主要体现在计算方式和应用场景上: 1. mIoU Class 定义ÿ…...

深入解析 C 语言中含数组和指针的构造体与共同体内存计算
在 C 语言中,构造体(struct)和共同体(union)允许我们将多种数据类型组合到一起。除了常见的基本数据类型之外,经常还会在它们中嵌入数组和指针。由于数组的内存是连续分配的,而指针的大小与平台…...
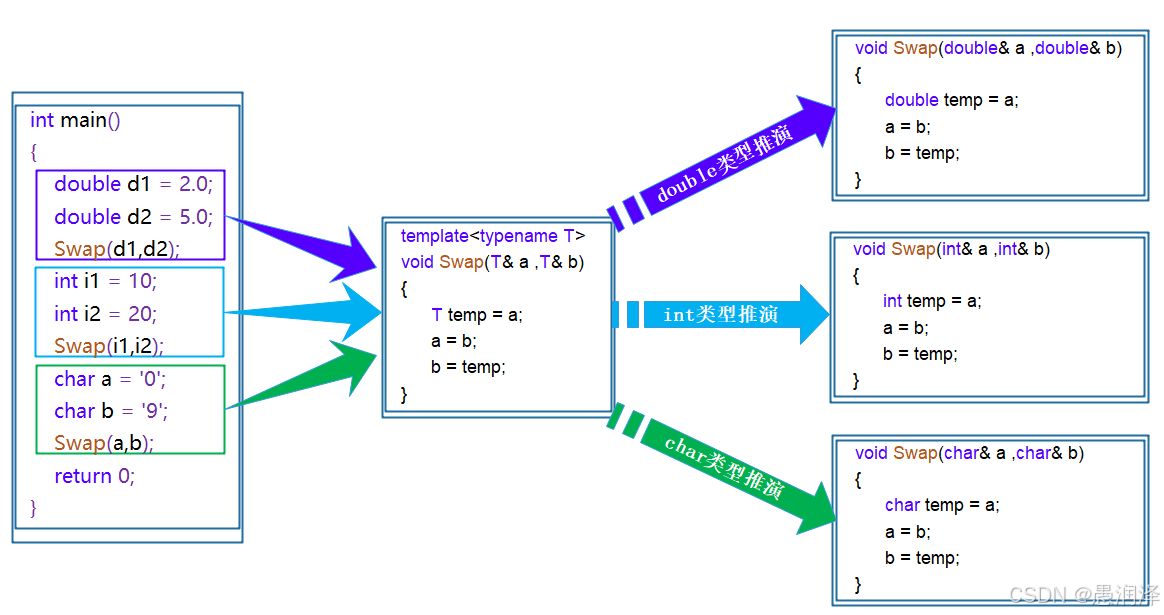
【C++模板】:开启泛型编程之门(函数模版,类模板)
📝前言: 在上一篇文章C内存管理中我们介绍了C的内存管理,重点介绍了与C语言的区别,以及new和delete。这篇文章我们将介绍C的利器——模板。 在C编程世界里,模板是一项强大的特性,它为泛型编程奠定了坚实基础…...

HEC-HMS水文建模全解析:气候变化与极端水文、离散化流域单元精准刻画地表径流、基流与河道演进过程
一、技术革新:数字流域的精密算法革命 在全球气候变化与极端水文事件频发的双重压力下,HEC-HMS模型凭借其半分布式建模架构与多尺度仿真能力,已成为现代流域管理的核心工具。该模型通过离散化流域单元精准刻画地表径流、基流与河…...
具备多种功能的PDF文件处理工具
软件介绍 在日常办公和学习场景中,PDF文件使用极为频繁,而一款功能强大的PDF编辑软件能大幅提升处理效率。 今天要介绍的Adobe Acrobat Pro DC 2024.005.20414,就具备像编辑Word文档一样便捷编辑PDF的能力。 PDF文档在学习和工作中广泛应用…...

【SpringMVC】SpringMVC的启动过程与原理分析:从源码到实战
SpringMVC的启动过程与原理分析:从源码到实战 SpringMVC是Spring框架中用于构建Web应用的核心模块,它基于MVC(Model-View-Controller)设计模式,提供了灵活且强大的Web开发能力。本文将深入分析SpringMVC的启动过程、核…...
转自南京日报:天洑软件创新AI+仿真技术变制造为“智造
以下文章来源:南京日报 进入3月,南京天洑软件有限公司(以下简称天洑软件)董事长张明更加忙碌。“公司强调工业软件在数字经济与先进制造业融合中的关键作用,并已广泛应用在能源、电力和航空等领域。”他说,…...

golang dlv调试工具
golang dlv调试工具 在goland2022.2版本 中调试go程序报错 WARNING: undefined behavior - version of Delve is too old for Go version 1.20.7 (maximum supported version 1.19) 即使你go install了新的dlv也无济于事 分析得出Goland实际使用的是 Goland安装目录下dlv 例…...
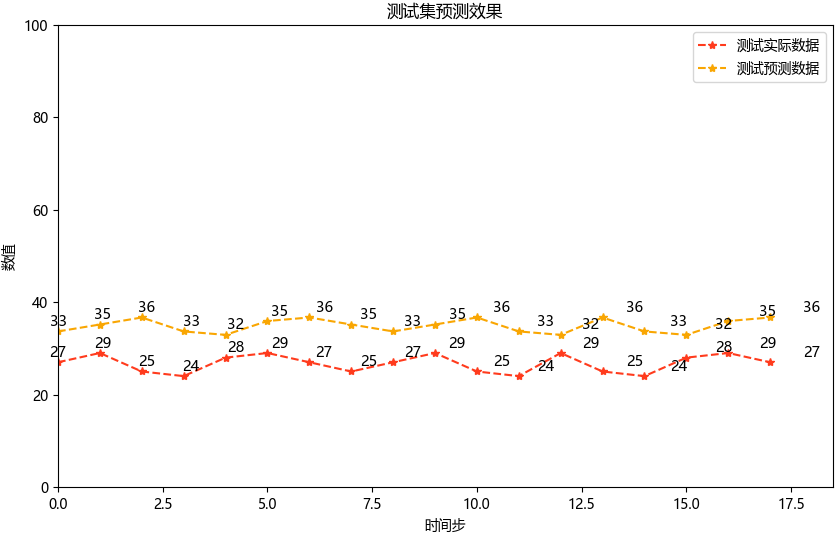
LSTM方法实践——基于LSTM的汽车销量时序建模与预测分析
Hi,大家好,我是半亩花海。本实验基于汽车销量时序数据,使用LSTM网络(长短期记忆网络)构建时间序列预测模型。通过数据预处理、模型训练与评估等完整流程,验证LSTM在短期时序预测中的有效性。 目录 一、实验…...
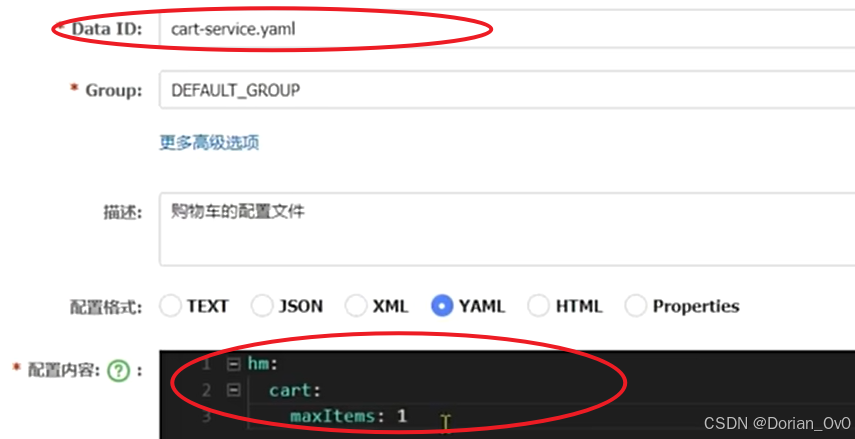
微服务——网关、网关登录校验、OpenFeign传递共享信息、Nacos共享配置以及热更新、动态路由
之前学习了Nacos,用于发现并注册、管理项目里所有的微服务,而OpenFeign简化微服务之间的通信,而为了使得前端可以使用微服务项目里的每一个微服务的接口,就应该将所有微服务的接口管理起来方便前端调用,所以有了网关。…...
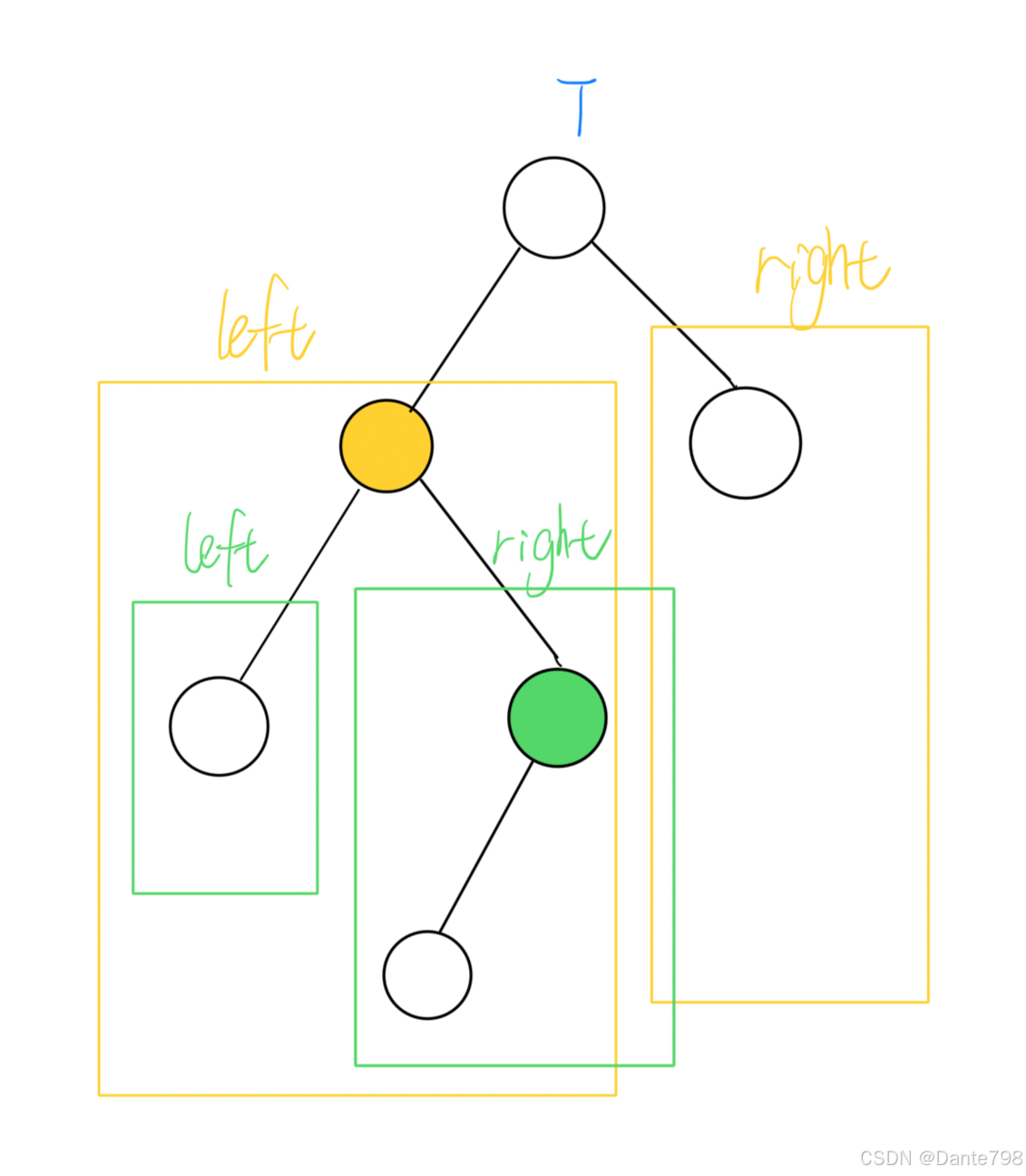
【数据结构】二叉搜索树、平衡搜索树、红黑树
二叉搜索树(Binary Search Tree) 二叉搜索树是一种特殊的二叉树,它用来快速搜索某个值,对于每个节点都应该满足以下条件: 若该节点有左子树,那么左子树中所有节点的值都应该小于该节点的值。若该节点有右…...

Spring Boot 解析 LocalDateTime 失败?Uniapp 传输时间变 1970 的原因与解决方案
目录 前言1. 问题分析2. 时间戳(推荐,可尝试)3. 使用 JsonDeserialize & JsonSerialize(中立)4. 前端传 ISO-8601 格式(不推荐,可尝试)5. 用 String(中立)…...
)
Xilinx ZYNQ FSBL解读:LoadBootImage()
篇首 最近突发奇想,Xilinx 的集成开发环境已经很好了,很多必要的代码都直接生成了,这给开发者带来了巨大便利的同时,也让人错过了很多代码的精彩,可能有很多人用了很多年了,都还无法清楚的理解其中过程。博…...

mysql中in和exists的区别?
大家好,我是锋哥。今天分享关于【mysql中in和exists的区别?】面试题。希望对大家有帮助; mysql中in和exists的区别? 1000道 互联网大厂Java工程师 精选面试题-Java资源分享网 在 MySQL 中,IN 和 EXISTS 都用于进行子查询,但它…...

oracle 数据导出方案
工作中有遇到需要将oracle 数据库表全部导出,还需要去除表数据中的换行符。 方案 shell 设计 封装函数 1 function con_oracle() 用于连接oracle 2 function send_file() 用于发送文件 3 主程序 使用循环将所有表导出并发送到数据服务器 主程序 程序代码 #!…...

Apache Commons Lang3 和 Commons Net 详解
目录 1. Apache Commons Lang3 1.1 什么是 Apache Commons Lang3? 1.2 主要功能 1.3 示例代码 2. Commons Net 2.1 什么是 Commons Net? 2.2 主要功能 2.3 示例代码 3. 总结 3.1 Apache Commons Lang3 3.2 Commons Net 3.3 使用建议 4. 参考…...
从0开始的操作系统手搓教程33:挂载我们的文件系统
目录 代码实现 添加到初始化上 上电看现象 挂载分区可能是一些朋友不理解的——实际上挂载就是将我们的文件系统封装好了的设备(硬盘啊,SD卡啊,U盘啊等等),挂到我们的默认分区路径下。这样我们就能访问到了ÿ…...

【Linux】36.简单的TCP网络程序
文章目录 1. TCP socket API 详解1.1 socket():打开一个网络通讯端口1.2 bind():绑定一个固定的网络地址和端口号1.3 listen():声明sockfd处于监听状态1.4 accept():接受连接1.5 connect():连接服务器 2. 实现一个TCP网络服务器2.1 Log.hpp - "多级日志系统"2.2 Daem…...

时序分析
1、基本概念介绍 1.1、 建立时间 T(su) 建立时间:setup time,它是指有效的边沿信号到来之前,输入端口数据保持稳定的时间。 1.1.1、 建立时间要求: 建立时间要求指的是 想要寄存器如期的工作,在有效时…...

doris:ClickHouse
Doris JDBC Catalog 支持通过标准 JDBC 接口连接 ClickHouse 数据库。本文档介绍如何配置 ClickHouse 数据库连接。 使用须知 要连接到 ClickHouse 数据库,您需要 ClickHouse 23.x 或更高版本 (低于此版本未经充分测试)。 ClickHouse 数据库的 JDBC 驱动程序&a…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...
)
华为OD最新机试真题-数组组成的最小数字-OD统一考试(B卷)
题目描述 给定一个整型数组,请从该数组中选择3个元素 组成最小数字并输出 (如果数组长度小于3,则选择数组中所有元素来组成最小数字)。 输入描述 行用半角逗号分割的字符串记录的整型数组,0<数组长度<= 100,0<整数的取值范围<= 10000。 输出描述 由3个元素组成…...
