LeetCode题目笔记——2563. 统计公平数对的数目
文章目录
- 题目描述
- 题目链接
- 题目难度——中等
- 方法一:排序+双指针
- 代码/Python
- 代码/C++
- 方法二
- 代码/Python
- 总结
题目描述
这是前天周赛的第二题。
统计公平数对的数目 - 给你一个下标从 0 开始、长度为 n 的整数数组 nums ,和两个整数 lower 和 upper ,返回 公平数对的数目 。
如果 (i, j) 数对满足以下情况,则认为它是一个 公平数对 :
- 0 <= i < j < n,且
- lower <= nums[i] + nums[j] <= upper
示例 1:
输入:nums = [0,1,7,4,4,5], lower = 3, upper = 6
输出:6
解释:共计 6 个公平数对:(0,3)、(0,4)、(0,5)、(1,3)、(1,4) 和 (1,5) 。
示例 2:
输入:nums = [1,7,9,2,5], lower = 11, upper = 11
输出:1
解释:只有单个公平数对:(2,3) 。
提示:
- 1 <= nums.length <= 105
- nums.length == n
- -109 <= nums[i] <= 109
- -109 <= lower <= upper <= 109
题目链接
题目难度——中等
方法一:排序+双指针
题目说需要统计公平数对的数目,而重点在于这个数目,一开始可能容易被误导将重点放在数对的下标i,j上面,仔细想想会发现我们只需要统计不同的数目就行,不用在乎具体的下标。所以我们可以先将数组排序,然后使用双指针,经过两次遍历,第一次我们统计一下满足上界upper的数对数目,第二次我们统计满足下界lower的数对数目。
具体的,第一次遍历时,两个指针一前一后,让p2=n-1,p1=0,如果两个数相加大于upper,我们就将p2左移一个位置,直到两个数相加<=upper,则此时从p1到p2之间的数,两两之和都会<=upper,也就有p2-p1个数对满足条件,然后再将p1右移,继续判断,直到p1与p2相遇。第一次遍历时我们只找到了满足上界的下标对,所以我们还要一次类似的遍历来减去多算的小于下界的数对。
代码/Python
class Solution:def countFairPairs(self, nums: List[int], lower: int, upper: int) -> int:nums.sort()n = len(nums)res = 0p1, p2 = 0, n - 1while p1 < p2:if nums[p1] + nums[p2] > upper:p2 -= 1else:res += p2 - p1p1 += 1p1, p2 = 0, n - 1while p1 < p2:if nums[p1] + nums[p2] < lower:res -= p2 - p1p1 += 1else:p2 -= 1return res

代码/C++
class Solution {
public:long long countFairPairs(vector<int>& nums, int lower, int upper) {long long res = 0;int p1, p2, n;sort(nums.begin(), nums.end());n = nums.size();p1 = 0;p2 = n - 1;while(p1 < p2){if(nums[p1] + nums[p2] > upper){p2--;}else{res += p2 - p1;p1++;}}p1 = 0;p2 = n - 1;while(p1 < p2){if(nums[p1] + nums[p2] < lower){res -= p2 - p1;p1++;}else{p2--;}}return res;}
};
方法二
前面既然已经排好序了,那么我们可以想想是否可以再利用这个有序的性质,比如二分查找。利用二分查找,来加速找到满足条件的下标对,实质上也是方法一的思路。这里贴一个灵茶大佬的题解:灵茶大佬
代码/Python
class Solution:def countFairPairs(self, nums: List[int], lower: int, upper: int) -> int:nums.sort()n = len(nums)res = 0for i, x in enumerate(nums):r = bisect_right(nums, upper - x, 0, i)l = bisect_left(nums, lower - x, 0, i)res += r - lreturn res
总结
方法一时间主要在前面排序上,O(NlogN),后面遍历是O(N),所以总的复杂度是(NlogN),空间复杂度 O(1) ,方法二在遍历里面有二分,所以应该是O(N·logN),空间是O(1)。
相关文章:

LeetCode题目笔记——2563. 统计公平数对的数目
文章目录题目描述题目链接题目难度——中等方法一:排序双指针代码/Python代码/C方法二代码/Python总结题目描述 这是前天周赛的第二题。 统计公平数对的数目 - 给你一个下标从 0 开始、长度为 n 的整数数组 nums ,和两个整数 lower 和 upper ,…...

【MySQL Shell】8.9.5 将集群重新加入到 InnoDB ClusterSet
如果 InnoDB 集群是 InnoDB ClusterSet 部署的一部分,MySQL Shell 会在重新启动后立即自动将其恢复到拓扑中的角色,前提是其运行正常且未被标记为无效。但是,如果集群被标记为无效或其 ClusterSet 复制通道已停止,则必须使用 clus…...

元素水平垂直居中的方法有哪些?如果元素不定宽高呢?
实现元素水平垂直居中的方式: 利用定位margin:auto利用定位margin:负值利用定位transformtable布局flex布局grid布局 1-利用定位margin:auto <style>.father{width:500px;height:300px;border:1px solid #0a3b98;position: relative;}.son{width:100px;heig…...

访问学者在新加坡访学生活日常花销大吗?
新加坡地理位置优越,社会发达,教学质量好,吸引不少国内学生前往新加坡留学、访学。那么,去新加坡访学,访问学者花销需要多少钱呢?下面和51访学网小编一起来了解一下吧。 一、饮食 新加坡的饮食从很亲民的…...
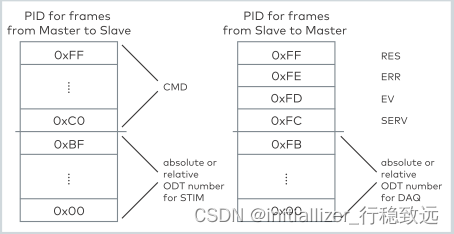
XCP实战系列介绍11-几个常用的XCP命令解析
本文框架 1.概述2. 常用命令解析2.1 CONNECT连接(0xFF)2.2 SHORT_UPLOAD 命令(0xF4)2.2 SET_MTA (0xF6)2.3 MOVE命令(0x19)2.4 GET_CAL_PAGE(0xEA)2.5 SET_CAL_PAGE(0xEB)2.6 DOWNLOAD(0xF0)1.概述 在文章《看了就会的XCP协议介绍》中详细介绍了XCP的协议,在《XCP实战系列介绍…...

全志V853芯片 如何在Tina V85x平台切换sensor?
目的 V85x某方案目前默认Sensor是GC2053。实际使用时若需要用到GC4663(比如wdr功能)和SC530AI(支持500W),可按如下步骤完成切换。 步骤 下面以GC4663为例,SC530AI按相应方式适配。 Step1 检查Sensor驱动…...
2023全网最火的接口自动化测试,一看就会
目录 接口自动化测试用例设计Excel接口测试用例访问MySQL接口测试用例访问PyTest测试框架接口自动化测试必备技能-HTTP协议request库实现接口请求 引言 与UI相比,接口一旦研发完成,通常变更或重构的频率和幅度相对较小。因此做接口自动化的性价比更高&…...
)
华为OD机试真题JAVA实现【最小传递延迟】真题+解题思路+代码(20222023)
🔥系列专栏 华为OD机试(JAVA)真题目录汇总华为OD机试(Python)真题目录汇总华为OD机试(C++)真题目录汇总华为OD机试(JavaScript)真题目录汇总文章目录 🔥系列专栏题目输入输出示例一输入输出说明解题思路核心知识点Code运行结果版权说...

Transformer
Transformer由4部分组成,分别是:输入模块、编码模块、解码模块、输出模块整体架构图:一、输入模块结构 (1)源文本嵌入层及其位置编码器(2)目标文本嵌入层及其位置编码器二、编码器模块结构由N个…...

并发包工具之 批量处理任务 CompletionService(异步)、CompletableFuture(回调)
文章目录一、处理异步任务并获取返回值——CompletionService二、线程池三、Callable 与 Future四、通过回调方式处理可组合编排任务——CompletableFuture一、处理异步任务并获取返回值——CompletionService 特点描述: 对于比较复杂的计算,把…...

验收测试分类
α测试 Alpha 是内测版本,即现在所说的CB。 此版本表示该软件仅仅是一个初步完成品, 通常只在软件开发者内部交流, 也有很少一部分发布给专业测试人员。 一般而言, 该版本软件的bug 较多, 普通用户最好不要安装。 β测试 Beta是公测版本,是对所有用户…...

因新硬件支持内核问题Ubuntu 22.04.2推迟发布
导读Ubuntu 22.04.2 LTS 原定于 2 月 9 日发布。但 Canonical 宣布该版本因各种问题不得不推迟两周,定于 2 月 23 日发布。 Ubuntu 22.04.2 LTS 原定于 2 月 9 日发布。但 Canonical 宣布该版本因各种问题不得不推迟两周,定于 2 月 23 日发布。 Canonica…...

agent扩展-自定义外部加载路径
自定义classLoader实现加载外部jar, 以skywalking agent 类加载器为例子 整体思路 扩展findClass ,解决loadClass可以查找到扩展findResource,解决getResources可以获取到资源 基本原理 ClassLoader loadClass的加载顺序 findLoadedClass 加载本地已经…...

Elasticsearch使用篇 - 指标聚合
指标聚合 指标聚合从聚合文档中提取出指标进行计算。可以从文档的字段或者使用脚本方式进行提取。 聚合统计可以同时返回明细数据,可以分页查询,可以返回总数量。 可以结合查询条件,限制数据范围,结合倒排索引列式存储。 指标…...

Python生命周期及内存管理
文章目录 一、Python的生命周期 1、概念2、如何监听生命周期二、内存管理 1.存储2.垃圾回收3.引用计数一、生命周期: 1、概念:一个对象从创建到消亡的过程 当一个对象呗创建是,会在内存中分配响应的内存空间进行存储 当这个对象不再使…...
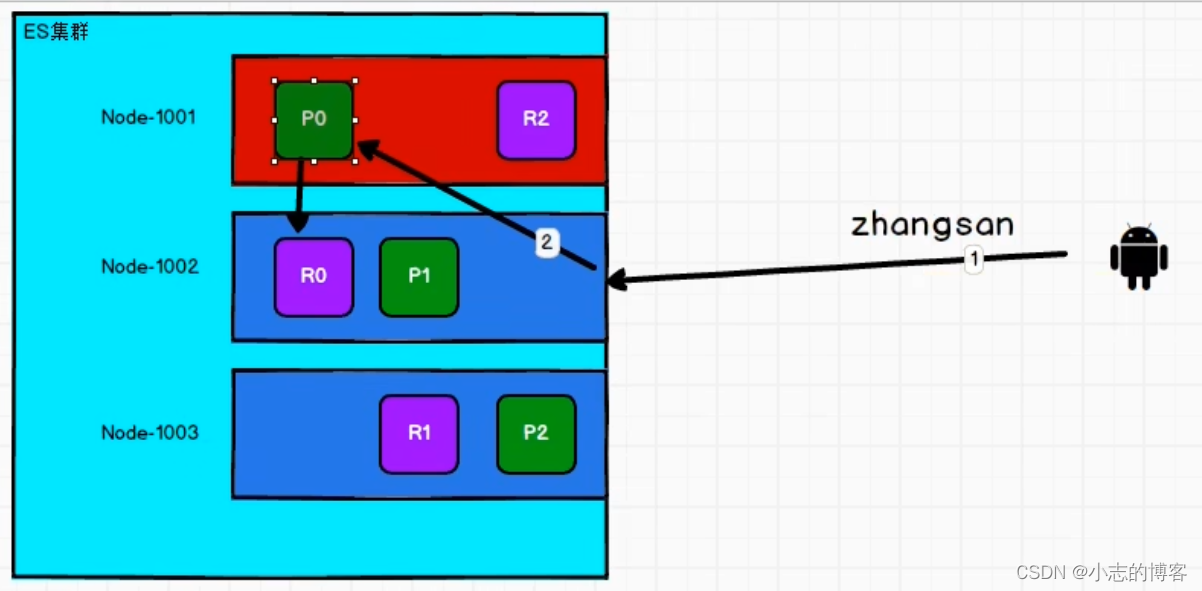
Elasticsearch7.8.0版本进阶——数据写流程
目录一、数据写流程概述二、数据写流程步骤2.1、数据写流程图2.2、数据写流程步骤(新建索引和删除文档所需要的步骤顺序)2.3、数据写流程的请求参数一、数据写流程概述 新建、删除索引和新建、删除文档的请求都是写操作, 必须在主分片上面完…...
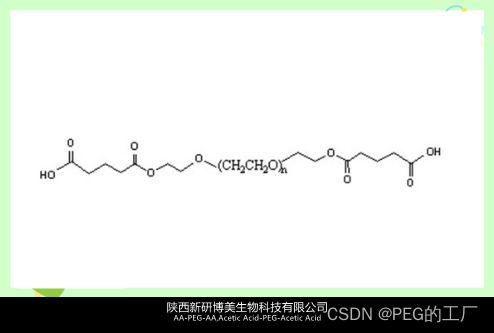
化学试剂Glutaric Acid-PEG-Glutaric Acid,GA-PEG-GA,戊二酸-聚乙二醇-戊二酸
一:产品描述 1、名称 英文:Glutaric Acid-PEG-Glutaric Acid,GA-PEG-GA 中文:戊二酸-聚乙二醇-戊二酸 2、CAS编号:N/A 3、所属分类:Carboxylic acid PEG 4、分子量:可定制, 戊…...

知识图谱业务落地技术推荐之国内知识图谱平台汇总(竞品)[阿里、腾讯、华为等】
各位可以参考国内知识图谱平台产品进行对技术链路搭建和产品参考提供借鉴。...
ABC 289 G - Shopping in AtCoder store 数学推导+凸包
大意: n个顾客,每个人有一个购买的欲望bi,m件物品,每一件物品有一个价值ci,每一个顾客会买商品当且仅当bici>定价. 现在要求对每一个商品定价,求出它的最大销售值(数量*定价) n,m<2e5 思路&#x…...

ARM Linux 如何在sysfs用户态命令行中控制 GPIO 引脚?
ARM Linux 如何在sysfs用户态命令行中控制 GPIO 引脚?我们在开发工作中,经常需要确定内核gpio驱动,是否有异常,或者在没有应用的情况下,像控制某个外设,这时我们就可以在控制台命令行中,用命令导…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...
