【人工智能】对贝叶斯网络进行吉布斯采样
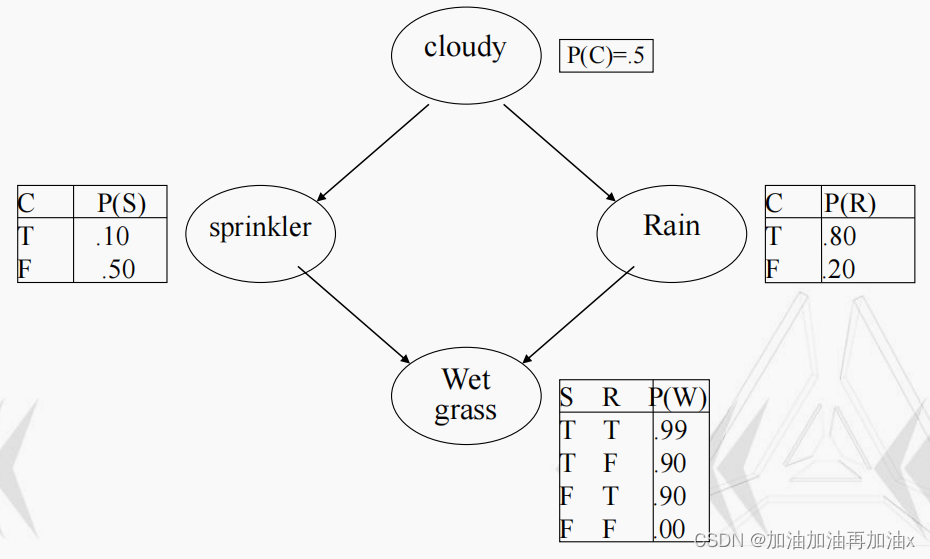
问题
现要求通过吉布斯采样方法,利用该网络进行概率推理(计算 P(R=T|S=F, W=T)、P2(C=F|W=T)的概率值)。
原理
吉布斯采样的核心思想为一维一维地进行采样,采某一个维度的时候固定其他的维度,在本次实验中,假定上一个采样的样本为<C(True)、S(False)、R(True)、W(False)>,此时对C维度进行采样,吉布斯采样将会利用 P(C|S=False,R=True,W=False)的分布得到一个新的 C的值(False),并将该值代替原先的值产生一个新的样本<C(False)、S(False)、R(True)、W(False)>。
给定分布π(C,S,R,W)
step 1. t=0 时刻产生一个初始状态<C0,S0,R0,W0>,count = 0,采样序列 x=[<C0,S0,R0,W0>]
step 2. 从条件概率分布 P(C|S0,R0)采样得到<C1,S0,R0,W0>,加入到 x[C 已知跳转下一步]
step 3. 从条件概率分布 P(S|C1,R0,W0)采样得到<C1,S1,R0,W0>,加入到 x[S 已知跳转下一步]
step 4. 从条件概率分布 P(R|C1,S1,W0)采样得到<C1,S1,R1,W0>,加入到 x[R 已知跳转下一步]
step 5. 从条件概率分布 P(W|S1,R1)采样得到<C1,S1,R1,W1>,加入到 x[W 已知跳转下一步]
step 6. count = count + 1,如果 count < 指定采样次数跳转到 step2
step 7. 在采样序列中统计满足条件的样本数量,除以总采样数即为所求。
数据结构使用一个 4*2*2*2*2 的矩阵 M 用于存储条件概率分布。如 M[0,:,0,0,0]即表示
P(C|S=False,R=False,W=False)的分布,M[0,:,1,0,0]表示P(C|S=True,R=False,W=False)的分布。该矩阵可通过给定的贝叶斯网络进行构建。
解答
# -*- coding:utf-8 -*-# Gibbs samplingimport numpy as np
import copyclass Gibbs:def __init__(self,query_id=1):self.x = []self.query_id = query_idassert query_id == 1 or query_id ==2self.tran_matrix = np.zeros((4,2,2,2,2))# 0 : C Cloudy# 1 : S Sprinkler# 2 : R Rain# 3 : W Wet grass# 计算条件概率分布# P(C) = 0.5self.tran_matrix[0] = 0.5 # P(C) = 0.5# P(S|C=T) = 0.1,P(S|C=F) = 0.5self.tran_matrix[1,1,0,:,:] = self.tran_matrix[0,1,0,:,:] * (1-0.1)self.tran_matrix[1,1,1,:,:] = self.tran_matrix[0,1,1,:,:] * 0.1self.tran_matrix[1,0,0,:,:] = self.tran_matrix[0,0,0,:,:] * (1-0.5)self.tran_matrix[1,0,1,:,:] = self.tran_matrix[0,0,1,:,:] * 0.5# P(R|C=T) = 0.8,P(R|C=F) = 0.2self.tran_matrix[2,1,:,0,:] = self.tran_matrix[1,1,:,0,:] * (1-0.8)self.tran_matrix[2,1,:,1,:] = self.tran_matrix[1,1,:,1,:] * 0.8self.tran_matrix[2,0,:,0,:] = self.tran_matrix[1,0,:,0,:] * (1-0.2)self.tran_matrix[2,0,:,1,:] = self.tran_matrix[1,0,:,1,:] * 0.2# P(W|S=T,R=T) = 0.99, P(W|S=T,R=F) = 0.9# P(W|S=F,R=T) = 0.9, P(W|S=F,R=F) = 0self.tran_matrix[3,:,1,1,0] = self.tran_matrix[2,:,1,1,0] * (1-0.99)self.tran_matrix[3,:,1,1,1] = self.tran_matrix[2,:,1,1,1] * 0.99self.tran_matrix[3,:,1,0,0] = self.tran_matrix[2,:,1,0,0] * (1-0.9)self.tran_matrix[3,:,1,0,1] = self.tran_matrix[2,:,1,0,1] * 0.9self.tran_matrix[3,:,0,1,0] = self.tran_matrix[2,:,0,1,0] * (1-0.9)self.tran_matrix[3,:,0,1,1] = self.tran_matrix[2,:,0,1,1] * 0.9self.tran_matrix[3,:,0,0,0] = self.tran_matrix[2,:,0,0,0] * (1-0)self.tran_matrix[3,:,0,0,1] = self.tran_matrix[2,:,0,0,1] * 0self.tran_matrix[0] = self.tran_matrix[3] / (self.tran_matrix[3].sum(axis=0,keepdims=True) + 1e-9)self.tran_matrix[1] = self.tran_matrix[3] / (self.tran_matrix[3].sum(axis=1,keepdims=True) + 1e-9)self.tran_matrix[2] = self.tran_matrix[3] / (self.tran_matrix[3].sum(axis=2,keepdims=True) + 1e-9)self.tran_matrix[3] = self.tran_matrix[3] / (self.tran_matrix[3].sum(axis=3,keepdims=True) + 1e-9)# 初始化样本if self.query_id == 1:# P(R=T|S=F,W=T)self.ignore_var_idx = [1,3] # S=F,W=Tself.x.append([True,False,True,True])else:# P(C=F|W=T)self.ignore_var_idx = [3] # W=Tself.x.append([True,False,True,True])self._sample_axis = 0self._var_num = 4def sample(self,sample_num:int):for _ in range(sample_num * (self._var_num - len(self.ignore_var_idx))):last_x = copy.copy(self.x[-1])sample_axis = self._next_sample_axis()last_x[sample_axis]=Truesample_prob = self.tran_matrix[sample_axis,int(last_x[0]),int(last_x[1]),\int(last_x[2]),int(last_x[3])]if np.random.rand() < sample_prob:last_x[sample_axis] = Trueelse:last_x[sample_axis] = Falseself.x.append(last_x)self.x = self.x[::self._var_num - len(self.ignore_var_idx)]def _next_sample_axis(self):self._sample_axis += 1self._sample_axis %= self._var_numwhile self._sample_axis in self.ignore_var_idx:self._sample_axis += 1self._sample_axis %= self._var_numreturn self._sample_axisdef calculate_ans(self):count = 0for x in self.x:if x[2] and self.query_id==1: count += 1if not x[0] and self.query_id==2: count += 1return count / len(self.x)def reset(self):self.x = self.x[:1]gibbs = Gibbs(1)
gibbs.sample(100)
ans = gibbs.calculate_ans()
gibbs.reset()
print('P(R=T|S=F,W=T)采样100次,结果为:',ans)
gibbs.sample(500)
ans = gibbs.calculate_ans()
gibbs.reset()
print('P(R=T|S=F,W=T)采样500次,结果为:',ans)
gibbs.sample(1000)
ans = gibbs.calculate_ans()
gibbs.reset()
print('P(R=T|S=F,W=T)采样1000次,结果为:',ans)gibbs = Gibbs(2)
gibbs.sample(100)
ans = gibbs.calculate_ans()
gibbs.reset()
print('P(C=F|W=T)采样100次,结果为:',ans)
gibbs.sample(500)
ans = gibbs.calculate_ans()
gibbs.reset()
print('P(C=F|W=T)采样500次,结果为:',ans)
gibbs.sample(1000)
ans = gibbs.calculate_ans()
gibbs.reset()
print('P(C=F|W=T)采样1000次,结果为:',ans)运行结果
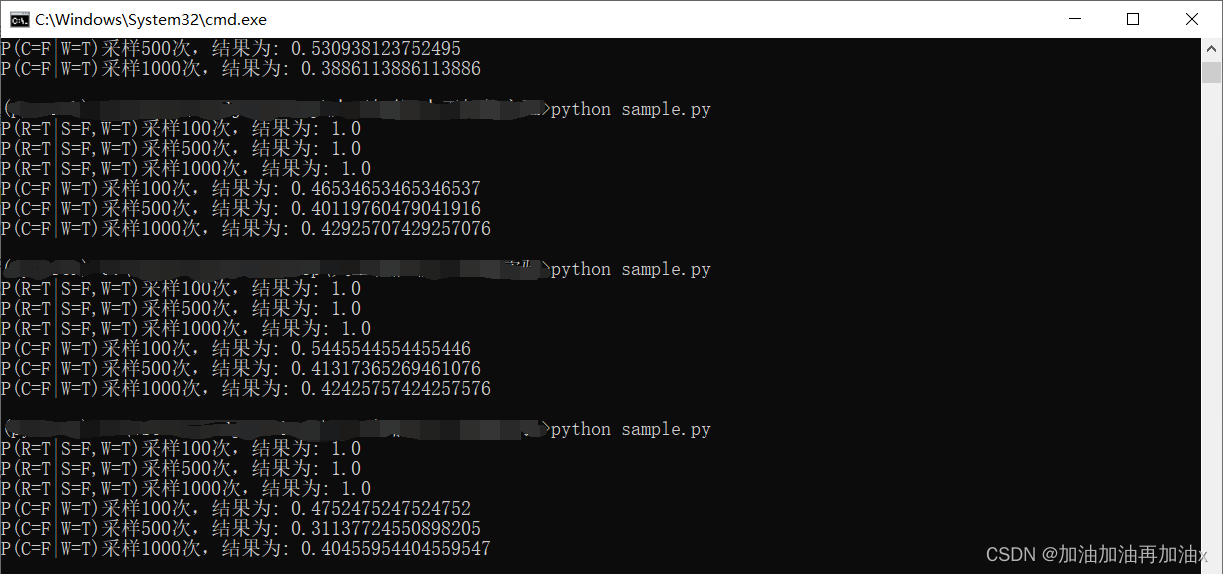
P(R=T|S=F, W=T)≈1
P(C=F|W=T)≈0.41
相关文章:

【人工智能】对贝叶斯网络进行吉布斯采样
问题 现要求通过吉布斯采样方法,利用该网络进行概率推理(计算 P(RT|SF, WT)、P2(CF|WT)的概率值)。 原理 吉布斯采样的核心思想为一维一维地进行采样,采某一个维度的时候固定其他的维度,在本次实验中,假…...
Java 面向对象基础
文章目录一、类和对象1. 类的定义2. 对象的使用二、对象内存图三、成员变量和局部变量四、封装1. private 关键字2. this 关键字五、构造方法六、标准类制作一、类和对象 在此之前,我们先了解两个概念,对象和类。 万物皆对象,客观存在的事物…...
—ConsumeMessageConcurrentlyService并发消费消息源码)
RocketMQ源码(21)—ConsumeMessageConcurrentlyService并发消费消息源码
基于RocketMQ release-4.9.3,深入的介绍了ConsumeMessageConcurrentlyService并发消费消息源码。 此前我们学习了consumer消息的拉取流程源码: RocketMQ源码(18)—DefaultMQPushConsumer消费者发起拉取消息请求源码RocketMQ源码(19)—Broker处理Default…...

基于 STM32+FPGA 的多轴运动控制器的设计
运动控制器是数控机床、高端机器人等自动化设备控制系统的核心。为保证控制器的实用性、实时性和稳定 性,提出一种以 STM32 为主控制器、FPGA 为辅助控制器的多轴运动控制器设计方案。给出了运动控制器的硬件电路设计, 将 S 形加减速算法融入运动控制器&…...
《爆肝整理》保姆级系列教程python接口自动化(十三)--cookie绕过验证码登录(详解
python接口自动化(十三)--cookie绕过验证码登录(详解 简介 有些登录的接口会有验证码:短信验证码,图形验证码等,这种登录的话验证码参数可以从后台获取的(或者查数据库最直接)。获取…...
soapui + groovy 接口自动化测试
1.操作excel的groovy脚本 package pubimport jxl.* import jxl.write.Label import jxl.write.WritableWorkbookclass ExcelOperation {def xlsFiledef workbookdef writableWorkbookdef ExcelOperation(){}//设置xlsFile文件路径def ExcelOperation(xlsFile){this.xlsFile x…...
:内存规整简介)
Linux内存管理(三十五):内存规整简介
源码基于:Linux5.4 0. 前言 伙伴系统以页面为单位来管理内存,内存碎片也是基于页面的,即由大量离散且不连续的页面组成的。从内核角度来看,出现内存碎片不是好事情,有些情况下物理设备需要大段的连续的物理内存,如果内核无法满足,则会发生内核错误。内存规整就是为了解…...
Java连接Redis
Jedis是Redis官方推荐的Java连接开发工具。api:https://tool.oschina.net/apidocs/apidoc?apijedis-2.1.0一、 导入包<!-- https://mvnrepository.com/artifact/redis.clients/jedis --> <dependency><groupId>redis.clients</groupId><…...
)
Python语言零基础入门教程(十六)
Python 模块 Python 模块(Module),是一个 Python 文件,以 .py 结尾,包含了 Python 对象定义和Python语句。 模块让你能够有逻辑地组织你的 Python 代码段。 把相关的代码分配到一个模块里能让你的代码更好用,更易懂。 模块能定…...
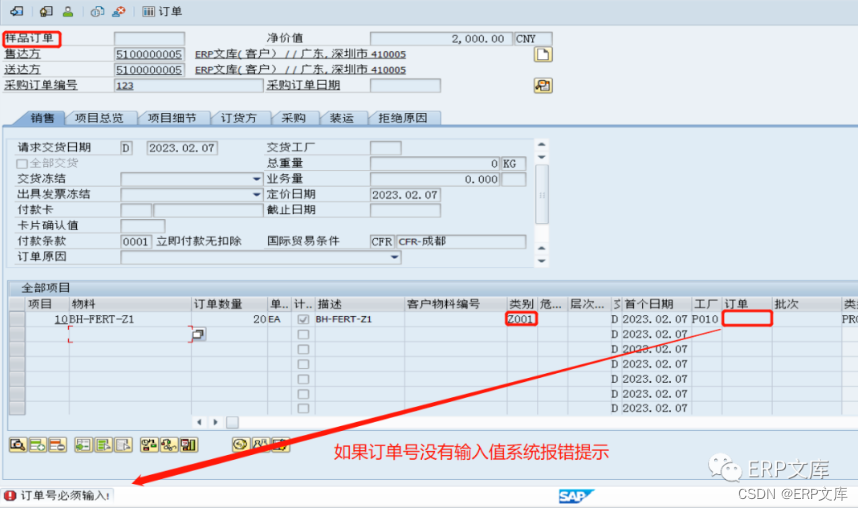
SAP ERP系统SD模块常用增强之一:VA01/VA02创建或修改SO的输入检查
在SAP/ERP项目的实施中销售管理模块(SD)的创建和修改销售订单必定会有输入字段校验检查的需求,来防止业务人员录入错误或少录入数据,SAP公司也考虑到这一点,所以这方面的配置功能也非常强大,通常情况下不需…...

深度学习知识补充
候选位置(proposal) RCNN 什么时ROI? 在图像处理领域,感兴趣区域(region of interest , ROI) 是从图像中选择的一个图像区域,这个区域是你的图像分析所关注的重点。圈定该区域以便进行进一步处理。使用ROI圈定你想读的目标&…...
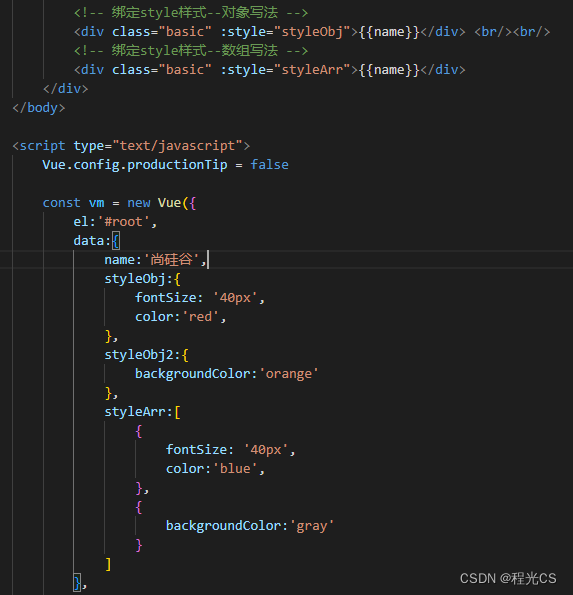
Vue笔记(1)——数据代理与绑定
一、初始Vue 1.想让Vue工作,就必须创建一个Vue实例,且要传入一个配置对象; 2.root容器里的代码依然符合html规范,只不过混入了一些特殊的Vue语法; 3.root容器里的代码被称为【Vue模板】; 4.Vue实例和容器是…...

LeetCode题目笔记——2563. 统计公平数对的数目
文章目录题目描述题目链接题目难度——中等方法一:排序双指针代码/Python代码/C方法二代码/Python总结题目描述 这是前天周赛的第二题。 统计公平数对的数目 - 给你一个下标从 0 开始、长度为 n 的整数数组 nums ,和两个整数 lower 和 upper ,…...

【MySQL Shell】8.9.5 将集群重新加入到 InnoDB ClusterSet
如果 InnoDB 集群是 InnoDB ClusterSet 部署的一部分,MySQL Shell 会在重新启动后立即自动将其恢复到拓扑中的角色,前提是其运行正常且未被标记为无效。但是,如果集群被标记为无效或其 ClusterSet 复制通道已停止,则必须使用 clus…...

元素水平垂直居中的方法有哪些?如果元素不定宽高呢?
实现元素水平垂直居中的方式: 利用定位margin:auto利用定位margin:负值利用定位transformtable布局flex布局grid布局 1-利用定位margin:auto <style>.father{width:500px;height:300px;border:1px solid #0a3b98;position: relative;}.son{width:100px;heig…...

访问学者在新加坡访学生活日常花销大吗?
新加坡地理位置优越,社会发达,教学质量好,吸引不少国内学生前往新加坡留学、访学。那么,去新加坡访学,访问学者花销需要多少钱呢?下面和51访学网小编一起来了解一下吧。 一、饮食 新加坡的饮食从很亲民的…...
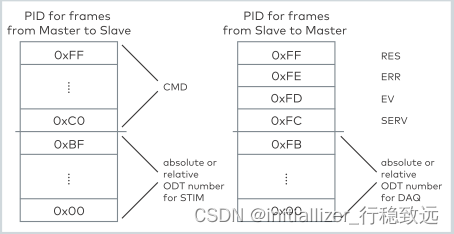
XCP实战系列介绍11-几个常用的XCP命令解析
本文框架 1.概述2. 常用命令解析2.1 CONNECT连接(0xFF)2.2 SHORT_UPLOAD 命令(0xF4)2.2 SET_MTA (0xF6)2.3 MOVE命令(0x19)2.4 GET_CAL_PAGE(0xEA)2.5 SET_CAL_PAGE(0xEB)2.6 DOWNLOAD(0xF0)1.概述 在文章《看了就会的XCP协议介绍》中详细介绍了XCP的协议,在《XCP实战系列介绍…...

全志V853芯片 如何在Tina V85x平台切换sensor?
目的 V85x某方案目前默认Sensor是GC2053。实际使用时若需要用到GC4663(比如wdr功能)和SC530AI(支持500W),可按如下步骤完成切换。 步骤 下面以GC4663为例,SC530AI按相应方式适配。 Step1 检查Sensor驱动…...
2023全网最火的接口自动化测试,一看就会
目录 接口自动化测试用例设计Excel接口测试用例访问MySQL接口测试用例访问PyTest测试框架接口自动化测试必备技能-HTTP协议request库实现接口请求 引言 与UI相比,接口一旦研发完成,通常变更或重构的频率和幅度相对较小。因此做接口自动化的性价比更高&…...
)
华为OD机试真题JAVA实现【最小传递延迟】真题+解题思路+代码(20222023)
🔥系列专栏 华为OD机试(JAVA)真题目录汇总华为OD机试(Python)真题目录汇总华为OD机试(C++)真题目录汇总华为OD机试(JavaScript)真题目录汇总文章目录 🔥系列专栏题目输入输出示例一输入输出说明解题思路核心知识点Code运行结果版权说...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...
