图的定义和基本术语
图的定义和基本术语
- 1.图的定义
- 2.图的基本术语
- 3.图的分类
1.图的定义
图是由顶点和有穷非空集合和顶点边的集合吗,表示为G=(V,E)。
G表示一个图,V是图G的顶点(数据元素)的集合,E是图G中顶点之间边的集合。在图中,顶点个数不能为零,但可以没有边。
2.图的基本术语
结点:图中的顶点
结点间的关系:图中顶点之间的连线
无向图:顶点之间的连线没有方向,用(v,w)表示
有向图:顶点之间的连线有方向,用 <v,w> 表示。v称为弧尾,w称为弧头。
v的入度:有向图中,以顶点v为弧头弧的数目。
v的出度:有向图中,以顶点v为弧尾弧的数目。
v的度:无向图中有光联的边;有向图中,出度和入度之和。
路径:从一个顶点到另一个顶点之间的路径。
路径长度:无向图,路径上边的数目就是长度;有向图,路径上权重之和就是长度。
简单路径:路径中的结点不重复。
简单回路:简单路径中第一个结点和最后一个结点是相同的一个顶点。
子图:边和顶点都是子集。
3.图的分类
1.从图中的方向性以及边上是否有权划分
有向图:边有方向无权。有向网:边有方向、有权。
无向图:边没有方向无权。无向网:边没有方向,有权
2.从图中的边(弧)数e和顶点数n之间的关系划分
无向完全图:对于n个顶点,任意两个顶点之间都有边,e=n * (n-1)/2
有向完全图:对于n的结点,任意结点都能直接互相到达,e=n * (n-1)
稀疏图:e <= nlogn
稠密图:e >nlogn
3.从连通性上划分
(1)无向图
连通性:若从顶点vi到顶点vj有路径,则称vi和vj连通。
连通图:任意两个结点都是连通。
连通分量:极大连通子图,含有极大顶点数(如果多加1个顶点,子图就不连通了)和依附于这些顶点的所有边。
(2)有向图
强连通性:从顶点vi到顶点vj有路径,则vj到vi也有路径。
强连通图:任意两个顶点都是强连通的。
强连通分量:极大强连通子图
(3)生成树和生成森林
生成树:极小连通子图,包含图中的全部顶点和连接全部顶点的n-1条边。如果多出一条边就出现回路。少一条边就非连通。生成树不唯一
生成森林:非连通图中存在若干个连通分量,每一个连通分量对于一棵生成树,这些连通分量的生成树组成了一个非连通图的生成树。
相关文章:

图的定义和基本术语
图的定义和基本术语1.图的定义2.图的基本术语3.图的分类1.图的定义 图是由顶点和有穷非空集合和顶点边的集合吗,表示为G(V,E)。 G表示一个图,V是图G的顶点(数据元素)的集合,E是图G中顶点之间边的集合。在图中…...

041:cesium加载Blue Marble地图
第041个 点击查看专栏目录 本示例的目的是介绍如何在vue+cesium中加载Blue Marble地图。Blue Marble是一个术语,用来描述星球漂浮在浩瀚太空中的形象。早在 1972 年,阿波罗 17 号任务的工作人员就首次捕捉到了地球的标志性卫星图像,并将其称为“Blue Marble”。从那时起,NA…...
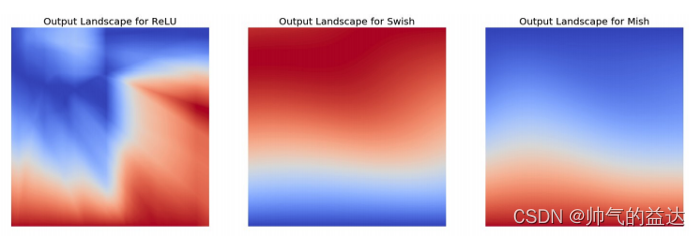
【概念梳理】激活函数
一、引言 常用的激活函数如下: 1、Sigmoid函数 2、Tanh函数 3、ReLU函数 4、ELU函数 5、PReLU函数 6、Leaky ReLU函数 7、Maxout函数 8、Mish函数 二、激活函数的定义 多层神经网络中,上层节点的输出和下层节点的输入之间具有一个函数关系,…...

【python】@property 和 @staticmethod
property 和 staticmethod 是 Python 中的两个装饰器,它们分别用于在类中创建属性或静态方法。它们的作用如下: property property:用于将类的一个方法作为属性访问。在 Python 中,使用“getter” 和“setter”方法来实现属性&a…...
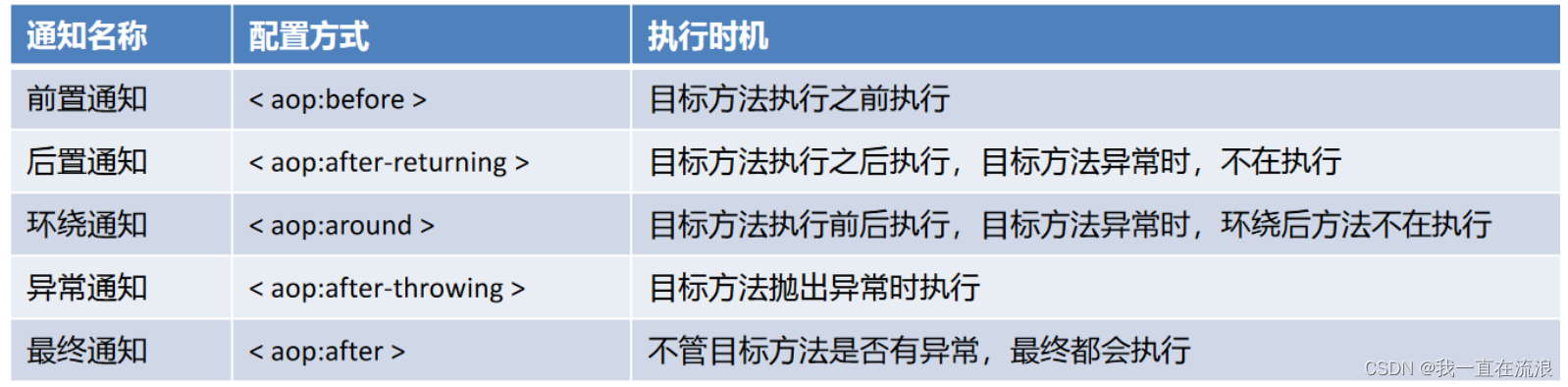
Spring题集 - Spring AOP相关面试题总结
文章目录01. Spring AOP 的理解?02. Spring AOP 思想的代码实现03. Spring AOP 的相关术语有哪些?04. Spring AOP 基于注解的切面实现?05. Spring AOP 的通知有哪些类型?06. AOP 有哪些实现方式?07. Spring AOP 和 AspectJ AOP 有…...

分考场
[蓝桥杯 2017 国 C] 分考场(假题:最小色数) 题目描述 nnn 个人参加某项特殊考试。 为了公平,要求任何两个认识的人不能分在同一个考场。 求最少需要分几个考场才能满足条件。 输入格式 第一行,一个整数 n(1<n<100)n(1<n<100…...

BI技巧丨DAX Studio
DAX Studio DAX Studio,作为PowerBI外部插件使用率排名第一的插件,相信各位小伙伴或多或少都听说过,那么DAX Studio具体有哪些功能呢? PS:DAX Studio的下载链接,小伙伴们可以自行搜索,这里就不…...

Java 8常用时间 API
Date: 你不爱我了吗? 🚡本地时间时区相关格式化在Java 8中,Instant类用于表示时间戳,相当于旧的Date类;LocalDateTime类用于表示日期和时间,相当于旧的Calendar类;DateTimeFormatter类用于格式化日期和时间…...

C++运算符
C运算符 运算符是一种告诉编译器执行特定的数学或逻辑操作的符号。C 内置了丰富的运算符,并提供了以下类型的运算符: 算术运算符关系运算符逻辑运算符位运算符赋值运算符杂项运算符 1. 算术运算符 运算符描述实例把两个操作数相加A B 将得到 30-从第…...

低/无代码赋能企业,IT与业务的角色正在悄然改变
现在这个社会,年轻人的压力是真的大,需要会的技能多到数不清。想学习多点技能也不知道去哪学,主要是网络资源太丰富,很难找到一个适合自己的。那接下来推荐4个大神级别的资源网站你可一定得码住,都是年轻人特别 …...

SpringCloud学习2(Spring Cloud Netflix)负载均衡Ribbon、Feign负载均衡、Hystix服务熔断
文章目录负载均衡RibbonRibbon的作用代码实现生产者cloud1_provider实现配置文件在HiController中编写以下代码启动集群消费者cloud1_consumer实现引入依赖编写配置文件编写启动类,并给RestTemplate配置LoadBalanced注解编写RestController来测试Feign负载均衡简介F…...
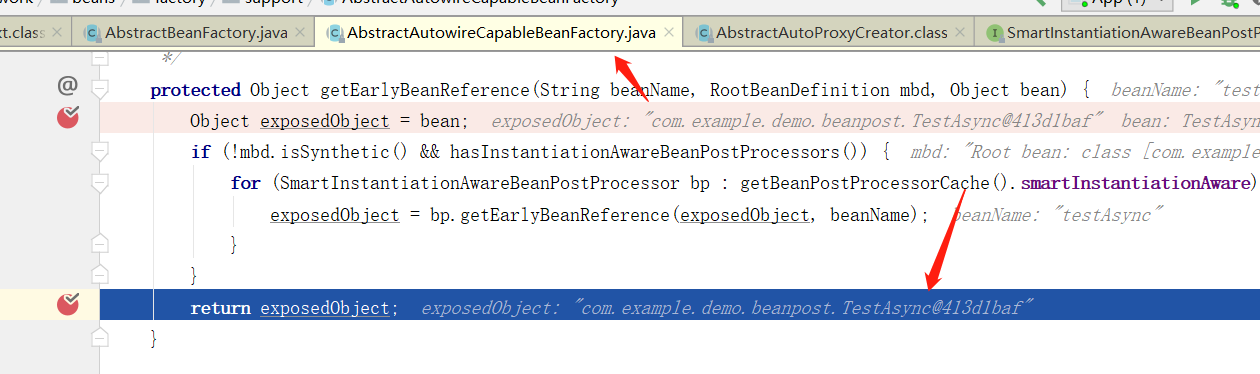
Spring 源码解析 - @Async 注解下的循环依赖问题原理
一、Async 注解下的循环依赖问题 我们都知道 Spring IOC 单例模式下可以帮助我们解决循环依赖问题,比如下面自己依赖自己循环依赖的场景: Component public class TestAsync {ResourceTestAsync async;public void test() {System.out.println("t…...

8个全球性编程比赛,天才程序员的梦想舞台
很多编程爱好者在学习之初,都渴望与全球的程序员一较高下,以证明自己的实力。 一些全球性的编程竞赛为他们提供了这样的机会,不仅可以与全世界的顶尖程序员们交流,还有机会获得丰厚的奖金和进入顶级公司的机会,更重要…...
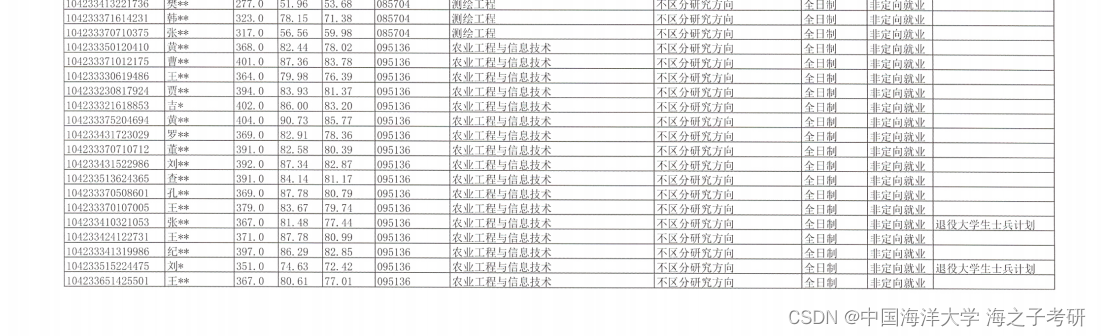
2023年中国海洋大学计算机及电子信息考研分析
考研时间跨度: 初试时间: 2022年8月23 海大推免及创新人才计划接收通知。 2022年9月13 海大专业目录及人数,包含推免。 2022年10月18 2022年硕士研究生计划 ,不含推免。 海大2022年硕士研究生计划 网上第一次时间为2022年9月24日…...

【C++笔试强训】第六天
选择题 1. 解析:十进制转换为八进制就是不断的除8,取余数。十进制转换成其他进制的数就是除以进制,取余。 解析:注意printf的转换,%%只会打印一个%,所以选A。 解析:由于()的原因p先和*结合&…...

Redission 中的 RedLock 原理实现, springboot 你造吗?
分布锁之RedLock 锁住你的心我的爱 🚂为什么需要使用 RedLock锁被误释放时钟不一致问题锁的“延迟释放”而不是死锁Redlock是啥redlock 存在什么问题惊群效应时钟漂移Redisson 实现 RedLock在 Redisson 中, RedLock的实现类是哪一个类?这一招叫抛砖引玉springboot …...

【沐风老师】3dMax一键房屋创建者插件使用方法详解
3dmax一键房屋创建者,一键生成墙体、窗洞和门洞的插件!这个脚本主要用于创建或捕获一些架构项目所代表的平面,这是通过导入它们并在每个所需的层添加值来实现的。传统方法,但是省事儿多了! 【版本要求】 3dMax 2015及…...

C/C++ 变量详解
文章目录前言一、静态变量与动态变量1. 概念2. 区别3. 使用方法和注意事项3.1 静态变量3.2 动态变量4. 结论二、全局变量与局部变量1. 区别2. 全局变量的使用方法和注意事项3. 局部变量的使用方法和注意事项4. 总结前言 对C学习感兴趣的可以看看这篇文章哦:C/C教程…...

新SSD盘安装操作系统启动不了
今天打算给电脑升级下装备,加装一块固态硬盘。 电脑原本自带两块硬盘(SSD128GSATA1T),SSD清理了许久还是没空间,于是就买了块1TSSD,打算扩容下。 打开电脑后盖傻眼了,没有备用插槽,…...

基于Spring、SpringMVC、MyBatis的病历管理系统
文章目录 项目介绍主要功能截图:登录首页医院公告管理用户管理科室信息管理医生管理出诊信息管理预约时间段管理预约挂号管理门诊病历管理就诊评价管理轮播图管理功能架构图部分代码展示设计总结项目获取方式🍅 作者主页:Java韩立 🍅 简介:Java领域优质创作者🏆、 简历…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...
