【ONE·Data || 常见排序说明】
总言
数据结构基础:排序相关内容。
文章目录
- 总言
- 1、基本介绍
- 2、插入排序
- 2.1、直接插入排序:InsertSort
- 2.1.1、单趟
- 2.1.2、总趟
- 2.2、希尔排序(缩小增量排序):ShellSort
- 2.2.1、预排序1.0:单组分别排序
- 2.2.2、预排序2.0:多组混合排序
- 2.2.3、加入直接排序3.0:对gap间距说明
- 3、选择排序
- 3.1、直接选择排序:SelectSort
- 3.2、堆排序:HeapSort
- 3.2.1、整体
- 3.2.2、向上调整函数、向下调整函数
- 4、交换排序
- 4.1、冒泡排序:BubbleSort
- 4.1.1、固定类型版本
- 4.1.2、多种类型版本
- 4.2、快速排序:QuickSort
- 4.2.1、Hoare法
- 4.2.1.1、单趟
- ①思路分析
- ②实现说明
- ③逻辑阐述
- 4.2.1.2、总趟:递归法
- ①相关实现与说明
- ②结果演示
- 4.2.2、挖坑法
- 4.2.2.1、单趟
- ①思路分析
- ②相关实现
- 4.2.2.2、总趟
- 4.2.3、前后指针法
- 4.2.3.1、单趟
- ①思路分析
- ②相关实现
- 4.2.3.2、总趟
- 4.2.4、快排优化1.0:关于key值的选取
- 4.2.5、快排优化2.0:小区间优化
- 4.2.6、快排:针对总趟的非递归写法
- 5、归并排序
- 5.1、递归版
- 5.2、非递归版
- 5.2.1、版本1.0
- 5.2.1.1、写法
- 5.2.1.2、问题
- 5.2.2、版本2.0
- 5.2.2.1、写法一
- 5.2.2.2、写法二
- 6、计数排序
1、基本介绍
| 常见排序 | 时间最坏 | 时间最好 | 空间 | 稳定性 | |
|---|---|---|---|---|---|
| 插入排序 | 直接插入排序 | O(N2) | O(N) | O(1) | √ |
| 希尔排序 | 平均 O(N1.3) | O(1) | × | ||
| 选择排序 | 直接选择排序 | O(N2) | O(N2) | O(1) | × |
| 堆排序 | O(N·logN) | O(N·logN) | O(1) | × | |
| 交换排序 | 冒泡排序 | O(N2) | O(N) | O(1) | √ |
| 快速排序 | O(N2) | O(N·logN) | O(logN) | × | |
| 其它排序 | 归并排序 | O(N·logN) | O(N·logN) | O(N) | √ |
2、插入排序
整体思想: 把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为止,得到一个新的有序序列 。
2.1、直接插入排序:InsertSort
1)、基本说明
直接插入排序的核心思路: 当插入第i(i>=1)i(i>=1)i(i>=1)个元素时,前面的array[0],array[1],…,array[i−1]array[0],array[1],…,array[i-1]array[0],array[1],…,array[i−1]已经排好序,此时用array[i]array[i]array[i]排序码与array[i−1],array[i−2],…array[i-1],array[i-2],…array[i−1],array[i−2],…的排序码顺序进行比较,找到正确的插入位置,将array[i]array[i]array[i]插入并将原来位置上的元素顺序后移。
说明: 给定一个数集将其排序,首先我们可以考虑对一个元素的排序,即单趟,再考虑对总体元素的排序,即多趟。
2.1.1、单趟
1)、思路分析
对于一个有序区间如何排序?(直接插入·单趟说明)
直接插入排序中,单趟是建立在原数集是有序区间的基础上的。即:默认[0,end]有序,新的需要插入的数在下标为end+1的位置,则插入后仍旧保持有序。
举例如下: 假设待排序区间如下图所示,假设排升序

其中经过前4趟后,使得[0,4]区间有序,下标为5的元素(即4)为当前趟待插入元素。那么按照直接插入排序的规则,将其与前[0,4]中元素比较,插入合适位置。

如下:4先与9比较,排升序,使得原先arr[4]中的元素(即9)后移,接下来4又与7比较。
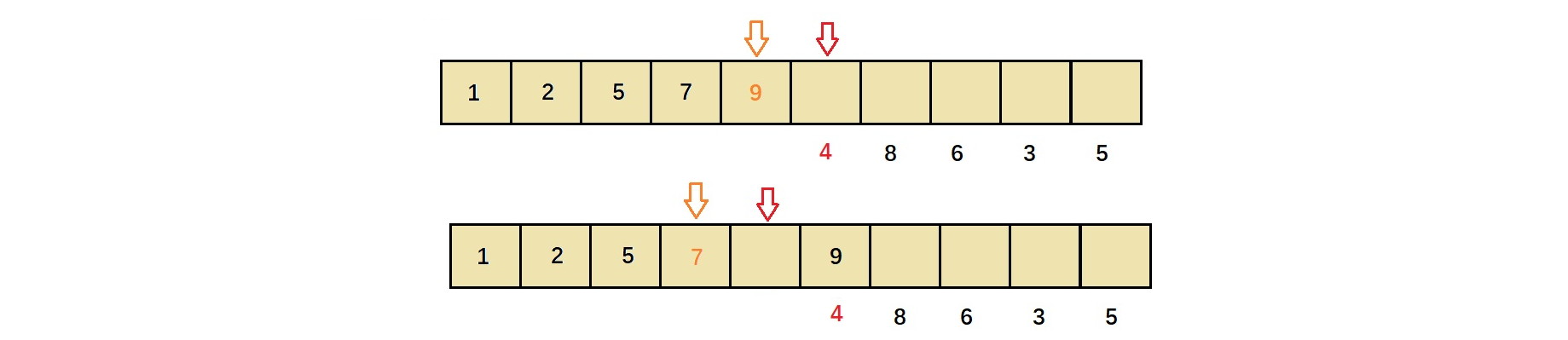
4与7比较,升序,4小,使得arr[3]中元素(即7)后移,接下来4与5比较。
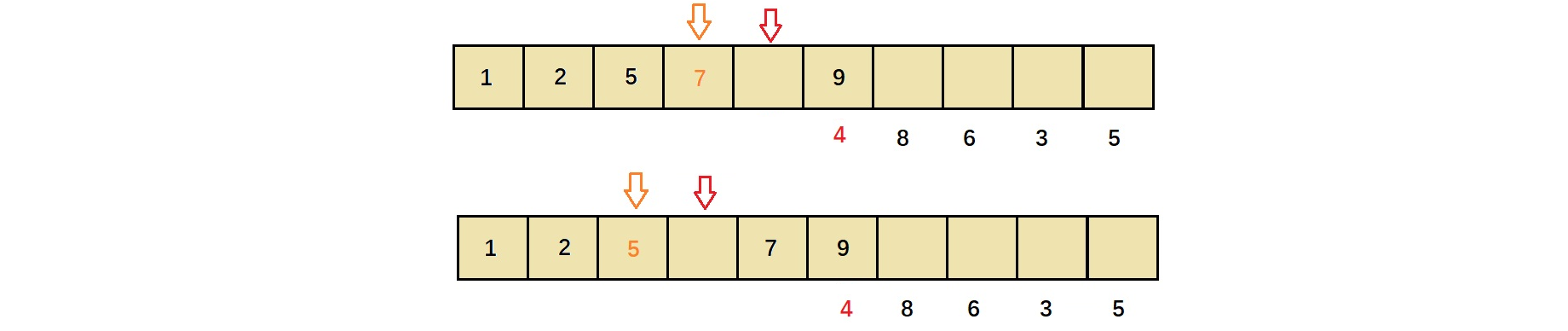
4与5比较,使得5后移,接下来4又与2比较
4与2比较,此时4比2大,则意味着arr[1]后位置为4的正确位置,将4放入。

2)、相关实现
int end;//默认[0,end]有序,待插入数在下标为end+1的位置int tmp = a[end + 1];//tmp用于保存当前趟中待插入数(原因:后续该位置会被覆盖)while (end >= 0){if (tmp < a[end]){a[end + 1] = a[end];//排升序:tmp需要放到end、end+1之间,即a[end]≤tmp≤a[end+1]end--;}elsebreak;//若不满足if条件,说明当前位置找到了,直接跳出}a[end + 1] = tmp;//再插入值
关于单趟中直接跳出原因说明:
当不满足if (tmp < a[end])条件时,说明找到待插入数正确位置,此时有两种情况。
情况一:待插入元素的位置在数组中间,该情况下end经过上一轮判断自减一次,实际插入位置为end+1。
情况二:数组原序列都比待插入元素大(小),此时end一直自减,直到为负数跳出while循环。此时实际插入位置相当于数组首位置,仍旧是end+1。

综合考虑,在跳出while循环后一并处理两种情况。
2.1.2、总趟
1)、思路分析
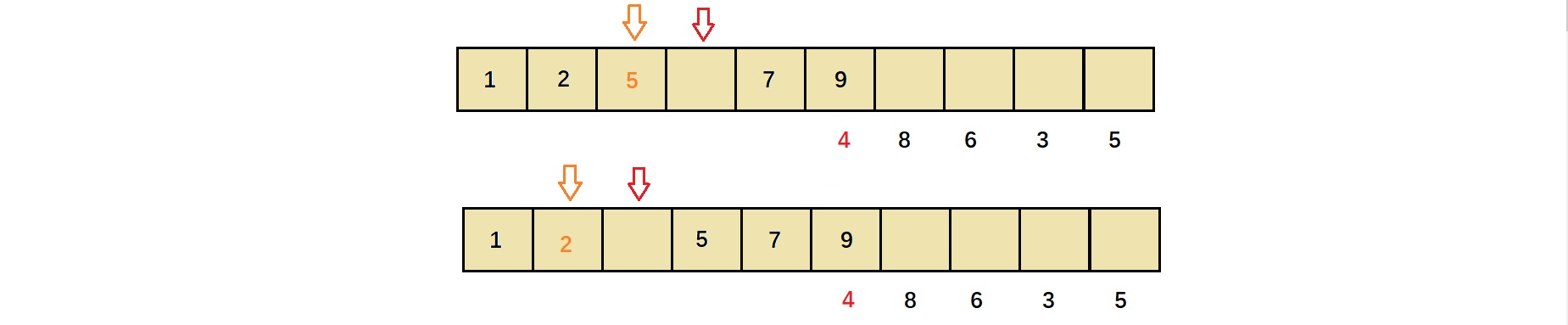
对于一个无序区间如何排序?(直接插入·总趟数说明)
我们只要定一个基准区间,后续元素视为待插入数据,依次迭代类推即可,如下图:
2)、相关实现
void InsetSort(int* a, int n)
{//总趟for (int i = 0; i < n-1; ++i)//默认end < n,end+1为插入数,因此end+1<n,即有end <n-1,i是用来控制end遍历总元素的。{//单趟int end=i;int tmp = a[end + 1];while (end >= 0){if (tmp < a[end]){a[end + 1] = a[end];end--;}elsebreak;}a[end + 1] = tmp;}
}
3)、相关验证

void Print(int* a, int n)
{for (int i = 0; i < n; ++i){printf("%d ", a[i]);}printf("\n");
}void test1()
{int arr[] = { 9,1,2,5,7,4,8,6,3,5 };int size = sizeof(arr) / sizeof(int);Print(arr, size);InsertSort(arr, size);Print(arr, size);}
2.2、希尔排序(缩小增量排序):ShellSort
1)、基本说明
希尔排序的核心思路: 对待排序文件,以gapgapgap为跨步,将所有数据分成nnn个组,所有距离为gapgapgap的数据分在同一组内,对每一组内的数据进行排序,重复上述分组和排序的工作,当到达gap=1gap=1gap=1时,所有记录在同一组内排好序。
整体上,希尔排序可分为两步骤:
1、预排序:使所排元素接近有序,提高了直接插入排序时的效率
2、直接插入排序:使上述元素达到有序
2.2.1、预排序1.0:单组分别排序
1)、思路分析
这里我们先来解决预排序问题:
对单组如何排序:
先设置gap值,将以下数据分组,例如gap=3。 对分在同组内的数据进行排序,其方法类似于直接插入排序,只不过这里我们比较的不是
对分在同组内的数据进行排序,其方法类似于直接插入排序,只不过这里我们比较的不是end和end+1,而是end和end+gap处的数据。
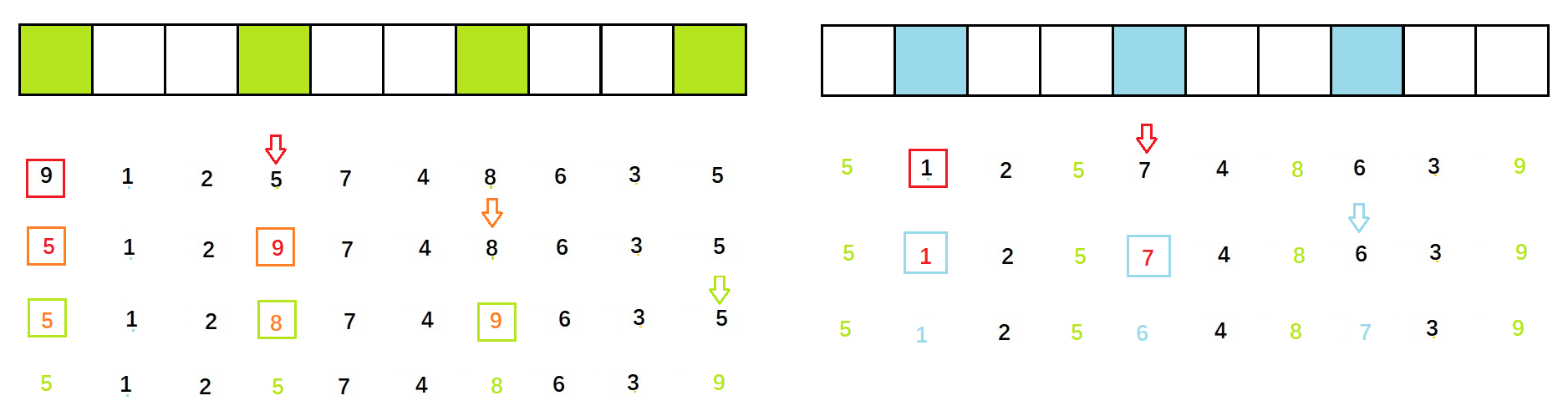
//单趟:其思路和直接插入排序类似,只是跨步由gap=1变为了任意正整数for (int i = 0; i < n - gap; i+=gap){int end=i;int tmp = a[end + gap];//此处tmp储存的是与end相距跨步为gap的元素:即同一组元素while (end >= 0){if (tmp < a[end])//排升序:当下标为end+gap的元素比下标为end所指向的元素还小时,将下标为end出的元素往后挪,挪到end+gap下标处{a[end + gap] = a[end];end -= gap;//注意此处end的跨步也要更改为gap}elsebreak;}a[end + gap] = tmp;}
对多组如何排序:
排完一组后对下一组进行排序,当所有组排完后,所得序列接近有序。
因此,我们只要在原先的单趟排序基础上,再嵌套一层循环,用于控制组数流动即可。
int gap = 3;for (int j = 0; j < gap; ++j)//多组间的流动{//单趟for (int i = 0; i < n - gap; i += gap){//……}}
2)、相关实现
上述思路整体实现如下:
void ShellSort_1(int* a, int n)
{int gap = 3;for (int j = 0; j < gap; ++j){//单趟for (int i = 0; i < n - gap; i += gap){int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}elsebreak;}a[end + gap] = tmp;}}}
进行验证:

void test2()
{int arr[] = { 9,1,2,5,7,4,8,6,3,5 };int size = sizeof(arr) / sizeof(int);Print(arr, size);ShellSort_1(arr, size);Print(arr, size);}
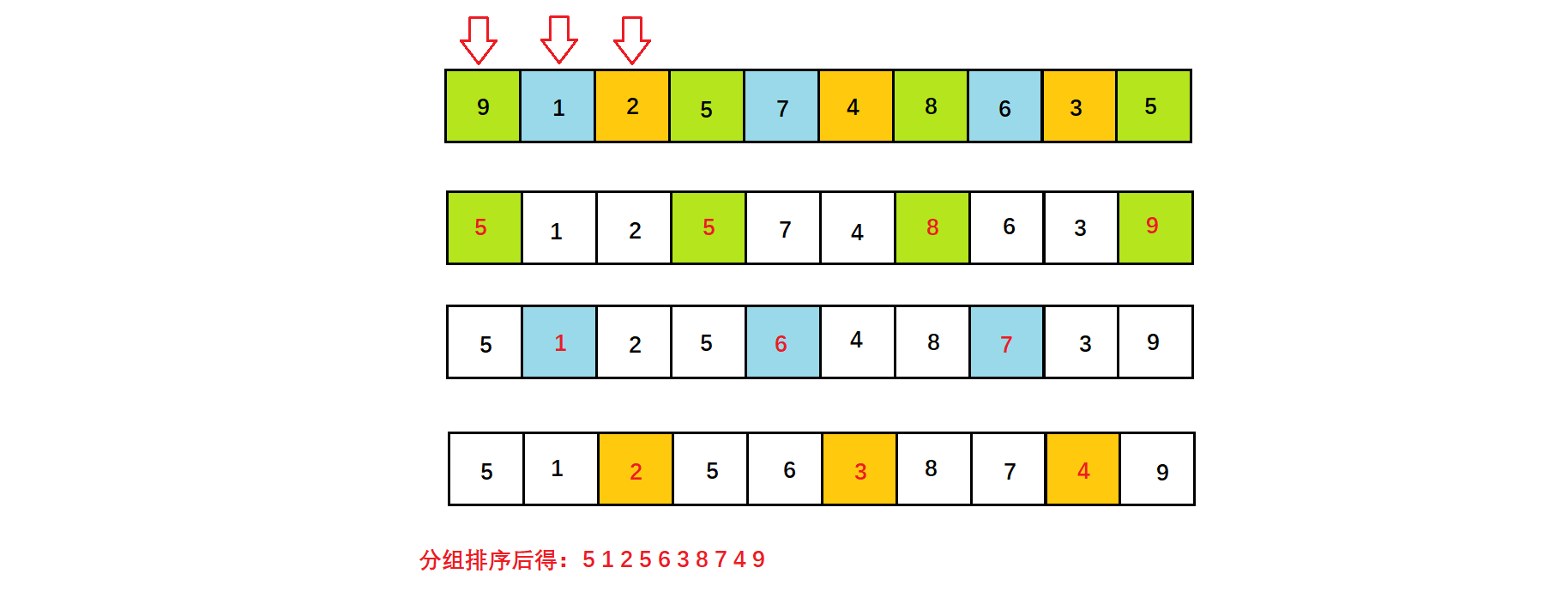
2.2.2、预排序2.0:多组混合排序
在上述代码中,我们嵌套了两层循环(j、i),实际上只需要做一些调整,用一次循环也能实现:
void ShellSort_2(int* a, int n)
{int gap = 3;for (int i = 0; i < n - gap; ++i)//若此处换为i++,则是多组元素轮番进行排序,即交替分组插入排序{int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}elsebreak;}a[end + gap] = tmp;}}
1.0:先在组内进行排序,整体排好后,再到下一组进行排序。
2.0:先对第一组内数据进行部分元素排序,来到下一组,同样进行部分排序,依此类推交替进行。
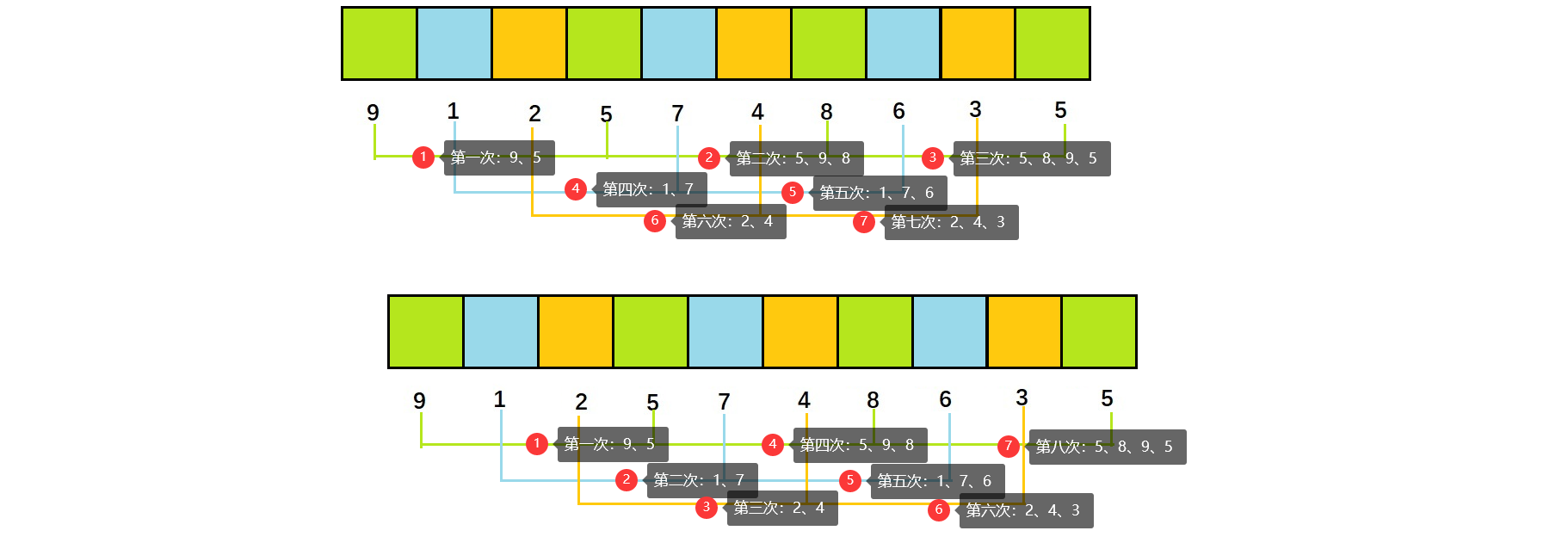
2.2.3、加入直接排序3.0:对gap间距说明
1)、思路分析
根据上述1.0、2.0内容,我们只是进行了预排序,将序列变得相对有序,要达到完全有序,还需要对gap间距做些调整,gap涉及到每次排序时的分组问题。
排升序,gap越大,大的数更快到后面,小的数更快到前面,但越不接近有序;
排升序,gap越小,越接近有序;
当gap=1时,就是直接插入排序。
那么,如何确定gap值,才能使得排序效果相对较优?
以下为一种给出的方案:
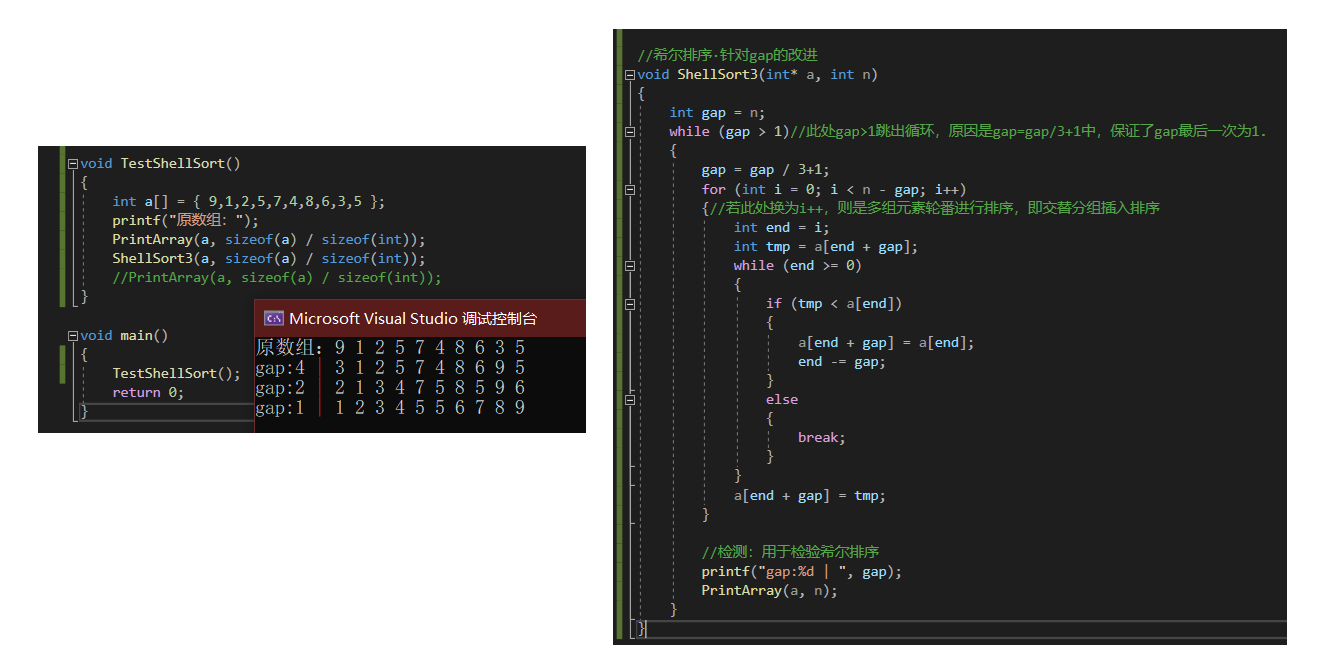
让gap成为一个动态的数int gap = n,从而达到多次预排的效果,并保证最后一次gap值为1gap = gap / 3 + 1,或者gap = gap / 2.
int gap = n;while (gap > 1)//此处gap>1循环继续,原因是gap=gap/3+1中,保证了gap最后一次为1.{gap = gap / 3 + 1;}
2)、相关实现
void ShellSort_3(int* a, int n)
{int gap = n;while (gap > 1)//此处gap>1跳出循环,原因是gap=gap/3+1中,保证了gap最后一次为1.{gap = gap / 3 + 1;for (int i = 0; i < n - gap; i++){//若此处换为i++,则是多组元素轮番进行排序,即交替分组插入排序int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}}
}
相关验证:gap=4、gap=2都在进行预排序,当gap=1时,直接插入排序。
3、选择排序
整体思想: 每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完 。
3.1、直接选择排序:SelectSort
1)、基本思路
直接选择排序思路说明:
在元素集合array[i]—array[n−1]array[i]—array[n-1]array[i]—array[n−1]中选择关键码最大(小)的数据元素,若它不是这组元素中的最后一个(第一个)元素,则将它与这组元素中的最后一个(第一个)元素交换。在剩余的array[i]—array[n−2](array[i+1]—array[n−1])array[i]—array[n-2](array[i+1]—array[n-1])array[i]—array[n−2](array[i+1]—array[n−1])集合中,重复上述步骤,直到集合剩余1个元素。
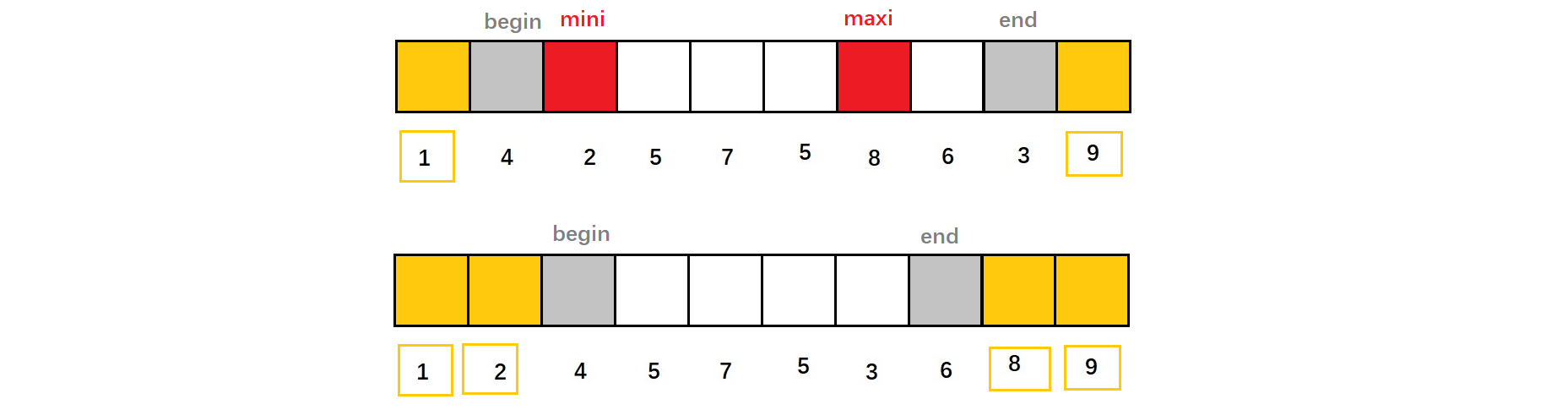
以上是直接选择排序的基本思路,换言之,在给定的数组区间[begin,end]中选出最小/最大元素,根据升序或降序要求,将其与首位元素交换。我们在此基础上做一些改动,同时找出区间[begin,end]内最小、最大值,同时与首位元素交化。这样单趟回合中,我们能排序好两个数,缩减[begin,end]区间范围,继续新一轮选择排序。
如下:单趟中,在区间[begin,end]范围内,找出本回合中最小、最大元素对应下标。

将最小、最大下标对应元素与begin、end下标对应元素交换,让最下、最大元素分别到数组两端。
缩减区间[begin,end],在新区间中重复上述操作,直至begin与end相遇(奇数时)或begin与end相错(偶数时)。
2)、代码实现
不完全写法1.0:
void SelectSort_1(int* a, int n)
{//begin、end代表数组下标,代表每趟[begin,end]int begin = 0;int end = n - 1;while (begin < end)//总共要走的次数{//单次操作int mini = begin, maxi = begin;//定义最小、最大值的下标,初始默认二者统一for (int i = begin; i <= end; ++i){//步骤一:找出单次操作中最小、最大元素对应下标//区间[begin,end]范围内,若有比下标为mini的元素更小的值,则更新mini的下标,同理,若有比下标为maxi的元素更大的值,则更新maxi的下标。if (a[i] < a[mini])mini = i;if (a[i] > a[maxi])maxi = i;}//步骤二:将最小、最大下标对应元素与begin、end下标对应元素交换,让最下、最大元素分别到数组两端Swap(&a[begin], &a[mini]);Swap(&a[end], &a[maxi]);//步骤三:缩减区间[begin,end],在新区间中重复上述操作begin++;end--;}
}
上述代码存在一个问题,需要注意一种特殊情况:
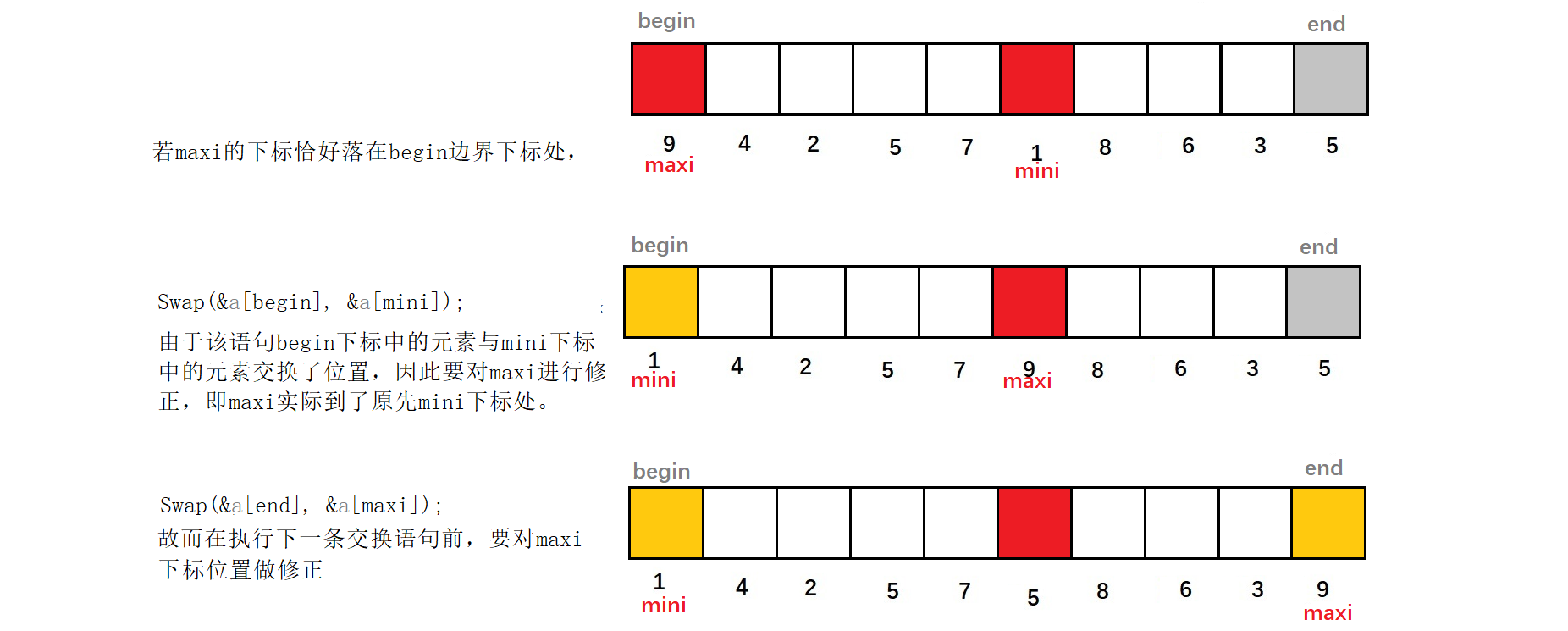
if (maxi == begin)//若maxi的下标表示的是begin下标,由于上述中begin下标中的元素与mini下标中的元素交换了位置,此处要对maxi进行修正maxi = mini;//相当于上述Swap(&a[begin], &a[mini])中把begin原先元素交换到了mini位置处,而begin对应的maxi指向没有随begin而变化,故在这里修正
修正写法2.0:
void SelectSort_1(int* a, int n)
{//begin、end代表数组下标,代表每趟[begin,end]int begin = 0;int end = n - 1;while (begin < end)//总共要走的次数{//单次操作int mini = begin, maxi = begin;//定义最小、最大值的下标,初始默认二者统一for (int i = begin; i <= end; ++i){//步骤一:找出单次操作中最小、最大元素对应下标//区间[begin,end]范围内,若有比下标为mini的元素更小的值,则更新mini的下标,同理,若有比下标为maxi的元素更大的值,则更新maxi的下标。if (a[i] < a[mini])mini = i;if (a[i] > a[maxi])maxi = i;}//步骤二:将最小、最大下标对应元素与begin、end下标对应元素交换,让最下、最大元素分别到数组两端Swap(&a[begin], &a[mini]);if (maxi == begin)//修正最大最小值在边界的情况maxi = mini;Swap(&a[end], &a[maxi]);//步骤三:缩减区间[begin,end],在新区间中重复上述操作begin++;end--;}
}
相关验证:

void test3()
{int arr[] = { 9,1,2,5,7,4,8,6,3,5 };int size = sizeof(arr) / sizeof(int);Print(arr, size);SelectSort_2(arr, size);Print(arr, size);
}
3.2、堆排序:HeapSort
3.2.1、整体
1)、基本说明
堆排序相关内容在其它博文有讲解,此处不做过多说明。堆排中注意整体实现顺序:1、建堆(两种方式);2、交换数据排序
二叉树相关:堆排
void HeapSort(int* a, int n)
{//建堆:方式一,自上而下,借助向上调整函数//时间复杂度:O(N*logN)for (int i = 1; i < n; i++){AdjustUp(a, i);}//建堆:方式二,自下而上,借助向下调整函数//时间复杂度:O(N)for (int i = (n - 1 - 1) / 2; i >= 0; --i){AdjustDwon(a, n, i);}//步骤二:排序,降序小堆,升序大堆int end = n - 1;//end,数组尾元素下标为n-1while (end > 0)//end!=0是因为堆顶自身交换及向下调整无意义{Swap(&a[0], &a[end]);//交换堆中首尾数据AdjustDwon(a, end, 0);//向下调整堆顶数据--end;//每次自减,即可把交换后的末位数排除在下一次向下调整中}
}
3.2.2、向上调整函数、向下调整函数
1)、向上调整函数
void Swap(HPDataType* n1, HPDataType* n2)
{HPDataType tmp = *n1;*n1 = *n2;*n2 = tmp;
}void AdjustUp(HPDataType*a,int child)
{HPDataType parent = (child - 1) / 2;while (child>0)//不断调整{//不满足堆的性质,交换,此处默认小堆if (a[child] < a[parent]){Swap(&a[child], &a[parent]);//交换//需要更改新增节点下标,进行下一轮父子关系判断child = parent;parent = (child - 1) / 2;}else{break;}}
}
2)、向下调整函数
void Swap(HPDataType* n1, HPDataType* n2)
{HPDataType tmp = *n1;*n1 = *n2;*n2 = tmp;
}void AdjustDown(HPDataType* a, int size, int parent)
{int child = parent * 2 + 1;//默认左孩子while (child<size){if (child + 1 < size && a[child + 1] < a[child])//比较两孩子:左孩子不满足,调整为右孩子child++;if (a[child] < a[parent])//父子节点比较,不满足堆性质,则交换{Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else//满足,则后续皆满足,退出循环{break;}}
}
4、交换排序
4.1、冒泡排序:BubbleSort
冒泡排序在C语言函数与数组、指针两篇博文中有介绍,此处也不做过多说明。
4.1.1、固定类型版本
void BubbleSort(int* a, int n)
{for (int j = 0; j < n - 1; ++j){int exchange = 1;for (int i = 0; i < n-j-1; ++i){if (a[i] > a[i + 1]){exchange = 0;Swap(&a[i], &a[i + 1]);}}if (exchange)break;}}
4.1.2、多种类型版本
void swap(char* num1, char* num2, size_t size)
{for (size_t i = 0; i < size; ++i){//一个字符一个字符的交换char tmp = *num1;*num1 = *num2;*num2 = tmp;//注意字符指针的迭代num1++;num2++;}
}void bubble_sort(void* base, size_t num, size_t size, int (*compar)(const void*, const void*))
{for (size_t i = 0; i < num - 1; ++i){for (size_t j = 0; j < num - 1 - i; ++j){//arr[j]>arr[j+1]if (compar((char*)base + size * j, (char*)base + size * (j + 1)) > 0)//排升序{swap((char*)base + size * j, (char*)base + size * (j + 1),size);//交换元素}}}
}
4.2、快速排序:QuickSort
一种二叉树结构的交换排序方法,其基本思想为:任取待排序元素序列中的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止。(排出来的是升序)
4.2.1、Hoare法
4.2.1.1、单趟
思路: 选出一个key,一般是最左边或者最右边的值。
单趟排序完成后,对于升序,要求达到左边比key小,右边比key大,对降序,要求达到左边比key大,右边比key小。
①思路分析
1)、思路分析
对于单趟(升序):
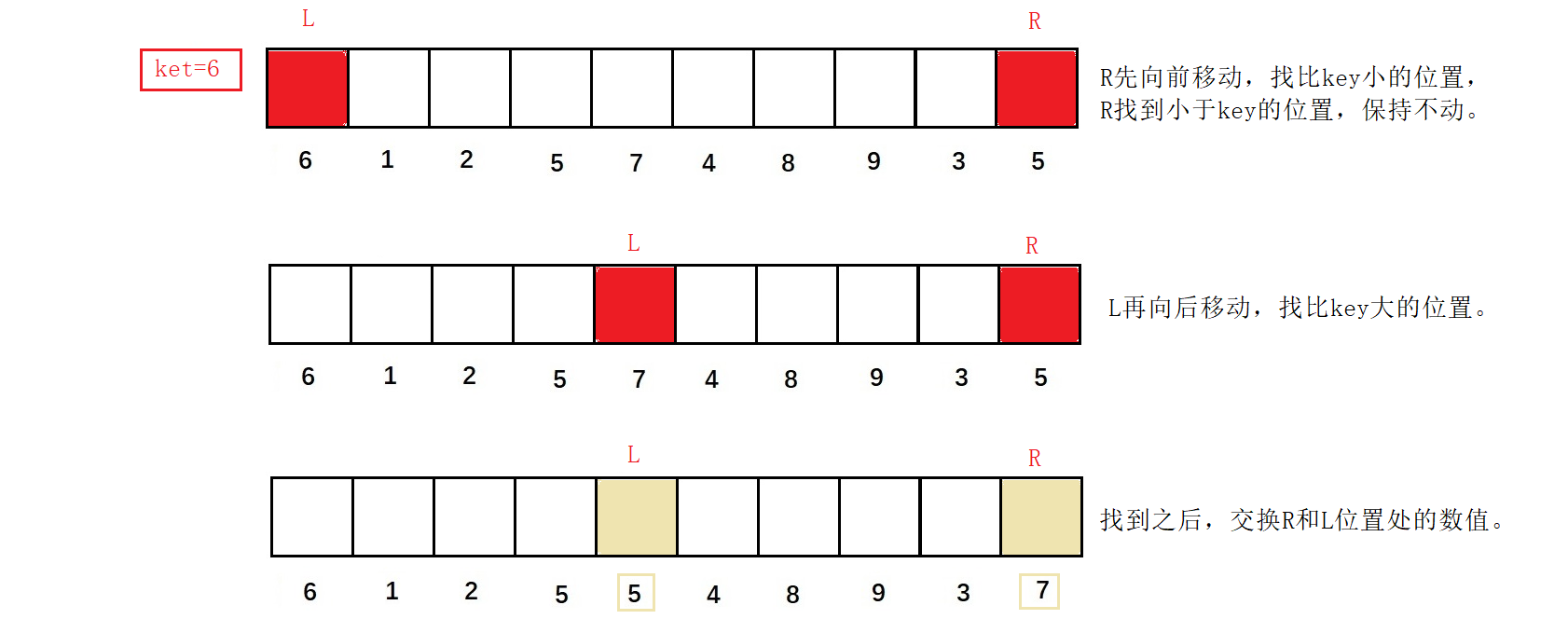
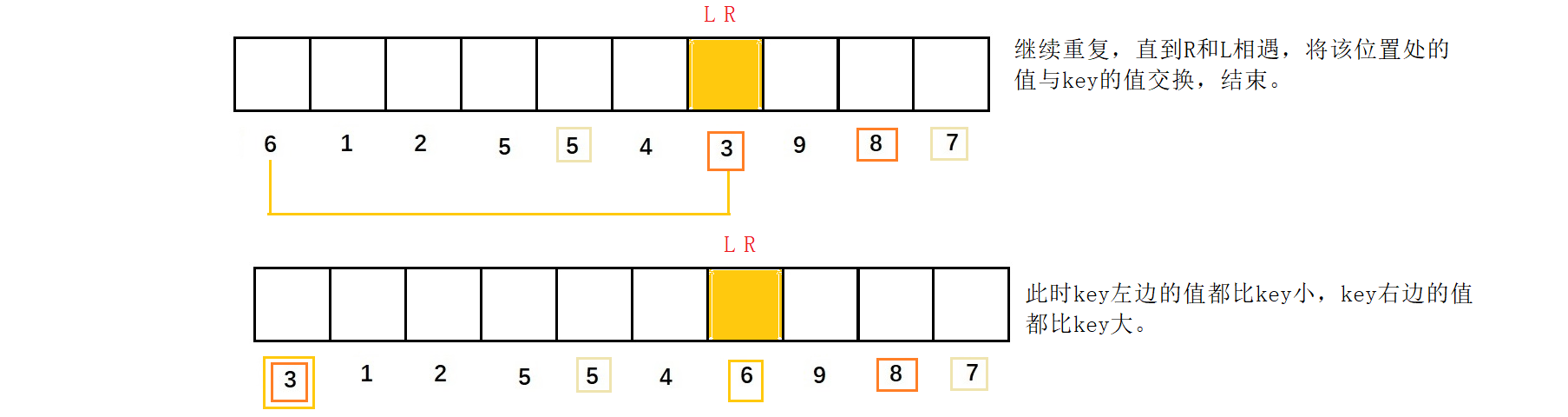
先以最左或最右位置选出一个key,设左为L,右为R。

若左为key,则R先向前移动,找比key小的位置,R找到小于key的位置,保持不动。L再向后移动,找比key大的位置。找到之后,交换R和L位置处的数值。
R再次向前移动,找比key小的位置,L向后移动,找比key大的位置,找到之后,交换R和L位置的数值。
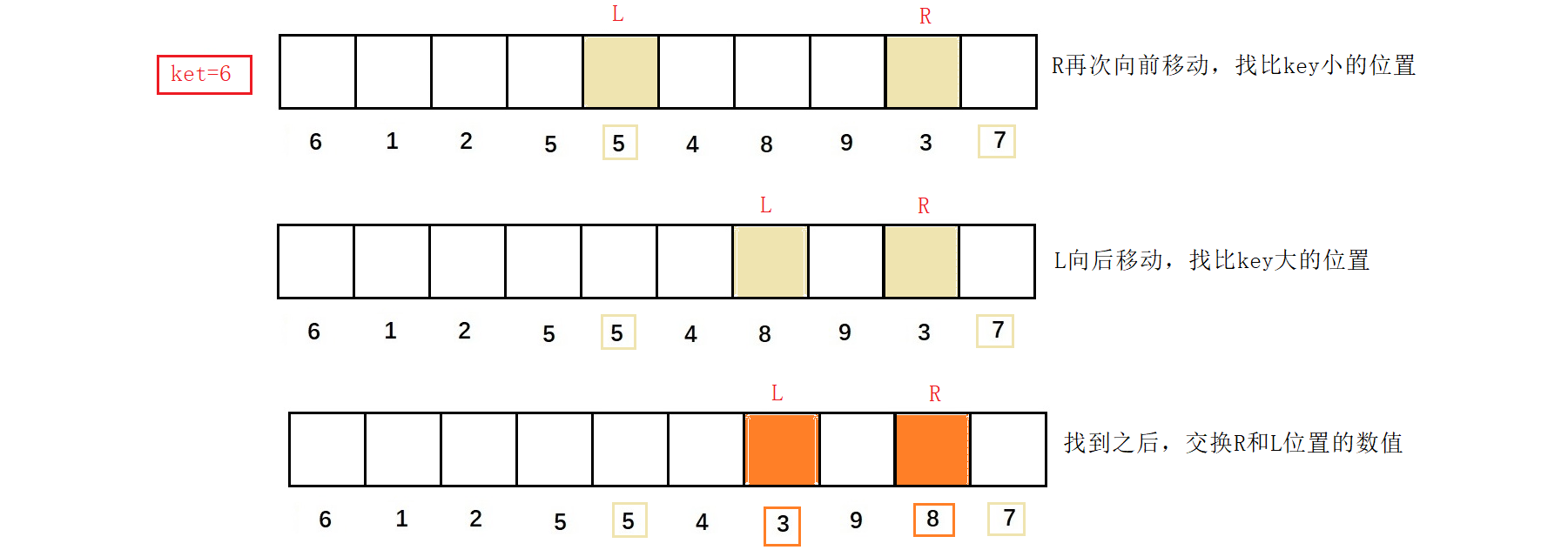
R继续向前找比key小的值,L继续向后找比key大的值,当R和L相遇,将该位置处的值与key的值交换结束。
此时key左边的值都比key小,key右边的值都比key大。
②实现说明
2)、相关实现
错误实现演示:
int left = 0, right = n - 1;int key = a[left];//选左为keywhile (left < right){//右先走,右找小while (a[right] > key)--right;//左后走,左找大while (a[left] < key)++left;//找到交换Swap(&a[left], &a[right]);}//交换最后的keySwap(&key, &a[left]);
问题一:a[right] > key、a[left] < key

修改如下:
//右先走,右找小while (a[right] >= key)--right;//左后走,左找大while (a[left] <= key)++left;
问题二:left < right

修改如下:
//右先走,右找小while (left < right && a[right] >= key)--right;//左后走,左找大while (left < right && a[left] <= key)++left;
问题三:Swap(&key, &a[left]);
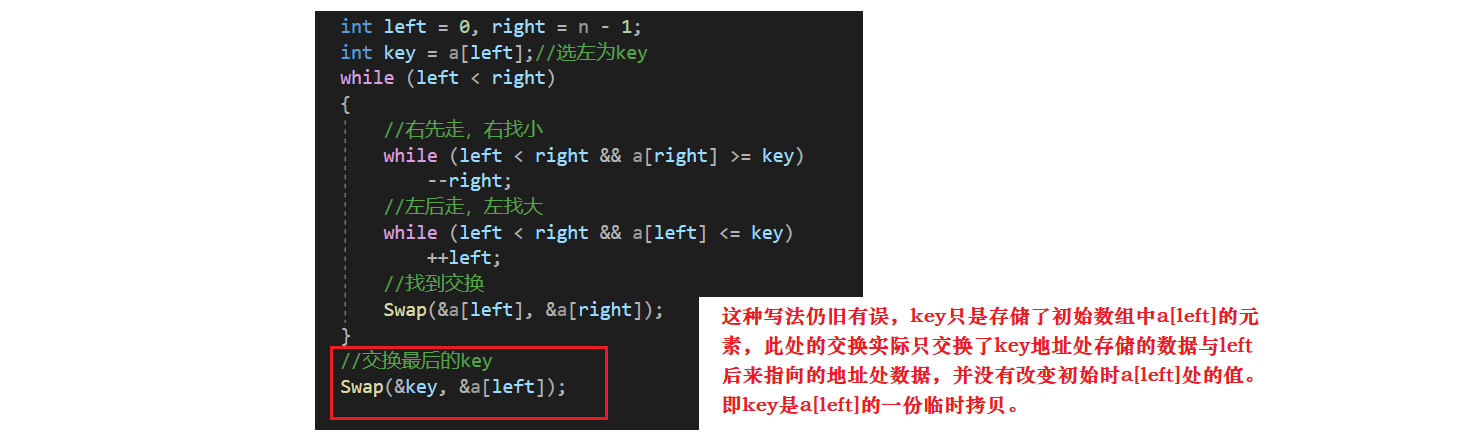
正确实现演示:
int left = 0, right = n - 1;int key = left;//选左为keywhile (left < right){//右先走,右找小while (left < right && a[right] >= a[key])--right;//左后走,左找大while (left < right && a[left] <= a[key])++left;//找到交换Swap(&a[left], &a[right]);}//交换最后的keySwap(&a[key], &a[left]);
③逻辑阐述
3)、相关问题说明
1、以升序为例,如何做到左边数值比key小,右边数值比key大?
回答:将左边比key大的值和右边比key小的值两两交换,这样左边只剩下原先比key小的值和被交换过来的比key小的值,右边与左边相反。
如此便达到升序的效果。如果要实现降序,只需要左边找小值,右边找大值即可。
2、关于左右L、R是否会错过问题?
回答:不会,L、R会错过的情况是二者同时一个向后一个向前遍历,因奇偶数的不同而导致相错问题。
while(left<right)
{++left; //从代码执行角度虽然在两行分先后,--right; //但二者从逻辑角度发生在同一时刻(同语句中)
}
但此处L、R并非同时进行,是一个先完成它的步数,另一个再完成对应步数,由于二者相向,故一定会有L=R相遇时。
while (left < right && a[right] >= a[key])--right; //右边先走,右边while结束后,right不动while (left < right && a[left] <= a[key])++left; //此时左边在走
3、左边做key,为什么要让右边先走?(反之,右边做key,为什么要让左边先走?)
回答: 对于升序,左边做key右边先走,可保证相遇时的值比key小或者与key相等(右边做key左边先走,可保证相遇时的值比key大,或者与key相等)
分析: 以升序、左边做key右边先走为例子
情形一: R先走,R停下,L去遇到R(L停下只有两种可能:①L找到对应值停下,②L与R相遇,此处是②,因为①的情况L停下未遇到R)。
此时相遇的位置是R停下的位置,而要使R停下,即有a[R]<a[key]。相遇交换就使得小于key的值到左边去。
情形二: R先走,R没有找到比key要小的值,但R遇到了L。
子情形一,最初始的一轮循环中,R往前走直接到达key处(即L没有机会往后走),此时说明key后的数组元素都比key大,LR相遇点的值即上述中与key相等的情况。
子情形二,L、R经过彼此交换后的下一组循环中,R往前走直接遇到了L,说明在(L,R]区间内的元素都比key大,而L(与R的相遇点)处的值是上一轮循环后经过交换的值,即上一轮R中小于key的值此时在下一轮循环L位置处(L在R后变动)。
4.2.1.2、总趟:递归法
①相关实现与说明
单趟排序完成,以key为界,数组被分为三个区间。[begin,key-1]区间内数据比key小 、key 、[key+1,end]区间内数据比key大。
此时我们再分别对两区间数据重复上述单趟操作即可。这有点类似于二叉树的前序遍历。
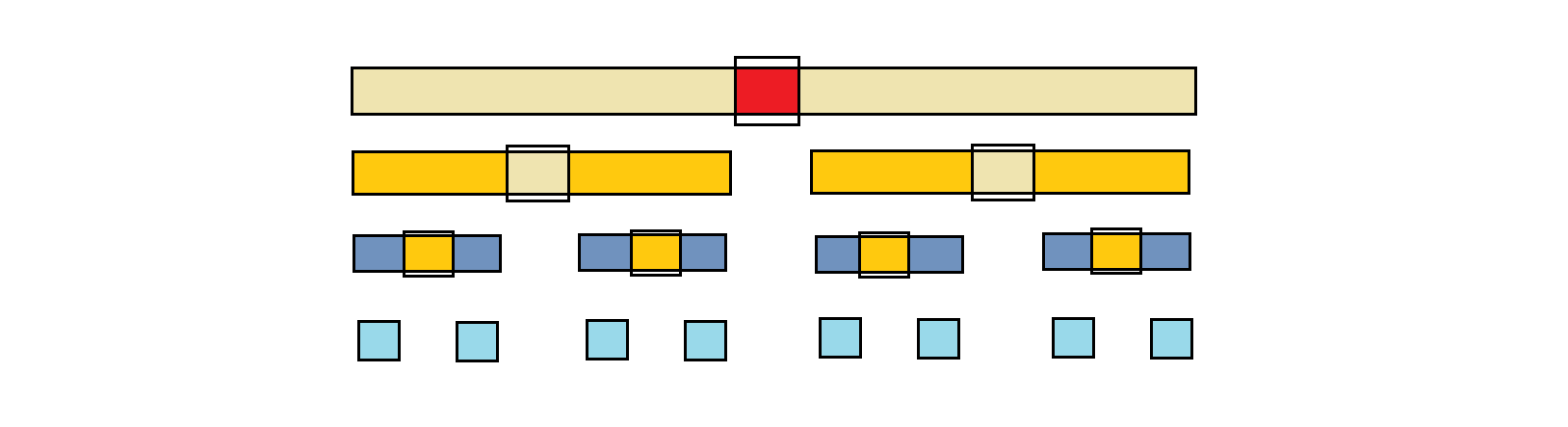
这里我们将上述快排中单趟取出单独封装为一个函数:
以[begin,end]作为单趟区间,这样我们只用修改begin,end具体指向下标,就能让其达成前序遍历,也就是快排中的总趟。
int PartSort(int* a, int begin, int end)
{int left = begin, right = end;int key = left;//选左为keywhile (left < right){//右先走,右找小while (left < right && a[right] >= a[key])--right;//左后走,左找大while (left < right && a[left] <= a[key])++left;//找到交换Swap(&a[left], &a[right]);}//left、right相遇时,将key处的数据与left处的数据交换Swap(&a[key], &a[left]);key = left;//Swap交换了key原先下标元素return key;
}
return key;,返回key值,是为了下述总趟排序时,方便寻找各子区间位置。[begin,key-1]、key、[key+1,end]
总趟如下:
void QuickSort(int* a, int begin, int end)
{if (begin >= end)return;int key = PartSort(a, begin, end);QuickSort(a, begin, key - 1); QuickSort(a, key + 1, end);
}
递归的返回条件:当区间不存在或区间只有一个值时,此时无需再排序。
②结果演示
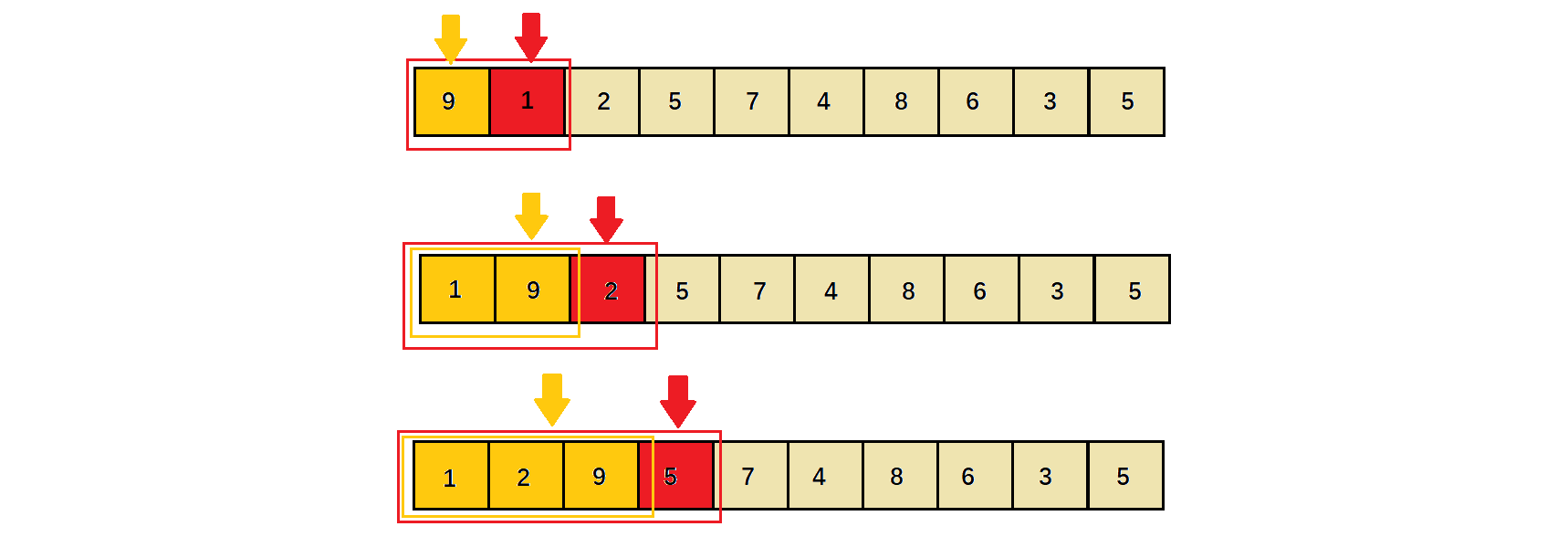
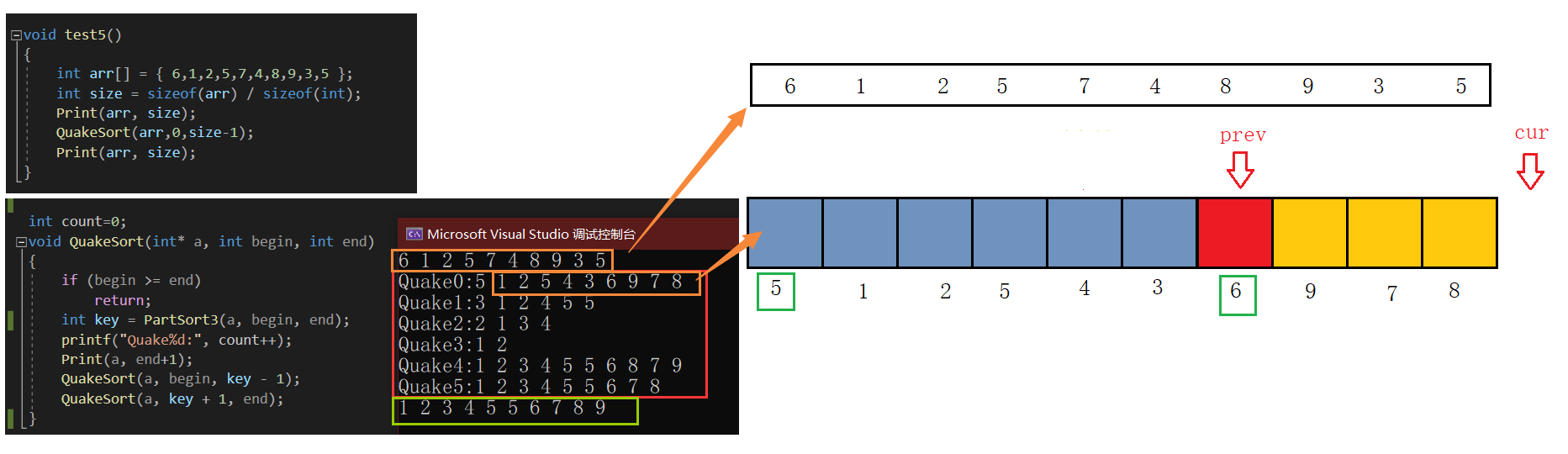
测试结果如下:
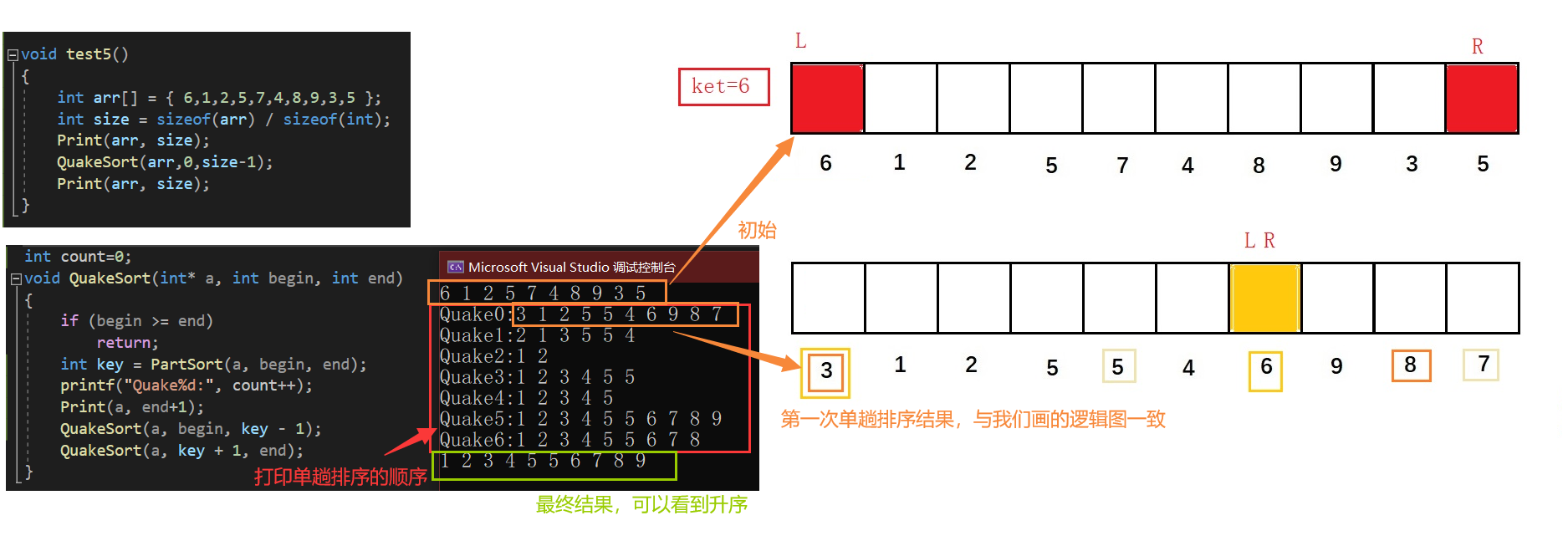
代码如下:
void test5()
{int arr[] = { 6,1,2,5,7,4,8,9,3,5 };int size = sizeof(arr) / sizeof(int);Print(arr, size);QuickSort(arr,0,size-1);Print(arr, size);
}
int count=0;
void QuickSort(int* a, int begin, int end)
{if (begin >= end)return;int key = PartSort(a, begin, end);printf("Quake%d:", count++);Print(a, end+1);QuickSort(a, begin, key - 1);QuickSort(a, key + 1, end);
}
4.2.2、挖坑法
4.2.2.1、单趟
①思路分析
1)、思路分析
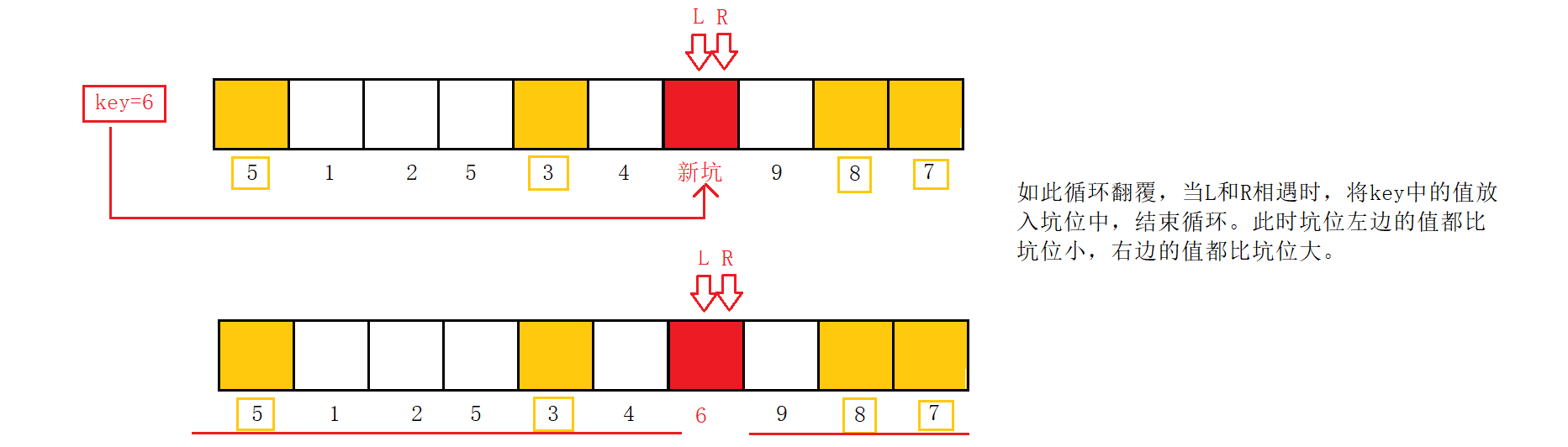
先得到第一个数据存放在临时变量key中,形成一个坑位,key=6。

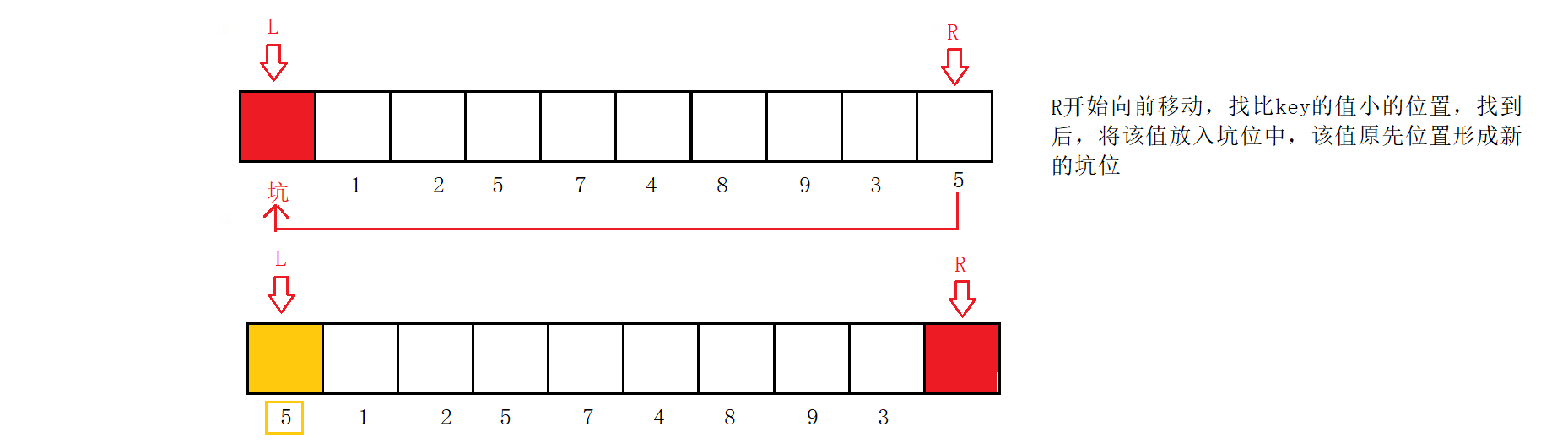
R开始向前移动,找比key的值小的位置,找到后,将该值放入坑位中,该值原先位置形成新的坑位;
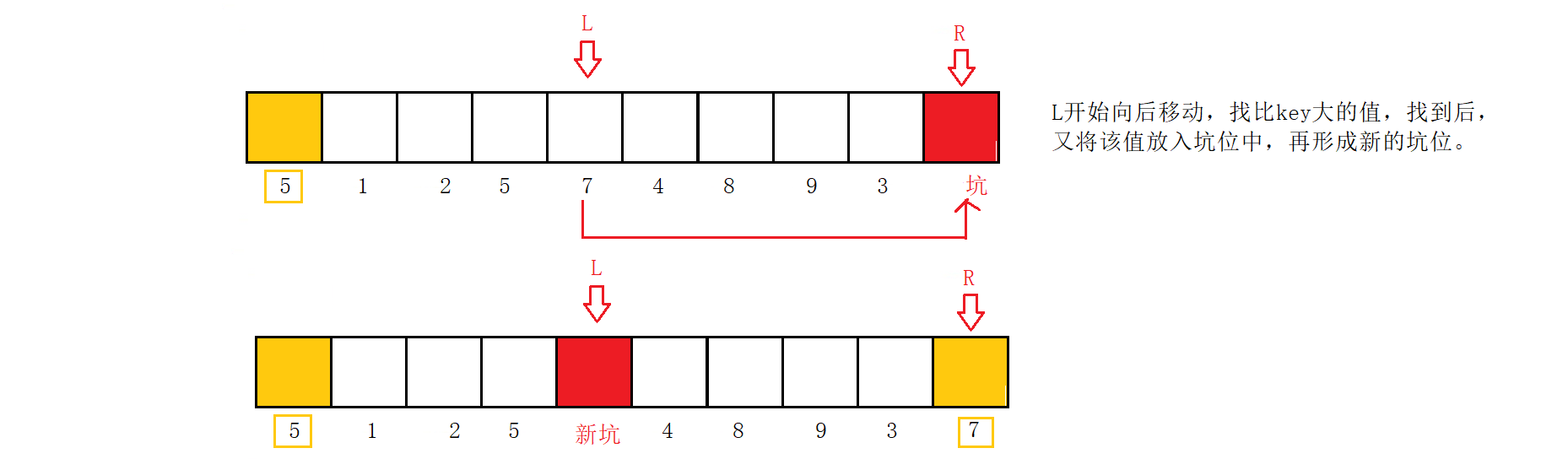
L开始向后移动,找比key大的值,找到后,又将该值放入坑位中,再形成新的坑位。
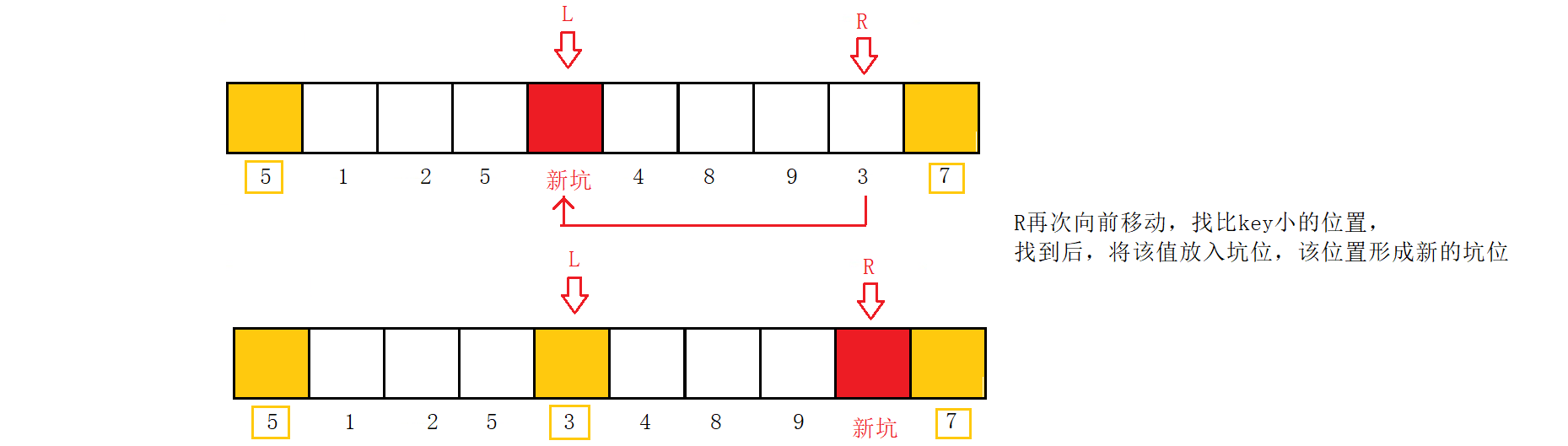
R再次向前移动,找比key小的位置,找到后,将该值放入坑位,该位置形成新的坑位;
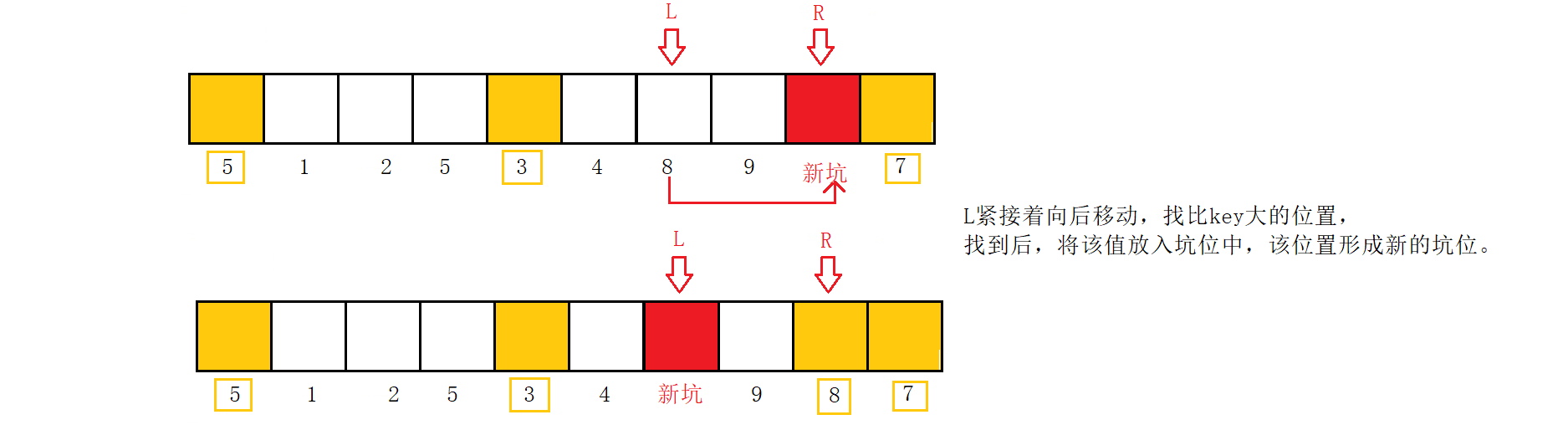
L紧接着向后移动,找比key大的位置,找到后,将该值放入坑位中,该位置形成新的坑位。
如此循环翻覆,当L和R相遇时,将key中的值放入坑位中,结束循环。此时坑位左边的值都比坑位小,右边的值都比坑位大。
此法相较于上一种方法,在于提高了理解性,不必纠结于为什么先走右边再走左边。在一轮中,L、R有一个充当了坑位,坑位本身是固定不能移动的,因此只能移动L、R中非坑位的走向。
②相关实现
2)、相关实现
int PartSort2(int* a, int begin, int end)
{int left = begin, right = end;int key = a[left], pit = left;//pit用于记录坑位下标while (left < right){if (left < right && a[right] >= key)//左有坑,排升序在右找小--right;a[pit] = a[right];//找到后将数据填入坑中pit = right;//右形成新坑if (left < right && a[left] <= key)//右为坑,升序在左找大++left;a[pit] = a[left];//找到后填入坑中pit = left;//左边形成新坑}a[pit] = key;//最后坑中填入基准数keyreturn pit;
}
4.2.2.2、总趟
事实上,这几种方法中,总趟的实现保持不变,用递归法仍旧等同于二叉树的前序遍历。只是把hoare版中单趟实现方法改为这里挖坑法中单趟实现。
只是此法相较于上一种方法,在于提高了理解性,不必纠结于为什么先走右边再走左边。在一轮中,L、R有一个充当了坑位,坑位本身是固定不能移动的,因此只能移动L、R中非坑位的走向。
void QuickSort(int* a, int begin, int end)
{if (begin >= end)return;int key = PartSort2(a, begin, end);QuickSort(a, begin, key - 1);QuickSort(a, key + 1, end);
}
相关验证如下:
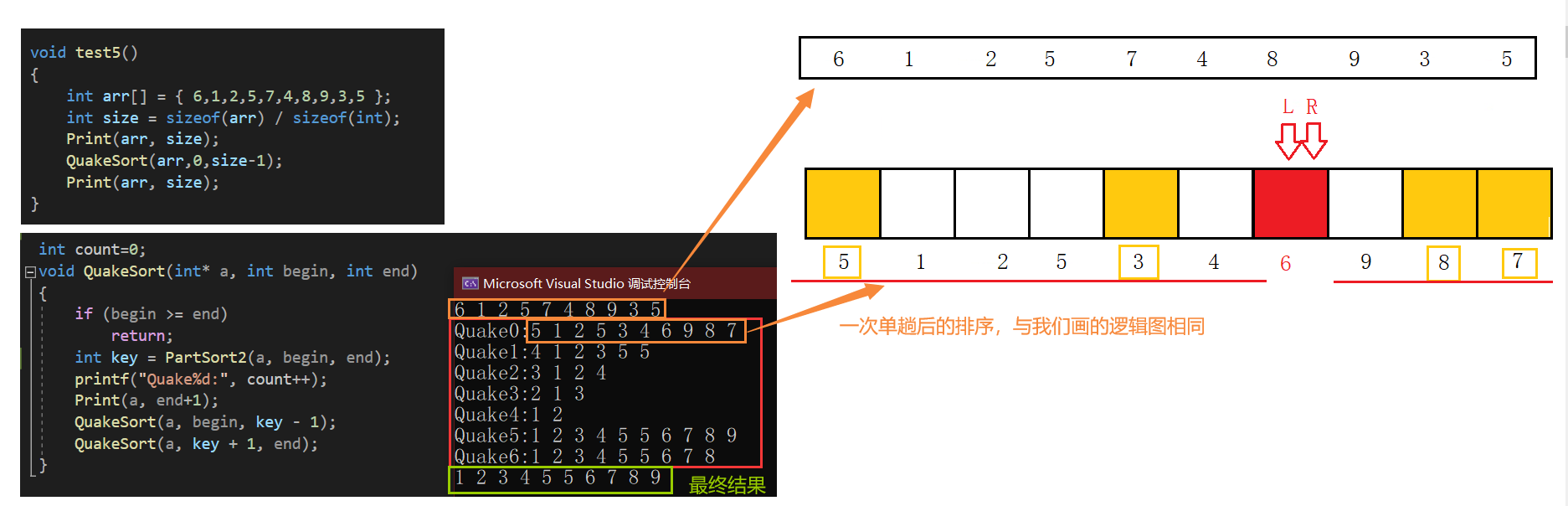
验证代码如下:
int count=0;
void QuickSort(int* a, int begin, int end)
{if (begin >= end)return;int key = PartSort2(a, begin, end);printf("Quake%d:", count++);Print(a, end+1);QuickSort(a, begin, key - 1);QuickSort(a, key + 1, end);
}
void test5()
{int arr[] = { 6,1,2,5,7,4,8,9,3,5 };int size = sizeof(arr) / sizeof(int);Print(arr, size);QuickSort(arr,0,size-1);Print(arr, size);
}
4.2.3、前后指针法
4.2.3.1、单趟
①思路分析
1)、思路分析
初始时,prev指针指向序列开头,cur指针指向prev指针的后一个位置。

然后判断cur指针指向的数据是否小于key,若小于,则prev指针后移一位,并让cur指向的数据与prev指向的数据交换,然后cur指针自增。
当cur指针指向的数据仍旧小于key时,重复上述步骤。若cur指针指向的数据大于key,则cur指针自增。
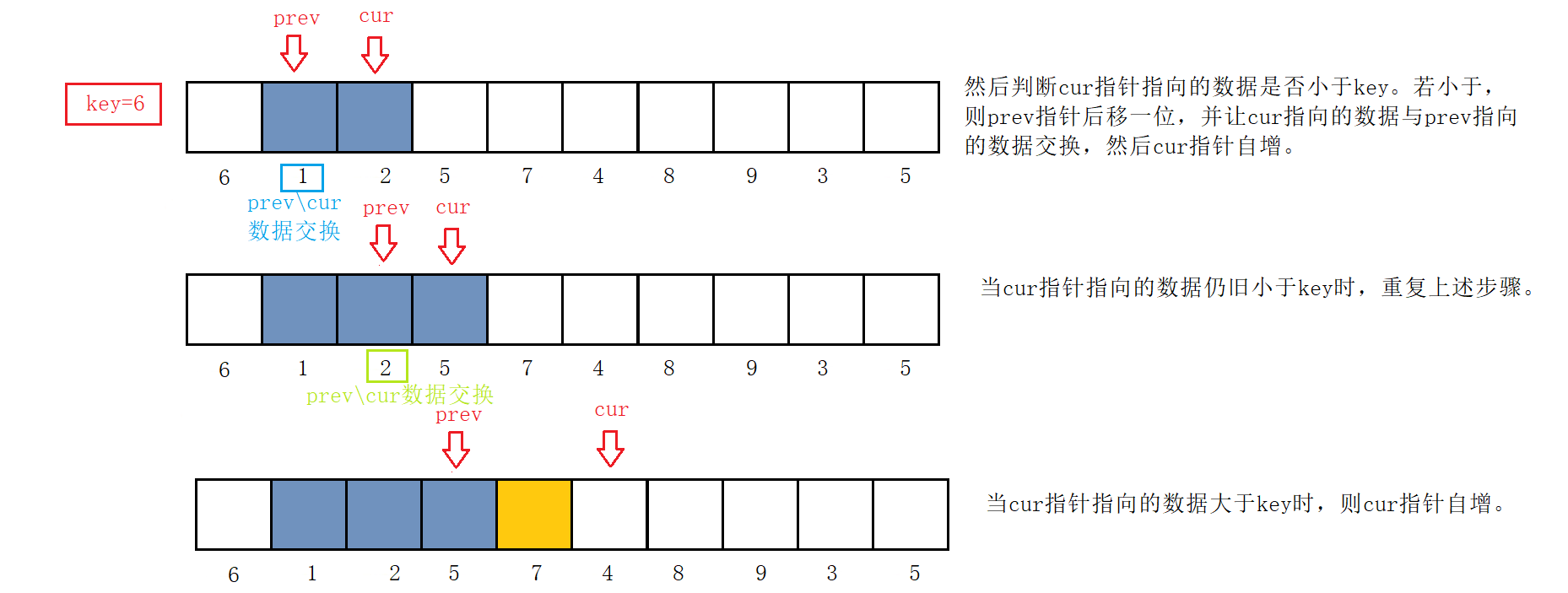
此后只需要重复上述cur指向数据与key指向数据大小判断即可。
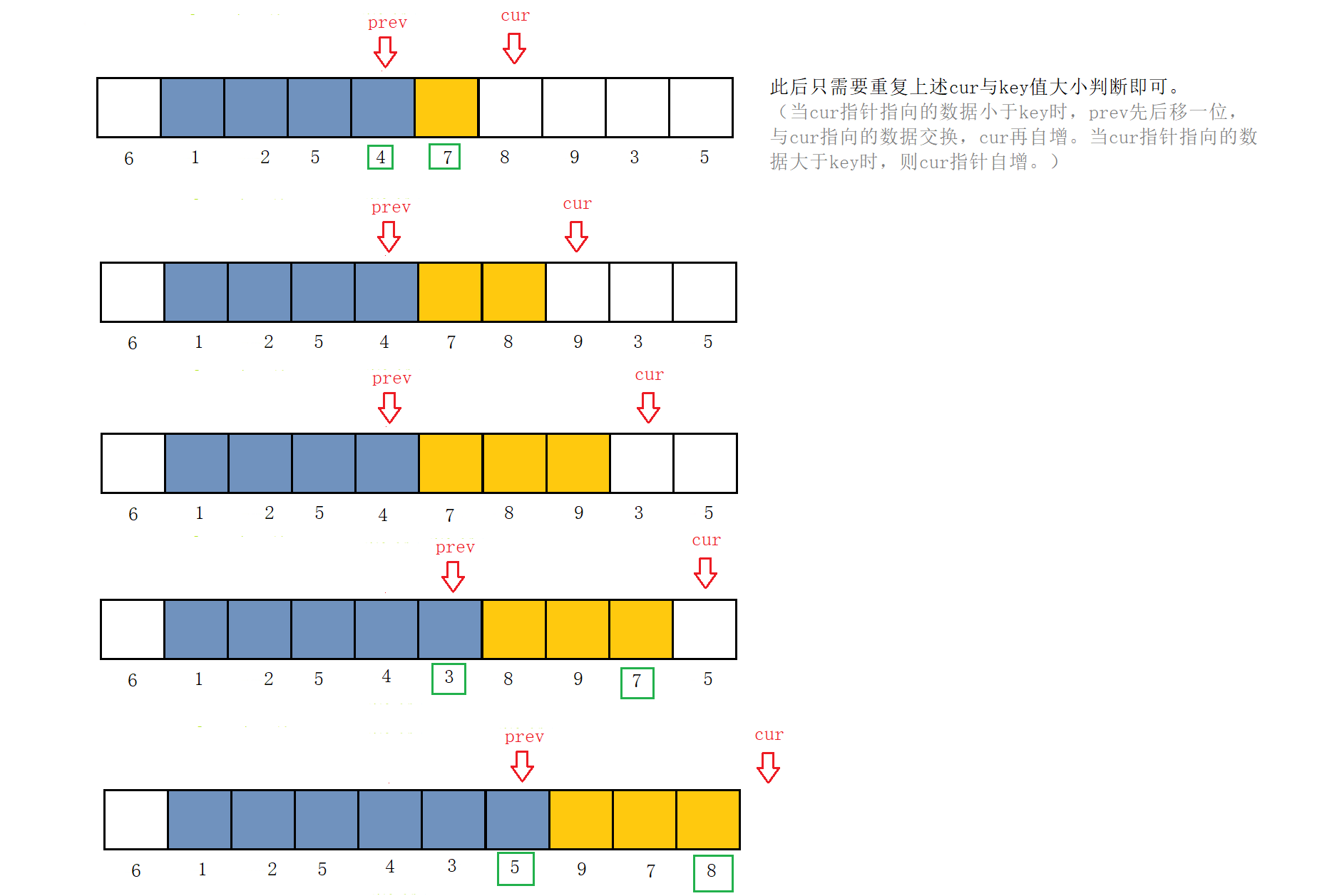
当cur指针往后走到已经越界,这时我们将prev下标指向的数据与key进行交换。结束,此时key左边的数据比key小,key右边的数据比key大。

②相关实现
2)、相关实现
int PartSort3(int* a, int begin, int end)
{int prev = begin, cur = begin + 1;int key = begin;while (cur <= end)//[begin,end],下标{if (a[cur]<a[key]){++prev;Swap(&a[prev], &a[cur]);}++cur;}Swap(&a[prev], &a[key]);//cur首次越界后,将prev下标指向的数据与key进行交换key = prev;return key;
}
4.2.3.2、总趟
和挖坑法一致,这里的三种写法,区别在于单趟的实现,总趟仍旧是采取递归方法实现。
从理解角度来讲,使用前后指针理解起来更容易(没有那么多弯弯绕绕)。
void QuickSort(int* a, int begin, int end)
{if (begin >= end)return;int key = PartSort3(a, begin, end);QuickSort(a, begin, key - 1);QuickSort(a, key + 1, end);
}
相关验证:
int count=0;
void QuickSort(int* a, int begin, int end)
{if (begin >= end)return;int key = PartSort3(a, begin, end);printf("Quake%d:", count++);Print(a, end+1);QuickSort(a, begin, key - 1);QuickSort(a, key + 1, end);
}
void test5()
{int arr[] = { 6,1,2,5,7,4,8,9,3,5 };int size = sizeof(arr) / sizeof(int);Print(arr, size);QuickSort(arr,0,size-1);Print(arr, size);
}
4.2.4、快排优化1.0:关于key值的选取
1)、问题说明
对于上述的快排方法,选择出来的基数key影响快排效率。
①key影响递归效率的原因说明:
若所选择的key接近于中位数,则效率相对较优(相当于此时接近二分,快排中递归类似于二叉树的前序遍历,其时间复杂度和深度有关,左右均衡时二叉树深度相对较小)。
②什么情况下,取端点作为key值,会造成所选数极大/极小:
我们一般取左右端点数为key值,当所给数组原先就有序或接近有序,很容易选出的key就是极小值/极大值的情况。此时快排效率相对较低:
1、当数据很多时,由于递归的深度很深,而栈空间相对而言不是那么大,容易出现栈溢出的现象。
2、此外这种最坏情况下,时间复杂度O(N)=N+N-1+N-2+……+1≈O(N^2) 。

因此,针对上述情况,我们需要对key值做出改进。
2)、解决方案
解决方法如下:
法一:随机选择key。
法二:三数取中。对数组第一个数据、下标在中间的数据、最后一个数据做比较。选择三个数的中间数作为key值,这里我们将key所在下标元素与mid下标元素交换即可。(这样做能保证后续遍历排序时,所有数据轮番遍历到,也不用做过多调整。即整体大逻辑框架不变。)
int GetMidIndex(int* a, int begin, int end)
{int mid = (begin + end) / 2;if (a[begin] > a[end]){if (a[end] > a[mid])//begin>end>midreturn end;else if (a[begin] > a[mid])//begin>mid>endreturn mid;elsereturn begin;//mid>begin>end}else//a[begin]<=a[end]{if (a[begin] > a[mid])//end>begin>midreturn begin;else if (a[mid] > a[end])return end;elsereturn mid;}
}
在单趟排序中只需要做key下标和mid下标元素位置交换即可(此处以前后指针法来举例)。
int PartSort3(int* a, int begin, int end)
{int prev = begin, cur = begin + 1;int key = begin;int mid = GetMidIndex(a, begin, end);Swap(&a[key], &a[mid]);while (cur <= end)//[begin,end],下标{if (a[cur]<a[key]){++prev;Swap(&a[prev], &a[cur]);}++cur;}Swap(&a[prev], &a[key]);//cur首次越界后,将prev下标指向的数据与key进行交换key = prev;return key;
}
相关验证如下:
#include<time.h>
void TestQuickSort()
{srand(time(0));const int N = 50000000;int* a1 = (int*)malloc(sizeof(int) * N);assert(a1);int* a2 = (int*)malloc(sizeof(int) * N);assert(a2);for (int i = 0; i < N; ++i){a1[i] = rand();a2[i] = a1[i];}int begin1 = clock();QuickSortpro(a1, 0, N - 1);int end1 = clock();int begin2 = clock();QuickSort(a2, 0, N - 1);int end2 = clock();printf("QuickSortpro:%d\n", end1 - begin1);printf("QuickSort:%d\n", end2 - begin2);free(a1);free(a2);}
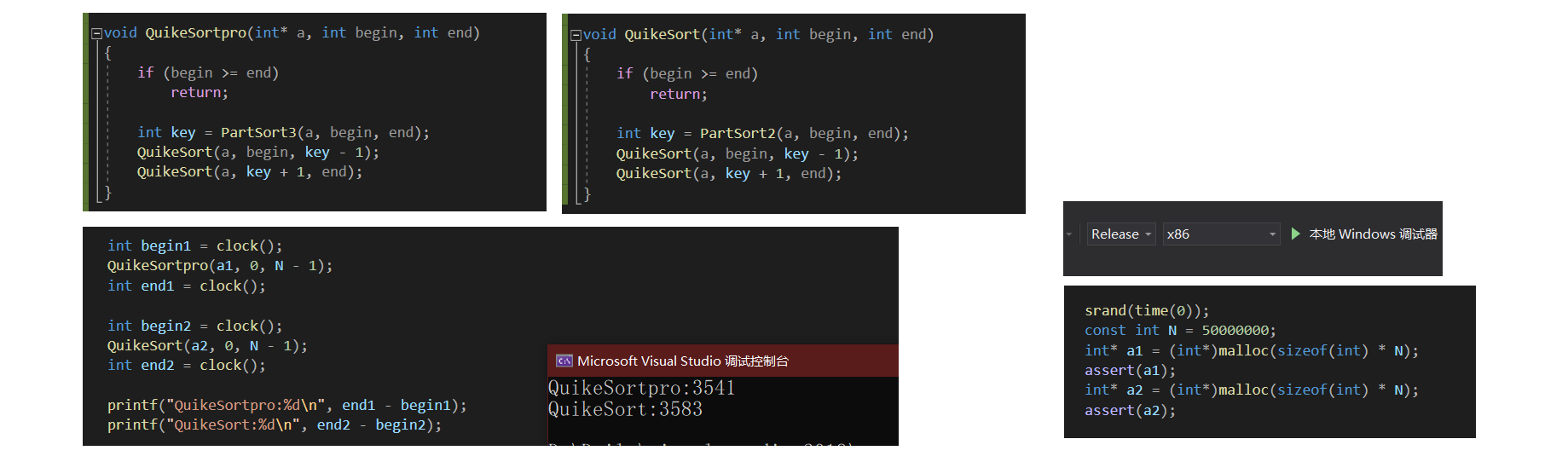
4.2.5、快排优化2.0:小区间优化
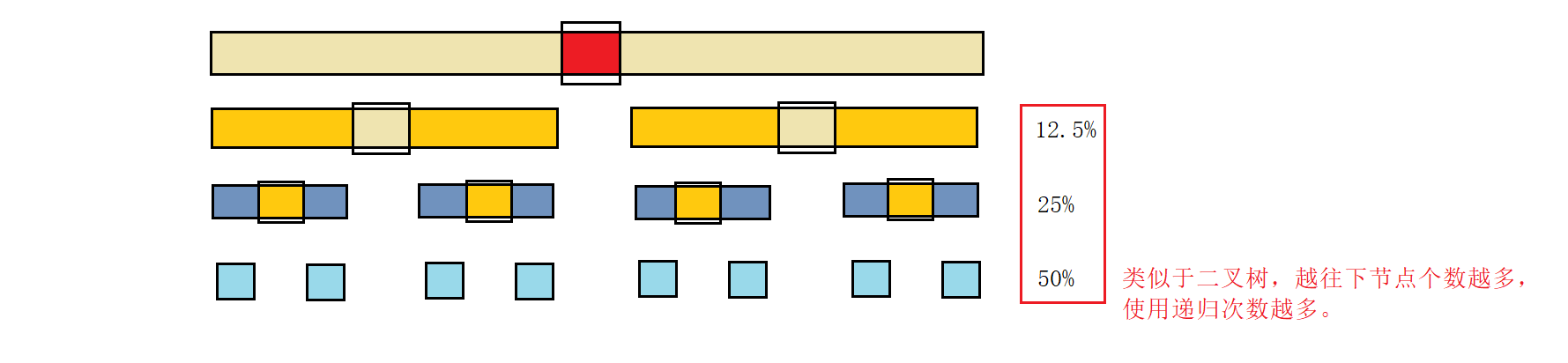
1)、问题说明
递归划分区间,当区间比较小时,就不再用递归划分去排序这个小区间,可以考虑使用其它排序对小区间做处理。比如:直接插入排序(希尔排序针对大量数据),如此可减少很多递归次数。
该调整在QuickSort总趟中。
解决方案如下:给定一个范围,当单趟排序中区间内元素数量相对少时,就使用其它排序来完成。
void QuickSortpro(int* a, int begin, int end)
{if (begin >= end)return;if (end - begin > 10){int key = PartSort3(a, begin, end);QuickSort(a, begin, key - 1);QuickSort(a, key + 1, end);}elseInsertSort(a+begin, end - begin + 1);
}
end - begin > 10给定一个适合的区间值,当区间大于该值时仍旧使用递归,否则就使用其它排序方法。
InsertSort(a+begin, end - begin + 1);注意这里的参数传递。快排中使用直接插入排序,第一参数为对应小区间首元素地址(不能直接传递a),第二参数为小区间数据个数(begin、end为下标)。
4.2.6、快排:针对总趟的非递归写法
1)、问题说明
为什么要学习非递归方法: 极端场景下,如果深度太深,会出现栈溢出的现象。故而此处要面对的一个问题是:如何把递归改为非递归?
改法一: 将递归直接该为循环,例如斐波那契额数列、归并排序
改法二: 用数据结构栈或队列模拟递归过程
这里快排的非递归法就要使用上述法二。这里借助的是栈。
关键点:如何使用栈模拟递归过程?
快排中需要用到递归的是总趟,故而这里单趟写法照旧不变,使用上述三种写法即可。总趟中,我们每次递归改变的是单趟排序的区间,故而使用栈时,关键点在于如何在栈中存储我们需要的区间位置,以便取出用于单趟排序?
结合栈后进先出的性质。我们先把左右区间[begin,end]入栈,先入end,再入begin,这样top取栈顶元素时,才能按顺序取到begin、end两值。
根据取出的区间,进行单趟排序。此时我们能得到keyi值,将区间分为[left,key-1] 、key、[key+1,right]三部分,再重复上述入栈操作,对左右两区间分别入栈、取出排序,如此循环直到所排区间为单元素即可。
void QuickSortNonR(int* a, int begin, int end)
{ST stack;StackInit(&stack);StackPush(&stack, begin);StackPush(&stack, end);while (!StackEmpty(&stack))//栈不为空时循环继续,说明还有区间没有排完{int left = StackTop(&stack);//取区间左端StackPop(&stack);int right = StackTop(&stack);//取区间右端StackPop(&stack);int keyi = PartSort3(a, left, right);//单趟排序得到key值//[left,key-1] key [key+1,right]if (right > keyi + 1)//key+1<right时,表明此时右区间中值大于一个{StackPush(&stack, right);StackPush(&stack, keyi + 1);}if (left < keyi - 1)//left < key - 1时,表明此时左区间中值大于一个{StackPush(&stack, keyi - 1);StackPush(&stack, left);}}StackDestroy(&stack);
}
此处若不使用栈来模拟递归(处理过程类似于二叉树的前序遍历),也可以使用队列完成(处理过程类似于二叉树的层序遍历),只不过队列的特性是先进先出,入队时需要注意区间选择问题。
5、归并排序
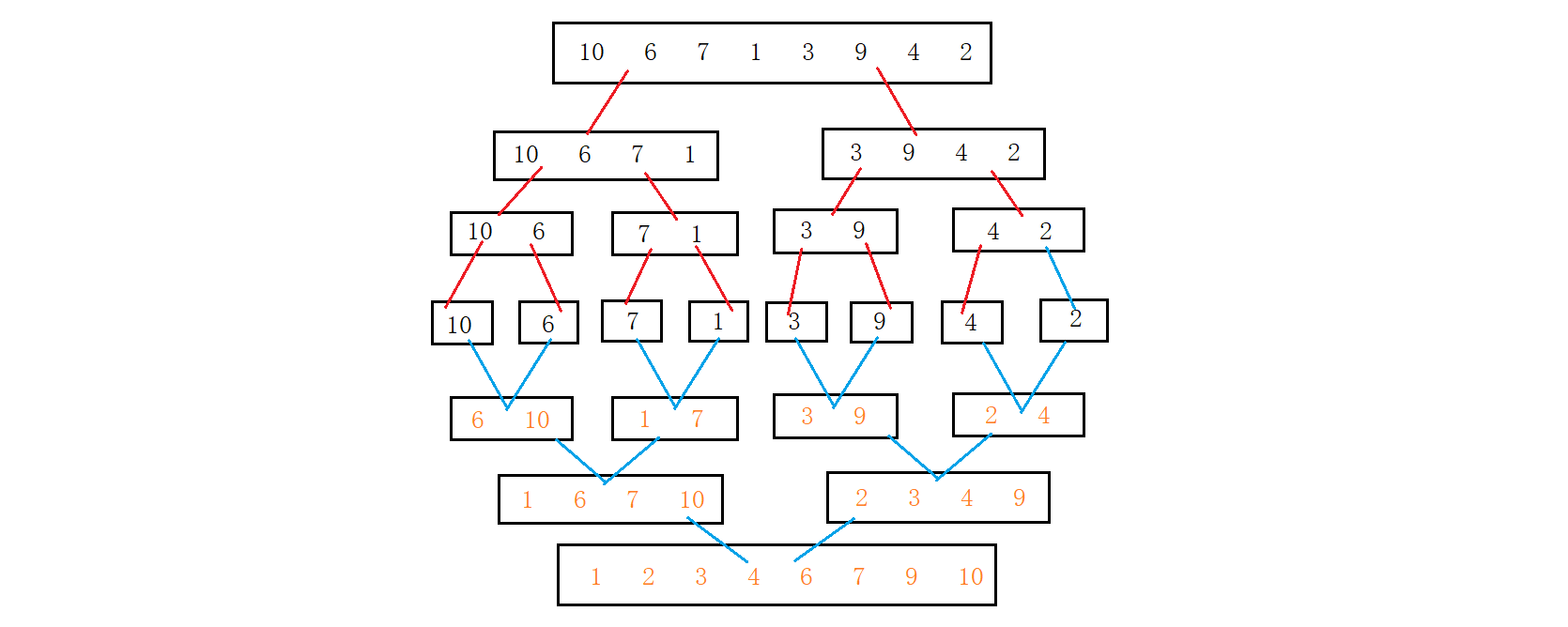
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法的一个非常典型的应用。其大致思想为:将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
示意图如下:
5.1、递归版
1)、思路说明
按照上述描述,给定一个数组区间[begin,end],设中间值为mid,要让其有序,则需要先让其左右子区间有序即[begin,mid]、[mid+1,end],只有在左右子区间有序的情况下,我们才能对当前整个区间进行归并排序。这个步骤就类似于二叉树的后续遍历。
需要注意的是,链式二叉树中,由于其每个节点单独开辟,并归时只需要改变指针指向即可。而这里数组是一段连续的物理空间,若直接在原数组改动会导致数据覆盖问题,因此此处我们借助了额外的数组。
2)、相关实现
void _MergeSort(int* a, int begin, int end,int*tmp)
{if (begin >= end)return;int mid = (begin + end) / 2;//step1:让左右区间有序,[begin,mid]、[mid+1,end]_MergeSort(a, begin, mid, tmp);_MergeSort(a, mid + 1, end, tmp);//step2:并归,类似于两个数组比较取二者max/min排序int begin1 = begin, end1 = mid;int begin2 = mid + 1, end2 = end;int cur = begin1;//此处不能直接使cur赋值为0,因为子序列是从[begin,end]开始,begin在不同的子序列中下标不同while (begin1 <= end1 && begin2 <= end2)//两区间均有值{if (a[begin1] < a[begin2])//以升序为例tmp[cur++] = a[begin1++];elsetmp[cur++] = a[begin2++];}while (begin1 <= end1)//处理剩余区间tmp[cur++] = a[begin1++];while (begin2 <= end2)tmp[cur++] = a[begin2++];//step3:将tmp中排序好的数据放回原数组相应位置memcpy(a + begin, tmp + begin, (end - begin + 1)*sizeof(int));
}void MergeSort(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);assert(tmp);_MergeSort(a, 0, n - 1, tmp);//开区间还是闭区间看自己控制free(tmp);
}
注意细节:
1、递归返回条件:begin >= end
2、两数组比较归并时,tmp遍历下标:int cur = begin1;
3、如何将本回合归并结果拷贝回原数组中:memcpy(a + begin, tmp + begin, (end - begin + 1)*sizeof(int));。注意这里我们整体排序的是[begin、end]区间,只是排序它时是将其分为子区间排序。
5.2、非递归版
1)、思路说明
Q:前面我们有介绍递归改非递归通常有两种方法,这里归并排序的非递归写法是否像快排一样需要借助栈或队列?
A:不需要。归并非递归法不适合用借助栈,在上面的快排中,由于前序遍历,使用栈或队列不影响排序。而此处的并归排序中,属于后续遍历,需要先处理其左右子区间,得到有序数组才能处理本身。考虑到上述因素,这里我们直接使用循环达到递归效果。
逻辑图如下:
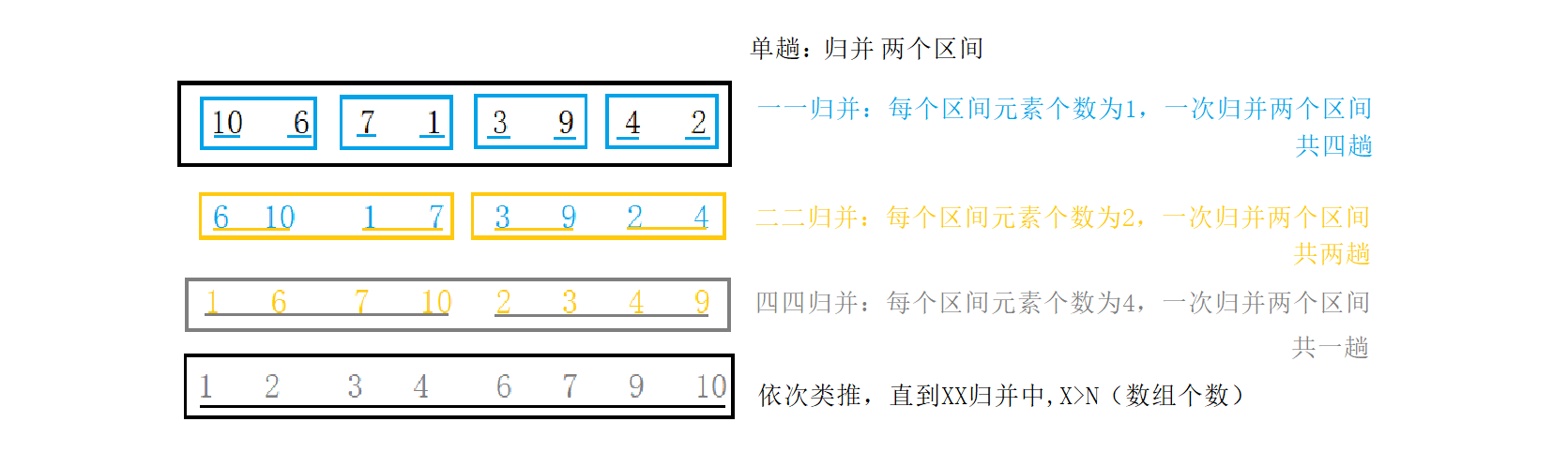
5.2.1、版本1.0
5.2.1.1、写法
这里我们以gap作为XX归并。则需要归并的两区间为[i,i+gap-1]、[i+gap,i+gap*2-1]。i用于确定每次需要比较的两区间中,首个区间左下标,其余区间下标依据i和gap来确定。
根据上述,对于单趟(归并:两区间比较排序)的排序逻辑仍旧保持不变,此处只是不再使用递归控制总趟(这里我们使用了循环)。
void MergeSortNonR(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);assert(tmp);int gap = 1;while (gap < n){for (int i = 0; i < n; i += 2 * gap)//2*gap:一个gap代表一组间距,归并一次需要两组,故下次从第三组开始{//区间:[i,i+gap-1]、[i+gap,i+gap*2-1]int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + gap * 2 - 1;int cur = begin1;//此处不能直接使cur赋值为0while (begin1 <= end1 && begin2 <= end2)//两区间均有值{if (a[begin1] < a[begin2])//以升序为例tmp[cur++] = a[begin1++];elsetmp[cur++] = a[begin2++];}while (begin1 <= end1)//处理剩余区间tmp[cur++] = a[begin1++];while (begin2 <= end2)tmp[cur++] = a[begin2++];}memcpy(a, tmp, sizeof(int) * n);gap *= 2;}free(tmp);
}
可以看到对于下述举例2的倍数,我们可以很好的完成排序:
5.2.1.2、问题
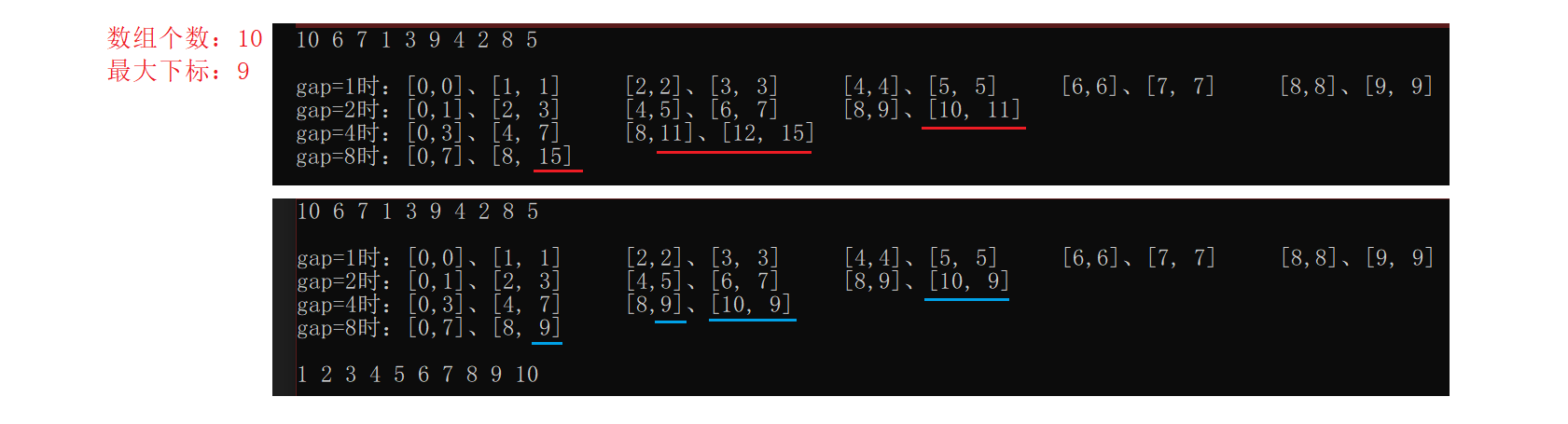
但是对于非2的倍数的数组,存在越界等情况:

这里我们再打印演示看看:

printf("\ngap=%d时:", gap);
printf("[%d,%d]、[%d, %d] ", begin1, end1, begin2, end2);
5.2.2、版本2.0
考虑到上述问题,我们需要对会发生越界的下标进行修正。以下给出两种写法,总体修正方法一致,这里的法一、法二区别在于何时memcpy。
5.2.2.1、写法一
修正部分代码如下:
//step2:修正区间if (end1 >= n){end1 = n - 1;begin2 = n;end2 = n - 1;}else if (begin2 >= n){begin2 = n;end2 = n - 1;}else if (end2 >= n){end2 = n - 1;}
相关验证如下:

整体如下:
void MergeSortNonR(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);assert(tmp);int gap = 1;while (gap < n){for (int i = 0; i < n; i += 2 * gap)//2*gap:一个gap代表一组间距,归并一次需要两组,故下次从第三组开始{//step1:分区间:[i,i+gap-1]、[i+gap,i+gap*2-1]int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + gap * 2 - 1;int cur = begin1;//此处不能直接使cur赋值为0//step2:修正区间if (end1 >= n){end1 = n - 1;begin2 = n;end2 = n - 1;}else if (begin2 >= n){begin2 = n;end2 = n - 1;}else if (end2 >= n){end2 = n - 1;}//step3:归并,两区间元素比较排序while (begin1 <= end1 && begin2 <= end2)//两区间均有值{if (a[begin1] < a[begin2])//以升序为例tmp[cur++] = a[begin1++];elsetmp[cur++] = a[begin2++];}while (begin1 <= end1)//处理剩余区间tmp[cur++] = a[begin1++];while (begin2 <= end2)tmp[cur++] = a[begin2++];}memcpy(a, tmp, sizeof(int) * n);//同gap组一次性归并gap *= 2;}printf("\n");free(tmp);
}
注意事项:
1、if、else if:这几种修正关系为互斥情况。注意需要把正常情况也考虑进去。
2、对于区间[begin1,end1]、[begin2,end2],若end1、begin2、end2越界,能否将区间修正为[begin1,begin1]、[begin1,begin1]?例如:[8,9]、[10,11],将其修正为[8,8]、[8,8]。
回答:不能。这里memcpy(a, tmp, sizeof(int) * n);我们是在每次XX归并后将整个数组拷贝回去,若依照上述方法修正,则会多出一个数据。故此处需要将其修正为不存在区间。
3、同理,上述情况能否不修正[begin2,end2]值,直接返回?
else if (begin2 >= n || end2 >=n){break;}
回答:在这种单趟排完后才拷贝回原数组的情况下,不能这样做,原因:会将tmp中随机数拷贝回去。

5.2.2.2、写法二
法一中我们是将单趟排序完成后,将tmp中数据拷贝回原数组,这里也可以每次排完序都进行拷贝:
void MergeSortNonR_2(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);assert(tmp);int gap = 1;while (gap < n){printf("\ngap=%d时:", gap);for (int i = 0; i < n; i += 2 * gap)//2*gap:一个gap代表一组间距,归并一次需要两组,故下次从第三组开始{//step1:分区间:[i,i+gap-1]、[i+gap,i+gap*2-1]int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + gap * 2 - 1;int cur = begin1;//此处不能直接使cur赋值为0//step2:修正区间if (end1 >= n || begin2 >= n){break;}else if (end2 >= n)//需要修正边界{end2 = n - 1;}printf("[%d,%d]、[%d, %d] ", begin1, end1, begin2, end2);int space = end2 - begin1 + 1;//step3:归并,两区间元素比较排序while (begin1 <= end1 && begin2 <= end2)//两区间均有值{if (a[begin1] < a[begin2])//以升序为例tmp[cur++] = a[begin1++];elsetmp[cur++] = a[begin2++];}while (begin1 <= end1)//处理剩余区间tmp[cur++] = a[begin1++];while (begin2 <= end2)tmp[cur++] = a[begin2++];memcpy(a+i, tmp+i, sizeof(int) * space);//单组归并}gap *= 2;}printf("\n");free(tmp);
}
6、计数排序
基本思路:
1. 统计相同元素出现次数
2. 根据统计的结果将序列回收到原来的序列中
局限性:
1、如果是浮点数、字符串,就不能使用这种方法。
2、如果数据范围很大,空间复杂度很高,相对不适合。这个排序不适用的是数据之间跨度比较大的情况。其相对适合范围集中,重复数较多的排序。
注意事项:
1、若数值很大:例如,数组数据为1000、1001、1002等,如果使用绝对映射,则数组开辟需要到一千个空间以上。故可使用相对映射法。
2、若是负数:仍旧可以用元素-最小值的方法得到数值。
//时间复杂度O(max(range,N))
//空间复杂度O(range)
void CountSort(int* a, int n)
{//计算数组最大最小值int min = a[0], max = a[0];for (int i = 1; i < n; i++){if (a[i] < min)min = a[i];if (a[i] > max)max = a[i];}//统计次数的数组int range = max - min + 1;//需要开辟一个能装下最大数与最小数元素差的数组,[min,max]之间的数据在数组中按顺序各占一个元素位置int* count = (int*)malloc(sizeof(int) * range);if (count == NULL){printf("malloc:fail\n");exit(-1);}memset(count, 0, sizeof(int) * range);//先将该统计数组内元素初始化为0//统计次数for (int i = 0; i < n; i++)//将原数组元素中出现的值做统计{count[a[i] - min]++;//-min是相对映射,使原数组值在统计数组中从0开始,也能解决负数问题}//回写排序int j = 0;for (int i = 0; i < range; i++){while (count[i]--)//统计数组中该值出现几次,在原数组中映射元素就写入几次{a[j++] = i + min;//+min为映射回去}}
}
相关文章:

【ONE·Data || 常见排序说明】
总言 数据结构基础:排序相关内容。 文章目录总言1、基本介绍2、插入排序2.1、直接插入排序:InsertSort2.1.1、单趟2.1.2、总趟2.2、希尔排序(缩小增量排序):ShellSort2.2.1、预排序1.0:单组分别排序2.…...

本节作业之跟随鼠标的天使、模拟京东按键输入内容、模拟京东快递单号查询
本节作业之跟随鼠标的天使、模拟京东按键输入内容、模拟京东快递单号查询1 跟随鼠标的天使2 模拟京东按键输入内容3 模拟京东快递单号查询1 跟随鼠标的天使 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><met…...

ChatGPT 被大面积封号,到底发生什么了?
意大利数据保护机表示 OpenAI 公司不但非法收集大量意大利用户个人数据,没有设立检查 ChatGPT 用户年龄的机制。 ChatGPT 似乎正在遭遇一场滑铁卢。 3月31日, 大量用户在社交平台吐槽,自己花钱开通的 ChatGPT 账户已经无法登录,更…...

教你精通JavaSE语法之第十一章、认识异常
一、异常的概念与体系结构 1.1异常的概念 在Java中,将程序执行过程中发生的不正常行为称为异常。比如之前写代码时经常遇到的: 1.算术异常 System.out.println(10 / 0); // 执行结果 Exception in thread "main" java.lang.ArithmeticExcep…...

display、visibility、opacity隐藏元素的区别
display、visibility、opacity隐藏元素的区别 display: none 事件监听:无法进行DOM事件监听。 元素从网页中消失,并且不占据位置再次从网页中出现会引起重排 进而引起重绘继承:不会被子元素继承,因为子元素也不被渲染。 visib…...

Linux Shell 实现一键部署tomcat10+java13
tomcat 前言 Tomcat 服务器是一个免费的开放源代码的Web 应用服务器,属于轻量级应用服务器,在中小型系统和并发访问用户不是很多的场合下被普遍使用,是开发和调试JSP 程序的首选。对于一个初学者来说,可以这样认为,当…...

软硬皆施,WMS仓库管理系统+PDA,实现效率狂飙
人工经验Excel表格,是传统第三方仓储企业常用的管理模式。在这种管理模式下,对仓库员工的Excel操作能力、业务经验和工作素养要求极高。一旦员工的经验能力不足,就会导致仓库业务运行不顺畅,效率低下,而员工也会因长时…...
DJ3-2 传输层(第二节课)
目录 一、如何实现可靠数据传输 1. 需要解决地问题 2. 使用的描述方法 二、rdt1.0:完全可靠信道上的可靠数据传输 1. 前提条件 2. 有限状态机 FSM 三、rdt2.0:仅具有 bit 错误的信道上的可靠数据传输 1. 前提条件 2. 有限状态机 FSM 3. 停等协…...
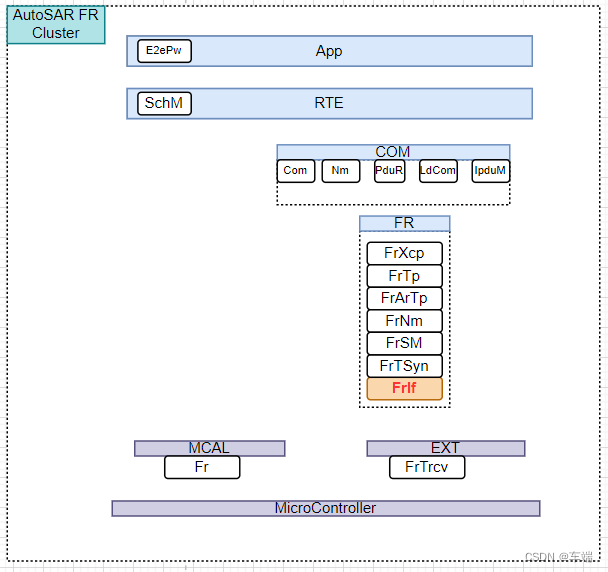
FrIf-FrIf功能模块概述和与底层驱动的交互
总目录链接==>> AutoSAR入门和实战系列总目录 总目录链接==>> AutoSAR BSW高阶配置系列总目录 文章目录 1 FlexRay 接口模块概述2 与FlexRay底层驱动的交互1 FlexRay 接口模块概述 FlexRay 接口模块通过 FlexRay 驱动程序模块间接与 FlexRay 控制器通信。 它…...
)
【LeetCode】前 K 个高频元素(堆)
目录 1.题目要求: 给你一个整数数组 nums 和一个整数 k ,请你返回其中出现频率前 k 高的元素。你可以按 任意顺序 返回答案。 2.解题思路: 代码展示: 1.题目要求: 给你一个整数数组 nums 和一个整数 k ࿰…...
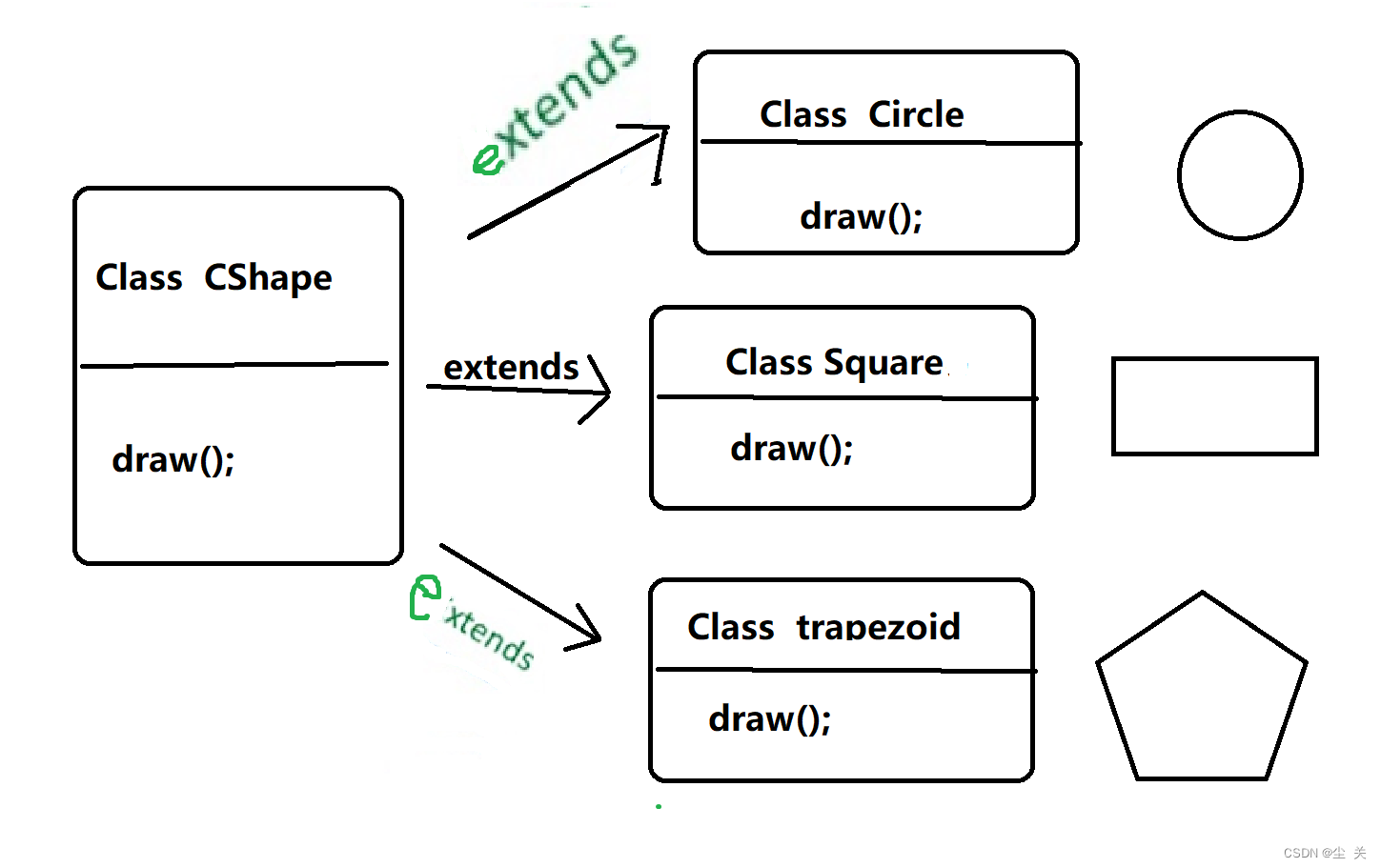
Java ---多态
(一)定义 官方:多态是同一个行为具有多个不同表现形式或形态的能力。多态就是同一个接口,使用不同的实例而执行不同操作。 生活中的多态,如图所示: 多态性是对象多种表现形式的体现。 现实中,…...

13个程序员常用开发工具用途推荐整理
作为一名刚入门的程序员,选择合适的开发工具可以提高工作效率,加快学习进度。在本文中,我将向您推荐10个常用的开发工具,并通过简单的例子和代码来介绍它们的主要用途。 1. Visual Studio Code Visual Studio Code(V…...
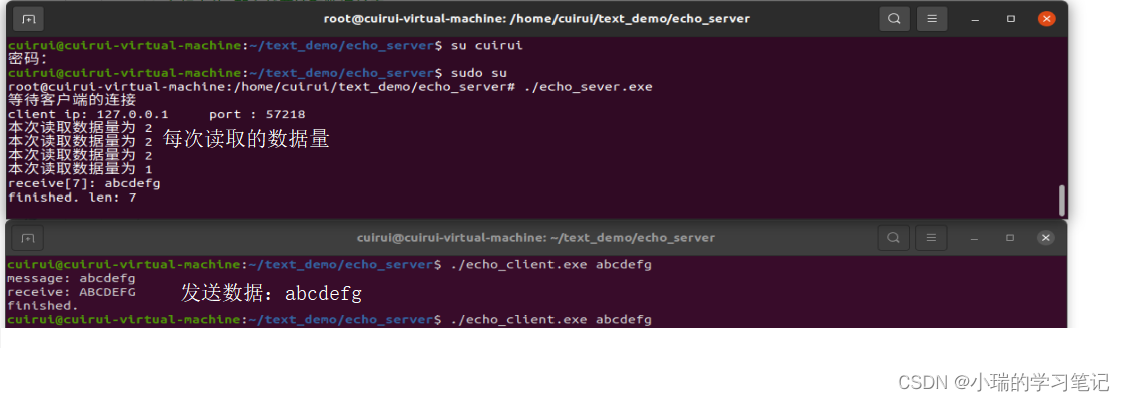
TCP分包和粘包
文章目录TCP分包和粘包TCP分包TCP 粘包分包和粘包解决方案:TCP分包和粘包 TCP分包 场景:发送方发送字符串”helloworld”,接收方却分别接收到了两个数据包:字符串”hello”和”world”发送端发送了数量较多的数据,接…...

手撕深度学习中的优化器
深度学习中的优化算法采用的原理是梯度下降法,选取适当的初值params,不断迭代,进行目标函数的极小化,直到收敛。由于负梯度方向时使函数值下降最快的方向,在迭代的每一步,以负梯度方向更新params的值&#…...

英文打字小游戏
目录 1 实验目的 2 实验报告内容 3 实验题目 4 实验环境 5 实验分析和设计思路 6 流程分析和类图结构 编辑 7. 实验结果与测试分析 8. 总结 这周没有更新任何的文章,感到十分的抱歉。因为我们老师让我们做一个英文打字的小游戏,并要求撰写实验…...

PCB生产工艺流程三:生产PCB的内层线路有哪7步
PCB生产工艺流程三:生产PCB的内层线路有哪7步 在我们的PCB生产工艺流程的第一步就是内层线路,那么它的流程又有哪些步骤呢?接下来我们就以内层线路的流程为主题,进行详细的分析。 由半固化片和铜箔压合而成,用于…...

算法竞赛进阶指南0x61 最短路
对于一张有向图,我们一般有邻接矩阵和邻接表两种存储方式。对于无向图,可以把无向边看作两条方向相反的有向边,从而采用与有向图一样的存储方式。 $$ 邻接矩阵的空间复杂度为 O(n^2),因此我们一般不采用这种方式 $$ 我们用数组模…...

[学习篇] Autoreleasepool
参考文章: https://www.jianshu.com/p/ec2c854b2efd https://suhou.github.io/2018/01/21/%E5%B8%A6%E7%9D%80%E9%97%AE%E9%A2%98%E7%9C%8B%E6%BA%90%E7%A0%81----%E5%AD%90%E7%BA%BF%E7%A8%8BAutoRelease%E5%AF%B9%E8%B1%A1%E4%BD%95%E6%97%B6%E9%87%8A%E6%94%BE/ …...

晶体基本知识
文章目录晶体基本知识基本概念晶胞<晶格<晶粒<晶体晶胞原子坐标(原子分数坐标)六方晶系与四轴定向七大晶系和十四种点阵结构学习资料吉林大学某实验室教程---知乎系列晶体与压敏器件晶体基本知识 基本概念 晶胞<晶格<…...

免费CRM如何进行选择?
如今CRM领域成为炙手可热的赛道,很多CRM系统厂商甚至打出完全免费的口号,是否真的存在完全免费的crm系统?很多企业在免费使用过程中会出现被迫终止的问题,需要花费高价钱才能继续使用,那么,免费crm系统哪个…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...
