算法竞赛进阶指南0x61 最短路
对于一张有向图,我们一般有邻接矩阵和邻接表两种存储方式。对于无向图,可以把无向边看作两条方向相反的有向边,从而采用与有向图一样的存储方式。
$$ 邻接矩阵的空间复杂度为 O(n^2),因此我们一般不采用这种方式 $$
我们用数组模拟链表:长度为n的表头数组head记录了从每个节点出发的第一条边在 ver 和 edge 数组中的存储位置,长度为 m 的边集数组 ver 和 edge 记录了每条边的终点和边权。长度为 m 的数组 next 模拟了链表指针,表示从相同节点出发的下一条边在 ver 和 edge数组中的存储位置。
$$ 邻接表的空间复杂度为 O(n + m) $$
void add(int x, int y, int z) {ver[++tot] = y, edge[tot] = z, Next[tot] = head[x], head[x] = tot;
}//访问从 x 出发的所有边
for (int i = head[x]; i; i = Next[i]) {int y = ver[i], z = edge[i];//找到了一条有向边(x, y),权值为 z
}单源最短路径
单源最短路径问题(Single Source Shortest Psth,SSSP问题) 是说,给定一张有向图 G = (V,E),V是点集,E是边集,|V| = n,|E| = m,节点以 [1,n] 之间的连续整数编号,(x,y,z) 描述一条从 x 出发,到达 y,长度为 z 的有向边。设 1 号点为起点,求长度为 n 的数组 dist,其中dist[i],表示从起点 1 到 节点 i 的最短路径的长度。
Dijkstra算法
$$ Dijkstra算法的流程如下: $$
$$ 1.初始化 dist[1] = 0,其余节点的 dist 值为正无穷大 $$
$$ 2.找出一个未被标记的、dist[x] 最小的节点 x,然后标记节点 x $$
$$ 3.扫描节点 x 的所有出边 (x,y,z),若 dist[y] > dist[x] + z,则使用 dist[x] + z 更新 dist[y] $$
$$ 4.重复上述 2 ~ 3 两个步骤,直到所有节点都被标记 $$
Dijkstra 算法基于贪心思想,它只适用于所有边的长度都是非负数的图。当边长都是非负数时,全局最小值不可能再被其他节点更新,故在第一步中选出的节点 x 必然满足:dist[x] 已经是起点到 x 的最短路径。我们不断选择全局最小值进行标记和扩展,最终可得到起点 1 到每个节点的最短路径的长度。
const int N = 1e3 + 10;
int a[N][N], d[N], n, m, s;
bool v[N];
void dijkstra(int s) {std::memset(d, 0x3f, sizeof d);d[s] = 0;for (int i = 1; i < n; i++) {//重复进行 n - 1次int x = 0;//找到未标记节点中 dist 最小的for (int j = 1; j <= n; j++) {if (!v[i] && (x == 0 || d[j] < d[x])) {x = j;}}v[x] = 1;//用全局最小值点 x 更新其他节点for (int y = 1; y <= n; y++) {d[y] = std::min(d[y], d[x] + a[x][y]);}}
}int main() {std::cin >> n >> m >> s;//构建邻接矩阵std::memset(a, 0x3f, sizeof a);for (int i = 1; i <= n; i++) {a[i][i] = 0;}for (int i = 1; i <= m; i++) {int u, v, w;std::cin >> u >> v >> w;a[u][v] = std::min(a[u][v], w);}//求单源最短路径dijkstra(s);for (int i = 1; i <= n; i++) {std::cout << d[i] << " \n"[i == n];}return 0;
}$$ 上面程序的时间复杂度为O(n^2)$$
$$ 主要瓶颈在于第一步的寻找全局最小值的过程 $$
$$ 可以用二叉堆(C++ STL priority_queue) 对 dist 数组进行维护 $$
$$ 用 O(logn) 的时间获取最小值并从堆中删除 $$
$$ 用O(logn) 的时间执行一条边的扩展和更新 $$
$$ 最终可在 O((m + n)logn) 的时间内实现 Dijkstra 算法 $$
const int N = 1e5 + 10, M = 1e6 + 10;
int head[N], ver[M], edge[M], next[M], d[N];
bool v[N];
int n, m, s, tot;
std::priority_queue<std::pair<int, int> > q;void add(int u, int v, int w) {ver[++tot] = v, edge[tot] = w, next[tot] = head[u], head[u] = tot;
}void dijkstra(int s) {std::memset(d, 0x3f, sizeof d);d[s] = 0;q.push(std::make_pair(0, s));while (q.size()) {//取出栈顶int x = q.top().second;q.pop();if (v[x]) continue;v[x] = true;//扫描所有出边for (int i = head[x]; i; i = next[i]) {int y = ver[i], z = edge[i];if (d[y] > d[x] + z) {//更新,把新的二元组插入堆d[y] = d[x] + z;q.push(std::make_pair(-d[y], y));}}}
}int main() {std::cin >> n >> m >> s;//构建邻接表for (int i = 1; i <= m; i++) {int u, v, w;add(u, v, w);}dijkstra(s);for (int i = 1; i <= n; i++) {std::cout << d[i] << " \n"[i == n];}return 0;
}Bellman - Ford 算法和 SPFA 算法
$$ 给定一张有向图,若对于图中的某一条边 (x, y, z),有 dist[y] \le dist[x] + z 成立 $$
$$ 则称该边满足三角形不等式。 $$
$$ 若所有边都满足三角形不等式,则 dist 数组就是所求最短路 $$
$$ 下面介绍SPFA算法 $$
const int N = 1e5 + 10, M = 1e6 + 10;
int head[N], ver[M], edge[M], next[M], d[N];
int n, m, tot, s;
std::queue<int> q;
bool v[N];void add(int u, int v, int w) {ver[++tot] = v, edge[tot] = w, next[tot] = head[u], head[u] = tot;
}void spfa(int s) {std::memset(d, 0x3f, sizeof d);d[s] = 0, v[s] = true;q.push(s);while (q.size()) {//取出对头int x = q.front();q.pop();v[x] = false;//扫描所有出边for (int i = head[x]; i; i = next[i]) {int y = ver[i], z = edge[i];if (d[y] > d[x] + z) {//更新,把新的二元组插入堆d[y] = d[x] + z;if (!v[y]) {q.push(y), v[y] = true;}}}}
}相关文章:

算法竞赛进阶指南0x61 最短路
对于一张有向图,我们一般有邻接矩阵和邻接表两种存储方式。对于无向图,可以把无向边看作两条方向相反的有向边,从而采用与有向图一样的存储方式。 $$ 邻接矩阵的空间复杂度为 O(n^2),因此我们一般不采用这种方式 $$ 我们用数组模…...

[学习篇] Autoreleasepool
参考文章: https://www.jianshu.com/p/ec2c854b2efd https://suhou.github.io/2018/01/21/%E5%B8%A6%E7%9D%80%E9%97%AE%E9%A2%98%E7%9C%8B%E6%BA%90%E7%A0%81----%E5%AD%90%E7%BA%BF%E7%A8%8BAutoRelease%E5%AF%B9%E8%B1%A1%E4%BD%95%E6%97%B6%E9%87%8A%E6%94%BE/ …...

晶体基本知识
文章目录晶体基本知识基本概念晶胞<晶格<晶粒<晶体晶胞原子坐标(原子分数坐标)六方晶系与四轴定向七大晶系和十四种点阵结构学习资料吉林大学某实验室教程---知乎系列晶体与压敏器件晶体基本知识 基本概念 晶胞<晶格<…...

免费CRM如何进行选择?
如今CRM领域成为炙手可热的赛道,很多CRM系统厂商甚至打出完全免费的口号,是否真的存在完全免费的crm系统?很多企业在免费使用过程中会出现被迫终止的问题,需要花费高价钱才能继续使用,那么,免费crm系统哪个…...

关于金融类iOS套壳上架,我帮你总结了这些经验
首先说明,本文中出现的案例的,没有特别的专门针对谁,只是用于分析,如有觉得不妥的,请及时联系我删除,鉴于本文发出之后,可能造成的一些影响,所以大家看看就好了,千万不要…...

4年功能测试月薪9.5K,3个月时间成功进阶自动化,跳槽涨薪6k后我的路还很长...
前言 其实最开始我并不是互联网从业者,是经历了一场六个月的培训才入的行,这个经历仿佛就是一个遮羞布,不能让任何人知道,就算有面试的时候被问到你是不是被培训的,我还是不能承认这段历史。我是为了生存,…...

python url解码详解
python url解码 url是数据的一个部分,一般会用来做什么呢?比如网站的 URL,比如搜索引擎中的 url,再比如网页中的图片等。 你也许不知道,在 Web页面中的图片、链接、超链接都是 URL,也就是 url。 而如果想要…...

leetcode102:二叉树的层序遍历
给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。 示例 1: 输入:root [3,9,20,null,null,15,7] 输出:[[3],[9,20],[15,7]] 示例 2: 输入…...
深度学习openMMLab的介绍和使用
文章目录MMCV介绍MMCV的安装修改链接中的cu113修改链接中的torch1.10.0物体分类MMCLS源码下载配置参数解读配置文件的组成如何生成完整配置文件定义自己的数据集构建自己的数据集训练自己的任务物体检测MMDetection语义分割MMSegmentation姿态估计MMPose未完成,持续…...
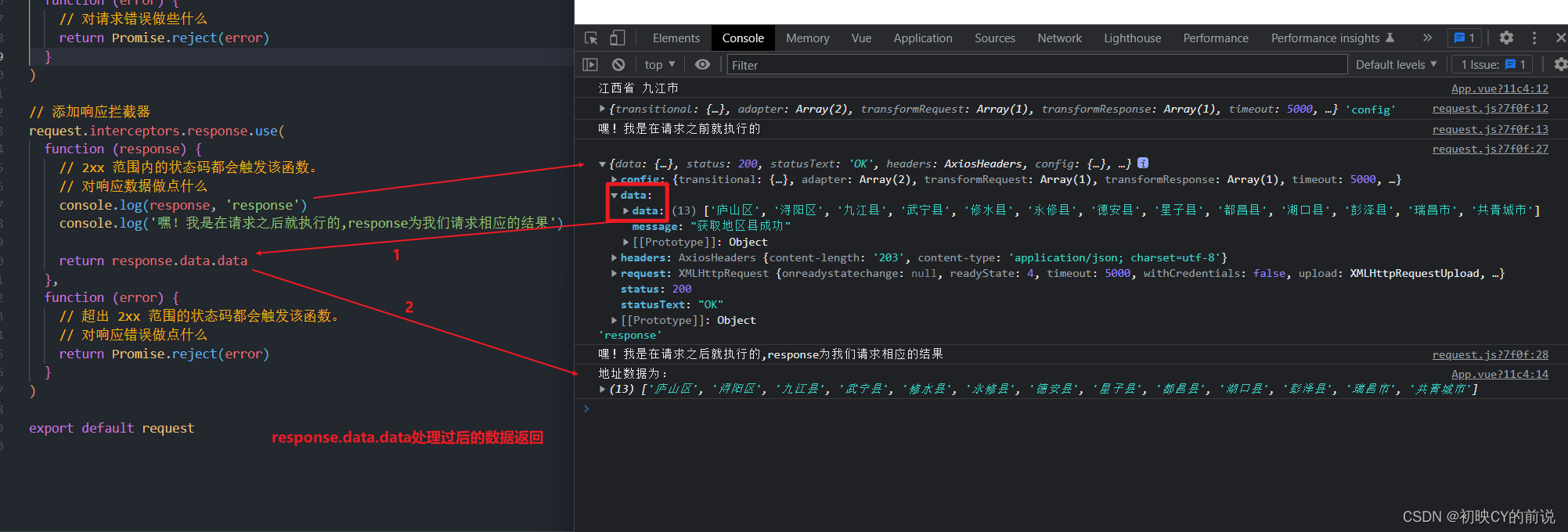
【vue2】axios请求与axios拦截器的使用详解
🥳博 主:初映CY的前说(前端领域) 🌞个人信条:想要变成得到,中间还有做到! 🤘本文核心:当我们在路由跳转前与后我们可实现触发的操作 【前言】ajax是一种在javaScript代码中发请…...

文件上传都发生了啥
一直在用组件库做文件上传,那里面的原理到底是啥,自己写能不能写一个upload框出来呢? (一)基本原理 浏览器端提供了一个表单,在用户提交请求后,将文件数据和其他表单信息编码并上传至服务器端࿰…...

【vim进阶】vim编辑器的多文件操作(如何打开多个文件,如何进行文件间的切换,如何关闭其中的某一个文件)
一、如何打开多个文件? 方法一:启动打开 现在有多个文件 file1 ,file2 , … ,filen. 现在举例打开两个文件 file1,file2 vim file1 file2该方式打开文件,显示屏默认显示第一个文件也就是 file1。 方法二ÿ…...

ToBeWritten之车辆通信
也许每个人出生的时候都以为这世界都是为他一个人而存在的,当他发现自己错的时候,他便开始长大 少走了弯路,也就错过了风景,无论如何,感谢经历 转移发布平台通知:将不再在CSDN博客发布新文章,敬…...

自定义 Jackson 的 ObjectMapper, springboot多个模块共同引用,爽
springboot多个模块共同引用自定义ObjectMapper 🚃统一配置示例自定义 Jackson 的 ObjectMapper更改时区为东八区, 优点是在多个模块中都可以使用同一种方式来进行配置,方便维护和修改 统一配置 假设有一个 Spring Boot 项目,包含多个模块&…...
【面试】Redis面试题
文章目录概述什么是Redis?Redis有哪些优缺点?使用redis有哪些好处?为什么要用 Redis / 为什么要用缓存为什么要用 Redis 而不用 map/guava 做缓存?Redis为什么这么快Redis的应用场景持久化什么是Redis持久化?Redis 的持久化机制是…...

前端后端交互系列之原生Ajax的使用
目录前言一,Ajax概述二,基础知识之Http协议2.1 请求报文2.2 响应报文2.3 如何查看通信报文三,Ajax简单案例3.1 Express框架创建服务端3.2 Ajax案例后台准备3.3 Ajax案例前台准备3.4 发送get请求3.5 发送带有参数的Ajax请求3.6 发送post请求3.…...

openGauss 5.0企业版主从部署,实战狂飙
📢📢📢📣📣📣 哈喽!大家好,我是【IT邦德】,江湖人称jeames007,10余年DBA及大数据工作经验 一位上进心十足的【大数据领域博主】!😜&am…...

Vue中props组件和slot标签的区别
在 Vue 中,props 和 slot 都是组件之间进行通信的机制,它们的作用和应用场景有一些区别: props 是一种组件的数据传递机制,通过在父组件中以属性的形式向子组件传递数据。子组件接收这些数据,并可以进行相应的处理和渲…...

基于Windows下VSCode搭建Vue开发环境
一、准备工作 VSCode编辑器安装:https://code.visualstudio.com/Node.js安装:https://blog.csdn.net/qq_40197828/article/details/78302124VSCode插件安装:Vetur和ESlint 二、更换淘宝镜像源 更换镜像源命令:npm install -g c…...
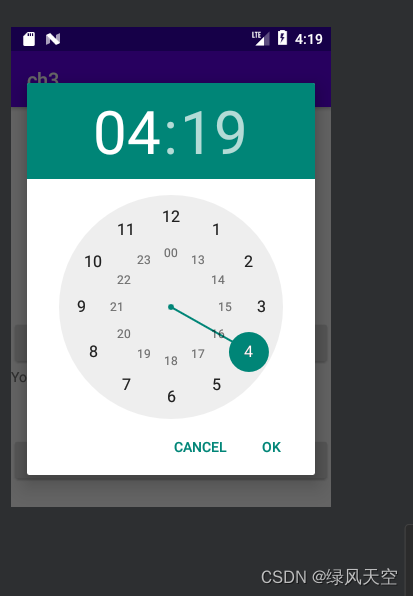
Android开发 Dialog对话框 DatePickerDialog
1. AlertDialog AlertDialog是弹出的提醒对话框,有提示,确认,选择等功能。 没有公开的构造方法,一般用AlertDialog.Builder来完成参数设置,最后调用create方法创建。 参数设置常用的方法: 代码ÿ…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...
