Python | 蓝桥杯进阶第三卷——动态规划

欢迎交流学习~~
专栏: 蓝桥杯Python组刷题日寄
蓝桥杯进阶系列:
🏆 Python | 蓝桥杯进阶第一卷——字符串
🔎 Python | 蓝桥杯进阶第二卷——贪心
💝 Python | 蓝桥杯进阶第三卷——动态规划
✈️ Python | 蓝桥杯进阶第四卷——图论
🌞 Python | 蓝桥杯进阶第五卷——数论
💎 Python | 蓝桥杯进阶第六卷——搜索
Python|蓝桥杯进阶第三卷——动态规划
- 🎁 能量项链
- 🌲 夺宝奇兵
- 🚀 和最大子序列
- 💡 超级玛丽
- 🍞 2^k进制数
🎁 能量项链
题目:
时间限制:
1s
内存限制:
128MB
题目描述:
在Mars星球上,每个Mars人都随身佩带着一串能量项链。在项链上有 N 颗能量珠。能量珠是一颗有头标记与尾标记的珠子,这些标记对应着某个正整数。并且,对于相邻的两颗珠子,前一颗珠子的尾标记一定等于后一颗珠子的头标记。因为只有这样,通过吸盘(吸盘是Mars人吸收能量的一种器官)的作用,这两颗珠子才能聚合成一颗珠子,同时释放出可以被吸盘吸收的能量。如果前一颗能量珠的头标记为 m,尾标记为 r,后一颗能量珠的头标记为 r,尾标记为 n,则聚合后释放的能量为 m*r*n(Mars单位),新产生的珠子的头标记为 m, 尾标记为 n。
需要时,Mars人就用吸盘夹住相邻的两颗珠子,通过聚合得到能量,直到项链上只剩下一颗珠子为止。显然,不同的聚合顺序得到的总能量是不同的,请你设计一个聚合顺序,使一串项链释放出的总能量最大。
例如:设 N=4,4 颗珠子的头标记与尾标记依次为 (2,3) (3,5) (5,10) (10,2)。我们用记号 ◎ 表示两颗珠子的聚合操作,(j◎k) 表示第 j,k两颗珠子聚合后所释放的能量。则第 4、1 两颗珠子聚合后释放的能量为:
(4◎1)=10*2*3=60。
这一串项链可以得到最优值的一个聚合顺序所释放的总能量为
((4◎1)◎2)◎3)=10*2*3+10*3*5+10*5*10=710。
输入描述:
第一行是一个正整数 N(4≤N≤100),表示项链上珠子的个数。
第二行是 N 个用空格隔开的正整数,所有的数均不超过 1000。第 i 个数为第 i 颗珠子的头标记(1≤i≤N),当 i<N 时,第 i 颗珠子的尾标记应该等于第 i+1 颗珠子的头标记。第 N 颗珠子的尾标记应该等于第 1 颗珠子的头标记。
至于珠子的顺序,你可以这样确定:将项链放到桌面上,不要出现交叉,随意指定第一颗珠子,然后按顺时针方向确定其他珠子的顺序。
输出描述:
只有一行,是一个正整数 E(E ≤ 2.1*10^9),为一个最优聚合顺序所释放的总能量
样例输入:
4
2 3 5 10
样例输出:
710
解题思路
针对动态规划类的题目,我们通常采取以下思路:
- 确定
dp数组以及下标的含义- 确定递推公式
- 初始化
dp数组- 确定遍历顺序
接下来的题目我们都会按照这个思路。
确定 dp 数组及其下标的含义:
dp[i][j] 表示第 i 颗珠子到第 j 颗珠子聚合成一颗珠子后所释放的最大能量。
确定递推公式:
dp[i][j] = max(dp[i][k] + dp[k+1][j] + nums[i]*nums[k+1]*nums[j+1]), i≤k<ji\leq k <ji≤k<j, kkk 为断点
这里的
nums[i]表示第i颗珠子的头标记,但注意,项链为环状,我们可以将链状结构复制一份到后方,同时在末尾再加上第1颗珠子的头标记,比如:样例中的2, 3, 5, 10,经过处理后是nums=[2, 3, 5, 10, 2, 3, 5, 10, 2].
注意:从第
k个位置断开(i ~ k已经聚合成了一个珠子且k+1 ~ j也已经聚合成了一个珠子,这个在状态转移的过程中已经处理好了)左右两个珠子聚合得到的能量为nums[i]*nums[k+1]*nums[j+1]
初始化 dp 数组:
都初始化为0即可。
确定遍历顺序:
顺序遍历即可。
参考代码
n = int(input())
nums = list(map(int, input().split())) * 2
nums.append(nums[0])
dp = [[0 for j in range(2*n)] for i in range(2*n)]
res = 0# 递推
# 枚举区间长度
for length in range(1, n):# 枚举区间起点for i in range(2*n):# 计算区间终点j = i + length# 区间终点超出索引,退出if j >= 2*n:break# 枚举区间断点for k in range(i, j):# 状态转移dp[i][j] = max(dp[i][j], dp[i][k]+dp[k+1][j]+nums[i]*nums[k+1]*nums[j+1])# 计算res,最大值res = max(res, dp[i][j])print(res)
🌲 夺宝奇兵
题目:
时间限制:
1s
内存限制:
128MB
题目描述:
在一座山上,有很多很多珠宝,它们散落在山底通往山顶的每条道路上,不同道路上的珠宝的数目也各不相同.下图为一张藏宝地图:
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
”夺宝奇兵”从山下出发,到达山顶,如何选路才能得到最多的珠宝呢?(每次只能直上或左上)
在上图所示例子中,按照 5-> 7-> 8-> 3-> 7 的顺序,将得到最大值 30.
输入描述:
第一行正整数 N(100 >= N >1),表示山的高度
接下来有 N 行非负整数,第 i 行有 i 个整数 (1 <= i <=N),表示山的第 i 层上从左到右每条路上的珠宝数目。
输出描述:
一个整数,表示从山底到山顶的所能得到的珠宝的最大数目.
样例输入:
5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
样例输出:
30
解题思路
确定 dp 数组及其下标的含义:
dp[i][j] 表示位置 i,j 对应的珠宝最大数目。
确定递推公式:
dp[i][j] = max(dp[i-1][j] + cell[i][j], dp[i-1][j-1] + cell[i][j])
初始化 dp 数组:
都初始化为0即可。
确定遍历顺序:
从上往下遍历即可。
参考代码
n = int(input())
# cell 为每个位置的珠宝数目
cell = []
for i in range(n):cell.append(list(map(int, input().split())))
# dp[i][j] 表示位置 i,j 对应的珠宝最大数目
dp = [[0 for j in range(n)] for i in range(n)]
dp[0][0] = cell[0][0]
# 从上往下遍历
for i in range(n):for j in range(i+1):dp[i][j] = max(dp[i-1][j] + cell[i][j], dp[i-1][j-1] + cell[i][j])# 最后一层的最大值
res = max(dp[-1])
print(res)
🚀 和最大子序列
题目:
时间限制:
1s
内存限制:
128MB
题目描述:
对于一个给定的长度为 N 的整数序列 A,它的“子序列”的定义是:A 中非空的一段连续的元素(整数)。你要完成的任务是,在所有可能的子序列中,找到一个子序列,该子序列中所有元素的和是最大的(跟其他所有子序列相比)。程序要求你输出这个最大值。
输入描述:
输入文件的第一行包含一个整数 N,第二行包含 N 个整数,表示 A。
其中
1 < = N < = 100000
-10000 <= A[i] <= 10000
输出描述:
输出仅包含一个整数,表示你算出的答案。
样例输入:
5
3 -2 3 -5 4
样例输出:
4
解题思路
确定 dp 数组及其下标的含义:
dp[i] 表示序列 nums[:i+1] 的子序列的最大和。
确定递推公式:
dp[i] = max(dp[i-1]+nums[i], nums[i])
初始化 dp 数组:
初始化为 nums[0] 即可。
确定遍历顺序:
顺序遍历即可。
参考代码
n = int(input())
nums = list(map(int, input().split()))
print(nums[:1])
# dp[i] 表示序列 nums[:i+1] 的子序列的最大和
dp = [nums[0] for i in range(n)]
for i in range(1, len(nums)):dp[i] = max(dp[i-1]+nums[i], nums[i])
print(max(dp))
💡 超级玛丽
题目:
时间限制:
1s
内存限制:
128MB
题目描述:
大家都知道" 超级玛丽" 是一个很善于跳跃的探险家,他的拿手好戏是跳跃,但它一次只能向前跳一步或两步。有一次,他要经过一条长为 n 的羊肠小道,小道中有 m 个陷阱,这些陷阱都位于整数位置,分别是 a1,a2,....,ama1,a2,...., ama1,a2,....,am,陷入其中则必死无疑。显然,如果有两个挨着的陷阱,则玛丽是无论如何也跳过不去的。
现在给出小道的长度 n,陷阱的个数及位置。求出玛丽从位置 1 开始,有多少种跳跃方法能到达胜利的彼岸(到达位置 n)。
输入描述:
第一行为两个整数 n,m
第二行为 m 个整数,表示陷阱的位置
数据规模和约定
40 >= n >= 3, m >= 1
n > m;
陷阱不会位于 1 及 n 上
输出描述:
一个整数。表示玛丽跳到 n 的方案数
样例输入:
4 1
2
样例输出:
1
解题思路
确定 dp 数组及其下标的含义:
dp[i] 表示到达位置 i 的跳跃方法数。
确定递推公式:
当满足:index.count(i) == 0 即此处没有陷阱, dp[i] = dp[i-j] + dp[i]
初始化 dp 数组:
初始化为 0 即可。
确定遍历顺序:
顺序遍历即可。
参考代码
n, m = map(int, input().split())
index = list(map(int, input().split()))
# dp[i] 表示到达位置 i 的跳跃方法数
# dp[0] = 0 便于后续处理
dp = [0 for i in range(n+1)]
dp[1] = 1
for i in range(2, n+1):for j in [1, 2]:# 判断前两个位置是否有陷阱if index.count(i) == 0:dp[i] = dp[i-j] + dp[i]
print(dp[-1])
🍞 2^k进制数
题目:
时间限制:
1s
内存限制:
128MB
题目描述:
设 rrr 是个 2k2^k2k 进制数,并满足以下条件:
- rrr 至少是个 222 位的 2k2^k2k 进制数。
- 作为 2k2^k2k 进制数,除最后一位外,rrr 的每一位严格小于它右边相邻的那一位。
- 将 rrr 转换为 222 进制数 qqq 后,则 qqq 的总位数不超过 www。
在这里,正整数 k(1≤k≤9)k(1≤k≤9)k(1≤k≤9)和 w(k<w≤30000)w(k<w≤30000)w(k<w≤30000) 是事先给定的。
问:满足上述条件的不同的 rrr 共有多少个?
我们再从另一角度作些解释:设 SSS 是长度为 www 的 01字符串(即字符串 SSS 由 www 个0或1组成),SSS 对应于上述条件中的 qqq。将 SSS 从右起划分为若干个长度为 kkk 的段,每段对应一位2k2^k2k 进制的数,如果 SSS 至少可分成 222 段,则 SSS 所对应的二进制数又可以转换为上述的 2k2^k2k 进制数 rrr。
例:设 k=3,w=7k=3,w=7k=3,w=7。则 rrr 是个八进制数 (23=8)(2^3=8)(23=8)。由于 w=7w=7w=7,长度为 7 的 01 字符串按 3位一段分,可分为 3 段(即1,3,3,左边第一段只有一个二进制位),则满足条件的八进制数有:
2位数:
高位为1:6 个(即 12,13,14,15,16,17 ),高位为 2:5 个,…,高位为6:1个(即67 )。共 6+5+…+1=21 个。
3位数:
高位只能是1,第 2 位为 2 :5 个(即123,124,125,126,127),第2位为3:4个,…,第 2 位为 6:1个(即 167)。共5+4+…+1=15个。
所以,满足要求的 rrr 共有 36个。
输入描述:
只有1行,为两个正整数,用一个空格隔开:
kkk www
输出描述:
1行,是一个正整数,为所求的计算结果,即满足条件的不同的 rrr 的个数(用十进制数表示),要求最高位不得为0,各数字之间不得插入数字以外的其他字符(例如空格、换行符、逗号等)。
(提示:作为结果的正整数可能很大,但不会超过200位)
样例输入:
3 7
样例输出:
36
解题思路
确定 dp 数组及其下标的含义:
dp[i][j] 表示有 (i+1) 位数字,最高位数字是 j 时满足条件的数字个数。
确定递推公式:
若 j!=0 :dp[i][j] = dp[i-1][j+1]+dp[i-1][j+2]+dp[i-1][j+3]······
也就是说最高位不是0的时候,满足条件的数字个数是,第二高位的数字大于最高位的数字的情况的和。
若j==0:dp[i][j] = dp[i-1][j]+dp[i-1][j+1]+dp[i-1][j+2]+dp[i-1][j+3]······
如果最高位是 0,那么第二高位数字则可以取0。也就比上一个情况多加了个 dp[i-1][j]。
初始化 dp 数组:
dp[0][j]=1 即只有一位数字时只有一种情况
确定遍历顺序:
顺序遍历即可。
此外注意最终结果的计算和处理,具体见代码。
参考代码
import math
k, w = map(int, input().split())
# rows, cols 为dp数组的行数和列数
rows, cols = w//k+1, 2**k
# i 是 2^k 进制下数字的位数
# j 是 每一位上可以取到的值
# dp[i][j] 表示有 (i+1) 位数字,最高位数字是 j 时满足条件的数字个数
dp = [[0 for j in range(cols)] for i in range(rows)]
# 初始化 res,为结果
res = 0# dp 数组初始化
# dp[0][j] 表示有 1 位数字的情况
for j in range(cols):dp[0][j] = 1# 递推
for i in range(1, rows):for j in range(cols):dp[i][j] = sum(dp[i-1][j+1:])if j == 0:dp[i][j] += dp[i-1][j]# 计算最后的结果
if w%k == 0:# 此时最高位可以取 0 到 cols, 即最后一行所有情况都可以用res = sum(dp[-1])
else:# 此时最高位只能取 0 到 2**(w%k)-1res = sum(dp[-1][:2**(w%k)])# 题目中要求位数 >= 2
# 需要减去只有一位数的情况
if w/k <= 1:res = 0
else:res -= 2**k
print(res)
相关文章:

Python | 蓝桥杯进阶第三卷——动态规划
欢迎交流学习~~ 专栏: 蓝桥杯Python组刷题日寄 蓝桥杯进阶系列: 🏆 Python | 蓝桥杯进阶第一卷——字符串 🔎 Python | 蓝桥杯进阶第二卷——贪心 💝 Python | 蓝桥杯进阶第三卷——动态规划 ✈️ Python | 蓝桥杯进阶…...

蓝桥杯31天真题冲刺|题解报告|第二十九天
大家好,我是snippet,今天是我们刷题的第二十九天,今天主打打比赛,牛客AcWing力扣,今天的牛客是真的有趣,下面是我今天AcWing周赛的题解 目录 一、热身计算 题目链接:4944. 热身计算 - AcWing题…...

[Rust GUI]fltk-rs的helloworld
1、安装VSCode 下载安装VSCode 安装VSCode扩展 rust-analyzer或rust-analyzer(CN) 2、安装Microsoft C 生成工具 访问微软官网下载生成工具,勾选使用 C 的桌面开发之后会自动勾选5个项目 取消勾选以下项目 用于 Windows 的 C CMake 工具 测试工具核心功能 - 生成…...

蓝桥杯真题05
重新排序 问题描述 给定一个数组 A 和一些查询 Li,Ri 求数组中第 Li 至第 Ri个元素之和。 小蓝觉得这个问题很无聊, 于是他想重新排列一下数组, 使得最终每个查询结果的和尽可能地大。小蓝想知道相比原数组, 所有查询结果的总和最多可以增加多少? 输入格式 输入第一行包含…...
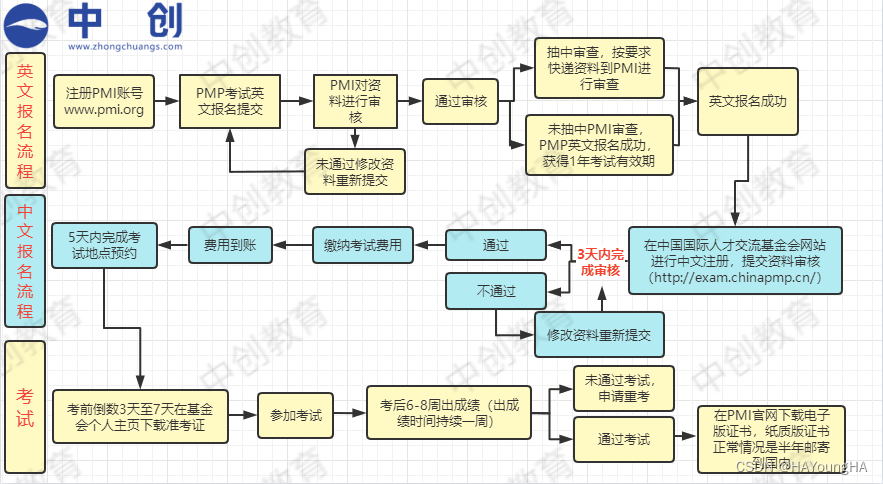
PMP那些事儿,备考小白看过来
一、PMP是什么? PMP指的是项目管理专业人士资格认证。它是由美国项目管理协会(Project Management Institute(PMI)发起的,严格评估项目管理人员知识技能是否具有高品质的资格认证考试。 其目的是为了给项目管理人员提供统一的行业标准。目前࿰…...
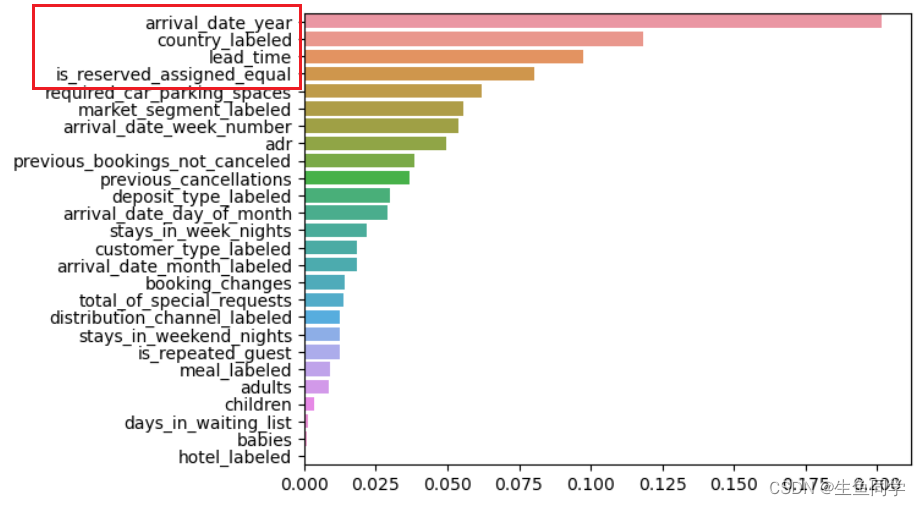
【数据分析实战】基于python对酒店预订需求进行分析
文章目录📚引言📖数据加载以及基本观察📑缺失值观察及处理🔖缺失值观察以及可视化🔖缺失值处理📖用户数据探索📑什么时间预定酒店将会更经济实惠?📑哪个月份的酒店预订是…...

【新2023Q2模拟题JAVA】华为OD机试 - 数组的中心位置
最近更新的博客 华为od 2023 | 什么是华为od,od 薪资待遇,od机试题清单华为OD机试真题大全,用 Python 解华为机试题 | 机试宝典【华为OD机试】全流程解析+经验分享,题型分享,防作弊指南华为od机试,独家整理 已参加机试人员的实战技巧本篇题解:数组的中心位置 题目 给你一…...

Vue的props组件详解
const props defineProps({name: String, }); String 是在 defineProps() 函数中用来声明 name prop 的类型,表示 name 必须是字符串类型。如果父组件没有传入 name 或传入的 name 不是字符串类型,那么就会产生类型验证错误。 defineProps() 函数支持…...
抽烟行为识别预警系统 yolov5
抽烟行为识别预警系统基于yolov5网络模型智能分析技术,抽烟行为识别预警算法通过监测现场人员抽烟行为自动存档进行报警提示。我们选择当下YOLO卷积神经网络YOLOv5来进行抽烟识别检测。6月9日,Ultralytics公司开源了YOLOv5,离上一次YOLOv4发布…...

【0基础学爬虫】爬虫基础之文件存储
大数据时代,各行各业对数据采集的需求日益增多,网络爬虫的运用也更为广泛,越来越多的人开始学习网络爬虫这项技术,K哥爬虫此前已经推出不少爬虫进阶、逆向相关文章,为实现从易到难全方位覆盖,特设【0基础学…...

airflow源码分析-任务调度器实现分析
Airflow源码分析-任务调度器实现分析 概述 本文介绍Airflow执行器的总体实现流程。通过函数调用的方式说明了Airflow scheduler的实现原理,对整个调度过程的源码进行了分析。 通过本文,可以基本把握住Airflow的调度器的运行原理主线。 启动调度器 可…...
和reduceRight())
一文学会数组的reduce()和reduceRight()
reduce()方法和reduceRight()方法依次处理数组的每个成员,最终累计为一个值。 它们的差别是,reduce()是从左到右处理,reduceRight()则是从右到左,其他完全一样。 [1, 2, 3, 4, 5].reduce(function (a, b) {console.log(a, b);ret…...
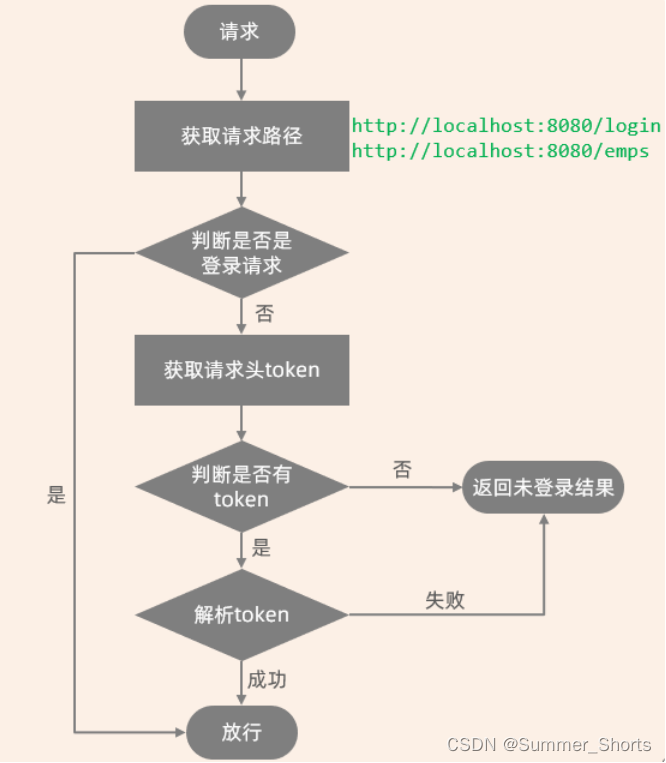
登录校验-Filter
上一篇介绍完了基础应用和细节,现在来完成登录校验功能基本流程: 要进入后台管理系统,必须完成登录操作,此时就需要访问登录接口Login。登录成功服务端会生成一个JWT令牌,并且返回给前端,前端会将JWT令牌存…...

C C++ Java python 分别写出不同表白girlfriend的爱心动态代码实现
C `` #include <stdio.h> #include <stdlib.h> #include <windows.h> void heart_animation() {int i, j, k; for (i = 1; i <= 6; i++) {for (j = -3; j <= 3; j++) {for (k = -4; k <= 4; k++) {if (abs(j) + abs(k) < i * 2) {printf(“I”)…...

ThreeJS-投影、投影模糊(十七)
无投影: 完整的代码: <template> <div id"three_div"></div> </template> <script> import * as THREE from "three"; import { OrbitControls } from "three/examples/jsm/controls/Or…...
)
蓝桥杯赛前冲刺-枚举暴力和排序专题1(包含历年蓝桥杯真题和AC代码)
目录 连号区间数(第四届蓝桥杯省赛CB组,第四届蓝桥杯省赛JAVAB组) 递增三元组(第九届蓝桥杯省赛CB组,第九届蓝桥杯省赛JAVAB组) 特别数的和(第十届蓝桥杯省赛CB组,第十届蓝桥杯省赛JAVAB组) 错误票据&a…...
Github库中的Languages显示与修改
目录 前言 【.gitattributes】文件 修改GitHub语言 前言 上传一个项目到GitHub时,发现显示的语言并非是自己项目所示的语言,这样的情况是经常发生的,为了能到达自己所需快速检索,或者是外部访问者能很好的搜索我们的项目&#…...

RocketMQ消息高可靠详解
文章目录 消息同步策略殊途同归同步基于offset而不是消息本身刷盘策略RocketMQ broker服务端以组为单位提供服务的,拥有着一样的brokerName则认为是一个组。其中brokerId=0的就是master,大于0的则为slave。 消息同步策略 master和slave都可以提供读服务,但是只有master允许…...

【python设计模式】4、建造者模式
哲学思想: 建造者模式的哲学思想是将复杂对象的创建过程分解成多个简单的步骤,并将这些步骤分别封装在一个独立的建造者类中。然后,我们可以使用一个指挥者类来控制建造者的调用顺序,以便在每个步骤完成后正确地构建复杂对象。 …...

【全网独家】华为OD机试Golang解题 - 机智的外卖员
华为Od必看系列 华为OD机试 全流程解析+经验分享,题型分享,防作弊指南华为od机试,独家整理 已参加机试人员的实战技巧华为od 2023 | 什么是华为od,od 薪资待遇,od机试题清单华为OD机试真题大全,用 Python 解华为机试题 | 机试宝典使用说明 如果想要在华为od机试中获取高分…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

从“安全密码”到测试体系:Gitee Test 赋能关键领域软件质量保障
关键领域软件测试的"安全密码":Gitee Test如何破解行业痛点 在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的"神经中枢"。从国防军工到能源电力,从金融交易到交通管控,这些关乎国计民生的关键领域…...

《Offer来了:Java面试核心知识点精讲》大纲
文章目录 一、《Offer来了:Java面试核心知识点精讲》的典型大纲框架Java基础并发编程JVM原理数据库与缓存分布式架构系统设计二、《Offer来了:Java面试核心知识点精讲(原理篇)》技术文章大纲核心主题:Java基础原理与面试高频考点Java虚拟机(JVM)原理Java并发编程原理Jav…...
