【1017. 负二进制转换】
来源:力扣(LeetCode)
描述:
给你一个整数 n ,以二进制字符串的形式返回该整数的 负二进制(base -2)表示。
注意, 除非字符串就是 "0",否则返回的字符串中不能含有前导零。
示例 1:
输入:n = 2
输出:"110"
解释:(-2)2 + (-2)1 = 2
示例 2:
输入:n = 3
输出:"111"
解释:(-2)2 + (-2)1 + (-2)0 = 3
示例 3:
输入:n = 4
输出:"100"
解释:(-2)2 = 4
提示:
- 0 <= n <= 109
方法一:模拟进位
思路与算法
对于「二进制数」我们可以很直观地得到以下结论:
- 对于 2i,如果 i 为偶数时,此时 2i = (−2)i;
- 对于 2i,如果 i 为奇数时,此时 2i = (−2)i+1 + (−2)i;
因此自然可以想到将 n 转换为 −2 的幂数和,即此时 n= ∑i=0m\sum_{i=0}^m∑i=0m C×(−2)i,由于 −2 进制的每一位只能为 0 或 1,需要对每一位进行加法「进位」运算即可得到完整的「负二进制」数。对于「负二进制」数,此时需要思考一下进位规则。对于 C×(−2)i,期望得到如下变换规则:
-
如果 C 为奇数则需要将等式变为 C × (−2)i = a × (−2)i+1 + (−2)i,此时第 i 位为 1,第 i + 1 位需要加上 a;
-
如果 C 为偶数则需要将等式变为 C × (−2)i = a × (−2)i+1 ,此时第 i 位为 0,第 i + 1 位需要加上 a;
根据以上的变换规则,只需要求出 a 即可。假设当前数位上的数字为 val,当前的位上保留的余数为 r,在 x 进制下的进位为 a,根据「进位」的运算规则可知 val = a × x + r,此时可以得到进位 a = val−rx\frac{val - r} {x}xval−r。根据题意可知,「负二进制」数的每一位上保留的余数为 0 或 1,因此可以计算出当前的余数 r,由于在有符号整数的均采用补码表示,最低位的奇偶性保持不变,因此可以直接取 val 的最低位即可,此时可以得到 r = val & 1。根据上述等式可以知道,当前数位上的数字为 val 时,此时在「负二进制」下向高位的进位为 a = val−(val&1)−2\frac{val - (val \& 1)} {-2}−2val−(val&1) 。
基于以上进位规则,将变换出来的数列进行进位运算即可得到完整的「负二进制」数。整个转换过程如下:
- 将 n 转换为二进制数,并将二进制数中的每一位转换为「负二进制」中的每一位,变换后的数列为 bits;
- 将 bits 从低位向高位进行「进位」运算,即将 bits 中的每一位都变为 0 或者 1;
- 去掉前导 0 以后,将 bits 转换为字符串返回即可。
代码:
class Solution {
public:string baseNeg2(int n) {if (n == 0) {return "0";}vector<int> bits(32);for (int i = 0; i < 32 && n != 0; i++) {if (n & 1) {bits[i]++;if (i & 1) {bits[i + 1]++;}}n >>= 1;}int carry = 0;for (int i = 0; i < 32; i++) {int val = carry + bits[i];bits[i] = val & 1;carry = (val - bits[i]) / (-2);}int pos = 31;string res;while (pos >= 0 && bits[pos] == 0) {pos--;}while (pos >= 0) {res.push_back(bits[pos] + '0');pos--;}return res;}
};
执行用时:0 ms, 在所有 C++ 提交中击败了100.00%的用户
内存消耗:5.9 MB, 在所有 C++ 提交中击败了33.33%的用户
复杂度分析
时间复杂度:O( C ),其中 C = 32。需要对 n 转换为二进制位,需要的时间复杂度为 O(logn),然后需要对其进行二进制位的中每一位进行「负二进制进位」运算,由于整数有 32 位,因此需要「负二进制进位」运算 32 次即可。
空间复杂度:O( C ),其中 C = 32。需要对 n 转换为二进制位,由于整数最多只有 32 位,在此每次采取固定的存储空间为 O(32)。
方法二:进制转换
思路与算法
当基数 x > 1 时,将整数 n 转换成 x 进制的原理是:令 n0 = n,计算过程如下:
- 当计算第 0 位上的数字时,此时 n1 = ⌊ n0x{n_0} \over xxn0⌋,n0 = n1 × x + r,其中 0 ≤ r < x;
- 当计算第 i 位上的数字时,此时 ni+1 = ⌊ nix{n_i} \over xxni ⌋,ni = ni+1 × x + r,其中 0 ≤ r < x;
按照上述计算方式进行计算,直到满足 ni = 0 结束。
如果基数 x 为负数,只要能确定余数的可能取值,上述做法同样适用。由于「负二进制」表示中的每一位都是 0 或 1,因此余数的可能取值是 0 和 1,可以使用上述做法将整数 n 转换成「负二进制」。具体转换过程如下:
- 如果 n = 0 则返回 “0",n = 1 则直接返回 “1";
- 如果 n > 1 则使用一个字符串记录余数,将整数 n 转换成「负二进制」,重复执行如下操作,直到 n = 0;
- 计算当前 n 的余数,由于当前的余数只能为 0 或 1,由于有符号整数均采用补码表示,最低位的奇偶性保持不变,因此可以直接取 C 的最低位即可,此时直接用 n&1 即可得到最低位的余数,将余数拼接到字符串的末尾。
- 将 n 的值减去余数,然后将 n 的值除以 −2。
上述操作结束之后,将字符串翻转之后得到「负二进制」数。
代码:
class Solution {
public:string baseNeg2(int n) {if (n == 0 || n == 1) {return to_string(n);}string res;while (n != 0) {int remainder = n & 1;res.push_back('0' + remainder);n -= remainder;n /= -2;}reverse(res.begin(), res.end());return res;}
};
执行用时:0 ms, 在所有 C++ 提交中击败了100.00%的用户
内存消耗:5.8 MB, 在所有 C++ 提交中击败了75.00%的用户
复杂度分析
时间复杂度:O(logn),其中 n 是给定的整数。整数 n 对应的「负二进制」表示的长度是 logn,需要生成「负二进制」表示的每一位。
空间复杂度:O(1)。除返回值外,不需要额外的空间。
方法三:数学计算
思路与算法
根据题意可知,32 位「负二进制」数中第 i 位则表示(−2)i,当 i 为偶数时,则 (−2)i = 2i,当 i 为奇数时,则 (−2)i = −2i ,因此可以得到其最大值与最小值分别为如下:
- 最大值即所有的偶数位全部都为 1,奇数位全为 0,最大值即为 0x55555555 = 1,431,655,765;
- 最小值即所有的偶数位全部都为 0,奇数位全为 1,最小值即为 0xAAAAAAAA = −2,863,311,530;
- 0x55555555, 0xAAAAAAAA 均为「十六进制」进制原码表示;
令 maxVal = 0x55555555,由于题目中 n 给定的范围为 0 ≤ n ≤ 109,因此一定满足 maxVal > n。设 maxVal 与 n 的差为 diff,则此时 diff = maxVal − n,如果我们将 maxVal 在「负二进制」表示下减去 diff,那么得到的「负二进制」一定为 n 的「负二进制」。已知 maxVal 中的偶数位全为 1,奇数位全为 0,此时的减法操作可以用异或来实现:
- 对于 diff 中偶数位为 1 的位,在 maxVal 中需要将其置为 0,此时 maxVal 中偶数位全部为 1,1 ⊕ 1 = 0,偶数位异或操作即可将需要的位置为 0;
- 对于 diff 中奇数位为 1 的位,在 maxVal 中需要将其置为 1,此时 maxVal 中奇数位全部为 0,0 ⊕ 1 = 1,奇数位异或操作将需要的位置为 1,
根据以上推论可以知道,「负二进制」减法等同于 maxVal ⊕ diff。按照上述方法可以知道 n 的「负二进制」数等于 ma x Val ⊕ (maxVal − n),我们求出 n 的「负二进制」数,然后将其转换为二进制的字符串即可。
代码:
class Solution {
public:string baseNeg2(int n) {int val = 0x55555555 ^ (0x55555555 - n);if (val == 0) {return "0";}string res;while (val) {res.push_back('0' + (val & 1));val >>= 1;}reverse(res.begin(), res.end());return res;}
};
执行用时:0 ms, 在所有 C++ 提交中击败了100.00%的用户
内存消耗:5.7 MB, 在所有 C++ 提交中击败了98.15%的用户
复杂度分析
时间复杂度:O(logn),其中 n 是给定的整数。整数 n 对应的「负二进制」表示的长度是 logn,需要生成「负二进制」表示的每一位。
空间复杂度:O(1)。除返回值外,不需要额外的空间。
author:LeetCode-Solution
相关文章:

【1017. 负二进制转换】
来源:力扣(LeetCode) 描述: 给你一个整数 n ,以二进制字符串的形式返回该整数的 负二进制(base -2)表示。 注意, 除非字符串就是 "0",否则返回的字符串中不…...

C语言实现插入排序与希尔排序
目录 一,插入排序 插入排序C语言实现(升序) 1,将新元素插入到有序序列 2,循环的开始与终止 二,希尔排序 希尔排序C语言实现(升序) 1,单趟: 2&#x…...

第九章-DOM与CSS
style属性 文档中每个元素节点都有一个属性style。style属性包含着元素样式,查询这个属性将返回一个对象而不是一个简单的字符串。样式都存放在这个style对象的属性里。 var element getElementById("example") //查看颜色属性 element.style.color //…...

蓝桥杯真题练习
小蓝在玩一个寻宝游戏, 游戏在一条笔直的道路上进行, 道路被分成了 nn 个方格, 依次编号 1 至 nn, 每个方格上都有一个宝物, 宝物的分值是一个整数 (包括正数、负数和零), 当进入一个方格时即获得方格中宝物的分值。小蓝可 以获得的总分值是他从方格中获得的分值之和。 小蓝开始…...

插入排序的简单理解
详细描述 插入排序的基本思想是:将一个记录插入到已经排好序的有序表中,从而得到一个新的、记录数增 1 的有序表。 在其实现过程中使用双层循环,外层循环针对除了第一个元素之外的所有元素,内层循环针对当前元素前面的有序表进行…...

Springboot框架集成Websocket通信方式
Websocket实现了“服务器”主动向“客户端”发送数据,改变了以往通过轮询、长轮训、长连接等方式获取服务器端数据的方式。 一、Websocket有三种不同的用场景,单播、广播和组播; (一)、单播(Unicast) 单播是客户端与服务器之间的“一对一”的连接。是在一个单个的发送…...

将json数据分组
在工作中有时需要根据业务需要,将大量数据进行处理分成几个一组 // 例如要将下方数据进行处理 var stuCount [{"id": "1612321835288","libraryCode": "D","regionCode": "A","positionCode&qu…...

从零开始实现一个C++高性能服务器框架----Socket模块
此项目是根据sylar框架实现,是从零开始重写sylar,也是对sylar丰富与完善 项目地址:https://gitee.com/lzhiqiang1999/server-framework 简介 项目介绍:实现了一个基于协程的服务器框架,支持多线程、多协程协同调度&am…...

ld: library not found for -lcrt0.o
ld: library not found for -lcrt0.o 背景: Mac 系统编译的时候报错 语言:golang 原因: 代码使用了静态编译,-static。stack overflow 上说 This option will not work on Mac OS X unless all libraries (including libgcc.a…...
接口测试和功能测试的区别有哪些?说一些你不知道的知识
目录 接口测试和功能测试的区别 目的 测试范围 测试方法 重要性 编辑 举个例子 对于接口测试 对于功能测试 编辑 总结 接口测试和功能测试是软件测试中的两种常见测试类型,主要用于评估软件系统的质量。尽管这两种测试都是为了评估软件系统的性…...
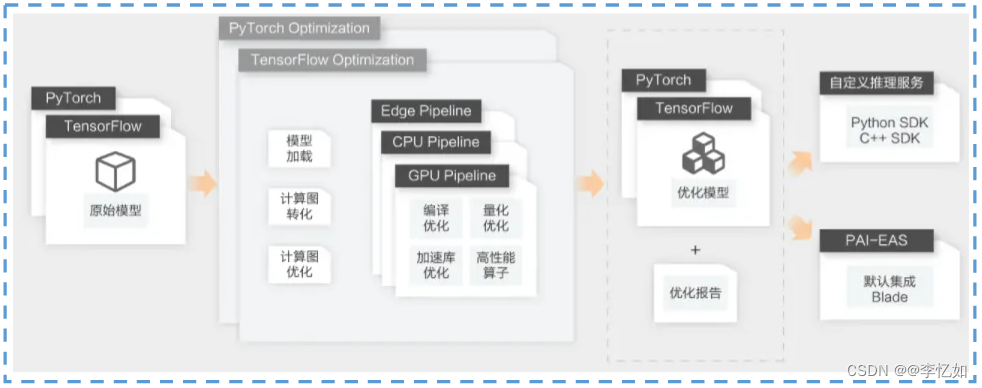
深度学习实战——不同方式的模型部署(CNN、Yolo)
忆如完整项目/代码详见github:https://github.com/yiru1225(转载标明出处 勿白嫖 star for projects thanks) 目录 系列文章目录 一、实验综述 1.实验工具及及内容 2.实验数据 3.实验目标 4.实验步骤 二、ML/DL任务综述与模型部署知识…...

【论文阅读】GNN阅读笔记
A gentle introduction on gnn 前言 发表在distill的文章 图神经网络在应用上才刚刚开始 搭建了一个GNN playground 什么是图 图是表示实体之间的关系 可以分别表示成点向量、边向量、图向量 图可以分为有向图和无向图 数据是怎么表示成图 图片表示成图: …...
,QTableWidget控件)
QT常用控件——QTreeWidget(树控件),QTableWidget控件
目录 ★先开个小灶,在此插句话:【有关Halcon与Qt联编变量转换】 QTreeWidget树控件 QTableWidget控件...

为什么学校购买小型数控机床而不是大型工业数控机床?
CNC 机器是计算机控制的设备,可以高精度和准确度地切割、雕刻、钻孔或雕刻各种材料。 它们广泛应用于制造、工程、设计和艺术行业。 CNC 机器具有不同的尺寸和功能,从小型台式机到大型工业机型。 人们可能想知道为什么学校会选择购买小型 CNC 机器而不是…...

【Go自学】一文搞懂Go append方法
我们先看一下append的源码 // The append built-in function appends elements to the end of a slice. If // it has sufficient capacity, the destination is resliced to accommodate the // new elements. If it does not, a new underlying array will be allocated. //…...
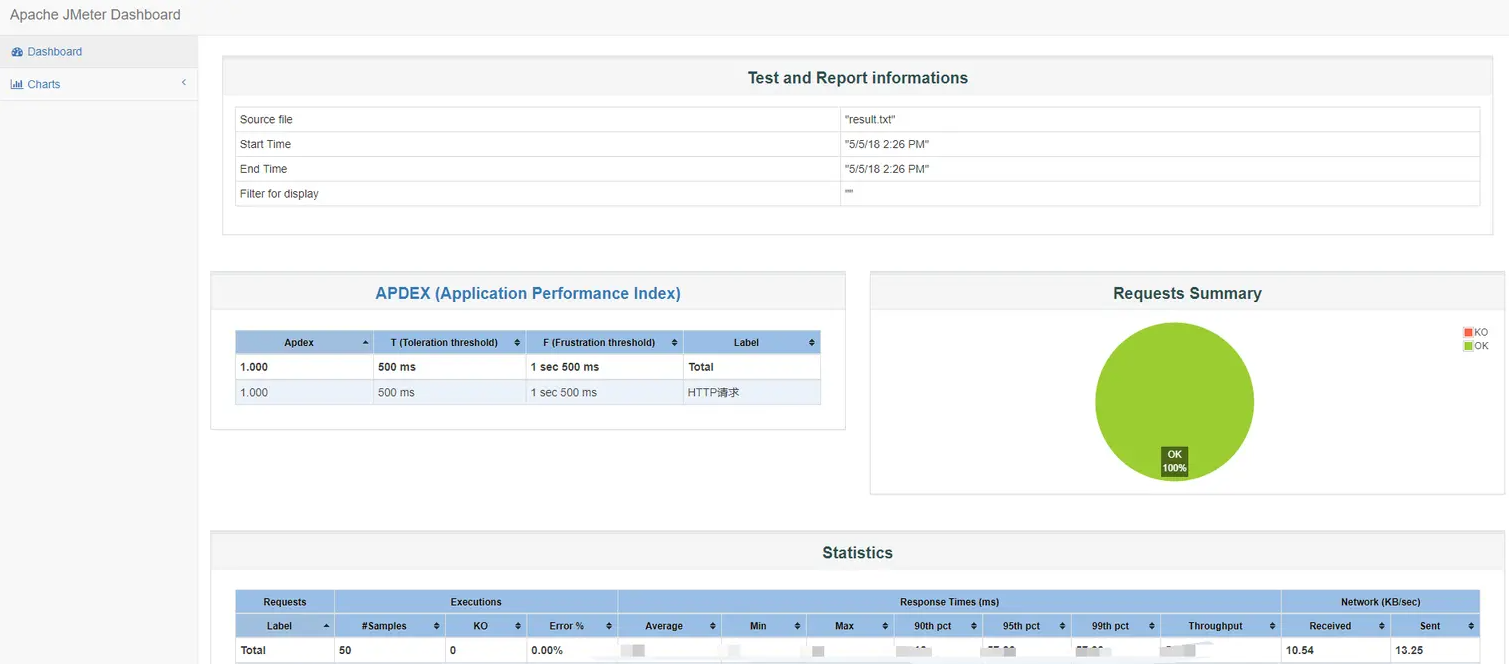
【压测】通过Jemeter进行压力测试(超详细)
文章目录背景一、前言二、关于JMeter三、准备工作四、创建测试4.1、创建线程组4.2、配置元件4.3、构造HTTP请求4.4、添加HTTP请求头4.5、添加断言4.6、添加察看结果树4.7、添加Summary Report4.8、测试计划创建完成五、执行测试计划总结背景 通过SpringCloudGateway整合Nacos进…...
加密算法)
C# | 上位机开发新手指南(七)加密算法
上位机开发新手指南(七)加密算法 文章目录上位机开发新手指南(七)加密算法前言加密算法的分类对称加密算法和非对称加密算法流加密算法和块加密算法分组密码和序列密码哈希函数和消息认证码对称加密与非对称对称加密优点缺点对称加…...
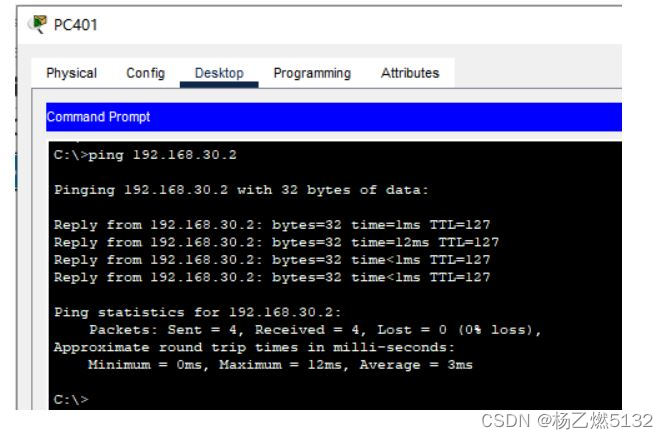
实验一 跨VLAN访问
目录 一、按照拓扑图配置VLAN,并实现跨VLAN间的访问。 二、实验环境 三、实验步骤 一、按照拓扑图配置VLAN,并实现跨VLAN间的访问。 1、配置好交换机的VLAN和各个终端的地址,实现各个VLAN内能连通。 2、开启两个交换机的VTY连接࿰…...

通信算法之130:软件无线电-接收机架构
1. 超外差式接收机 2.零中频接收机 3.数字中频接收机...

C++编程大师之路:从入门到精通-C++基础入门
文章目录前言主要内容C基础入门初识C第一个C程序注释变量常量关键字标识符命名规则数据类型整型sizeof关键字实型(浮点型)字符型转义字符字符串型布尔类型 bool数据的输入运算符算术运算符赋值运算符比较运算符逻辑运算符程序流程结构选择结构if语句三目…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...
