想要的古风女生头像让你快速get
如今我看到很多人都喜欢用古风女生当作头像,那么今天我就来教大家如何快速得到一张超美的古风女生头像~

上图就是我使用 APISpace 的 AI作画(图像生成)服务 快速生成的古风女生头像,不仅可以限定颜色,还可以选择『宝石镶嵌』或『花卉造型』这样的细节修饰词!小说插画、聊天头像、绘画参考,超多场景都可以使用。
描述语 : artstation , pixiv ,韩系,古风女生,宝石发簪,头像,华丽背景。
试着使用上面的文字描述 ,马上就可以生成『朱唇一点桃花殷,宿妆娇羞偏善囊』的古风少女哦!
好了~现在就来教大家如何get古风女生头像!
1.注册登录 APISpace 后,进入 【AI作画详情页】,领取【免费流量】
2.点击【测试API】,根据参数提示,填写好相应的参数值
3.将返回参数的key值复制填写至【获取生成图片API】的参数值中,请求即可获得图片
AI作画 接口参数说明:
- prompt:生成图片的关键词,图像进行描述,有内容风格等信息进行描述,支持中英文。
- negative_prompt:生成图片的反关键词,让生成的图片不包含什么。
- default_negative_prompt:使用apispace提供的默认反关键词,避免出现低质量图片,和不完整肢体身体的动物和人物。1为使用,0为不使用,不填默认使用。
- sampler_name:图像生成的采样器选择,不同采样器会影响生成的图片的风格,构图,默认为Euler。
- steps:生成图片迭代次数,取值在1到50之间,越高图片越精细,默认为30,一般30次就足够了,迭代次数越大,生成图片时间越长。
- width:生成图片的宽度,默认为512,取值在50到1024之间。
- height:生成图片的高度,默认为512,取值在50到1024之间。
- model:选择生成图片的模型,有“通用”和“二次元”。
- cfg_scale:指导程度参数,设置越高生成的图片就会越接近prompt,越低会越脱离prompt但是会产生有创意的结果。取值范围1到20,默认为7,推荐5,7,12。
相关文章:

想要的古风女生头像让你快速get
如今我看到很多人都喜欢用古风女生当作头像,那么今天我就来教大家如何快速得到一张超美的古风女生头像~ 上图就是我使用 APISpace 的 AI作画(图像生成)服务 快速生成的古风女生头像,不仅可以限定颜色,还可以选择『宝石镶嵌』或『花卉造型』这…...

传统企业数字化转型,到底难在哪里?
数字化转型过程中面临最大的挑战和问题是什么?这篇整理了企业在数字化转型过程中普遍面临的9大问题和挑战以及如何解决这些问题,希望能够对各位企业数字化转型有多启发和帮助。 01 企业数字化转型三大现状 在梳理企业数字化转型问题之前,我想…...
)
Python:青蛙跳杯子(BFS)
题目描述 X 星球的流行宠物是青蛙,一般有两种颜色:白色和黑色。 X 星球的居民喜欢把它们放在一排茶杯里,这样可以观察它们跳来跳去。 如下图,有一排杯子,左边的一个是空着的,右边的杯子,每个…...

6.10 谱分解
文章目录计算方法代码实现计算方法 单纯矩阵normal matrix指的是符号ATAAATA^TAAA^TATAAAT的矩阵,他们的特征值互异。此外,单纯矩阵还有个特点,他们的特征空间彼此正交。 对于单纯矩阵,存在以下的谱定理Spectral theorem&…...

MySQL入门篇-MySQL 行转列小结
备注:测试数据库版本为MySQL 8.0 需求:求emp表各个岗位的工资之和,如无,用0代替 如需要scott用户下建表及录入数据语句,可参考:scott建表及录入数据sql脚本 CASE语法 SELECT deptno,ifnull(sum(case when job MANAGER then sal else 0 …...

项目管理常见的十大难题及其症状
01缺少维护文档时常,项目工作紧张时,第一个去掉的就是文档工作。有时即使项目有时间,也不会创建文档;或是创建了文档,却很少在项目进行过程中维护它。症状产品与需求文档不符;技术文档过时,无法保证技术的延…...

技术方案模板
0.基本原则 1.可量化,很大、很多、很高 到底是多少?基本没影响,到底有没有影响什么情况下有影响? 2.可实施,结合实际情况最终可落地 3.可指导,非方案制定人能理解,能在尽量少的人工沟通的情况下实现方案 4.可复用,设计的方案,再次出现类似需求时可以做到少开发或不…...

MySQL中对于单表和多表的操作
一、单表查询素材: 表名:worker-- 表中字段均为中文,比如 部门号 工资 职工号 参加工作 等显示所有职工的基本信息。mysql8.0 [chap03]>select * from worker;查询所有职工所属部门的部门号,不显示重复的部门号。mysql8.0 [cha…...

MFI认证
一、什么是MFI认证? 苹果MFI认证,是苹果公司(Apple Inc.)对其授权配件厂商生产的外置配件的一种使用许可,MFi认证是apple公司Made for iPhone/iPad/iPod的英文缩写。是指分别为连接iPhone/iPad/iPod而特别设计的电子配件。 [图片] 二、iOS外设连接的几种方式 [图片] 这…...

Vue中mixins的使用
文章目录mixins介绍mixins特点mixins介绍 Mixins:在引入组件之后与组件中的对象和方法进行合并,相当于扩展了父组件的对象与方法,可以理解为形成了一个新的组件。混入 (mixins):是一种分发 Vue 组件中可复用功能的非常灵活的方式…...
【PyQt】PyQt学习(一)框架介绍+环境搭建
简介 写在最前面的话 在决定学习、使用一个框架之前需要考量如下几点: 框架运行效果;框架应用范围;框架学习成本和迁移成本;实现自己所需功能的开发效率; 只有综合考量如上四个方面,才能更好地选择适合…...

浅谈前端设计模式:策略模式和状态模式的异同点
一、策略模式 策略模式是定义一系列的算法,把它们一个个封装起来, 并且使它们可相互替换。 而且策略模式是重构小能力,特别适合拆分“胖逻辑”。 这个定义乍一看会有点懵,不过通过下面的例子就能慢慢理解它的意思。 先来看一个真实场景 某次活动要做…...

线性杂双功能PEG试剂OPSS-PEG-Acid,OPSS-PEG-COOH,巯基吡啶聚乙二醇羧基
英文名称:OPSS-PEG-COOH,OPSS-PEG-Acid 中文名称:巯基吡啶-聚乙二醇-羧基 OPSS-PEG-COOH是一种具有OPSS和羧基的线性杂双功能PEG试剂。它是一种有用的带有PEG间隔基的交联剂。OPSS代表正吡啶基二硫化物或邻吡啶基二硫代,与硫醇、…...

开发微服务电商项目演示(四)
一,网关服务限流熔断降级第1步:启动sentinel-dashboard控制台和Nacos注册中心服务第2步:在网关服务中引入sentinel依赖<!-- sentinel --> <dependency><groupId>com.alibaba.cloud</groupId><artifactId>sprin…...
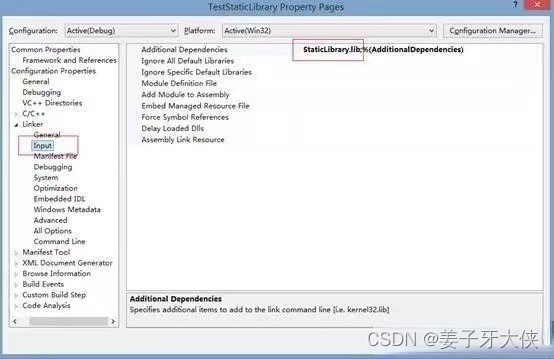
【C语言学习笔记】:静态库
一、什么是库 库是写好的现有的,成熟的,可以复用的代码。现实中每个程序都要依赖很多基础的底层库,不可能每个人的代码都从零开始,因此库的存在意义非同寻常。 本质上来说库是一种可执行代码的二进制形式,可以被操作…...

社科院与杜兰大学中外合作办学金融管理硕士——30+的年龄在职读研有必要吗?
说起读研,年龄在什么区间最合适呢?上次有位咨询的同学反馈年龄已经快35岁了,有一份不错的工作,但又不甘心止步于此,想要通过提升学历升职加薪,但又纠结自己是否能静下心来学习、是否能顺利毕业、拿到的证书…...
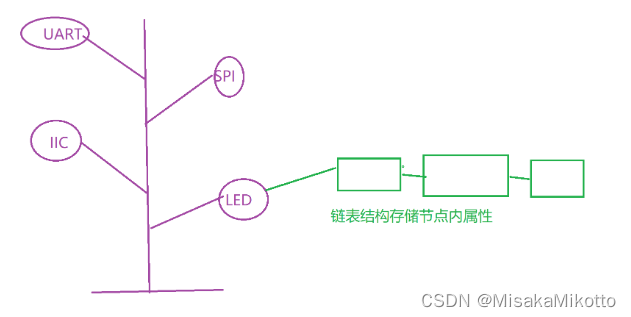
2.13作业【设备树解析,按自己理解】
设备树定义 设备树(device tree是描述硬件信息的一种树形结构,设备书文件在linux内核启动后被内核解析。描述一个硬件设备信息的节点我们叫做设备节点,一个设备节点内部包含当前硬件的多个不同属性,相同节点不同属性是以链式结构存…...

《NFL星计划》:巴尔的摩乌鸦·橄榄1号位
巴尔的摩乌鸦(英语:Baltimore Ravens)是一支职业美式橄榄球球队位于马里兰州的巴尔的摩。他们现时为美国美式橄榄球联合会的北区进行比赛,其主场为M&T银行体育场。乌鸦队曾在2000年和2012年取得超级碗冠军。 巴尔的摩乌鸦 成…...
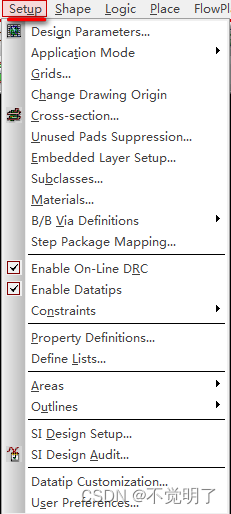
Allegro如何设置自动保存和自动保存的时间操作指导
Allegro如何设置自动保存和自动保存的时间操作指导 做PCB设计的时候,自动保存软件是一个必要的功能,Allegro同样支持设置自动保存,而且可以设置自动保存的时间。 如下图 具体操作如下 点击Setup点击User Preferences...
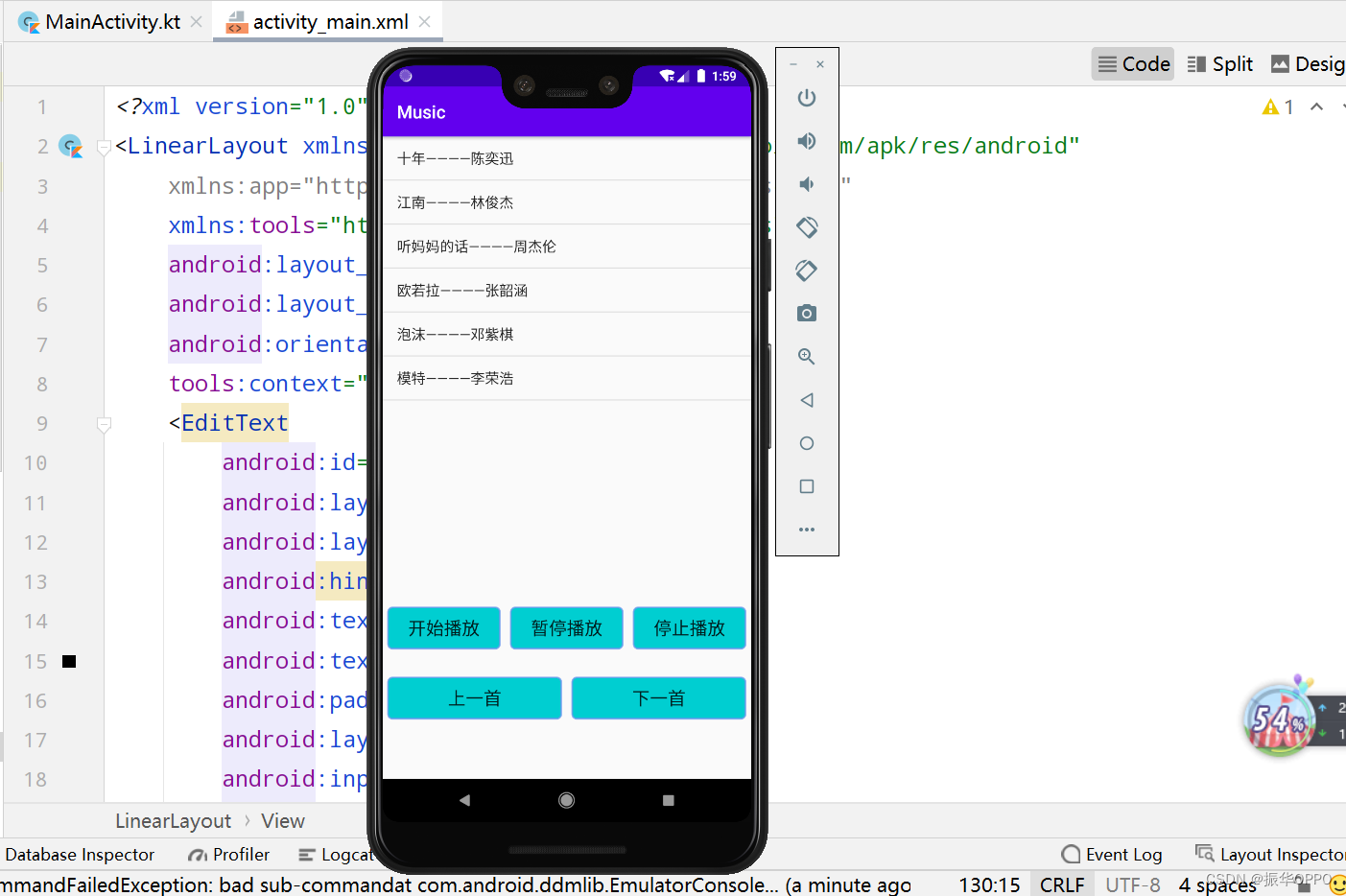
Kotlin实现简单音乐播放器
关于音乐播放器,我真的是接触比较多,听歌作为我第一大爱好,之前也用Java设计过音乐播放器,感兴趣的同学可以阅读:Android Studio如何实现音乐播放器(简单易上手)和 Android Studio实现音乐播放器…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

掌握 HTTP 请求:理解 cURL GET 语法
cURL 是一个强大的命令行工具,用于发送 HTTP 请求和与 Web 服务器交互。在 Web 开发和测试中,cURL 经常用于发送 GET 请求来获取服务器资源。本文将详细介绍 cURL GET 请求的语法和使用方法。 一、cURL 基本概念 cURL 是 "Client URL" 的缩写…...
