Tensorflow的数学基础
Tensorflow的数学基础
在构建一个基本的TensorFlow程序之前,关键是要掌握TensorFlow所需的数学思想。任何机器学习算法的核心都被认为是数学。某种机器学习算法的策略或解决方案是借助于关键的数学原理建立的。让我们深入了解一下TensorFlow的数学基础。
Scalar
标量是一个没有方向的物理量,完全由其大小来表征。标量是只有一维的向量。
# importing packages
import tensorflow as tf# creating a scalar
scalar = tf.constant(7)
scalar
输出:
<tf.Tensor: shape=(), dtype=int32, numpy=7>
检查尺寸:
scalar.ndim
输出:
0
Vector
矢量是一个有大小和方向的二维对象。我们可以把矢量从几何上解释为一个有方向的线段,箭头显示方向,线的长度等于矢量的大小。下面是一个在TensorFlow中创建矢量的例子。
# importing packages
import tensorflow as tf# create a vector
vector = tf.constant([10, 10])# checking the dimensions of vector
vector.ndim
输出:
1
Matrix
矩阵是一个术语,指的是以行和列组织的多维数组。行和列的长度决定了矩阵的大小。当一个矩阵有 “a “行和 “b “列时,该矩阵被表示为 “a*b “矩阵,这也指定了该矩阵的长度。
# importing packages
import tensorflow as tf# creating a matrix
matrix = tf.constant([[1, 2], [3, 4]])
print(matrix)
print('the number of dimensions of a matrix is :\
'+str(matrix.ndim))
输出:
tf.Tensor(
[[1 2][3 4]], shape=(2, 2), dtype=int32)
the number of dimensions of a matrix is : 2
数学操作
加法
当两个或多个矩阵具有相同的维度时,它们可以被加在一起。术语 “加法 “指的是将每个元素添加到给定的位置或地点的过程。
# importing packages
import tensorflow as tf# creating two tensors
matrix = tf.constant([[1, 2], [3, 4]])
matrix1 = tf.constant([[2, 4], [6, 8]])# addition of two matrices
print(matrix+matrix1)
输出:
tf.Tensor(
[[ 3 6][ 9 12]], shape=(2, 2), dtype=int32)
减法
矩阵的减法与两个矩阵的加法的工作方式相同。如果两个矩阵的尺寸相同,用户可以将它们相减。
# importing packages
import tensorflow as tf# creating two tensors
matrix = tf.constant([[1, 2], [3, 4]])
matrix1 = tf.constant([[2, 4], [6, 8]])# subtraction of two matrices
print(matrix1 - matrix)
输出:
tf.Tensor(
[[1 2][3 4]], shape=(2, 2), dtype=int32)
乘法
维度n必须等于a,两个矩阵m*n和a*b才可以相乘。m*b是结果矩阵。
# importing packages
import tensorflow as tf# creating two tensors
matrix = tf.constant([[1, 2], [3, 4]])
matrix1 = tf.constant([[2, 4], [6, 8]])# multiplication of two matrices
print(matrix1 * matrix)
输出:
tf.Tensor(
[[ 2 8][18 32]], shape=(2, 2), dtype=int32)
除法
为了执行除法,两个矩阵必须具有相同的维度,就像加法一样。
# importing packages
import tensorflow as tf# creating two tensors
matrix = tf.constant([[1, 2],[3, 4]])
matrix1 = tf.constant([[2, 4],[6, 8]])# division of two matrices
print(matrix1 / matrix)
输出:
tf.Tensor(
[[2. 2.][2. 2.]], shape=(2, 2), dtype=float64)
矩阵的转置
矩阵的转置是通过将其行转换成列或将列转换成行来确定的。所提供的矩阵上标中的字母 “T “表示该矩阵的转置。
矩阵M m_n的转置是MT(转置)n_m,它是通过将列向量转置为行向量而得到的。Tf.transpose()方法用于在TensorFlow中查找矩阵的转置。如果M是一个矩阵,转置用M T表示
# importing packages
import tensorflow as tf# creating a matrix
matrix = tf.constant([[1, 2], [3, 4]])
# transpose of the matrix
print(tf.transpose(matrix))
输出:
tf.Tensor(
[[1 3][2 4]], shape=(2, 2), dtype=int32)
点积
匹配成分的乘积之和是两个向量的点积。在同一轴上的成分,可以表示为:
tf.tensodot()方法用于在TensorFlow中寻找点积。当我们指定轴=1时,矩阵乘法就会发生。
# importing packages
import tensorflow as tf# creating a matrix
matrix = tf.constant([[1, 2], [3, 4]])# dot product of matrices
print('dot product of matrices is : ' +str(tf.tensordot(matrix, matrix, axes=1)))
输出:
dot product of matrices is : tf.Tensor(
[[ 7 10][15 22]], shape=(2, 2), dtype=int32)
相关文章:

Tensorflow的数学基础
Tensorflow的数学基础 在构建一个基本的TensorFlow程序之前,关键是要掌握TensorFlow所需的数学思想。任何机器学习算法的核心都被认为是数学。某种机器学习算法的策略或解决方案是借助于关键的数学原理建立的。让我们深入了解一下TensorFlow的数学基础。 Scalar 标…...

IT培训就是“包就业”吗?内行人这么看
大部分人毕业后选择参加职业技能培训,都是为了学完之后能找到好工作,而“就业服务”也成为各家培训机构对外宣传的重点内容。那么,所谓的“就业服务”就是“包就业”和“包底薪”吗?学完就一定能拿到offer吗?今天&…...

【算法】【数组与矩阵模块】顺时针旋转打印矩阵
目录前言问题介绍解决方案代码编写java语言版本c语言版本c语言版本思考感悟写在最后前言 当前所有算法都使用测试用例运行过,但是不保证100%的测试用例,如果存在问题务必联系批评指正~ 在此感谢左大神让我对算法有了新的感悟认识! 问题介绍 …...

Java中的锁概述
java中的锁java添加锁的两种方式:synchronized:关键字 修饰代码块,方法 自动获取锁、自动释放锁Reentrantlock:类 只能修饰代码块 手动加锁、释放锁java中锁的名词一些锁的名词指的是锁的特性,设计,状态&am…...

微电影行业痛点解决方案
在当下新媒体时代,微电影作为“微文化”的载体,具有“微”的特点,经过短短数年的快速发展,并获得了受众广泛的关注和喜爱,对人们的休闲娱乐方式也产生较大的影响。但在迅猛发展的同时也存在一些行业痛点,诸…...
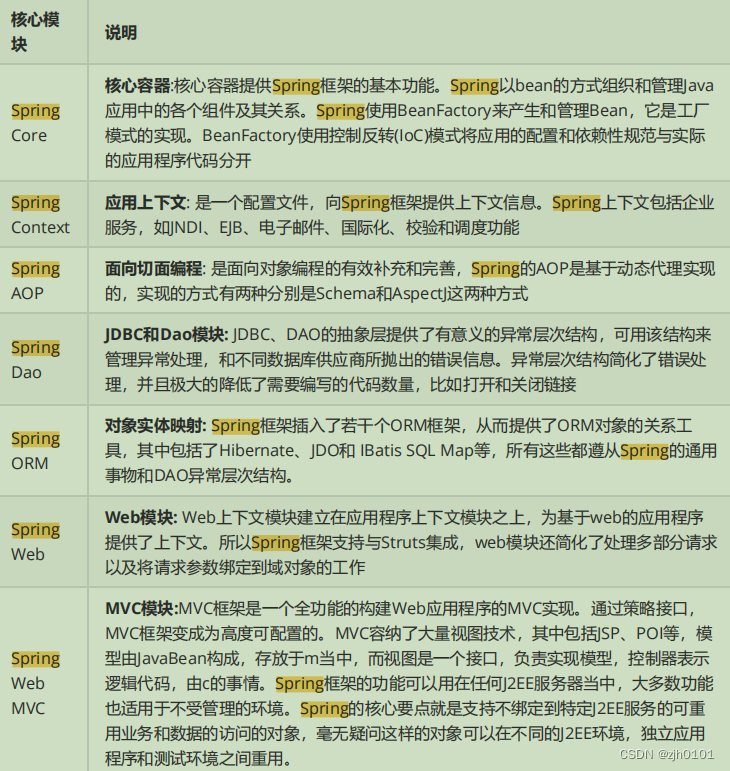
使用Spring框架的好处是什么
使用Spring框架的好处是什么? 1、轻量:Spring 是轻量的,基本的版本大约2MB。 2、控制反转:Spring通过控制反转实现了松散耦合,对象们给出它们的依赖,而不是创建或查找依赖的对象们。 3、面向切面的编程(AOP…...
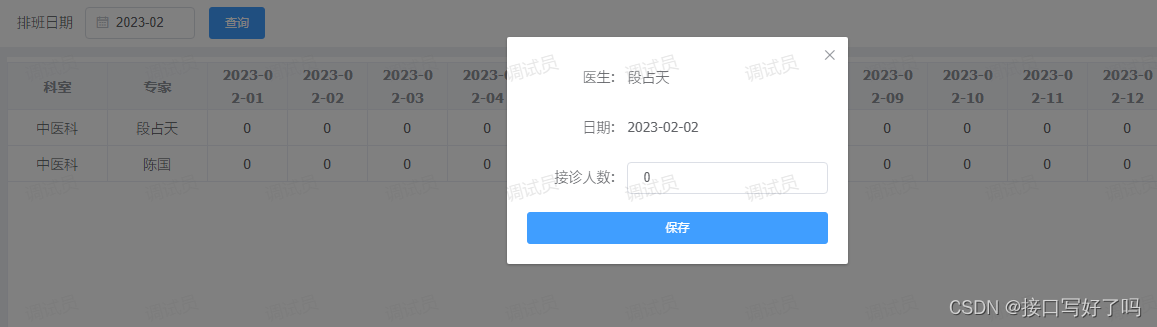
【表格单元格可编辑】vue-elementul简单实现table表格点击单元格可编辑,点击单元格变成弹框修改数据
前言 这是继我另一个帖子就是单元格点击变成输入框后添加的功能 因为考虑到有些时候修改单元格的信息可能点击后要修改很多,那一个输入框不好用 所以这时候就需要一个弹框可以把所有表单都显示出来修改 所以这里就专门又写了一个demo,用于处理这种情况 …...

vue3.0 响应式数据
目录1.什么是响应式2. 选项式 API 的响应式数据3.组合式 API 的响应式数据3.1 reactive() 函数3.2 toref() 函数3.3 toRefs() 函数3.4ref() 函数总结1.什么是响应式 这个术语在今天的各种编程讨论中经常出现,但人们说它的时候究竟是想表达什么意思呢?本质…...

uni-app ①
文章目录一、uni-app简介学习 uniapp 本质uniapp 优势uni-app 和 vue 的关系uni-app 和小程序有什么关系uniapp 与 web 代码编写区别课程内容学习重点知识点一、uni-app 简介 uni-app 是一个使用 Vue.js 进行 开发所有前端应用的框架。开发者编写一套代码,即可发布…...

20个 Git 命令玩转版本控制
想要在团队中处理代码时有效协作并跟踪更改,版本控制发挥着至关重要的作用。Git 是一个版本控制系统,可以帮助开发人员跟踪修订、识别文件版本,并在必要的时候恢复旧版本。Git 对于有一定编程经验的用户来说虽然不算太难,但是想要…...
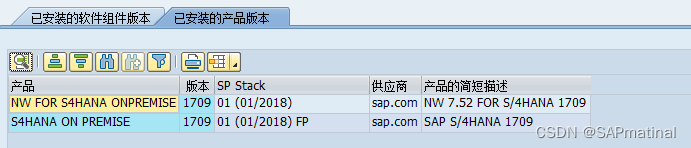
SAP NetWeaver版本和SAP Kernel版本的确定
SAP NetWeaver(SAP NW)描述了用于“业务启用”的所有软件和服务。SAP业务套件(如ERP中央组件(ECC)或供应商关系管理(SRM))包含该特定业务解决方案的软件组件。 以下是SAP NetWeaver…...
面试23K字节测试开发岗被血虐,到底具有怎样的技术才算高级水平?
前几天我朋友跟我吐苦水,这波面试又把他打击到了,做了6年软件测试。。。 下面这条招聘是在腾讯招聘官网截图下来的,首先我们对高级水平下一个定义吧,那它应该是对标这个职级该有的能力 什么样的工程师才能算高级?至少…...

智云通CRM:买对了吗——大客户采购的方案实施
一旦采购合同签署后,供应商就要履行合同,按时交付产品进场使用,或实施服务方案。不过,无论对供应商还是客户来说,双方的合作并没有就此结束。 在这个阶段,客户会评估此次合作的供应商做事是否靠谱&#x…...
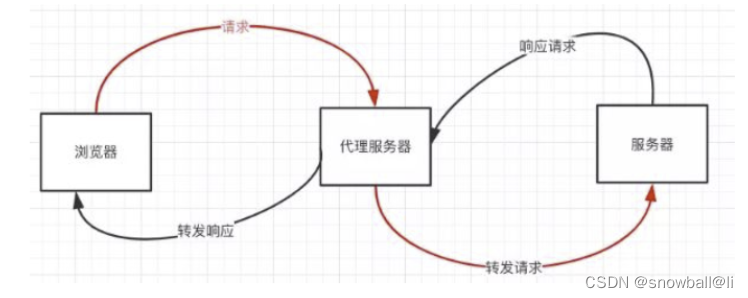
前后端开发过程中的跨域问题总结
1.何为跨域问题 出于浏览器的同源策略限制。同源策略是一种约定,它是浏览器最核心也最基本的安全功能,如果缺少了同源策略,则浏览器的正常功能不能使用。可以说web是构建在同源策略基础之上的,浏览器只是针对同源策略的一种实现。…...
爬虫:栖落的电影网站,利用requests和re模块
这是栖落的电影网站地址:https://xxx.xxx 进入网页,显示: 爬取目标:电影的名称、观影人数和评分。 易知本网站的url url "https://xxx.xxx" 本网站会识别出headers中的python请求而拒绝访问,所以需要更改…...

使用burpsuite抓包 + sql工具注入 dvwa靶场
使用burpsuite抓包 sql工具注入 dvwa靶场 记录一下自己重新开始学习web安全之路②。 一、准备工作 1.工具准备 sqlmap burpsuite 2.浏览器准备 火狐浏览器 设置代理。 首先,先设置一下火狐浏览器的代理 http代理地址为127.0.0.0.1 ,端口为8080 …...
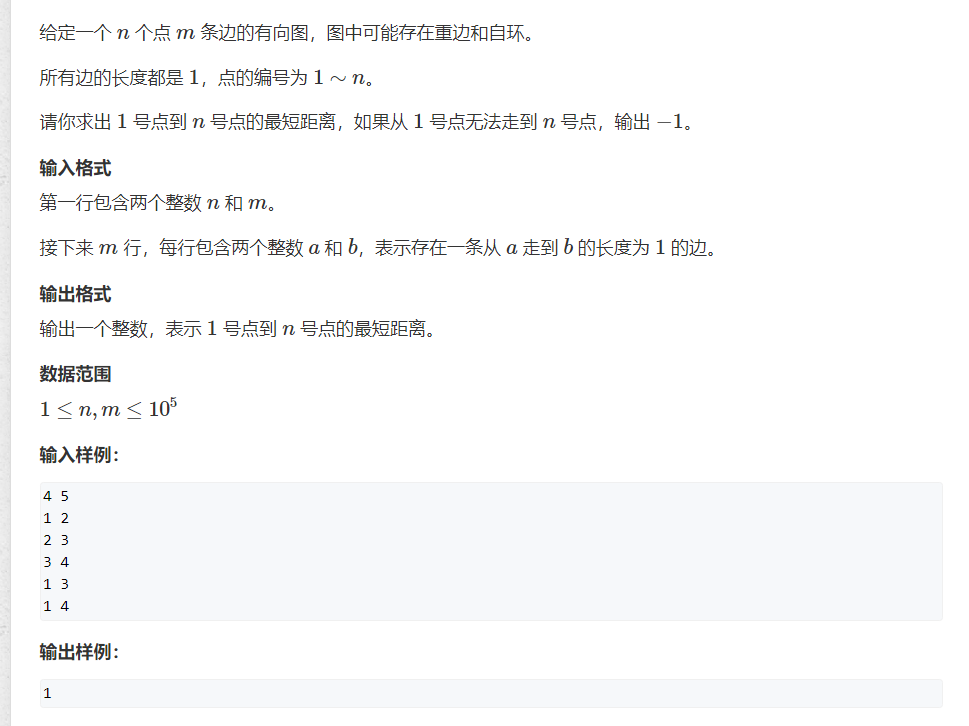
树与图中的dfs和bfs—— AcWing 846. 树的重心 AcWing 847. 图中点的层次
一、AcWing 846. 树的重心1.1题目1.2思路分析题意:什么是树的重心?树的重心是指,删除某个结点后剩下的最大连通子树的结点数目最小,如下图是根据样列生成的树,若删除结点1,则剩下三个子树最大的是中间那颗结…...

从零开始学数据分析之数据分析概述
当今世界对信息技术的依赖程度在不断加深,每天都会有大量的数据产生,我们经常会感到数据越来越多,但是要从中发现有价值的信息却越来越难。 这里所说的信息,可以理解为对数据集处理之后的结果,是从数据集中提炼出的可…...

十五载厚积薄发,电信级分布式数据库是这样炼成
所在论坛:数据库技术创新&云原生论坛 分享时段:2.18 10:00-10:30 分享主题:大规模并行处理:AntDB分布式演进之路 分享嘉宾:沈夺,亚信科技AntDB数据库内核开发工程师 由中国开源软件推进联盟Postgre…...

Centos调整分区存储大小
将/home下900G转移到/目录下 1、查看分区大小:df -hl 2、备份home文件:tar cvf /run/home.tar /home 3、终止home文件进程(切换到非home路径下执行这个命令):fuser -km /home 3.1、如果没有fuser,在线安装…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...

解析“道作为序位生成器”的核心原理
解析“道作为序位生成器”的核心原理 以下完整展开道函数的零点调控机制,重点解析"道作为序位生成器"的核心原理与实现框架: 一、道函数的零点调控机制 1. 道作为序位生成器 道在认知坐标系$(x_{\text{物}}, y_{\text{意}}, z_{\text{文}}…...
