【taichi】利用 taichi 编写深度学习算子 —— 以提取右上三角阵为例
本文以取 (bs, n, n) 张量的右上三角阵并展平为向量 (bs, n*(n+1)//2)) 为例,展示如何用 taichi 编写深度学习算子。
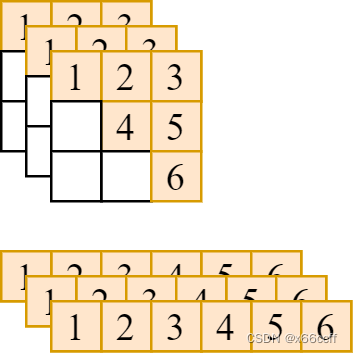
如图,要把形状为 (bs,n,n)(bs,n,n)(bs,n,n) 的张量,转化为 (bs,n(n+1)2)(bs,\frac{n(n+1)}{2})(bs,2n(n+1)) 的向量。我们先写一个最简单的最慢的纯 python 循环实现方法
纯 python for 循环
def get_tensor_up_right_tri_slow(t):# t shape (bs, n, n)# out shape (bs, n*(n+1)//2)out = torch.zeros(t.shape[0], t.shape[1]*(t.shape[1]+1)//2)n = t.shape[1]# k = i*n + j - i*(i+1)//2for b in range(t.shape[0]):# 遍历右上三角阵,包括主对角线for i in range(t.shape[1]):for j in range(i, t.shape[1]):k = i*n + j - i*(i+1)//2out[b, k] = t[b, i, j]return out
可想而知,三层 python for 循环,必然是极慢的了。
转化为 taichi
在此基础上,稍微做一些修改,就可以得到我们的 taichi 版本函数
import taichi as titi.init(arch=ti.gpu)@ti.kernel
def get_tensor_up_right_tri(t: ti.types.ndarray(ndim=3, dtype=ti.f32), out: ti.types.ndarray(ndim=2, dtype=ti.f32)):# t shape (bs, n, n)# out shape (bs, n*(n+1)//2)n = t.shape[1]for b, i, j in t:# 遍历右上三角阵,包括主对角线if i <= j:k = i*n + j - i*(i+1)//2out[b, k] = t[b, i, j]
taichi 支持同时遍历多层循环,将三层循环改为一层循环后,和 python for 循环版本基本没有什么差别。taichi 将此函数转化为 CUDA 版本进行加速,从而提高运算速度。
相关文章:

【taichi】利用 taichi 编写深度学习算子 —— 以提取右上三角阵为例
本文以取 (bs, n, n) 张量的右上三角阵并展平为向量 (bs, n*(n1)//2)) 为例,展示如何用 taichi 编写深度学习算子。 如图,要把形状为 (bs,n,n)(bs,n,n)(bs,n,n) 的张量,转化为 (bs,n(n1)2)(bs,\frac{n(n1)}{2})(bs,2n(n1)) 的向量。我们先写…...

二进制 k8s 集群下线 worker 组件流程分析和实践
文章目录[toc]事出因果个人思路准备实践当前 worker 节点信息将节点标记为不可调度驱逐节点 pod将 worker 节点从 k8s 集群踢出下线 worker 节点相关组件事出因果 因为之前写了一篇 二进制 k8s 集群下线 master 组件流程分析和实践,所以索性再写一个 worker 节点的缩…...

Bean的六种作用域
限定程序中变量的可用范围叫做作用域,Bean对象的作用域是指Bean对象在Spring整个框架中的某种行为模式~~ Bean对象的六种作用域: singleton:单例作用域(默认) prototype:原型作用域(多例作用域…...

Http发展历史
1 缘起 有一次,听到有人在议论招聘面试的人员, 谈及应聘人员的知识深度,说:问了一些关于Http的问题,如Http相关结构、网络结构等, 然后又说,问没问相关原理、来源? 我也是有些困惑了…...

高级Java程序员必备的技术点,你会了吗?
很多程序员在入行之后的前一两年,快速学习到了做项目常用的各种技术之后,便进入了技术很难寸进的平台期。反正手里掌握的一些技术对于应付普通项目来说,足够用了。因此也会缺入停滞,最终随着年龄的增长,竞争力不断下降…...

【暴力量化】查找最优均线
搜索逻辑 代码主要以支撑概率和压力概率来判断均线的优劣 判断为压力: 当日线与测试均线发生金叉或即将发生金叉后继续下行 判断为支撑: 当日线与测试均线发生死叉或即将发生死叉后继续上行 判断结果的天数: 小于6日均线,用金叉或…...
Java读取mysql导入的文件时中文字段出现�??的乱码如何解决
今天在写程序时遇到了一个乱码问题,困扰了好久,事情是这样的, 在Mapper层编写了查询语句,然后服务处调用,结果控制器返回一堆乱码 然后查看数据源头处: 由重新更改解码的字符集,在数据库中是正…...
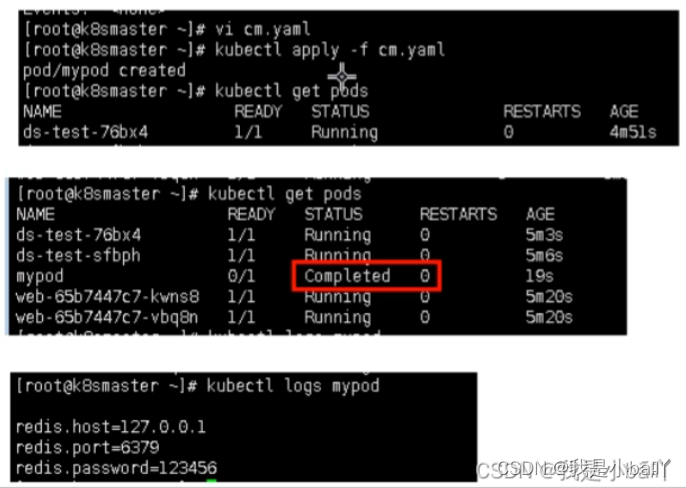
k8s核心概念—Pod Controller Service介绍——20230213
文章目录一、Pod1. pod概述2. pod存在意义3. Pod实现机制4. pod镜像拉取策略5. pod资源限制6. pod重启机制7. pod健康检查8. 创建pod流程9. pod调度二、Controller1. 什么是Controller2. Pod和Controller关系3. deployment应用场景4. 使用deployment部署应用(yaml&a…...

Tensorflow的数学基础
Tensorflow的数学基础 在构建一个基本的TensorFlow程序之前,关键是要掌握TensorFlow所需的数学思想。任何机器学习算法的核心都被认为是数学。某种机器学习算法的策略或解决方案是借助于关键的数学原理建立的。让我们深入了解一下TensorFlow的数学基础。 Scalar 标…...

IT培训就是“包就业”吗?内行人这么看
大部分人毕业后选择参加职业技能培训,都是为了学完之后能找到好工作,而“就业服务”也成为各家培训机构对外宣传的重点内容。那么,所谓的“就业服务”就是“包就业”和“包底薪”吗?学完就一定能拿到offer吗?今天&…...

【算法】【数组与矩阵模块】顺时针旋转打印矩阵
目录前言问题介绍解决方案代码编写java语言版本c语言版本c语言版本思考感悟写在最后前言 当前所有算法都使用测试用例运行过,但是不保证100%的测试用例,如果存在问题务必联系批评指正~ 在此感谢左大神让我对算法有了新的感悟认识! 问题介绍 …...

Java中的锁概述
java中的锁java添加锁的两种方式:synchronized:关键字 修饰代码块,方法 自动获取锁、自动释放锁Reentrantlock:类 只能修饰代码块 手动加锁、释放锁java中锁的名词一些锁的名词指的是锁的特性,设计,状态&am…...

微电影行业痛点解决方案
在当下新媒体时代,微电影作为“微文化”的载体,具有“微”的特点,经过短短数年的快速发展,并获得了受众广泛的关注和喜爱,对人们的休闲娱乐方式也产生较大的影响。但在迅猛发展的同时也存在一些行业痛点,诸…...
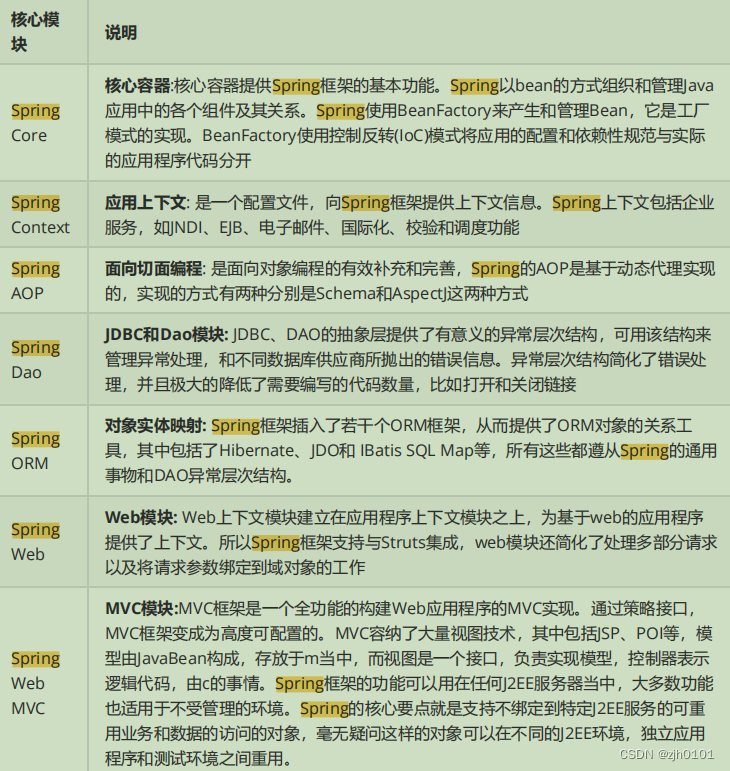
使用Spring框架的好处是什么
使用Spring框架的好处是什么? 1、轻量:Spring 是轻量的,基本的版本大约2MB。 2、控制反转:Spring通过控制反转实现了松散耦合,对象们给出它们的依赖,而不是创建或查找依赖的对象们。 3、面向切面的编程(AOP…...
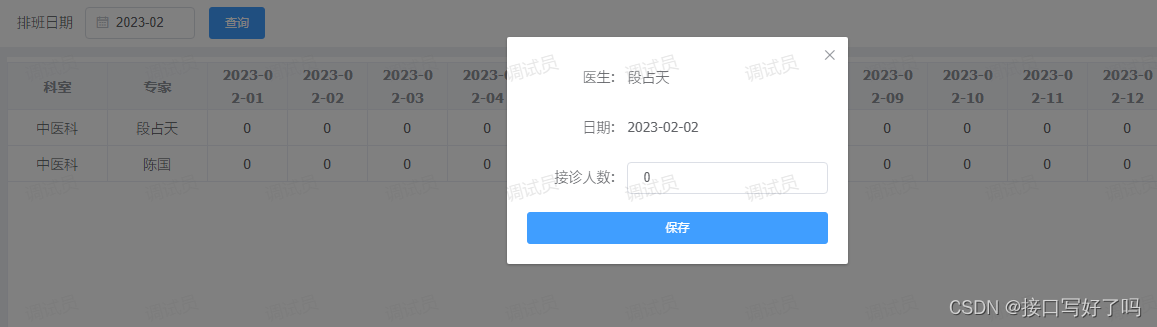
【表格单元格可编辑】vue-elementul简单实现table表格点击单元格可编辑,点击单元格变成弹框修改数据
前言 这是继我另一个帖子就是单元格点击变成输入框后添加的功能 因为考虑到有些时候修改单元格的信息可能点击后要修改很多,那一个输入框不好用 所以这时候就需要一个弹框可以把所有表单都显示出来修改 所以这里就专门又写了一个demo,用于处理这种情况 …...

vue3.0 响应式数据
目录1.什么是响应式2. 选项式 API 的响应式数据3.组合式 API 的响应式数据3.1 reactive() 函数3.2 toref() 函数3.3 toRefs() 函数3.4ref() 函数总结1.什么是响应式 这个术语在今天的各种编程讨论中经常出现,但人们说它的时候究竟是想表达什么意思呢?本质…...

uni-app ①
文章目录一、uni-app简介学习 uniapp 本质uniapp 优势uni-app 和 vue 的关系uni-app 和小程序有什么关系uniapp 与 web 代码编写区别课程内容学习重点知识点一、uni-app 简介 uni-app 是一个使用 Vue.js 进行 开发所有前端应用的框架。开发者编写一套代码,即可发布…...

20个 Git 命令玩转版本控制
想要在团队中处理代码时有效协作并跟踪更改,版本控制发挥着至关重要的作用。Git 是一个版本控制系统,可以帮助开发人员跟踪修订、识别文件版本,并在必要的时候恢复旧版本。Git 对于有一定编程经验的用户来说虽然不算太难,但是想要…...
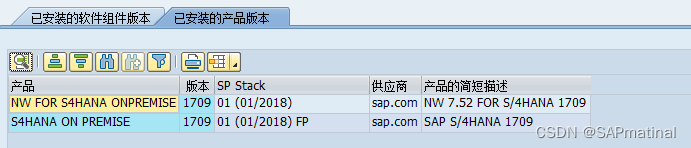
SAP NetWeaver版本和SAP Kernel版本的确定
SAP NetWeaver(SAP NW)描述了用于“业务启用”的所有软件和服务。SAP业务套件(如ERP中央组件(ECC)或供应商关系管理(SRM))包含该特定业务解决方案的软件组件。 以下是SAP NetWeaver…...
面试23K字节测试开发岗被血虐,到底具有怎样的技术才算高级水平?
前几天我朋友跟我吐苦水,这波面试又把他打击到了,做了6年软件测试。。。 下面这条招聘是在腾讯招聘官网截图下来的,首先我们对高级水平下一个定义吧,那它应该是对标这个职级该有的能力 什么样的工程师才能算高级?至少…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...
