模型解释性:SHAP包的使用
本篇博客介绍另一种事后可解释性方法:SHAP(SHapley Additive exPlanation)方法。
1. Shapley值理论
Shapley值是博弈论中的一个概念,通过衡量联盟中各成员对联盟总目标的贡献程度,从而根据贡献程度来进行联盟成员的利益分配,避免了分配的平均主义。
当Shapley理论用于解释机器学习模型的时候,将输入特征xxx视为参与成员,模型输出的概率分布f(x)f(x)f(x)视为联盟总目标,通过衡量各特征的贡献度来挖掘重要特征,从而提供可解释性判断依据。其数学模型如下:g(Z′)=φ0+∑j=1MφjZj′≈f(x)(1)g(Z^{'})=\varphi_{0}+\sum_{j=1}^{M}\varphi_{j}Z^{'}_{j}\approx f(x) \tag{1}g(Z′)=φ0+j=1∑MφjZj′≈f(x)(1)其中,ggg是解释模型,f(x)f(x)f(x)是原机器学习模型,Zj′={0,1}MZ^{'}_{j}=\{0,1\}^{M}Zj′={0,1}M表示相应特征是否被观察到,MMM是输入特征的数目,φi\varphi_{i}φi是每个特征的归因值,φ0\varphi_{0}φ0是解释模型的常数。
对于一个特定的输入数据x0x_{0}x0,其Shapley值的计算公式如下:φi(f,x0)=∑S⊆NS/{i}∣S∣!(M−∣S∣−1)!∣NS∣\varphi_{i}(f,x_{0})=\sum_{S\subseteq N_{S}/ \{i\}}\frac{|S|!(M-|S|-1)!}{|N_{S}|!}[f(S\cup\{i\})-f(S)]\tag{2}φi(f,x0)=S⊆NS/{i}∑∣NS∣!∣S∣!(M−∣S∣−1)其中,φi(f)\varphi_{i}(f)φi(f)代表函数fff中特征iii的贡献度,NSN_{S}NS是所有特征组成的集合,SSS代表特征子集,NS/{i}N_{S}/\{i\}NS/{i}代表在集合NSN_{S}NS中去除特征iii,S∪{i}S\cup \{i\}S∪{i}表示子集SSS中增加特征iii,∣S∣|S|∣S∣表示集合SSS中元素的个数。
为了方面公式(2)的计算,通常将公式(2)转化为如下公式计算:φi(f,x0)=∑z′∈{0,1}M∣z′∣!(M−∣z′∣−1)!M\varphi_{i}(f,x_{0})=\sum_{z^{'}\in\{0,1\}^{M}}\frac{|z^{'}|!(M-|z^{'}|-1)!}{M!}[f_{S}(z^{'})-f_{S}(z^{'}|i)]\tag{3}φi(f,x0)=z′∈{0,1}M∑M!∣z′∣!(M−∣z′∣−1)其中,fS=E[f(x)∣zS′]=1N∑j=1Nf(xj′)f_{S}=E[f(x)|z_{S}^{'}]=\frac{1}{N}\sum_{j=1}^{N}f(x_{j}^{'})fS=E[f(x)∣zS′]=N1j=1∑Nf(xj′)其中,zS′z_{S}^{'}zS′为集合SSS中特征的取值所组成的集合,NNN为原函数fff训练数据的个数,xj′x_{j}^{'}xj′的取值如下:xj′={x0i,Fi∈zS′xji,Fi∉zS′x_{j}^{'}=\left\{\begin{aligned} x_{0i},& F_{i}\in z_{S}^{'} \\ x_{ji},&F_{i}\notin z_{S}^{'} \end{aligned}\right. xj′={x0i,xji,Fi∈zS′Fi∈/zS′其中,x0ix_{0i}x0i为待解释数据x0x_{0}x0的第iii个特征值,xjix_{ji}xji表示第jjj个训练数据中第iii个特征的取值,FiF_{i}Fi表示第iii个特征值。
SHAP值具备扎实的理论基础,但φi\varphi_{i}φi的计算复杂度和E[f(x)∣zS′]E[f(x)|z_{S}^{'}]E[f(x)∣zS′]的有效估计是其在实际应用中的最大阻碍,为了解决这个问题,Lundberg等人提出了Tree SHAP方法。
Tree SHAP是用于树模型的快速SHAP值估计方法,大大增加了SHAP值的实际应用能力。
2 SHAP包用法
这里仍然以Boston房价为例,使用XGBoost方法训练模型。其用法举例如下:
模型训练
import pandas as pd
import numpy as np
from sklearn.datasets import load_boston
from xgboost import XGBRegressor
from sklearn.model_selection import train_test_split
import shap
shap.initjs()
#分类
boston=load_boston()
X=boston.data
y=boston.target
features=boston.feature_names
X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.2,random_state=0)xgbr=XGBRegressor(n_estimators=200,max_depth=4)
xgbr.fit(X_train,y_train)
对单个样本进行解释
explainer=shap.TreeExplainer(xgbr)
shap_values=explainer.shap_values(X_test[1].reshape(1,-1))
shap.force_plot(explainer.expected_value,shap_values,X_test[1].reshape(1,-1),feature_names=features)
其结果如下:

关于上图,有以下几个方面需要说明:
- base_value:全体样本Shape平均值,这里的全体样本指的是模型的训练样本;
- output_value: 当前样本的Shap输出值,即为模型的预测值;
- 正向作用特征:红色特征即为正向作用的特征;
- 反向作用特征:蓝色特征即为反向作用的特征;
整个测试集的Shap分布
explainer=shap.TreeExplainer(xgbr)
shap_values=explainer.shap_values(X_test)
shap.force_plot(explainer.expected_value,shap_values,X_test,feature_names=features)
其结果如下(可以通过调节横纵坐标观察当个特征的效果):

从特征角度观察样本Shap值
shap.summary_plot(shap_values,X_test,feature_names=features)
其结果如下:

参考文献
- 《基于图模型机器学习算法的可解释性技术研究与实现》
- 《稳定评估机器学习模型可解释性研究》
- https://blog.csdn.net/tMb8Z9Vdm66wH68VX1/article/details/106131890
相关文章:

模型解释性:SHAP包的使用
本篇博客介绍另一种事后可解释性方法:SHAP(SHapley Additive exPlanation)方法。 1. Shapley值理论 Shapley值是博弈论中的一个概念,通过衡量联盟中各成员对联盟总目标的贡献程度,从而根据贡献程度来进行联盟成员的利益分配,避免…...

算法训练营 day45 动态规划 0-1背包理论 分割等和子集
算法训练营 day45 动态规划 0-1背包理论 分割等和子集 0-1背包理论 有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。 在下面的讲解中&…...

SSM框架
1.mybatis的底层原理 本质上就是使用反射和动态代理来实现对应的映射关系 2.日志级别 3.传递参数 单个参数的传递和多个参数的传递 Emp selectOne(Param(“xingming”) String name); List selectByCondition(Param(“name”) String name,Param(“sal”) double sal); 4.#和…...

教育行业需要什么样的客服系统?
某教育公司拥有素质教育、成人教育、智慧教育等多个业务板块,日常通过电商、线上媒体、线上线下授课等方式进行业务开展和品牌宣传,取得了非常不错的成绩,受到了很多人的好评反馈。 对于这样一个教育公司,客户来源广泛࿰…...

花房集团任命新首席财务官:已跌破IPO发行价,活跃用户下滑
上市刚满2个月,花椒母公司花房集团(HK:03611)的高管就发生了变更。2023年2月12日,花房集团披露的公告显示,董事会宣布赵磊为该公司首席财务官(CFO),自2023年2月10日起生效。 据贝多…...

儿童绘本馆图书借阅租赁知识付费小程序源码交流
1.分类图书 2.书单推荐 4.会员卡次、期限购买 5.借阅时间选择 6.积分签到 7.优惠Q领取 前端uniapp开发 后端thinkphp开发 完全开源 <template> <view class"sp-section sp-index"> <!-- search --> <view class&qu…...

Vue3 中 axios 的安装及使用
目录前言:一、什么是 axios ?二、Axios 的配置项三、Axios 的请求方式四、自定义创建实例五、Axios 请求错误处理六、Axios 解决跨域问题七、Axios 请求案例随机笑话大全总结:前言: 在编写vue里的项目时,必须要用和后台…...

Django设计模式以及模板层介绍
MVC和MTV 传统的MVC作用:降低模块间的耦合度(解耦)Django的MTV模式 作用:降低模块间的耦合度(解耦)什么是模板 1、模板是可以根据字典数据动态变化的html网页2、模板可以根据视图中传递的字典数据动态生成相…...

Linux信号一门搞定
1.信号是什么? 信号其实就是一个软件中断。 例: 输入命令,在Shell下启动一个前台进程。用户按下Ctrl-C,键盘输入产生一个硬件中断。如果CPU当前正在执行这个进程的代码,则该进程的用户空间代码暂停执行,…...

手撸一个动态Feign,实现一个“万能”接口调用
Feign,在微服务框架中,是的服务直接的调用变得很简洁、简单,而不需要再编写Java Http调用其他微服务的接口。 动态feign 对于fegin调用,我们一般的用法:为每个微服务都创建对应的feignclient接口,然后为每…...
Linux Capabilities 入门
目录 Linux capabilities 是什么? capabilities 的赋予和继承 线程的 capabilities Permitted Effective Inheritable Bounding Ambient 文件的 capabilities Permitted Inheritable Effective 运行 execve() 后 capabilities 的变化 案例 Linux capab…...

驱动 day6
关于设备树的理解: 设备树(Device Tree)是一种用于特定硬件设备的解释语法树。它用来表示存储有关主板硬件和CPU架构信息的数据在内核中的传递格式,使内核可以更好地了解硬件并支持它们,而不必编写固定的代码。设备节点…...
附录2-tensorflow目标检测
源码来自作者Bubbliiiing,我对参考链接的代码略有修改,网盘地址 链接:百度网盘 请输入提取码 提取码:dvb1 目录 1 参考链接 2 环境 3 数据集准备 3.1 VOCdevkit/VOC2007 3.2 model_data/voc_classes.txt 3.3 voc_an…...

常见的EMC问题
电磁兼容设计的目的就在于满足产品功能要求、减少调试时间,使产品满足电磁兼容标准的要求,并且使产品不会对系统中的其它设备产生电磁干扰。 电磁兼容设计中常见的问题有哪些? 1、电磁兼容设计可以从电路设计(包括器件选择&…...

Redis内存存储效率问题
目录 内存碎片是如何形成的? 如何判断是否有内存碎片? 如何清理内存碎片? INFO命令 面向 Prometheus 的 Redis-exporter 监控 实习期间,了解到,企业级开发中多个项目使用Redis,运行Redis实例的有可能是…...
3.28 haas506 2.0开发教程-example-蓝牙多设备扫描(仅支持M320,HD1)
haas506 2.0开发教程-example-蓝牙多设备扫描案例说明蓝牙信息克隆1.手机蓝牙改名信息克隆代码测试案例说明 开发板扫描蓝牙设备,获取并打印蓝牙设备mac地址。mac地址每个设备不同,且不能更改。本案例仅适用于M320开发板和HD1-RTU。案例使用手机与iBeac…...
C语言经典编程题100例(41~60)
目录41、习题4-4 特殊a串数列求和42、习题4-6 水仙花数43、习题4-7 最大公约数和最小公倍数44、习题7-5 找鞍点45、练习5-1 求m到n之和46、练习5-2 找两个数中最大者47、练习5-3 数字金字塔48、习题5-1 符号函数49、习题5-2 使用函数求奇数和50、习题5-3 使用函数计算两点间的距…...
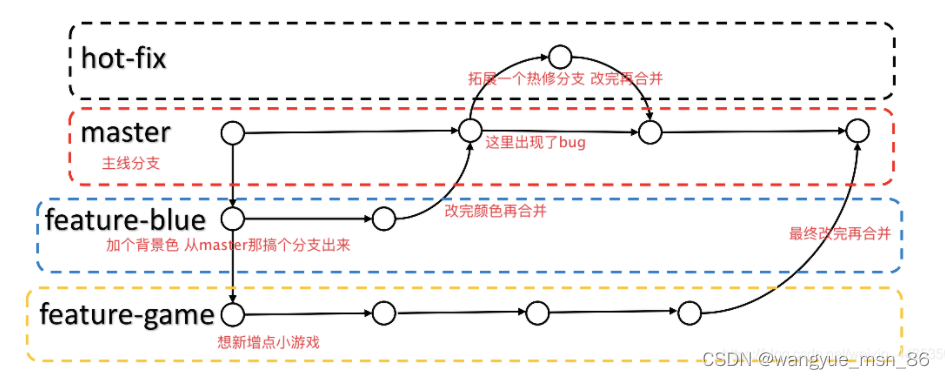
git日常使用命令
实习这段时间使用了很多git指令来提交代码,简单记录一下日常使用的指令: 提交代码通常顺序: 1.git status 查看本地修改项 2.git add . 提交全部文件 (这个 .是全部文件)到暂存区 3.git commit -m ‘本次提交的说明’…...

ES6对象展开运算符浅拷贝or深拷贝
ES6中提出的对象展开运算符“…”就是用来展开元素的。有了它就不用代码循环遍历了,偷懒专用。 1. 合并数组 展开原有数组中的所有元素,可以合并成一个新的数组。 var a[1,2,3]; var b[4,5,6]; var c[...a,...b]; console.log(c) // 输出:…...

leaflet 上传包含shp的zip文件,在map上解析显示图形(059)
第059个 点击查看专栏目录 本示例的目的是介绍演示如何在vue+leaflet中本地上传包含shp的zip文件,利用shapefile读取shp数据,并在地图上显示图形。 直接复制下面的 vue+openlayers源代码,操作2分钟即可运行实现效果 文章目录 示例效果加载shapefile.js方式安装引用jszip(…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...
