机器学习实战:Python基于Logistic逻辑回归进行分类预测
目录
- 1 前言
- 1.1 Logistic回归的介绍
- 1.2 Logistic回归的应用
- 2 iris数据集数据处理
- 2.1 导入函数
- 2.2 导入数据
- 2.3 简单数据查看
- 3 可视化
- 3.1 条形图/散点图
- 3.2 箱线图
- 3.3 三维散点图
- 4 建模预测
- 4.1 二分类预测
- 4.2 多分类预测
- 5 讨论
1 前言
1.1 Logistic回归的介绍
逻辑回归(Logistic regression,简称LR)是一种经典的二分类算法,它将输入特征与一个sigmoid函数进行线性组合,从而预测输出标签的概率。该算法常被用于预测离散的二元结果,例如是/否、真/假等。
优点:
-
实现简单。Logistic回归的参数可以用极大似然估计法进行求解,算法本身非常简单。
-
速度快。Logistic回归计算量小,训练速度快。
-
输出结果易于理解。Logistic回归的输出结果是概率,易于解释。
-
容易扩展。Logistic回归可用于多分类问题和不平衡数据集。
缺点:
-
只适用于线性可分的问题。当特征之间存在非线性关系时,Logistic回归的效果会受到限制。
-
对异常值敏感。由于Logistic回归使用了sigmoid函数,对于异常值非常敏感。
-
容易欠拟合。当特征与目标变量之间的关系非常复杂时,Logistic回归很容易出现欠拟合现象。
1.2 Logistic回归的应用
Logistic回归广泛应用于许多领域,包括:
-
金融风险评估。银行和信用卡公司使用Logistic回归来评估借款人的信用风险,预测贷款违约的概率。
-
医学诊断。Logistic回归可以用于预测患者是否患有某种疾病或病情的严重程度。
-
市场分析。Logistic回归可以用于预测产品或服务的市场需求,并帮助企业做出更好的决策。
-
自然语言处理。Logistic回归可以用于文本分类,例如判断一段文本是否属于某个主题或情感极性。
-
图像处理。Logistic回归可以用于图像分类和目标检测,例如识别数字和字母。
总之,Logistic回归是一种灵活的算法,可以应用于许多不同的领域和问题,特别是在需要预测二元结果的场景中表现出色。
2 iris数据集数据处理
iris数据集共有150个样本,目标变量为花的类别其都属于鸢尾属下的三个亚属(target),分别是山鸢尾 (Iris-setosa),变色鸢尾(Iris-versicolor)和维吉尼亚鸢尾(Iris-virginica)。
四个特征,分别是花萼长度(sepal length)、花萼宽度(sepal width)、花瓣长度(petal length)、花瓣宽度(petal width)。
2.1 导入函数
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
2.2 导入数据
from sklearn.datasets import load_iris
data = load_iris()
iris_target = data.target
iris_features = pd.DataFrame(data=data.data, columns=data.feature_names) #利用Pandas转化为DataFrame格式
2.3 简单数据查看
## 查看数据的整体信息
iris_features.info()## 查看每个类别数量
pd.Series(iris_target).value_counts()
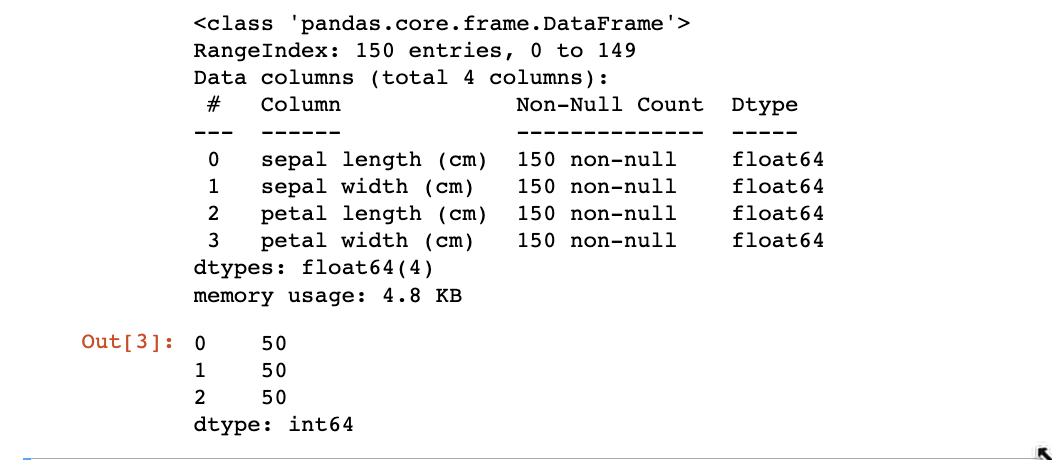
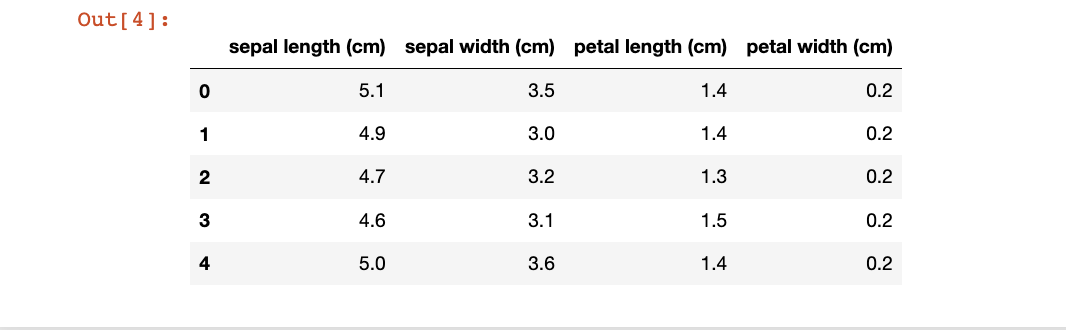
## 查看head或tail
iris_features.head()
#iris_features.tail()
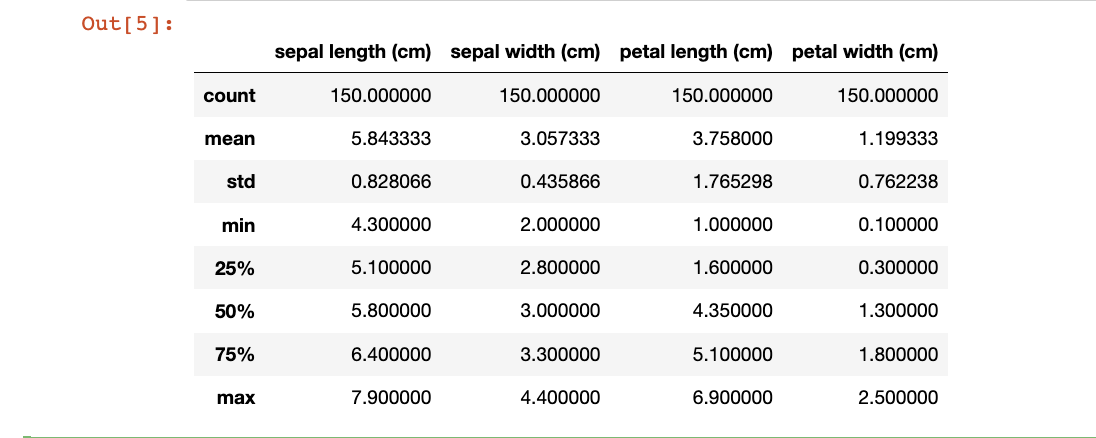
## 对于特征进行一些统计描述
iris_features.describe()
3 可视化
3.1 条形图/散点图
## 合并标签和特征信息
iris_all = iris_features.copy() ##进行浅拷贝,防止对于原始数据的修改
iris_all['target'] = iris_target## 可视化
sns.pairplot(data=iris_all,diag_kind='hist', hue= 'target')
plt.show()
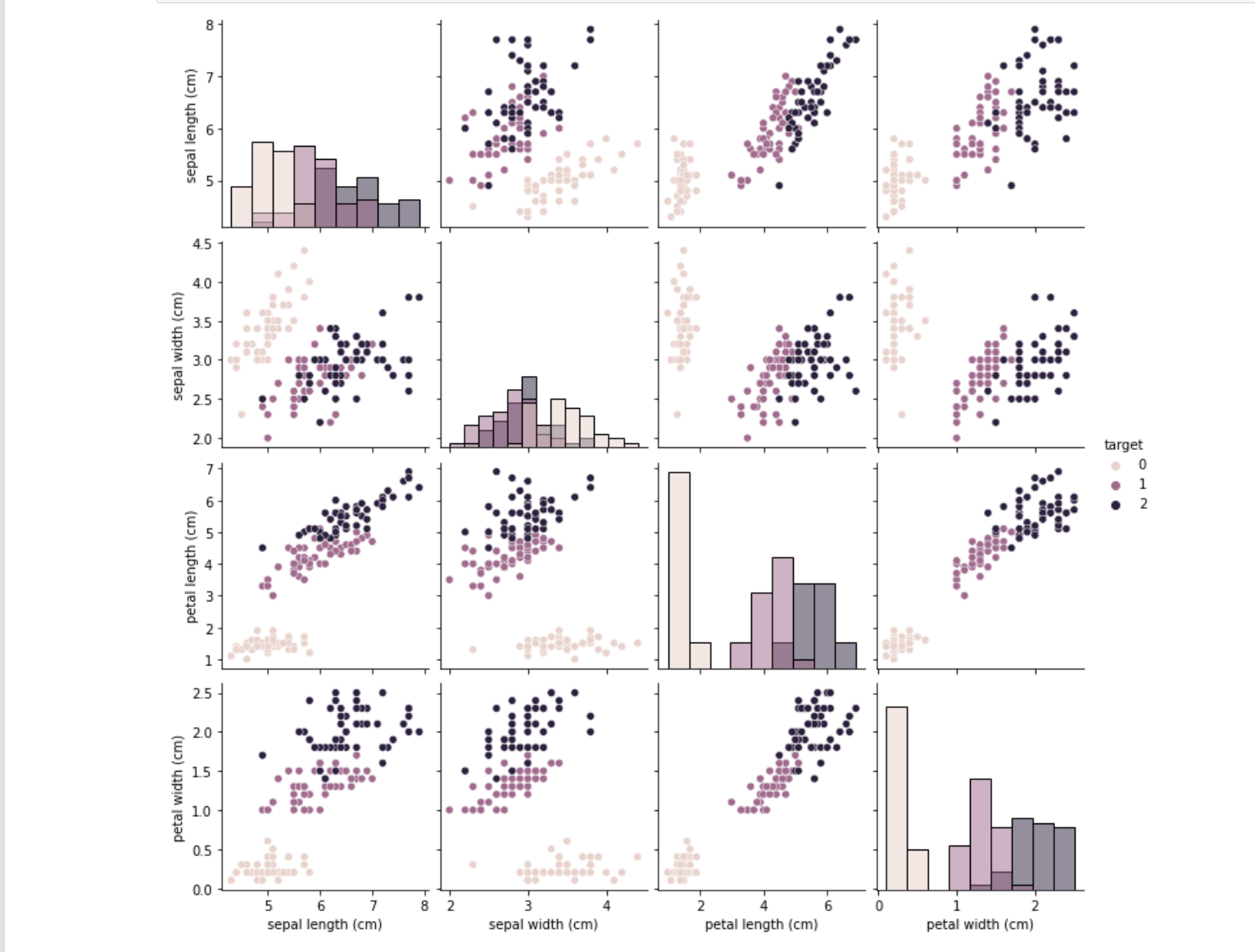
从结果可以发现,在2D情况下不同的特征组合对于不同类别的花的散点分布,以及大概的区分能力。
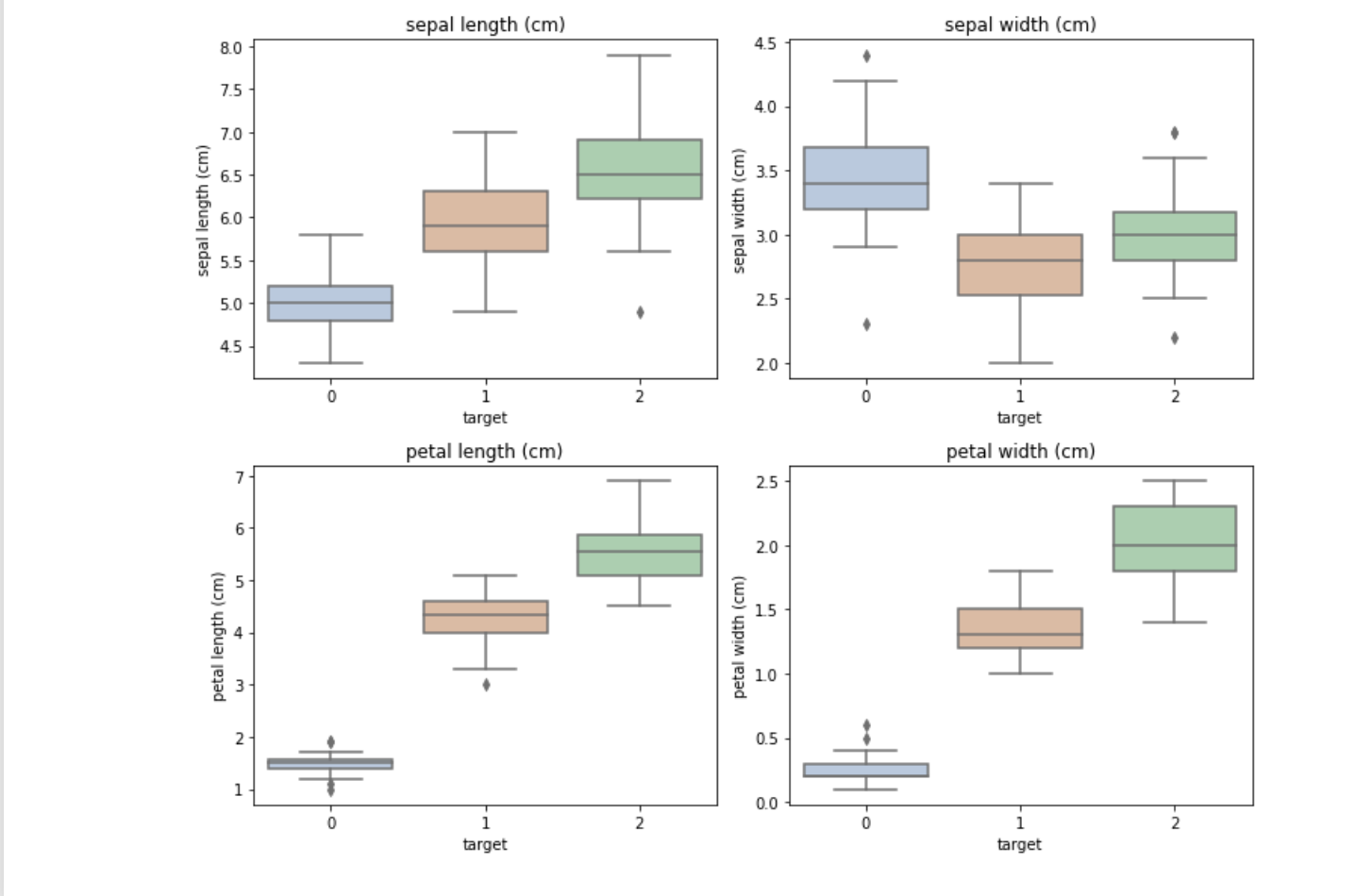
3.2 箱线图
## 构建画布2x2
import matplotlib.pyplot as plt
fig, axes = plt.subplots(nrows=2, ncols=2, figsize=(10, 8))## 可视化
for i, col in enumerate(iris_features.columns):sns.boxplot(ax=axes[i//2, i%2], x='target', y=col, saturation=0.5, palette='pastel', data=iris_all)axes[i//2, i%2].set_title(col)plt.tight_layout()
plt.show()
3.3 三维散点图
from mpl_toolkits.mplot3d import Axes3Dfig = plt.figure(figsize=(10,8))
ax = fig.add_subplot(111, projection='3d')iris_all_class0 = iris_all[iris_all['target']==0].values
iris_all_class1 = iris_all[iris_all['target']==1].values
iris_all_class2 = iris_all[iris_all['target']==2].values
# 'setosa'(0), 'versicolor'(1), 'virginica'(2)
ax.scatter(iris_all_class0[:,0], iris_all_class0[:,1], iris_all_class0[:,2],label='setosa')
ax.scatter(iris_all_class1[:,0], iris_all_class1[:,1], iris_all_class1[:,2],label='versicolor')
ax.scatter(iris_all_class2[:,0], iris_all_class2[:,1], iris_all_class2[:,2],label='virginica')
plt.legend()plt.show()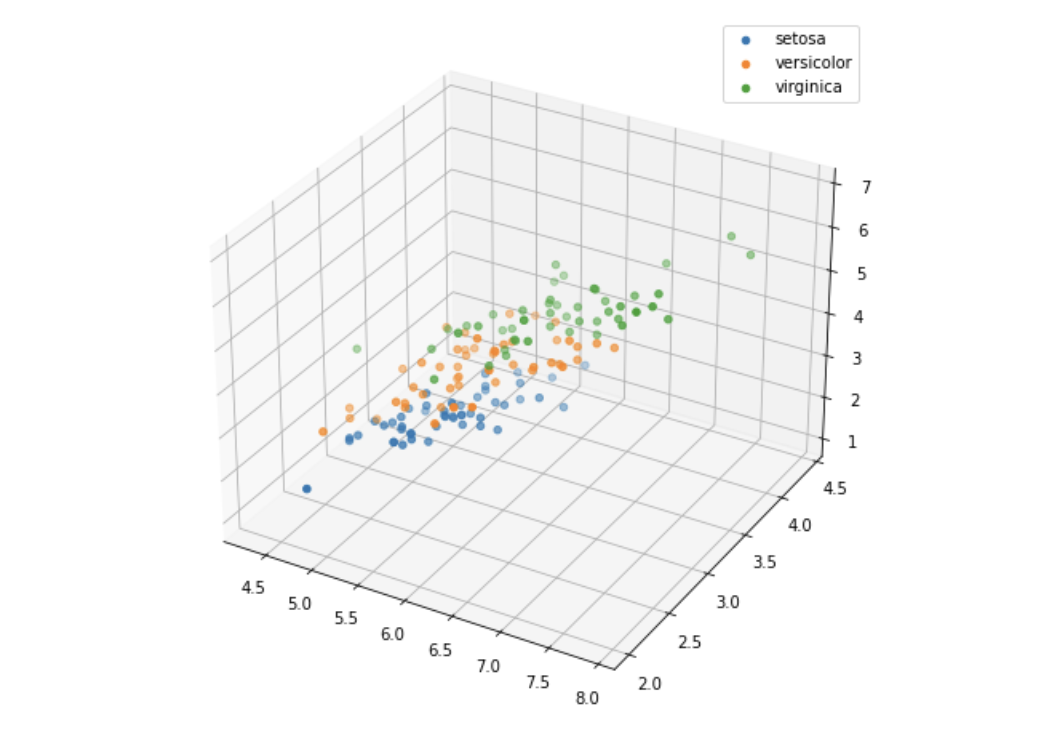
4 建模预测
4.1 二分类预测
## 划分为训练集和测试集
from sklearn.model_selection import train_test_split## 选择其类别为0和1的样本 (不包括类别为2的样本)
iris_features_part = iris_features.iloc[:100]
iris_target_part = iris_target[:100]## 训练集测试集7/3分
x_train, x_test, y_train, y_test = train_test_split(iris_features_part, iris_target_part, test_size = 0.3, random_state = 2020)## 从sklearn中导入逻辑回归模型
from sklearn.linear_model import LogisticRegression
clf = LogisticRegression(random_state=0, solver='lbfgs')# 训练模型
clf.fit(x_train, y_train)
## 查看其对应的w
print('the weight of Logistic Regression:',clf.coef_)## 查看其对应的w0
print('the intercept(w0) of Logistic Regression:',clf.intercept_)

## 预测模型
train_predict = clf.predict(x_train)
test_predict = clf.predict(x_test)
from sklearn import metrics## 利用accuracy(准确度)评估模型效果
print('The accuracy of the Logistic Regression is:',metrics.accuracy_score(y_train,train_predict))
print('The accuracy of the Logistic Regression is:',metrics.accuracy_score(y_test,test_predict))## 查看混淆矩阵 (预测值和真实值的各类情况统计矩阵)
confusion_matrix_result = metrics.confusion_matrix(test_predict,y_test)
print('The confusion matrix result:\n',confusion_matrix_result)# 可视化
plt.figure(figsize=(8, 6))
sns.heatmap(confusion_matrix_result, annot=True, cmap='Blues')
plt.xlabel('Predicted labels')
plt.ylabel('True labels')
plt.show()
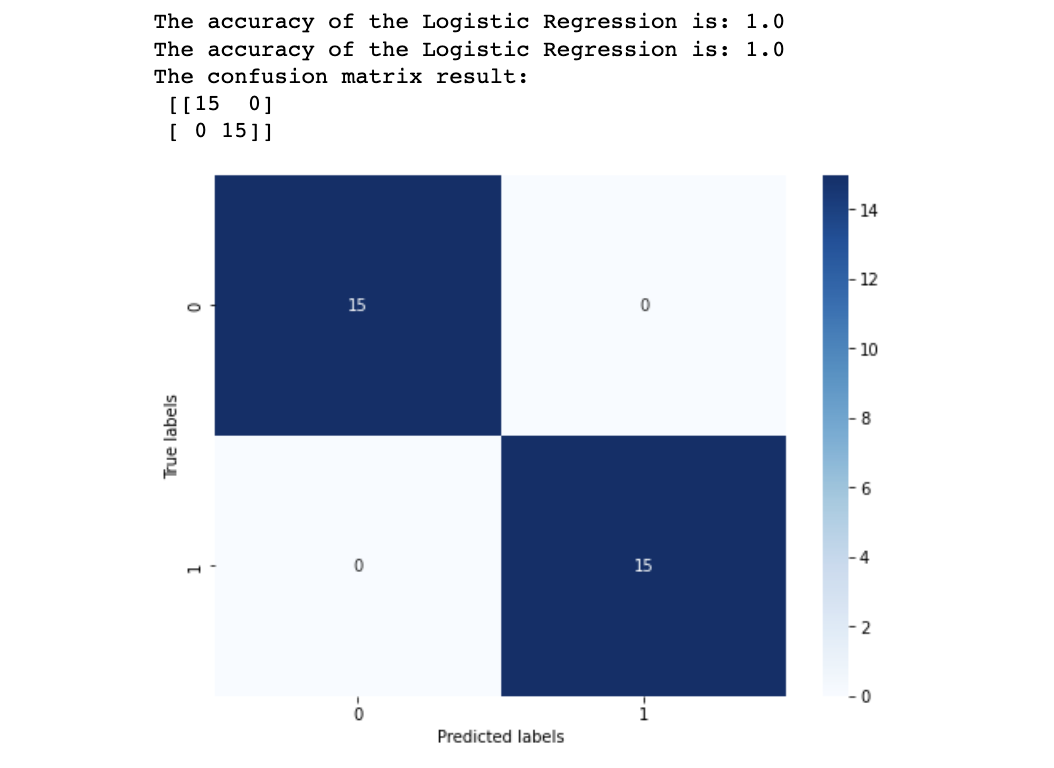
结果准确度为1,代表所有的样本都预测正确了,绝杀
4.2 多分类预测
## 训练集测试集还是7/3分
x_train, x_test, y_train, y_test = train_test_split(iris_features, iris_target, test_size = 0.3, random_state = 2020)## 建模
clf = LogisticRegression(random_state=0, solver='lbfgs')## 训练模型
clf.fit(x_train, y_train)

## 预测模型
train_predict = clf.predict(x_train)
test_predict = clf.predict(x_test)## p = p(y=1|x,\theta)),预测模型概率
train_predict_proba = clf.predict_proba(x_train)
test_predict_proba = clf.predict_proba(x_test)print('The test predict Probability of each class:\n',test_predict_proba)
## 其中第一列代表预测为0类的概率,第二列代表预测为1类的概率,第三列代表预测为2类的概率。## 利用accuracy评估模型效果
print('The accuracy of the Logistic Regression is:',metrics.accuracy_score(y_train,train_predict))
print('The accuracy of the Logistic Regression is:',metrics.accuracy_score(y_test,test_predict))

比起二分类的1略小,但均大于0.9
## 查看混淆矩阵
confusion_matrix_result = metrics.confusion_matrix(test_predict,y_test)
print('The confusion matrix result:\n',confusion_matrix_result)# 可视化
plt.figure(figsize=(8, 6))
sns.heatmap(confusion_matrix_result, annot=True, cmap='Blues')
plt.xlabel('Predicted labels')
plt.ylabel('True labels')
plt.show()
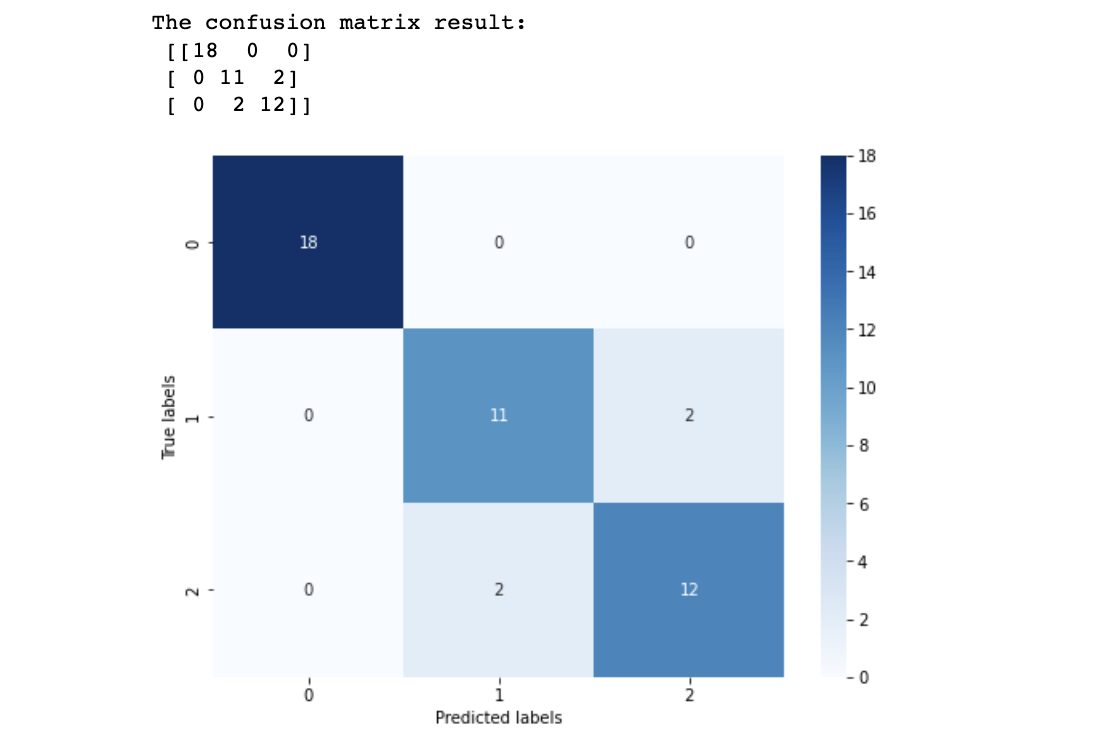
根据结果发现,其在三分类的结果的预测准确度上有所下降,但好在测试集还有91%,这是由于versicolor(1)和 virginica(2)这两个类别的特征,我们从可视化的时候也可以发现,其特征的边界具有一定的模糊性(边界类别混杂,没有明显区分边界),所有在这两类的预测上出现了一定的错误。
5 讨论
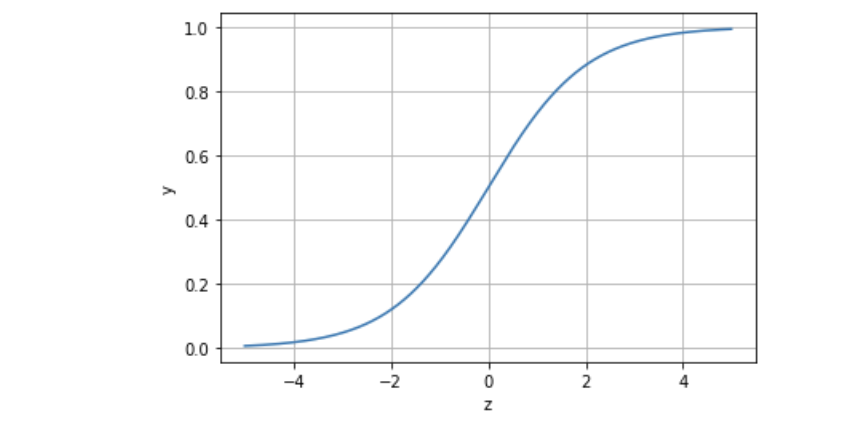
Logistic回归虽然名字里带“回归”,但是它实际上是一种分类方法,主要用于两分类问题(即输出只有两种,分别代表两个类别),所以利用了Logistic函数(或称为Sigmoid函数)
原理的简单解释:当z=>0时, y=>0.5,分类为1,当z<0时, y<0.5,分类为0,其对应的y值我们可以视为类别1的概率预测值,而多分类其实就是将多个二分类的逻辑回归组合。
相关文章:

机器学习实战:Python基于Logistic逻辑回归进行分类预测
目录1 前言1.1 Logistic回归的介绍1.2 Logistic回归的应用2 iris数据集数据处理2.1 导入函数2.2 导入数据2.3 简单数据查看3 可视化3.1 条形图/散点图3.2 箱线图3.3 三维散点图4 建模预测4.1 二分类预测4.2 多分类预测5 讨论1 前言 1.1 Logistic回归的介绍 逻辑回归ÿ…...
Leetcode.404 左叶子之和
题目链接 Leetcode.404 左叶子之和 easy 题目描述 给定二叉树的根节点 root,返回所有 左叶子 之和。 示例 1: 输入: root [3,9,20,null,null,15,7] 输出: 24 解释: 在这个二叉树中,有两个左叶子,分别是 9 和 15,所以…...

Android 11.0 原生SystemUI下拉通知栏UI背景设置为圆角背景的定制(二)
1.前言 在11.0的系统rom定制化开发中,在原生系统SystemUI下拉状态栏的下拉通知栏的背景默认是白色四角的背景, 由于在产品设计中,在对下拉通知栏通知的背景需要把四角背景默认改成圆角背景,所以就需要分析系统原生下拉通知栏的每条通知的默认背景, 然后通过systemui的通知…...

C语言CRC-16 IBM格式校验函数
C语言CRC-16 IBM格式校验函数 CRC-16校验产生2个字节长度的数据校验码,通过计算得到的校验码和获得的校验码比较,用于验证获得的数据的正确性。基本的CRC-16校验算法实现,参考: C语言标准CRC-16校验函数。 不同厂家通过对输入数…...
Maven高级-聚合和继承
Maven高级-聚合和继承3,聚合和继承3.1 聚合步骤1:创建一个空的maven项目步骤2:将项目的打包方式改为pom步骤3:pom.xml添加所要管理的项目步骤4:使用聚合统一管理项目3.2 继承步骤1:创建一个空的Maven项目并将其打包方式设置为pom步骤2:在子项目中设置其父工程步骤3:…...

如何写出10万+ Facebook 贴文?
想要创作一篇优秀的Facebook贴文,首先要考虑以下几个问题: 1.文案特点 一篇清晰简洁的文案有助于受众在有限的浏览时间内快速了解你想要展示的信息。根据以往经验,文案内容最好保持在20个汉字以内,加上链接描述最好也不要超过50…...

图像处理数据集
BSDS500 Berkeley Segmentation Dataset 500 是第一个用于评估超像素算法的数据集。对于参数优化,使用了验证集。 500张数据集200训练集train100验证集val200测试集test 每张图像有 5 个不同的高质量地面真值分割(groundTruth,是.mat文件) …...
文本聚类与摘要,让AI帮你做个总结
你好,我是徐文浩。 上一讲里,我们用上了最新的ChatGPT的API,注册好了HuggingFace的账号,也把我们的聊天机器人部署了出去。希望通过这个过程,你对实际的应用开发过程已经有了充足的体验。那么这一讲里,我们…...
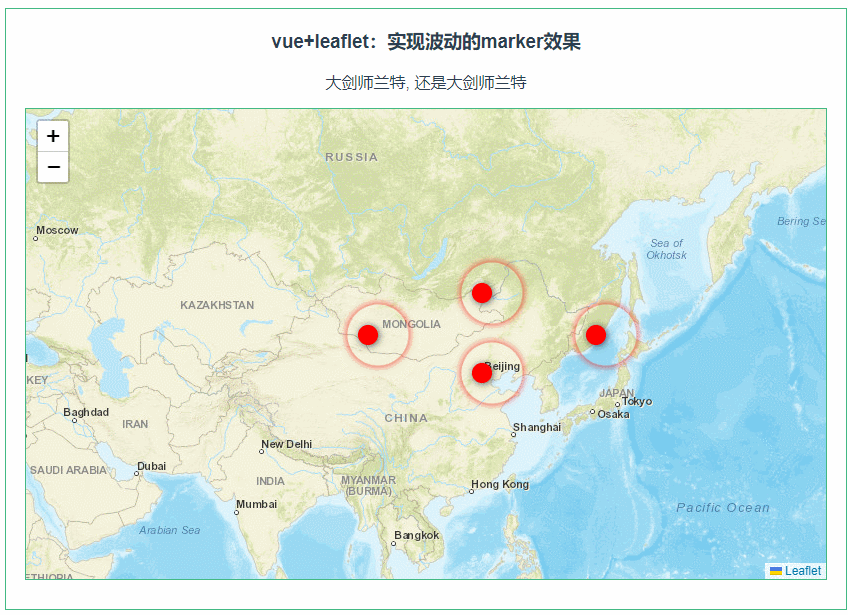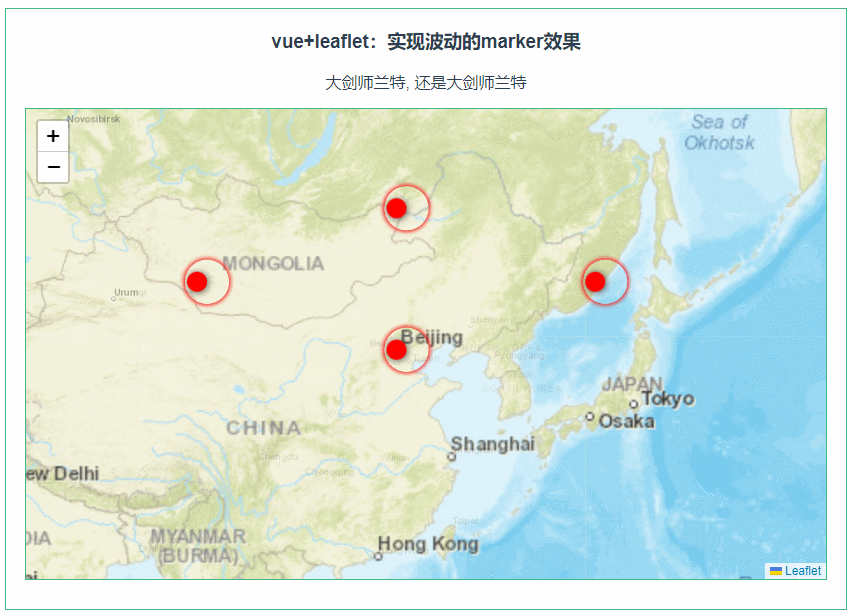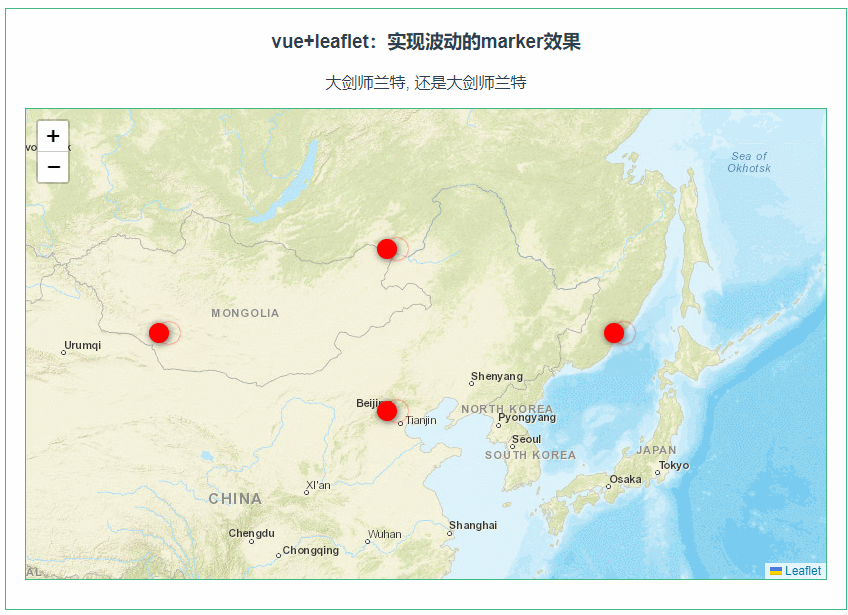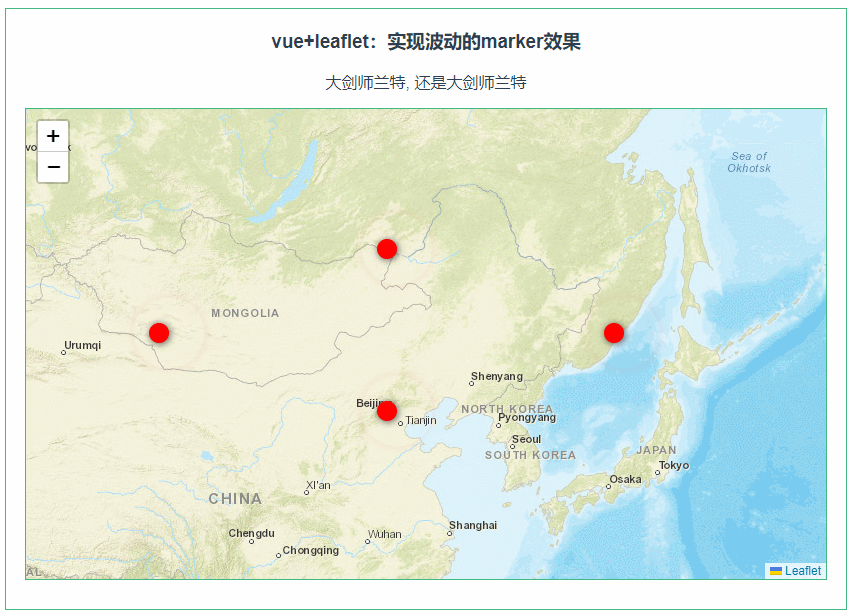
leaflet实现波动的marker效果(131)
第131个 点击查看专栏目录 本示例的目的是介绍如何在vue+leaflet中显示波动的marker效果。 直接复制下面的 vue+leaflet源代码,操作2分钟即可运行实现效果. 文章目录 示例效果配置方式示例源代码(共76行)安装插件相关API参考:专栏目标示例效果 配置方式 1)查看基础设置…...

关于Dataset和DataLoader的概念
关于Dataset和DataLoader的概念 在机器学习中,Dataset和DataLoader是两个很重要的概念,它们通常用于训练和测试模型时的数据处理。 Dataset是指用于存储和管理数据的类。在深度学习中,通常将数据存储在Dataset中,并使用Dataset提…...

前端与JS变量
前端开发是当今互联网发展的重要组成部分,而JavaScript变量则是前端开发中不可或缺的一部分。在前端开发中,变量的作用不仅仅是存储数据,还可以用来控制程序流程、实现动态效果等。因此,学习前端与JavaScript变量是非常必要的。 …...
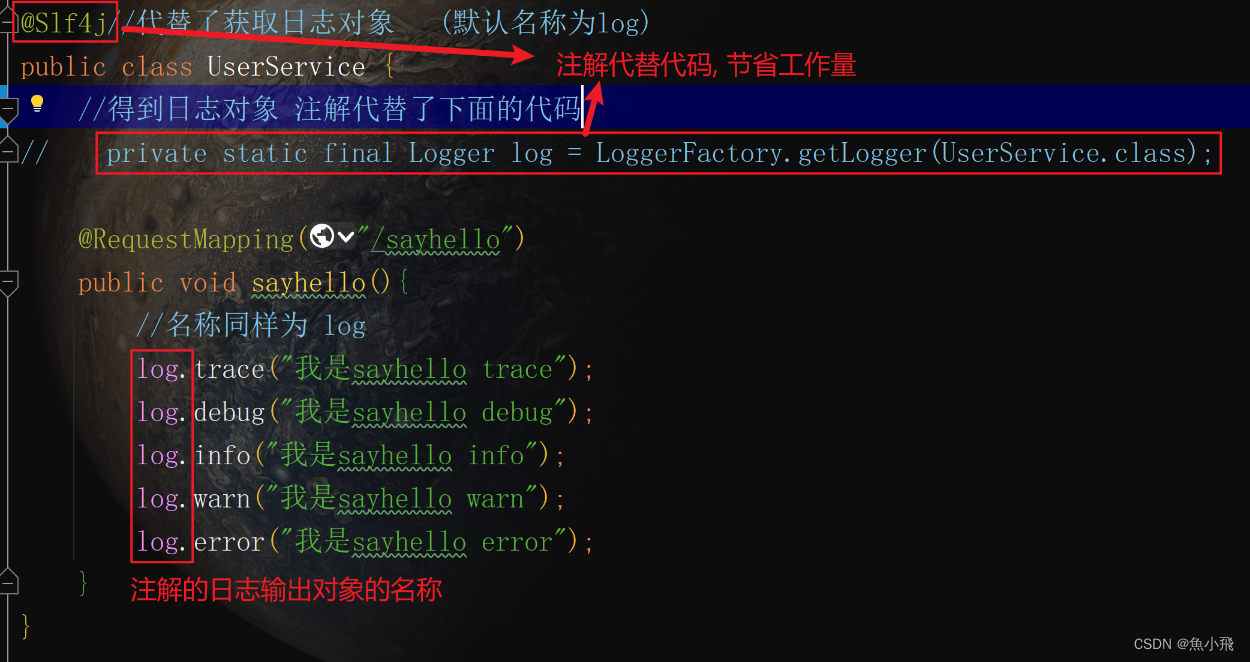
初始SpringBoot
初始SpringBoot1. SpringBoot创建和运行1.1. SpringBoot的概念1.2. SpringBoot的优点1.3. SpringBoot的创建1.3.0. 前置工作:安装插件(这是社区版需要做的工作, 专业版可以忽略)1.3.1. 社区版创建方式1.3.2. 专业版创建方式1.3.3. 网页版创建方式1.4. 项目目录介绍1.5. SpringB…...
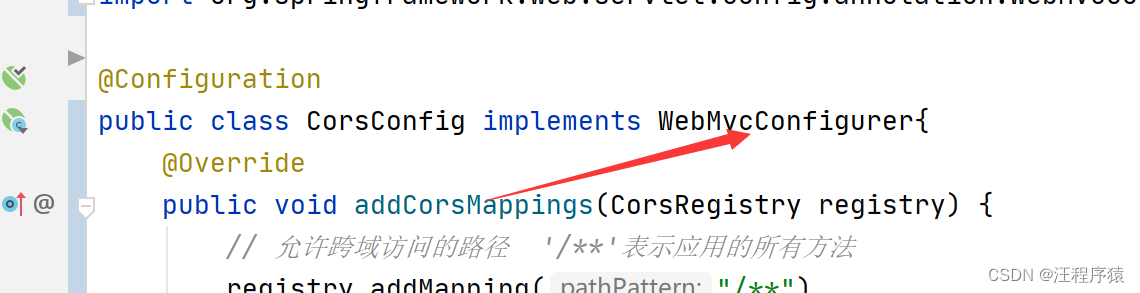
vue+springboot 上传文件、图片、视频,回显到前端。
效果图 预览: 视频: 设计逻辑 数据库表 前端vue html <div class"right-pannel"><div class"data-box"><!--上传的作业--><div style"display: block" id""><div class"tit…...
)
java入门-W3(K81-K143)
一. 什么是对象 什么是对象?之前我们讲过,对象就是计算机中的虚拟物体。例如 System.out,System.in 等等。然而,要开发自己的应用程序,只有这些现成的对象还远远不够。需要我们自己来创建新的对象。 例如,…...

English Learning - L2 语音作业打卡 复习元音 [ɜː] [æ] 辅元连读技巧 Day42 2023.4.3 周一
English Learning - L2 语音作业打卡 复习元音 [ɜː] [] 辅元连读技巧 Day42 2023.4.3 周一💌发音小贴士:💌当日目标音发音规则/技巧:中元音 [ɜː]前元音 []辅元连读技巧🍭 Part 1【热身练习】🍭 Part2【练习内容】&…...

Thinkphp 6.0图像处理功能
本节课我们来学习一下图像处理功能,这功能是外置的,并非系统内置。 一.图像处理功能 1. 图像处理功能不是系统内置的功能了,需要通过 composer 引入进来; composer require topthink/think-image 2. 引入进来之后&…...

表格软件界的卷王,Excel、access、foxpro全靠边,WPS:真荣幸
Excel和Access就是表格软件的选择? 现在,铺天盖地的Excel的技能教程可谓是满天飞,有网上的教程,也有视频直播课程。 很多办公人员用Excel这种表格软件与VBA结合,甚至用不遗余力去学习Python编程语法,但Exce…...
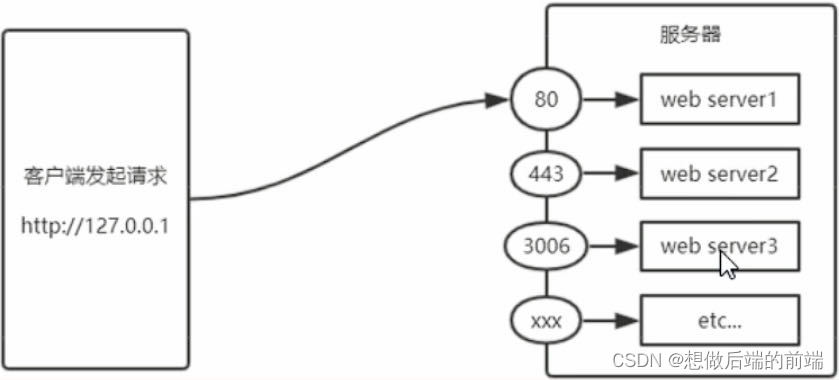
Node.js -- http模块
1. 什么是http模块 在网络节点中,负责消费资源的电脑,叫客户端;负责对外提供网络资源的电脑,叫做服务器。 http模块是Node.js官方提供的,用来创建web服务器的模块。通过http模块提供的http.createServer()方法&#…...
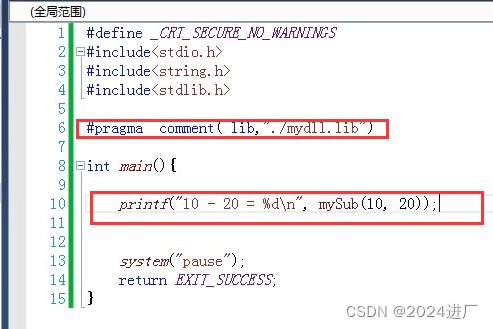
静态库与动态库
库是已经写好的、成熟的、可复用的代码。在我们的开发的应用中经常有一些公共代码是需要反复使用的,就把这些代码编译为库文件。库可以简单看成一组目标文件的集合,将这些目标文件经过压缩打包之后形成的一个可执行代码的二进制文件。库有两种࿱…...

问题 A: C语言11.1
题目描述: 完成一个对候选人得票的统计程序。假设有3个候选人,名字分别为Li,Zhang和Fun。使用结构体存储每一个候选人的名字和得票数。记录每一张选票的得票人名,输出每个候选人最终的得票数。结构体可以定义成如下的格式&#x…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

MySQL 主从同步异常处理
阅读原文:https://www.xiaozaoshu.top/articles/mysql-m-s-update-pk MySQL 做双主,遇到的这个错误: Could not execute Update_rows event on table ... Error_code: 1032是 MySQL 主从复制时的经典错误之一,通常表示ÿ…...

webpack面试题
面试题:webpack介绍和简单使用 一、webpack(模块化打包工具)1. webpack是把项目当作一个整体,通过给定的一个主文件,webpack将从这个主文件开始找到你项目当中的所有依赖文件,使用loaders来处理它们&#x…...

归并排序:分治思想的高效排序
目录 基本原理 流程图解 实现方法 递归实现 非递归实现 演示过程 时间复杂度 基本原理 归并排序(Merge Sort)是一种基于分治思想的排序算法,由约翰冯诺伊曼在1945年提出。其核心思想包括: 分割(Divide):将待排序数组递归地分成两个子…...

Linux-进程间的通信
1、IPC: Inter Process Communication(进程间通信): 由于每个进程在操作系统中有独立的地址空间,它们不能像线程那样直接访问彼此的内存,所以必须通过某种方式进行通信。 常见的 IPC 方式包括&#…...
